抛掷爆破混凝土介质飞散行为研究

肖建光， 郑元枫， 余庆波， 王海福

(北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)



抛掷爆破混凝土介质飞散行为研究

肖建光， 郑元枫， 余庆波， 王海福

(北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)

针对内爆炸载荷作用下混凝土介质的抛掷问题，采用量纲分析与数值模拟相结合的方法，对抛掷爆破条件下混凝土介质飞散行为进行了研究. 通过量纲分析得到了以装药量与埋深为自变量的关于平均抛掷速度的函数表达式. 基于爆坑内混凝土介质抛掷速度的分布规律，定义了爆破后混凝土介质的平均抛掷速度. 基于AUTODYN-2D数值模拟结果数据，拟合得到了用于估算平均抛掷速度的工程表达式. 为了验证该公式的适用性，对其进行了显著性检验，结果表明，该公式在置信水平为0.99条件下是显著的，说明其精度较高，具有较好的适用性.

抛掷爆破；平均抛掷速度；量纲分析；光滑粒子流体动力学(SPH)

深钻地掘进武器系统概念及技术的发展，为有效打击地下深层坚固目标提供了新途径. 深钻地掘进弹对目标的打击和毁伤过程可分为两个阶段：掘进开坑过程，通过弹载多管火炮系统齐射多枚侵爆子弹，利用侵爆子弹的侵彻/爆破作用，将地下岩土抛掷至地面以上，形成一个用于投放主战斗部的井道；主战斗部随进和摧毁目标过程，主战斗部爆炸后产生强烈的冲击波与大量高温高压爆轰产物对深埋地下的指挥人员与设备进行致命打击[1].

掘进开坑是影响深钻地掘进武器打击深度的决定性因素，也是深钻地掘进武器的核心技术. 其本质是侵爆子弹侵彻/爆破后形成破碎岩土的抛掷飞散问题，因此开展内爆炸载荷作用下混凝土介质成坑过程及飞散行为具有重要的理论与现实意义. 然而，近年来国内外学者对爆炸载荷作用下混凝土动态响应问题的研究主要着眼于混凝土力学行为与弹坑尺寸[2-5]，而关于混凝土介质破碎后抛掷问题的研究则较少. 此外，对于侵爆子弹参数化设计而言，实验研究可以形成较为系统、接近实际的数据库，然而实验所消耗的人力、物力与财力都相当大. 本文采用量纲分析与数值模拟相结合的方法，对被爆破介质飞散行为的影响因素进行了研究，拟合得到了用于估算混凝土爆破抛掷速度的半经验公式，可为侵爆子弹参数化设计提供指导和参考.

1 理论分析

1.1 量纲分析

抛掷速度与漏斗坑底圆半径是装药在混凝土中爆破的两个重要的威力效应参量，与爆破效应威力参量有关相互独立的控制参量8个，威力参量1个，共9个. 在力学问题中，基本独立参量为3个，取W，ρmo，σt为3个基本独立参量，其余7个量经量纲一化整理，如表1所示.

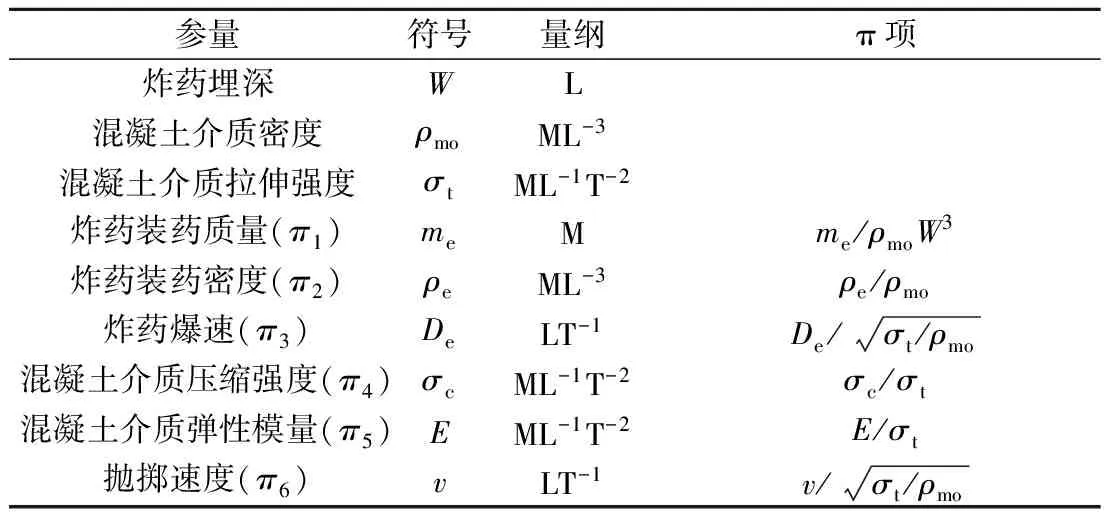
表1 爆破参量量纲

爆破效应威力参量v分别是炸药、混凝土介质的相互独立的8个控制参量的函数：

(1)

根据π定理，并将π1进行变换：

(2)

(3)

为简化式(3)，假设装药密度、爆速、混凝土介质密度、压缩强度、拉伸强度、弹性模量等6个参量均为不变量，则π1，π3，π4，π5均为常量. 对于某种介质，材料参数σt与ρmo为定值，则

(4)

1.2 爆破弹坑碎片平均抛掷速度

在抛掷爆破中，漏斗形弹坑内混凝土介质速度各不相同. 如图1所示，ΔOAW表示被抛掷的混凝土介质，考虑到漏斗形爆坑的对称性，平均速度为

(5)

文献[6]对WA方向上混凝土介质抛掷速度分布进行了研究，结果表明在WA方向上抛掷速度服从指数分布，其分布型态为

(6)

式中：x为WA方向上任一点与预制孔孔口之间的距离；vmax为最大抛掷速度，即是W点抛掷速度；β为混凝土介质抛掷速度分布系数.

在OM方向上，假设速度不变，则

(7)

式中：vM为ΔOAW内任意一点的速度；vx为OM与WA交点的速度.

作为关照，程瀚也获得了价值不菲的回报。从2012年开始，程瀚陆续向仰某“借”手表，先后“借”其6块手表和一块翡翠。而其中有一块价值达1300万港币的瑞士“百达翡丽”5002P手表更是让程瀚“垂涎三尺”。当时程瀚说让仰某把这块表放在安全的地方，保证他以后想玩这块表的时候，随时能拿出来。仰某就把这块“百达翡丽”表放在合肥家中的保险柜里。

将式(6)(7)代入式(5)得

(8)

2 混凝土介质飞散行为数值模拟

2.1 计算模型

采用SPH方法对炸药在混凝土中爆破过程进行数值模拟，混凝土靶板为圆柱体，靶板上方留有用于放置药柱的预制孔. 装药质量分别为22，176，1 408 g，壳体厚度为2 mm. 为了便于计算，数值计算时建立二维轴对称模型，计算模型如图2所示.

本文采用JWL状态方程描述炸药材料产生化学能的释放过程. RHT模型引入了损伤以及偏应力张量第三不变量，可以较好地描述混凝土介质在内爆载荷作用下的动态响应，近些年来被越来越多的国内外学者所采用. 然而，Autodyn默认的RHT模型参数具有一定的局限性，例如在某种应力条件下材料在失效后会表现出一些硬化现象，与实际情况明显不符. 文献[7]对RHT模型的一些参数进行了改进，并用试验验证了参数的有效性. 表2为本文采用的混凝土介质材料参数.

2.2 数值模拟结果

为了研究介质飞散行为与装药量和埋深之间的关系，本文共做了18次数值模拟，数值模拟方案如表3所示. 按装药量可以分为A，B，C 3种配置，其装药量分别为0.22，0.176，1.408 kg.

图3为A配置不同埋深条件下数值模拟结果，其中药柱质量为22 g. 由图中可以看出，埋深不同，则爆破破片分布不同，当埋深较小时，炸药爆轰能量大部分流向空气中，爆坑体积较小. 此时破片分布锥角较大，抛掷速度较高. 随着埋深的加大，周围介质侧向约束逐步增强，炸药爆轰能量更多的用于破碎与抛掷混凝土介质，破片分布锥角逐渐减小，抛掷速度持续降低. 当埋深进一步加深时，爆破演变为松动爆破，炸药爆炸只能造成装药周围混凝土介质的破碎，而不发生抛掷现象.

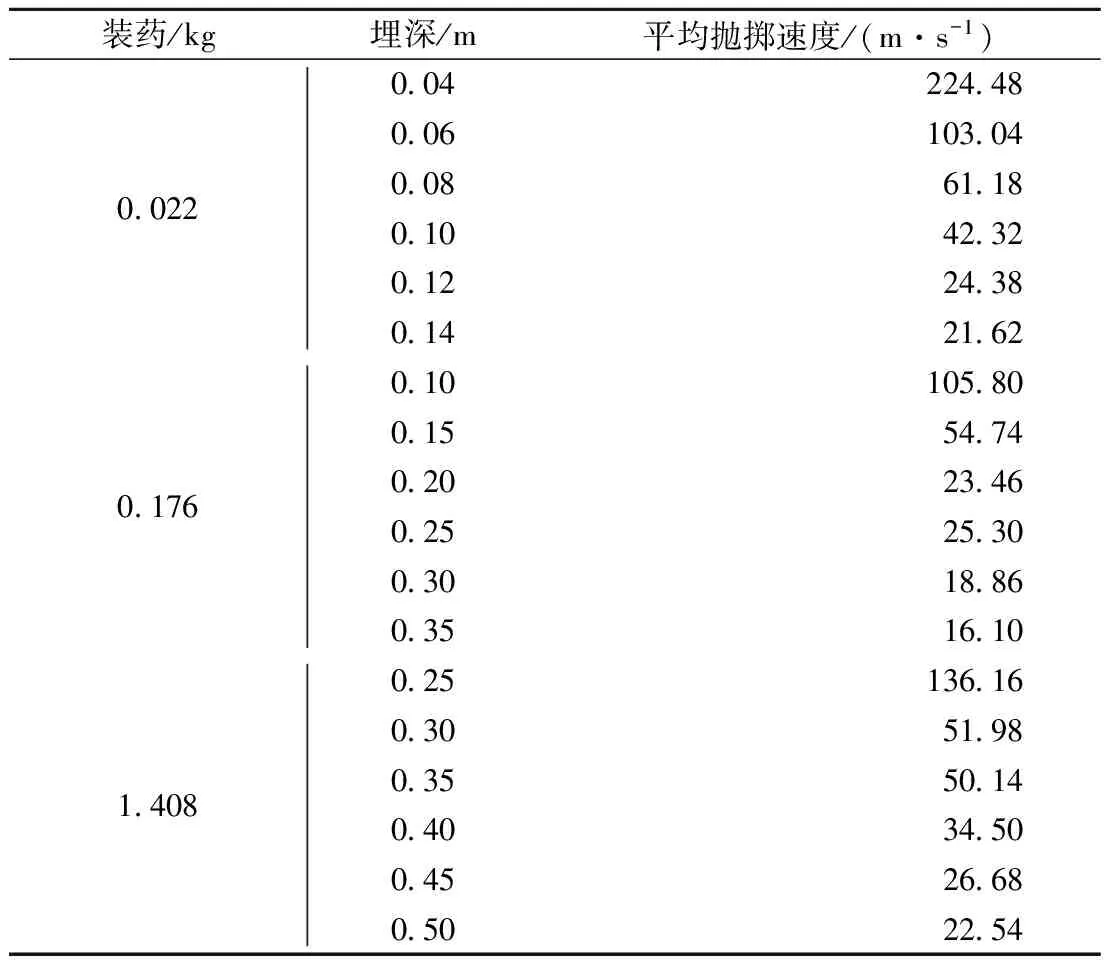
表3 数值模拟结果

此外，混凝土介质抛掷速度随着与预制孔孔口距离的增加而降低，即距离预制孔孔口越近，速度越高，其最大值位于预制孔孔壁与混凝土靶自由面交界处附近.

3 拟合关系式

(9)

为了验证拟合关系式的适用性，需要对其进行精度幂函数相关关系显著性评估. 将式(9)两边取对数，则问题简化为检验线性相关关系的显著性. 本文采用R检验法[8]，即通过相关系数R检验lnvav与ln (m1/3/W)之间的线性关系.

(10)

由显著性水平α=0.01，自由度18-2=16，查相关系数显著性检验表，得临界值R0.01=0.590.

由于R=0.966>0.590=R0.01，故认为lnvav与ln (m1/3/W)之间的线性关系，即vav与m1/3/W幂函数关系特别显著，所得拟合关系式(9)确实能反映vav与m1/3/W之间的幂函数相关关系.

4 结 论

① 分析了混凝土在内爆载荷作用下抛掷速度的影响因素，并对其进行了量纲分析，得到了以装药量与埋深为自变量的关于抛掷速度的函数表达式.

② 基于AUTODYN-2D数值模拟平台，采用光滑粒子流体动力学算法(SPH)对混凝土中不同药量、不同埋深条件下抛掷速度进行了数值模拟. 基于数值模拟结果数据，拟合得到用于估算平均抛掷速度的关系式.

③ 对关于平均抛掷速度的半经验公式进行了相关系数显著性检验，结果表明，该表达式在置信水平为0.99条件下是显著的，说明该公式精度较高，具有较好的适用性.

[1] Burns D. Deep digger weapons system development[C]//Proceedings of the 41st Annual NDIA Gun and Missile Systems Conference. [S.l.]: NDIA, 2006:236-247.

[2] Liu Yan， Duan Zhuoping， Huang Fenglei， et al. Damage effects of shelled explosive explosion in concrete[J]. Defence Science Journal， 2010，60(6):672-677.

[3] Luccioni B， Ambrosini D， Nurick G， et al. Craters produced by underground explosions[J]. Computers & Structures， 2009，87(21):1366-1373.[4] 王静，贾宝华，李伟，等.混凝土材料的动态力学性能研究[J].北京理工大学学报，2013，33(8):776-782.

Wang Jing， Jia Baohua， Li Wei， et al. Mechanical behavior of concrete under dynamic loadings[J]. Transactions of Beijing Institute of Technology， 2013，33(8):776-782. (in Chinese)

[5] 张海英，段卓平，刘彦，等.有限厚混凝土靶内部爆炸震塌贯穿研究[J].北京理工大学学报，2013，33(5):441-444.

Zhang Haiying， Duan Zhuoping， Liu Yan， et al. Study on the collapse perforation of thick concrete targets under internal explosion[J]. Transactions of Beijing Institute of Technology， 2013，33(5):441-444. (in Chinese)

[6] 梁润.抛掷爆破的岩石抛掷速度[J].武汉水利电力学院学报，1980(3)：39-46.

Liang Run. Ejection velocity of rock in cast blasting[J]. Engineering Journal of Wuhan University， 1980(3)：39-46. (in Chinese)

[7] Tu Z， Lu Y. Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations[J]. International Journal of Impact Engineering， 2009，36(1):132-146.

[8] 肖筱南.新编概率论与数理统计[M].北京:北京大学出版社，2013.

Xiao Xiaonan. The new theory of probability and mathematical statistics[M]. Beijing: Peking University Press， 2013. (in Chinese)

(责任编辑：刘雨)

Ejection Behavior of Concrete Materials Under Cast Blasting

XIAO Jian-guang， ZHENG Yuan-feng， YU Qing-bo， WANG Hai-fu

(State Key Laboratory of Explosion Science and Technology， Beijing Institute of Technology， Beijing 100081， China)

The ejection velocity of fragmented concrete mass formed in the cast blasting was studied with the method of dimensional analysis and numerical simulation. The influence factors of casting velocity was analyzed, and function expression of casting velocity with charge mass and depth of burial as independent variable was derived by dimensional analysis. Average ejection velocity was defined according to the distribution of the fragmented concrete mass. Ejection velocity varies from different charge mass and depth of burial was simulated by SPH using AUTODYN-2 code. With the simulation results, the semi-empirical formula for ejection velocity was fitted. The significance testing for the semi-empirical formula was conducted. And the results show that the confidence level is more than 0.99, and the accuracy of this formula fully meet the engineering requirements.

cast blasting; ejection velocity; dimensional analysis; smoothed particle hydrodynamics (SPH)

2015-05-15

肖建光(1984—)，男，博士生，E-mail:3120120087@bit.edu.cn.

王海福(1966—)，男，教授，博士生导师，E-mail:wanghf@bit.edu.cn.

TJ 414

A

1001-0645(2016)10-1015-05

10.15918/j.tbit1001-0645.2016.10.006