基于稀疏谱匹配的高分辨DOA估计方法
陈建, 田野, 孙晓颖
(1.吉林大学 通信工程学院,吉林,长春 130022;2.燕山大学 信息科学与工程学院,河北,秦皇岛 066004)
基于稀疏谱匹配的高分辨DOA估计方法
陈建1, 田野2, 孙晓颖1
(1.吉林大学 通信工程学院,吉林,长春 130022;2.燕山大学 信息科学与工程学院,河北,秦皇岛 066004)
针对迭代加权最小二乘类稀疏重构算法性能易受过完备基条件数影响的缺陷,提出了一种基于稀疏谱匹配的高分辨DOA估计新方法. 对过完备基进行奇异值分解,采用TSVD方法剔除较小奇异值对应的特征向量,获得一个良态矩阵,并用此矩阵替代的过完备基矩阵,采用lp范数约束正则化FOCUSS算法进行稀疏重构,解决了因网络划分过细造成的过完备基条件数过大带来的病态问题,并用粗、细两步网格划分来降低算法的复杂度. 仿真结果表明,相对于MFOCUSS方法,本文方法不仅具有较低的计算复杂度,而且具有更高的分辨率和噪声鲁棒性.
DOA;稀疏重构;过完备基;FOCUSS;奇异值分解
高分辨波达方向(direction of arrival, DOA)估计是阵列信号处理领域的主要研究内容之一. 自20世纪60年代以来,为了克服传统波束成形方法难以突破瑞利限的限制,学者们提出了大量有效的高分辨DOA估计方法,以CAPON方法、MUSIC和ESPRIT为代表[1].
近年来,随着压缩感知理论体系[2]的出现和不断完善,作为其核心理论的稀疏信号重构引起了国内外学者的广泛关注,并已广泛应用于雷达、无线传感器网络、图像处理、生物传感、光谱分析以及信道均衡等领域[3],针对这类机制的波达方向估计以分辨率高、噪声鲁棒性强等方面的优势也日益受到人们的重视. 稀疏信号重构过程本质上可表征为l0范数下的优化问题,然而由于l0范数问题已被证明是NP难问题[4],因此文献[5-7]利用l1范数替代l0范数进行稀疏重构,并开拓了l1-SVD、NSW-l1等经典稀疏DOA估计方法. 为了进一步逼近l0范数,Goroditsky等[8]提出了一种迭代加权最小范数算法(FOCUSS),该算法将l1范数约束扩展为lp(0 针对上述问题,本文提出了一种新的基于稀疏空间谱匹配的高分辨率DOA估计方法,该方法通过对过完备基矩阵进行奇异值分解,利用TSVD(truncated SVD)方法剔除较小奇异值的影响,利用较大特征值对应的特征向量构建一个良态的矩阵,并用此矩阵替代过完备基,利用lp范数约束正则化FOCUSS算法进行稀疏重构,通过对信源功率的估计实现波达角的估计,解决了网格细划分下过完备基条件数过大带来的病态问题,并采用粗、细两步网格划分策略降低算法复杂度. 计算机仿真结果验证了所提算法的有效性. 假设有K个远场不相关窄带信号从不同的入射方向θk(k=1,2,…,K)入射到M(M>K)元均匀线阵上,阵元间距为d(d≤λ/2,λ为信源波长). 以第一个阵元为相位参考点,高斯白噪声背景下阵列输出可表示为 (1) 式中:s(t)=[s1(t) s2(t) … sK(t)]H为0均值信号向量;n(t)为0均值,方差为σ2的噪声向量;t=1,2,…,T,T为快拍数;A(θ)为M×K的阵列流型矩阵,它的第k列代表第k个信号的导向矢量为 (2) 式中:f为载波频率;c为传播速度. (3) (4) 基于式(4),构造阵列输出信号的协方差矩阵 (5) 式中:E{·}表示数学期望;(·)H表示共轭转置;Rs=E{ s′(t)s′H(t)}=diag[P1P2… PN]为K稀疏的信号协方差矩阵;IM为M×M的单位矩阵. 直接利用文献[5-7,9]中的稀疏重构算法求解式(3)或式(5)的欠定方程组即可得到DOA估计,然而在信源数或快拍数较多的情况下,上述算法的实时性难以保证. 为此,本文对式(5)表示的阵列协方差矩阵进行向量化处理,表示为 (6) (7) (8) (9) (10) (11) 式中λ(>0)为权衡稀疏性和噪声影响的正则化参数,可通过修正l-curve准则确定[11]. 参数p的选择要考虑收敛速度和稀疏性,参数p在0.8~1.0之间选择被证明是收敛速度和稀疏解精确度之间的一个折中选择. 利用式(8)~(11),通过多次迭代可实现对N×1的K稀疏功率矩阵P的估计,由于P与N个可能的入射角度一一对应,从而实现了信源波达角的估计. (12) 本文算法步骤为: ② 采用粗网格(1°~2°)划分并利用式(8)更新迭代结果; 大量仿真实验显示,ε=0.01是一个很好的选择. 同时当预设迭代次数达到15即可满足重构后的稀疏性要求. 本文所提算法涉及的计算复杂度主要包括三部分,阵列协方差矩阵Rx的构建需要的乘法次数为O(M2T),对过完备基进行SVD分解需要O(MN2),基于FOCUSS的稀疏信号重构过程需要O(k(M3+M2N)),其中k代表迭代次数,本文中k=15即可满足稀疏性要求. 而基于MFOCUSS的稀疏信号重构算法的主要计算复杂度分别为O(k(M3+M2N+MNT)). 通常假定M≪N,M 在下面的仿真实验中,考虑一个由7个阵元组成的均匀线阵阵列ULA,阵元间距为0.5倍波长,在窄带复正弦信号和加性高斯白噪声背景下. 仿真实验1:考虑两个窄带非相关信源DOA估计情况,入射角度分别为θ1=5°,θ2=20°,SNR为10 dB,快拍数为200. 图1为以1°在[-90°,90°]范围内进行空间粗网格划分后的空间谱估计结果,图2为以0.2°在[0°,30°]范围内进行空间局部细网格划分后的空间谱估计结果. 从图1和图2可以看出,在网格粗划分下,MUSIC,MFOCUSS和本文方法均具有较好的估计结果,而在局部网格细划分下,由于过完备基条件数过大,MFOCUSS算法出现了较大的估计偏差,而MUSIC方法和本文方法则具有较好的稳健性. 仿真实验2:考虑两个邻近窄带非相关信源DOA估计情况,入射角度分别为θ1=10°,θ2=15°,快拍数为200,以1°在[-90°,90°]范围内进行空间网格划分. 图3和图4分别为SNR为10 dB和SNR为0 dB条件下不同算法的空间谱输出结果. 从图3和图4可以看出在SNR为10 dB条件下除CAPON方法外,均能有效地分辨两个信源,而在SNR为0 dB条件下只有本文方法能有效地分辨两个信源,即本文所提算法具有更高的分辨率. 仿真实验3:为了验证本文所提算法能处理的最大信源个数,在7个阵元下考虑6个窄带非相关信源DOA估计情况,入射角度分别为θ1=-50°,θ2=-30°,θ3=-10°,θ4=10°,θ5=30°,θ6=50°,SNR为10 dB,快拍数为200. 从图5可以看出,本文所提算法和经典的CAPON方法和MUSIC方法一样,在M个阵元下可以有效地估计M-1个信源. 仿真实验4:分别考虑不同SNR和快拍数对MFOCUSS和本文算法估计性能的影响. 实验中,入射角度分别为θ1=-10°,θ2=20°,为保证MFOCUSS算法的有效性,以0.1°在[-90°,90°]范围内进行空间网格划分,而本文算法在1°粗网格划分后以0.1°在[-15°,25°]范围内进行局部细网格划分. 图6为快拍数T=500,信噪比由-10~15 dB时的DOA估计均方根误差随SNR变化结果. 图7为SNR为0 dB,快拍数由100~600时的DOA估计均方根误差随快拍数变化结果. 从图6和图7可以看出,本文算法在信噪比小于5 dB或快拍数大于300条件下具有明显优于MFOCUSS算法的估计性能,同时值得注意的是本文算法可以进行局部精细搜索,因此将具有更高的估计精度和较低的复杂度. 针对网格细划分下过完备基条件数过大对迭代加权最小范数类算法的严重影响,在此基础上提出了一种新的基于空间谱匹配与正则化FOCUSS相结合的稀疏DOA估计方法. 该方法通过对阵列协方差矩阵向量化和采用粗、细两步网格划分策略降低算法复杂度,通过奇异值分解及剔除小奇异值项,解决了网格细划分下过完备基条件数过大时极易受到噪声干扰的问题,算法性能将急剧下降甚至失效,易受噪声干扰的问题带来的病态问题. 最后利用正则化FOCUSS算法进行稀疏重构获得信源DOA参数. 本文方法与经典子空间方法相比,具有更高的分辨率,而与MFOCUSS典型稀疏信号重建算法相比,除具有更高的分辨率外,还具有更好的估计精度和噪声鲁棒性,是一种稳健的高分辨DOA估计算法. [1] Krim H, Viberg M. Two decades of array signal processing research: the parametric approach[J]. IEEE Signal Processing Magazine, 1996,13(4):67-94. [2] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006,52(4):1289-1306. [3] Rao B D. Signal processing with the sparseness constraint[C]∥Proceedings of International Conference on Acoustics, Speech and Signal Processing.[S.l.]: IEEE, 1998:1861-1864. [4] Donoho D L, Viberg M, Kailath T. Stable recovery of sparse overcomplete representation in the presence of noise [J]. IEEE Transactions on Information Theory, 2006,52(1):6-18. [5] Malioutov D, Cetin M, Willsky A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transactions on Signal Processing, 2005,53(8):3010-3022. [6] He Z Q, Liu Q H, Jin L N, et al. Low complexity method for DOA estimation using array covariance matrix sparse representation[J]. Electronics Letters, 2013,49(3):228-230. [7] Yin J H, Chen T Q. Direction-of-arrival estimation using a sparse representation of array covariance vectors[J]. IEEE Transactions on Signal Processing, 2011,59(9):4489-4493. [8] Goroditsky I F, Rao B D. Sparse signal reconstruction from limited data using FOCUSS: a re-weighted minimum norm algorithm[J]. IEEE Transactions on Signal Processing, 1997,45(3):600-616. [9] Cotter S F, Rao B D, Engan K, et al. Sparse solutions to linear inverse problems with multiple measurement vectors [J]. IEEE Transactions on Signal Processing, 2005,53(7):2477-2488. [10] Wang Y, Leus G, Pandharipande A. Direction estimation using compressive sampling array processing[C]∥Proceedings of the 15th IEEE Workshop on Statistical Signal Processing. [S.l.]: IEEE, 2009:626-629. [11] Rao B D, Engan K, Cotter S F, et al. Subset selection in noise based on diversity measure minimization[J]. IEEE Transactions on Signal Processing, 2003,51(3):760-769. [12] Gorodnitsky I F, Beransky D. Fast algorithms for regularized minimum norm solutions to inverse problems[C]∥Proceedings of Conference Record of the Thirtieth Asilomar Conference on Signals, Systems and Computers.[S.l.]:IEEE, 1996:1213-1217. (责任编辑:李兵) High Resolution Direction-of-Arrival Estimation Based on Sparse Spectral Fitting CHEN Jian1, TIAN Ye2, SUN Xiao-ying1 (1.College of Communication and Engineering, Jilin University, Changchun, Jilin 130012, China;2. School of Information Science and Engineering, Yanshan University, Qinhuangdao, Hebei 066004,China) In this paper, a novel high-resolution direction-of-arrival estimation method was presented based on sparse spectral fitting to overcome the drawback that the performance of iterative re-weighted least squares algorithm could be impacted with the overcomplete basis matrix condition number. A singular value decomposition (SVD) was employed to handle the overcomplete basis, adopting the truncated SVD (TSVD) method to remove those singular vectors that corresponded with smaller singular value and obtain a well-conditioned matrix, and using this matrix to replace the overcomplete basis matrix. Then a regularized FOCUSS algorithm withlpnorm constraint was applied for sparse signal reconstruction to resolve ill-posed problem when the overcomplete basis matrix condition number got too large, and coarse-refined space grid separation was used to decrease the computational complexity. Simulation results show that compared with MFOCUSS algorithm, the proposed method can not only reduce computational complexity, but also hold much higher resolution and robustness to noise. direction of arrival; sparse signal reconstruction; overcomplete basis; FOCUSS; singular value decomposition(SVD) 2014-04-25 国家自然科学基金资助项目(61171137) 陈建(1977—),男,讲师,E-mail:chenjian@jlu.edu.cn; 田野(1985—),男,博士生,E-mail:tianfield@126.com;孙晓颖(1969—),男,教授,博士生导师,E-mail:sunxy@jlu.edu.cn. TN 911.7 A 1001-0645(2016)10-1043-05 10.15918/j.tbit1001-0645.2016.10.0111 稀疏信号模型
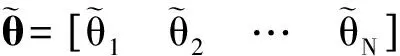
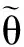
2 稀疏DOA估计算法
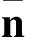
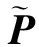
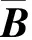
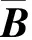
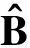
3 仿真实验
4 结 论

