数系的扩充与复数的引入中的误区警示
■陕西省洋县中学 刘大鸣(特级教师)
数系的扩充与复数的引入中的误区警示
■陕西省洋县中学 刘大鸣(特级教师)
警示一:混淆实数和复数的概念和性质适用的范围
例1 (2015年广东汕头市模拟试题)下列命题中,正确的命题的个数是( )。
(1)若z∈C, 则z2≥0;(2)若z1,z2∈C,且z1-z2>0,则z1>z2;(3)若a>b,则a+i>b+i;(4)若x,y∈C,则x+yi=1+i的充要条件是x=y=1;(5)若x2+y2=0,则x=y=0。
A. 0 B. 1 C. 2 D.5
错解:D。
误区:命题(1)误把任何一个实数的平方大于零推广到复数中。命题(2)误认为两实数之差大于零等价于前一个实数大于后一个实数,也推广到复数中来,认为两复数差为实数则这两个复数也为实数。命题(3)把不等式性质错误地推广到复数中,忽略不等式是在实数中才成立的。命题(4) 误认为x,y一定是x+yi的实部和虚部。命题(5)误认为x,y是实数。
正解:(1)假命题,反例设z=i,则z2=i2=-1<0。
(2)假命题,反例设z1=2+i,z2=1+i,满足z1-z2=1>0,但z1,z2不能比较大小。
(3)假命题,a>b,a,b∈R,故a+i,b+i都是虚数,不能比较大小。
(4)假命题,由于x,y∈C,所以x,y不一定是x+yi的实部和虚部,故是假命题
(5)假命题,没有说明x,y是实数,不妨构造反例12+i2=0,但1≠0,i≠0。
综上可知,答案为A。
点评:复数与实数的不同之处在于:任意两个实数可以比较大小,而任意两个复数中只要有一个不是实数时就不能比较大小。以前学过的函数、不等式等都是在实数范围内研究的。
警示二:将实数的运算法则或性质迁移到复数中
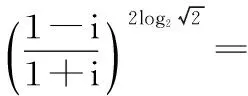

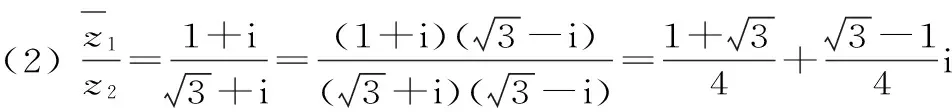
误区:错解中(1)是对复数的运算法则理解错误造成的,(2)是同学们经常会误认为“虚部”应该含有虚数单位i而导致的。

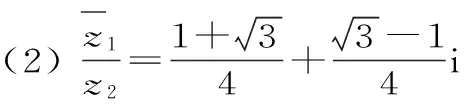
点评:复数的加法满足交换律、结合律,即对任何z1,z2,z3∈C,有z1+z2=z2+z1,(z1+z2)+z3=z1+(z2+z3)。复数的乘法不仅满足交换律与结合律,实数集R中整数指数幂的运算律,在复数集C中仍然成立。

(2)形如z=a+bi(a,b∈R)的数叫做复数,a叫做复数的实部,b叫做复数的虚部。
警示三:忽视in的周期性引发错误
例3 已知n∈N*,求值:
(1+i)n·(1-i)6-n=____。

误区:需求出该式子的所有可能取值,in的值具有以4为周期的特点,根据n求in必须按被4整除,余数为0,1,2,3四种情况进行分类讨论。

=(-2i)3·in=8in+1
点评:复数运算中的结论:
(1)(1±i)2=±2i。


(4)i的周期性为:①i4k=1,i4k+1=i,i4k+2=-1,i4k+3=-i,k∈N*;②ik+ik+1+ik+2+ik+3=0,k∈N*。
警示四:用实数系方程的解法来探究复数系方程的根
例4 若关于x的方程x2-(2i-1)x+3m-i=0有实根,求m的取值。

误区:实数系一元二次方程有实根的判定方法是判别式Δ≥0,但对于复数系一元二次方程并不适用。
正解:依据根的意义设根,利用复数相等的充要条件,转化求解。
设方程x2-(2i-1)x+3m-i=0的实根为a,则由根的定义可得:a2-(2i-1)a+3m-i=0。所以(a2+a+3m)-(2a+1)i=0。由复数相等定义可知:
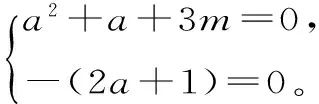
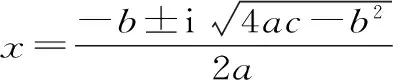
警示五:研究复轨迹方程时忽略其几何意义
A.椭圆 B.直线 C.线段 D.圆
错解:选A或B。



可得到复平面内复数z对应的点的几个基本轨迹:
(1)|z-z0|=r(r是正常数),轨迹是一个圆。
(2)|z-z1|=|z-z2|(z1、z2是复常数),轨迹是一条直线。
(3)|z-z1|+|z-z2|=2a(z1、z2是复常数,a是正常数),轨迹有三种可能情形:①当2a>|z1-z2|时,轨迹为椭圆;②当2a=|z1-z2|时,轨迹为一条线段;③当2a<|z1-z2|时,轨迹不存在。
(4)||z-z1|-|z-z2||=2a(a是正常数),轨迹有三种可能情形:①当2a<|z1-z2|时,轨迹为双曲线;②当2a=|z1-z2|时,轨迹为两条射线;③当2a>|z1-z2|时,轨迹不存在。
警示六:用轨迹求最值时忽略隐含条件
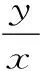

图1
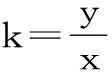
误区:忽略虚数(x-2)+yi的条件致使所求斜率的范围扩大。

图2

注意斜率的意义和点不在x轴上的特点,选B。
点评:复数与向量有着天然的联系,借助复数模的几何意义可以得到某些轨迹方程,利用轨迹求最值时既要考虑目标函数的几何意义(斜率,截距,距离等),又要注意其隐含条件对所求最值的影响。
警示七:利用复数差的几何意义探究网络交汇问题
A.(0,1) B.(0,1]
C.[0,1) D.[0,1]
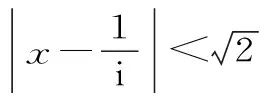
y=|cos2x-sin2x|=|cos 2x|∈[0,1],即M=[0,1]。
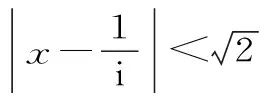
M∩N=[0,1),故选C。
点评:所求集合分别为对应函数的值域和不等式的解集,可利用有界性求三角函数的值域。复数差的模构成的一元二次不等式,可解不等式得到解集,再求交集。本题将不等式的解集用复数差的模进行合理包装,是高考复数命题的一个创新,耐人回味。
练一练:
(2015年陕西高考)设复数z=(x-1)+yi(x,y∈R),若|z|≤1,则y≥x的概率为( )。
答案:B。
(责任编辑 徐利杰)

