数系的扩充与复数的引入单元测试题
■河北省枣强中学 郭统福
数系的扩充与复数的引入单元测试题
■河北省枣强中学 郭统福
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符号题目要求的)

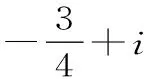
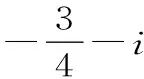
A.1 B.3 C.-4 D.-5
3.若复数z满足(2-i)z=|1+2i|,则z的虚部为( )。
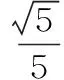
4.复数z满足(1+2i)z=4+ai(a∈R,i是虚数单位),若复数z的实部与虚部相等则a等于( )。
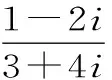
A.第四象限 B.第三象限
C.第二象限 D.第一象限

A.圆 B.椭圆
C.双曲线 D.抛物线
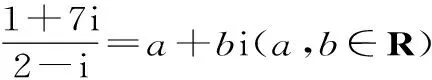
A.-15 B.3 C.-3 D.15
8.i+i2+i3+…+i2 014=( )。
A.1+i B.-1-i
C.1-i D.-1+i
9.“复数z为实数”的充分而不必要条件是( )。


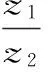

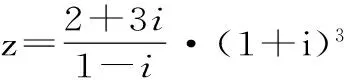
A.复平面内复数z对应的点在第一象限
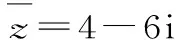
C.若复数z1=z+b(b∈R)为纯虚数,则b=4

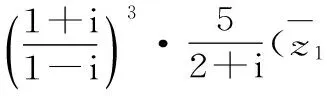
A.第一象限 B.第二象限
C.第三象限 D.第四象限
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
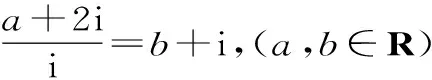

16.给出下列的命题:
(1)若z∈C,则z2≥0;
(2)若a,b∈R,且a>b,则a+i>b+i;
(3)若a∈R,则(a+1)i是纯虚数;
(4)若z=-i,则z3+1在复平面内对应的点位于第一象限。其中正确的命题是____。(填上所有正确的命题的序号)
三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明,证明过程或演算步骤)
17.(本题10分)当实数m取何值时,复数z=(m2-3m+m2i)-[4+(5m+6)i]为实数?为虚数?为纯虚数?
18.(本题12分)已知复数z=1+i。
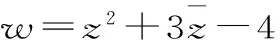

19.(本题12分)设复数z=(a2-4sin2θ)+(1+2cosθ)i,其中i为虚数单位,a为实数,θ∈(0,π)。若z是方程x2-2x+5=0的一个根,且z在复平面内所对应的点在第一象限,求θ和a的值
20.(本题12分)已知x,y为共轭复数,且(x+y)2-3xyi=4-6i,求x,y。
(1)求z2;
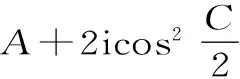

(1)求|z|的值及z的实部的取值范围;
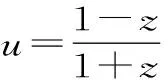
(3)求ω-u2的最小值。

7.C 8.D 9.B 10.C 11.C 12.B
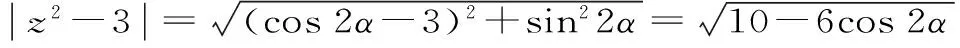
15.-1 16.(4)
17.先把复数z整理成z=(m2-3m-4)+(m2-5m-6)i。
(1)当m2-5m-6=0,即m=-1或m=6时,z是实数。
(2)当m2-5m-6≠0,即m≠-1且m≠6时,z是虚数。
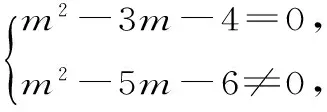
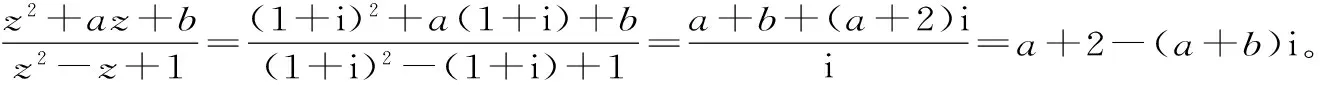

19.方程x2-2x+5=0的根为x=1±2i,因为z在复平面内所对应的点在第一象限,所以z=1+2i。
即(a2-4sin2θ)+(1+2cosθ)i=1+2i。
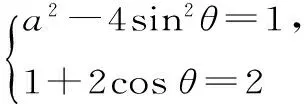
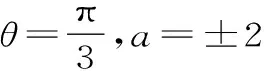
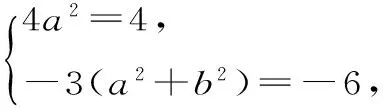
故所求的复数为:
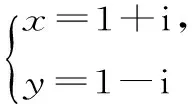
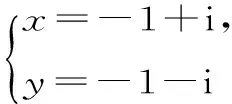
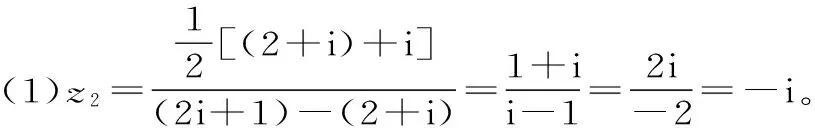
(2)在△ABC中,由于内角A、B、C依次成等差数列, 则B=60°,A+C=120°。
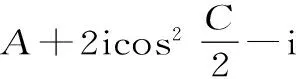
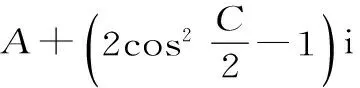
=cosA+icosC。
所以|μ+z2|2=cos2A+cos2C
=cos (A+C)cos (A-C)+1
=1+cos 120°cos(A-C)
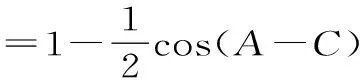
由于A+C=120°,所以A-C=120°-2C。因此-120° 22.(1)因为z是虚数,所以可设z=x+yi,x,y∈R,且y≠0。 则x2+y2=1,即|z|=1。此时ω=2x。 因此,u为纯虚数。 ω-u2的最小值为1,此时z=±i。 (责任编辑 徐利杰)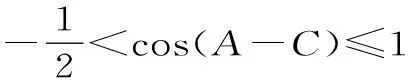
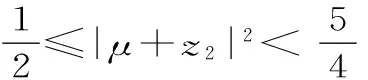
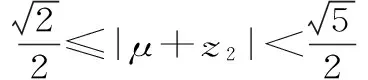
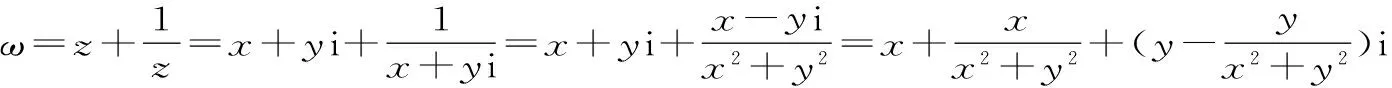
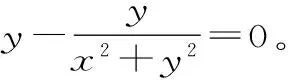
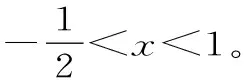
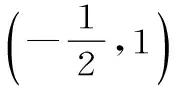
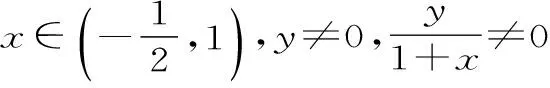
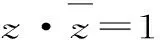
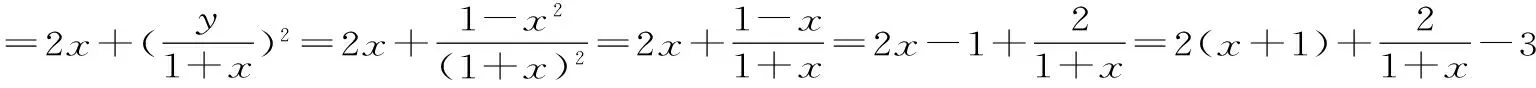
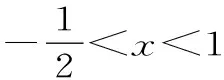
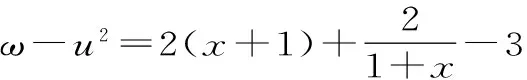
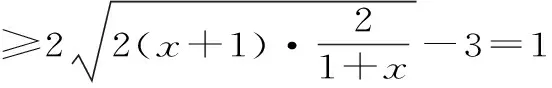
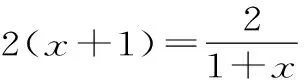
- 中学生数理化(高中版.高二数学)的其它文章
- 烃和氯代烃相关知识检测
- 有关烃类燃烧重要规律剖析
- 烃的知识大突破
- 关注电表内阻 翻转电学实验
- 恒定电流基本知识汇总
- 《推理与证明》必刷题汇集

