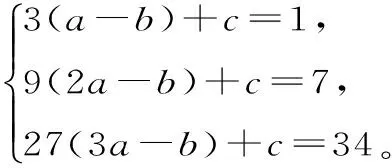《推理与证明》必刷题汇集

■江苏省张家港职业教育中心校 韩文美



《推理与证明》必刷题汇集

■江苏省张家港职业教育中心校 韩文美

一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符号题目要求的)

A．第6项 B．第7项

C．第19项 D．第11项

2．有一段演绎推理是这样的：有些有理数是真分数，整数是有理数，则整数是真分数。结论显然是错误的，这是因为( )。

A．大前提错误 B．小前提错误

C．推理形式错误 D．以上说法都不是

A．1 B．1+2

C．1+2+3 D．1+2+3+4

4．观察数列1，2，2，3，3，3，4，4，4，4，…，的特点，按此规律，则第100项为( )。

A．10 B．14 C．13 D．100

5．下列说法正确的是( )。

A．“a

B．命题“∀x∈R，x3-x2-1≤0”的否定是“∃x∈R，x3-x2-1≤0”

C．“若a、b都是奇数，则a+b是偶数”的逆否命题是“若a+b不是偶数，则a、b不都是奇数”

D．如果p∧q为假命题，那么p、q均为假命题

6．下列代数式(其中k∈N*)能被9整除的是( )。

A．6+6·7kB．2+7k-1

C．2(2+7k+1) D．3(2+7k)

8．已知a+b+c=0，则ab+bc+ca的值( )。

A．大于0 B．小于0

C．不小于0 D．不大于0

A．a>bB．a

C．a=bD．a、b的大小不定

10．已知1+2×3+3×32+4×33+…+n×3n-1=3n(na-b)+c对一切n∈N*都成立，那么a、b、c的值为( )。

D．不存在这样的a、b、c

11．设函数f(x)定义如下表，数列{xn}满足x0=5，且对任意的自然数均有xn+1=f(xn)，则x2 016=( )。

x12345f(x)41352

A．1 B．2 C．4 D．5

12．已知数列{xn}满足xn+3=xn，xn+2=|xn+1-xn|(n∈N*)，若x1=1，x2=a(a≤1，a≠0)，则数列{xn}的前2 016项的和S2 016的值为( )。

A．672 B．1 344

C．2 016 D．2 688

二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)

14．有甲、乙、丙、丁四位歌手参加比赛，其中只有一位获奖，有人走访了四位歌手，甲说：“是乙或丙获奖。”乙说：“甲、丙都未获奖。”丙说：“我获奖了。”丁说：“是乙获奖。”四位歌手中只有两人的话是正确的，则获奖的歌手是____。

16．在平面上，我们用一直线去截正方形的一个角，那么截下的一个直角三角形，按如图1所示，由勾股定理知c2=a2+b2。设想把正方形换成正方体，把截线换成截面，如图2，这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN，如图3所示，如果用S1、S2、S3表示三个侧面面积，S表示截面面积，那么类比得到的结论是____。

图1 图2 图3

三、解答题(本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)

19．(本题12分)我们知道，在△ABC中，若c2=a2+b2，则△ABC是直角三角形。现在请你研究：若cn=an+bn(n>2)，则△ABC为何种三角形？为什么？

(1)证明：函数f(x)在(-1，+∞)上为增函数；

(2)用反证法证明方程f(x)=0没有负数根。

(1)求函数f(x)的单调区间和极值；

22．(本题12分)设f(n)是定义在N*上的增函数，f(4)=5，且满足：

①任意n∈N*，f(n)∈Z；

②任意m，n∈N*，有f(m)·f(n)=f(mn)+f(m+n-1)。

(1)求f(1)，f(2)，f(3)的值；

(2)求f(n)的表达式。

参考答案

1．B 2．C 3．D 4．B 5．C 6．D 7．D 8．B 9.B

11．D 提示：由于x1=f(x0)=f(5)=2，x2=f(2)=1，x3=f(1)=4，x4=f(4)=5，x5=f(5)=2，…，归纳可得数列{xn}是周期为4的数列，所以x2 016=x0=5。

12．B 提示：根据题意，x3=|x2-x1|=|a-1|=1-a(a≤1，a≠0)，则x1+x2+x3=2。又xn+3=xn，所以x4=x1，x5=x2，x6=x3，即x4+x5+x6=x1+x2+x3=2。同理，x7+x8+x9=2，…，x3n+1+x3n+2+x3n+3=2，而2 016=672×3，则S2 016=2×672=1 344。

14．丙 提示：若甲获奖，则甲、乙、丙、丁说的都是错的，同理可推知乙、丙、丁获奖的情况，最后可知获奖的歌手是丙。

17．由a2+b2≥2ab，及b2+c2≥2bc，c2+a2≥2ca，以上三式相加整理得：

a2+b2+c2≥ab+bc+ca。

则3(a2+b2+c2)≥(a2+b2+c2)+2(ab+bc+ca)=(a+b+c)2。

由a+b+c=1，得3(a2+b2+c2)≥1。

证明如下：设A(x0，y0)为椭圆上的任意一点，则A关于椭圆中心的对称点B的坐标为B(-x0，-y0)，点P(x，y)为椭圆上异于A，B两点的任意一点，则：

19．△ABC为锐角三角形。

证明过程如下：cn=an+bn(n>2)，c>a，c>b，由于c是△ABC的最大边，所以要证△ABC是锐角三角形，只需证角C为锐角，即证cosC>0。

证cosC>0，只要证a2+b2>c2。

①

注意到条件：an+bn=cn，于是将①等价变形为：(a2+b2)cn-2>cn。

②

因为c>a，c>b，n>2，所以cn-2>an-2，cn-2>bn-2，即cn-2-an-2>0，cn-2-bn-2>0。

从而(a2+b2)cn-2-cn=(a2+b2)cn-2-an-bn=a2(cn-2-an-2)+b2(cn-2-bn-2)>0，这说明②式成立，从而①式也成立。

故cosC>0，C是锐角，△ABC为锐角三角形。

20．(1)任取x1，x2∈(-1，+∞)，不妨设x10，ax2-x1>1且ax1>0。

ax2-ax1=ax1(ax2-x1-1)>0。

x1+1>0，x2+1>0。

故函数f(x)在(-1，+∞)上为增函数。

故方程f(x)=0没有负数根。

21．(1)f′(x)=(x-1)(ex-1)。

当x<0或x>1时，f′(x)>0；

当0

f(x)在(-∞，0)和(1，+∞)上单调递增，在(0，1)上单调递减。

当x=0时，f(x)有极大值f(0)=0；

22．(1)因为f(1)f(4)=f(4)+f(4)，所以5f(1)=10，则f(1)=2。

因为f(n)是单调增函数，所以2=f(1)

因为f(n)∈Z，所以f(2)=3，f(3)=4。

(2)由f(1)=2，f(2)=3，f(3)=4，f(4)=5，猜想f(n)=n+1。

下面用数学归纳法证明：

①当n=1，2，3，4时，命题成立；

②假设当n=k(k≥4)时，命题成立，下面讨论n=k+1的情形。

即f(k+2)=k+3。

又k+1=f(k)

因此不论k的奇偶性如何，总有f(k+1)=k+2，即n=k+1时，命题也成立。

于是对一切n∈N*，f(n)=n+1。

(责任编辑 徐利杰)