VISCOSITY APPROXIMATION METHODS FOR THE SPLIT EQUALITY COMMON FIXED POINT PROBLEM OF QUASI-NONEXPANSIVE OPERATORS∗

Jing ZHAOCollege of Science,Civil Aviation University of China,Tianjin 300300,China Tianjin Key Laboratory for Advanced Signal Processing,Tianjin 300300,China E-mail:zhaojing200103@163.com

Shengnan WANGCollege of Science,Civil Aviation University of China,Tianjin 300300,China E-mail:shengnan19900507@163.com

VISCOSITY APPROXIMATION METHODS FOR THE SPLIT EQUALITY COMMON FIXED POINT PROBLEM OF QUASI-NONEXPANSIVE OPERATORS∗

Let H1,H2,H3be real Hilbert spaces,let A:H1→H3,B:H2→H3be two bounded linear operators.The split equality common fixed point problem(SECFP)in the infinite-dimensional Hilbert spaces introduced by Moudafi(Alternating CQ-algorithm for convex feasibility and split fixed-point problems.Journal of Nonlinear and Convex Analysis) is

where U:H1→H1and T:H2→H2are two nonlinear operators with nonempty fixed point sets F(U)={x∈H1:Ux=x}and F(T)={x∈H2:Tx=x}.Note that, by taking B=I and H2=H3in(1),we recover the split fixed point problem originally introduced in Censor and Segal.Recently,Moudafi introduced alternating CQ-algorithms and simultaneous iterative algorithms with weak convergence for the SECFP(1)of firmly quasi-nonexpansive operators.In this paper,we introduce two viscosity iterative algorithms for the SECFP(1)governed by the general class of quasi-nonexpansive operators.We prove the strong convergence of algorithms.Our results improve and extend previously discussed related problems and algorithms.

split equality common fixed point problems;quasi-nonexpansive operator; strong convergence;viscosity iterative algorithms;Hilbert space 2010 MR Subject Classification47H09;47H10;47J05;54H25

1　Introduction

The split equality common fixed point problem(SECFP)was investigated recently,which is a generalization of the split feasibility problem and of the convex feasibility problem.The SECFP attracted many authors’attention due to its extraordinary utility and broad applicability in many areas of applied mathematics(most notably,fully-discretized models inverse problems which arise from phase retrievals and in medical image reconstruction[1]).Various algorithms were invented to solve it(see[2–6]).In this paper,our interest is in the study of the convergence of two viscosity iterative algorithms for the following SECFP introduced by Moudafi[7]:

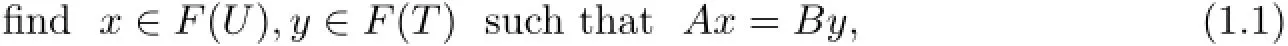
where A:H1→H3and B:H2→H3are two bounded linear operators,U:H1→H1and T:H2→H2are two nonlinear operators with nonempty fixed point sets F(U)=C and F(T)=Q.This allows asymmetric and partial relations between the variables x and y. The interest is to cover many situations,for instance in decomposition methods for PDE’s, applications in game theory and in intensity-modulated radiation therapy(IMRT).In decision sciences,this allows to consider agents who interact only via some components of their decision variables(see[8]).In IMRT,this amounts to envisage a weak coupling between the vector of doses absorbed in all voxels and that of the radiation intensity(see[9]).

To begin with,let us recall that the split feasibility problem(SFP)is to find a point

where C and Q are nonempty closed convex subset of real Hilbert spaces H1and H2,respectively,and A:H1→H2is a bounded linear operator.The SFP in finite-dimensional Hilbert spaces was originally introduced by Censor and Elfving[1o].Many algorithms were invented to solve it(see[3–5,1o–15]and references therein).

Note that if the split feasibility problem(1.2)is consistent(i.e.,(1.2)has a solution),it is no hard to see that x∗solves the SFP(1.2)if and only if it solves the fixed point equation

where PCand PQare the(orthogonal)projection onto C and Q,respectively,γ>o is any positive constant and A∗denotes the adjoint of A.This implies that we can use fixed point algorithms(see[12,16,17])to solve SFP.

To solve(1.3),Byrne[1]proposed his CQ algorithm which generates a sequence{xk}by

Censor and Segal[18]considered the following split common fixed point problem(SCFP):

where A:H1→H2is a bounded linear operator,U:H1→H1and T:H2→H2are two nonexpansive operators with nonempty fixed point sets F(U)=C and F(T)=Q.

To solve(1.4),Censor and Segal[18]proposed and proved,in finite-dimensional spaces,the convergence of the following algorithm:

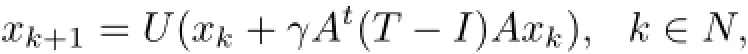
For solving the SECFP(1.1),Moudafi[7]introduced the following alternating algorithm

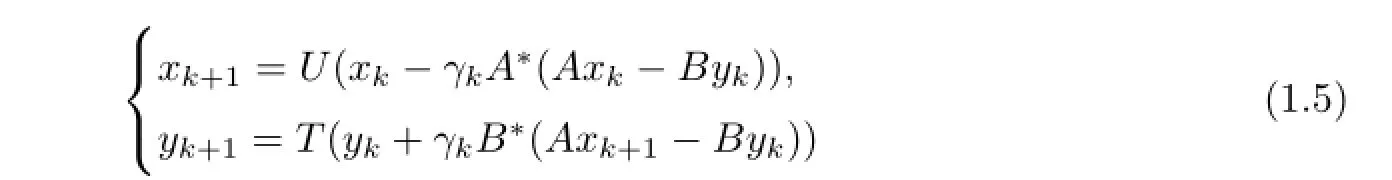
for firmly quasi-nonexpansive operators U and T,where non-decreasing sequence γk∈(ε,stand for the spectral radius of AA and BB,respectively.∗∗

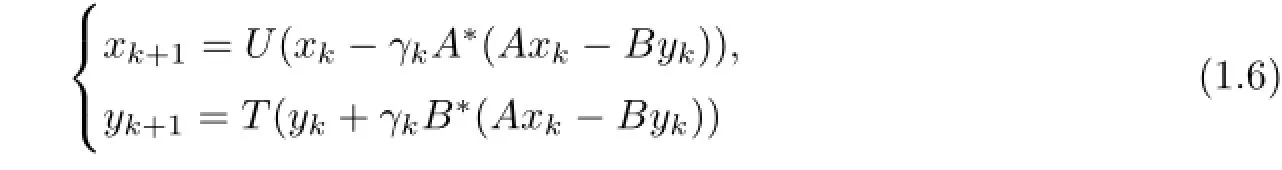
Very recently,Moudafi[19]introduced the following simultaneous iterative method to solve SECFP(1.1): for firmly quasi-nonexpansive operators U and T,whereλA,λBstand for the spectral radius of A∗A and B∗B,respectively.

For solving SCFP(1.4)of quasi-nonexpansive operators,Moudafi[6]introduced the following relaxed algorithm

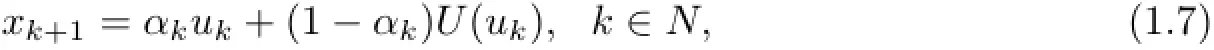
where uk=xk+γβA∗(T−I)Axk,β∈(o,1),αk∈(o,1)and γ∈with λ being the spectral radius of the operator A∗A.Moudafi proved weak convergence result of the algorithm in Hilbert spaces.

Recently,Zhao and He[2o]introduced the following viscosity approximation algorithm for the SCFP(1.4)of quasi-nonexpansive operators

where T=U(I+γA∗(S−I)A),A:H1→H2is a bounded linear operator,U:H1→H1and S:H2→H2are two quasi-nonexpansive operators with nonempty fixed point sets F(U)=C and F(T)=Q,f:H1→H1is a contraction of modulus ρ∈[o,1),such that,with λ being the spectral radius of the operator A∗A and αk∈(o,1).We can obtain the strong convergence of the sequence given by(1.8)to the unique solution of the variational inequality problem VIP(I−f,Γ):

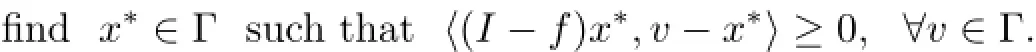
Inspired and motivated by the works mentioned above,we introduce two viscosity iterative algorithms for solving the SECFP(1.1)for the general class of quasi-nonexpansive operators. The organization of this paper is as follows.Some useful definitions and results are listed for the convergence analysis of the iterative algorithms in Section 2.In Section 3,the strong convergence theorems of the proposed viscosity iterative algorithms are obtained.

2　Preliminaries

Thought this paper,we always assume that H is a real Hilbert space with the inner product〈·,·〉and the norm‖·‖.Let I denote the identity operator on H.Let T:H→H be a operator.A point x∈H is said to be a fixed point of T provided Tx=x.In this paper,we use F(T)to denote the fixed point set of T.We use→and⇀to denote the strong convergence and weak convergence,respectively.We use ωw(xk)={x:∃xkj⇀x}stand for the weak ω-limit set of {xk}and use Γ stand for the solution set of the SECFP(1.1).

Definition 2.1An operator T:H→H is said to be

(i)nonexpansive if‖Tx−Ty‖≤‖x−y‖for all x,y∈H;

(ii)quasi-nonexpansive if F(T)/=Ø and if‖Tx−q‖≤‖x−q‖for all x∈H and q∈F(T);

(iii)firmly nonexpansive if‖Tx−Ty‖2≤‖x−y‖2−‖(x−y)−(Tx−Ty)‖2for all x,y∈H;

(iv)firmly quasi-nonexpansive if F(T)/=Ø and if‖Tx−q‖2≤‖x−q‖2−‖x−Tx‖2for all x∈H and q∈F(T).

Definition 2.2An operator T:H→H is called demiclosed at the origin if,for any sequence{xn}which weakly converges to x,and if the sequence{Txn}strongly converges to o,then Tx=o.

Definition 2.3An operator T:H→H is called contraction with constant ρ∈[o,1)if, for any x,y∈H,

In real Hilbert space,we easily get the following equality:

In what follows,we give some properties of the relaxed operator Tα=αI+(1−α)T for quasi-nonexpansive operators which will be needed in our main theorem.

Lemma 2.4(see[6])Let H be a real Hilbert space and T:H→H a quasi-nonexpansive operator.Set Tα=αI+(1−α)T for α∈[o,1).Then,the following properties are reached for all(x,q)∈H×F(T):

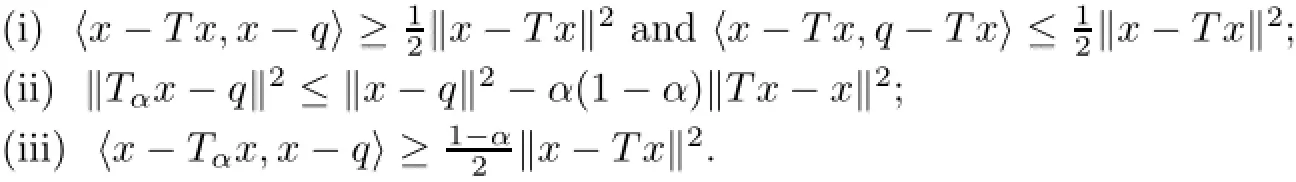
Remark 2.5Let Tα=αI+(1−α)T,where T:H→H is a quasi-nonexpansive operator and α∈[o,1).We have F(Tα)=F(T)and‖Tαx−x‖2=(1−α)2‖Tx−x‖2.It follows from (ii)of Lemma 2.4 thatwhich implies that Tαis firmly quasi-nonexpansive operator when

We end this section by following lemmas,which are important in convergence analysis for our iterative algorithms.

Lemma 2.6(see[21])Assume{sk}is a sequence of nonnegative real numbers such that

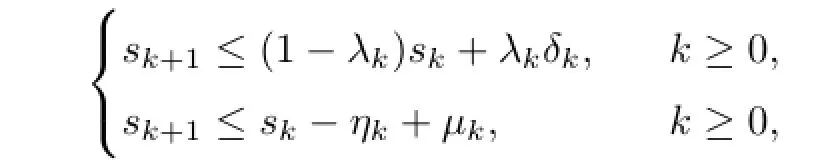
where{λk}is a sequence in(o,1),{ηk}is a sequence of nonnegative real numbers and{δk} and{µk}are two sequences in ℝ such that

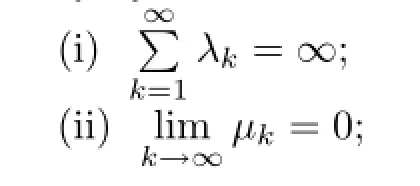
Lemma 2.7(see[22])Let H be a real Hilbert space.Then for all t∈[o,1]and x,y∈H,

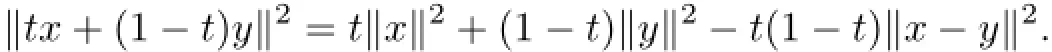
3　Strong Convergence Result of Viscosity Approximation Methods for SECFP(1.1)

In this section,we introduce two viscosity iterative algorithms for SECFP(1.1)of quasinonexpansive operators and prove strong convergence of the algorithms.

Theorem 3.2Let H1,H2,H3be real Hilbert spaces.Given two bounded linear operators A:H1→H3,B:H2→H3,let U:H1→H1and T:H2→H2be quasi-nonexpansive operators with the solution set Γ of(1.1)is nonempty.Assume that the following conditions are satisfied:

(3)U−I and T−I are demiclosed at origin;

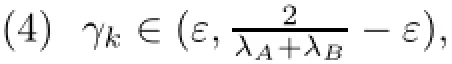
where λA,λBstand for the spectral radius of A∗A and B∗B respectively and ε is small enough;

Then the sequence{(xk,yk)}generated by Algorithm 3.1 strongly converges to a solution (x∗,y∗)of(1.1)which solves the variational inequality problem

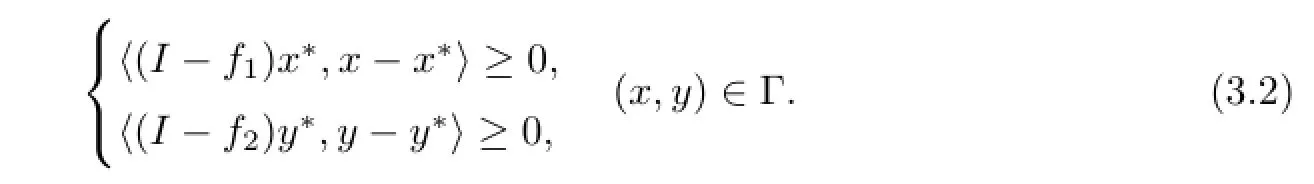
ProofLet(x∗,y∗)∈Γ be the solution of the variational inequality problem(3.2).Then x∗∈F(U),y∗∈F(T)and Ax∗=By∗.We have

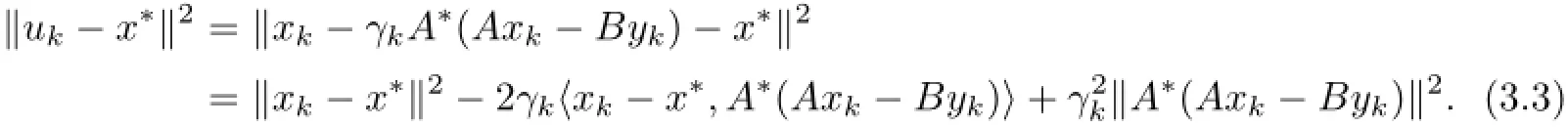
It follows from the definition of λAthat

Using equality(2.1),we have

假设整个无线传感器网络由n个无线传感器节点和1个汇聚节点构成,每个无线传感器节点的采样周期为Δt,每个数据重构周期由m个采样周期构成.在每个数据重构周期内,传感器网络中第i个无线传感器节点的感知数据构成向量xi=[xi,Δt,xi,2Δt,…,xi,mΔt]T,其中xi,jΔt为第i个传感器节点在第j个采样周期所感知的监测数据.因此,整个无线传感器网络在该数据重构周期内的所有感知数据构成一个m×n的感知矩阵X=[x1,x2,…,xn].

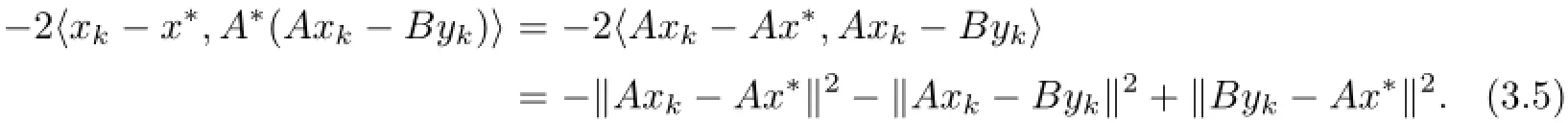
By(3.3)–(3.5),we obtain

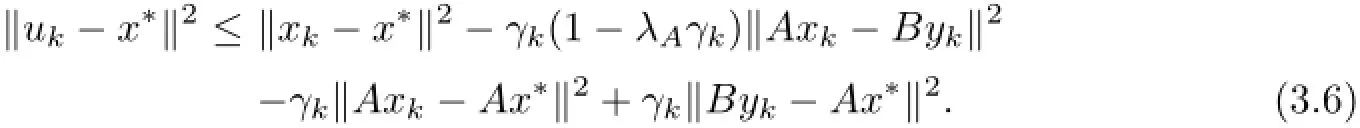
Similarly,we have

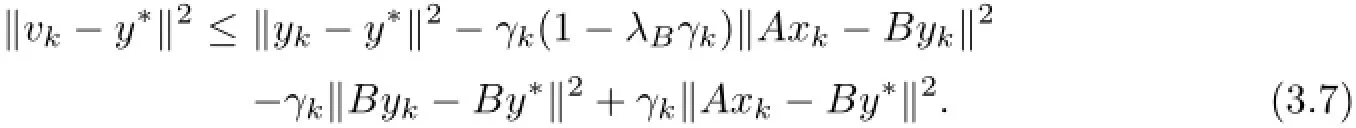
By adding the two last inequalities and by taking into account the fact that Ax∗=By∗,we obtain

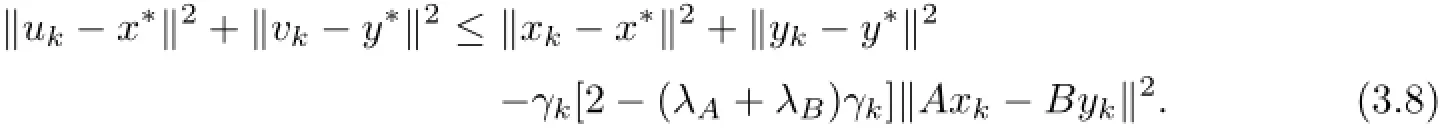
Using the assumption on γkwe obtain

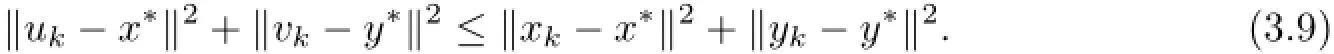
Setting ρ=max{ρ1,ρ2},we have ρ∈By U and T are quasi-nonexpansive operators, it follows from property(ii)of Lemma 2.4 that

Adding up the last two inequalities and using(3.9),settingwe

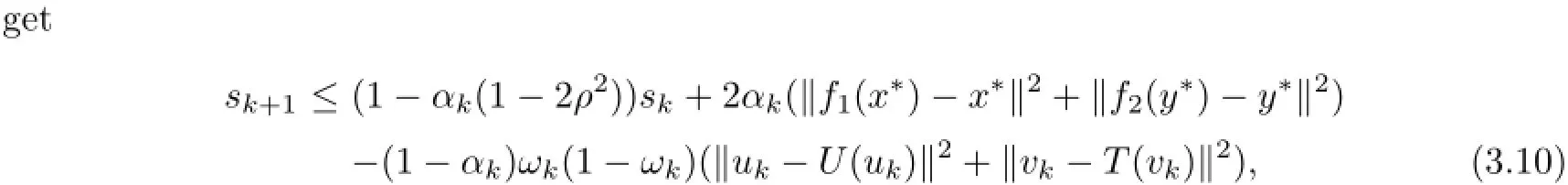
which implies

It follows from induction that

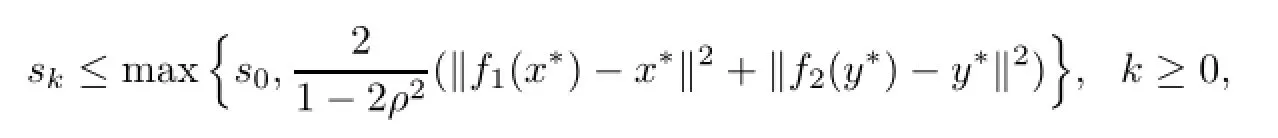
which implies that{xk}and{yk}are bounded.It follows that{uk},{vk},{f1(xk)}and{f2(yk)} are bounded.

Setting˜uk=(1−ωk)uk+ωkU(uk),˜vk=(1−ωk)vk+ωkT(vk),note that U is a quasinonexpansive operator,we have

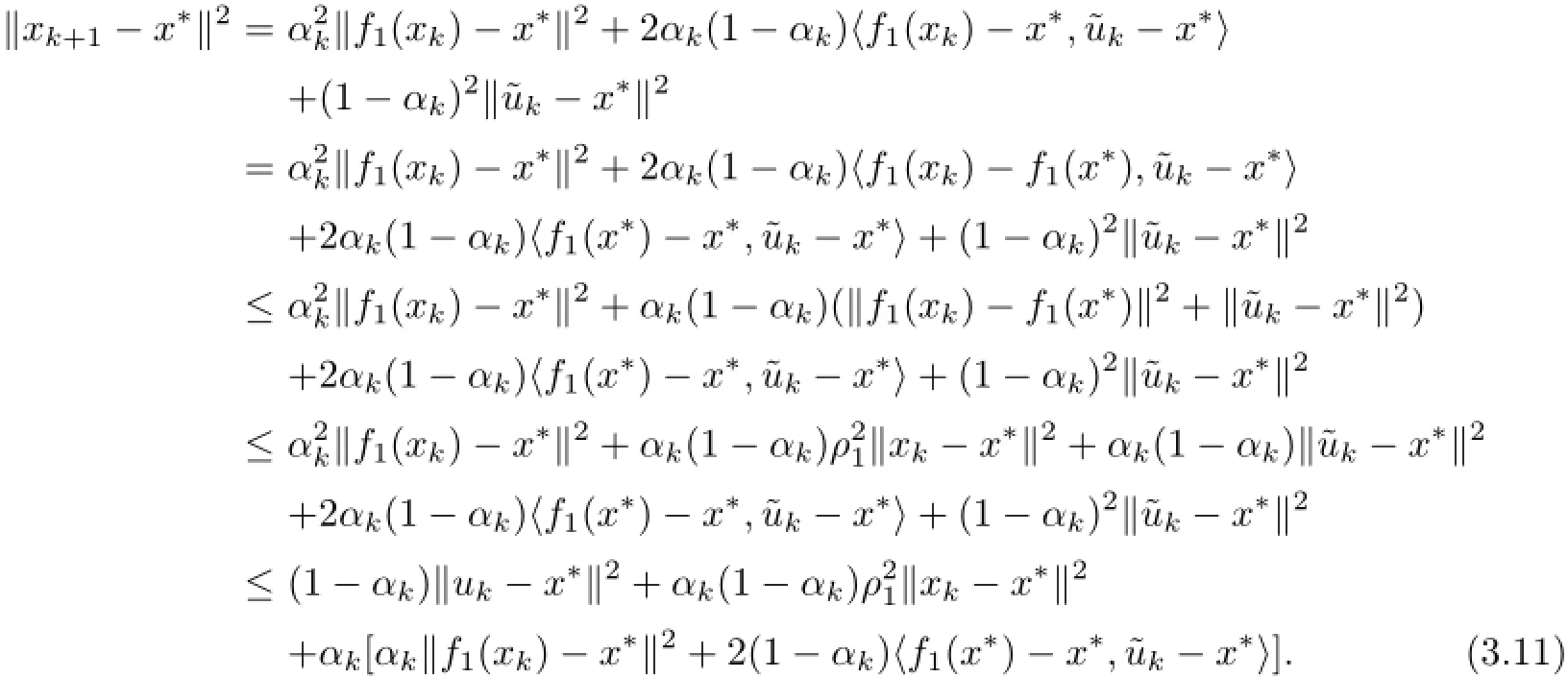
Similarly,we have

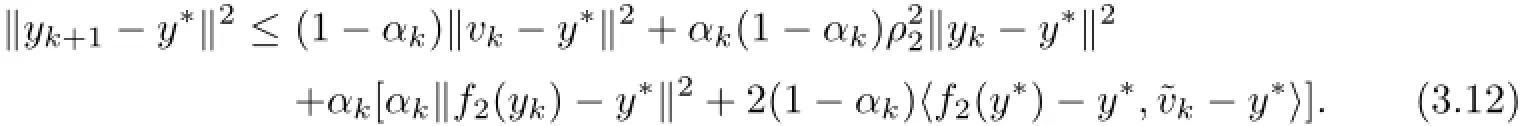
So,by(3.9),(3.11),and(3.12),we obtain

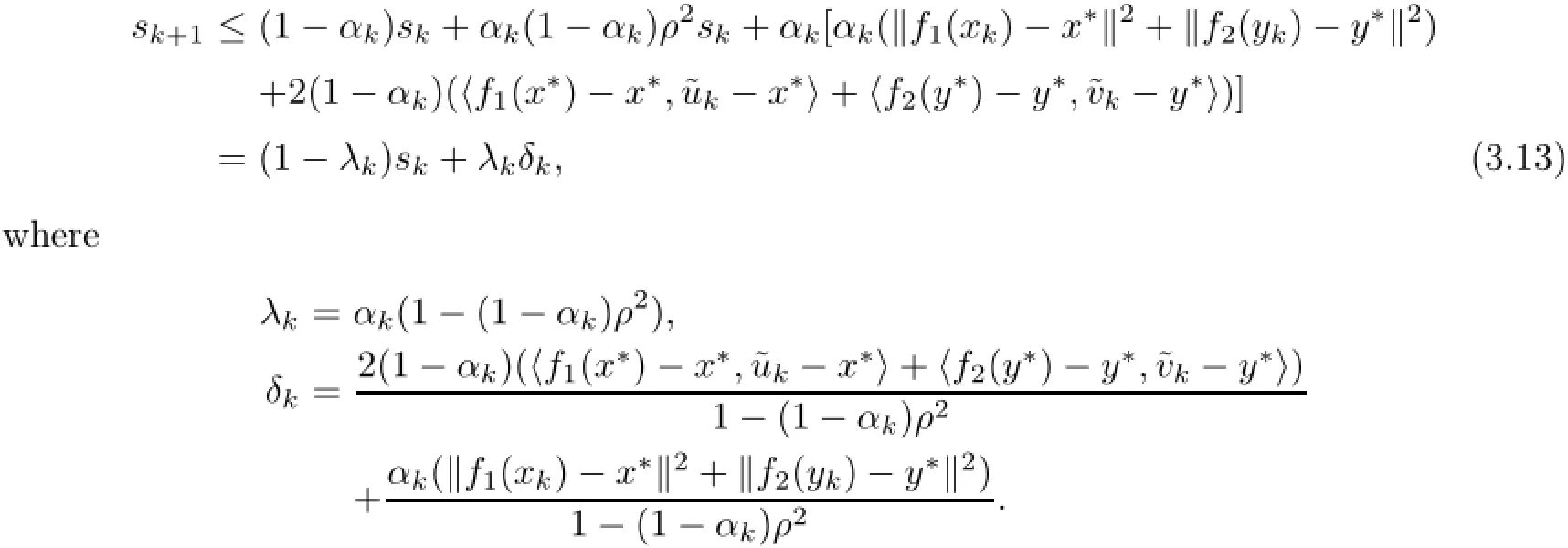
On the other hand,from(3.1)we have

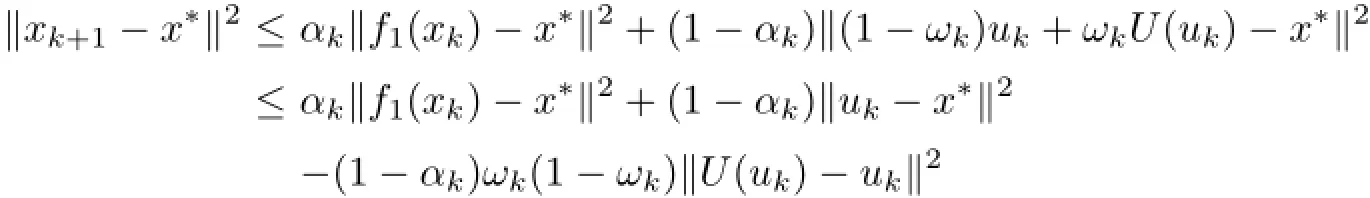
Using(3.8),we obtain

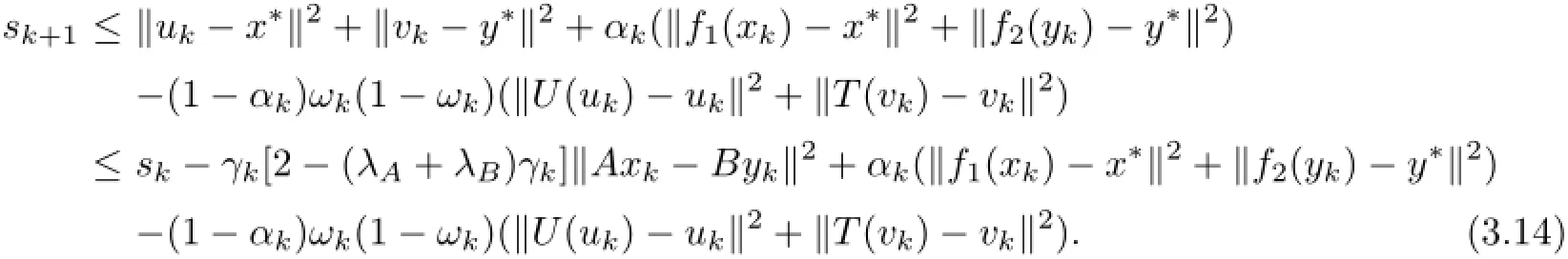
Now,by setting

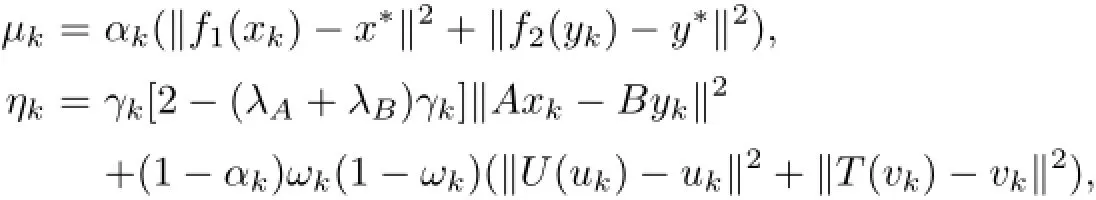
(3.14)can be rewritten as the following form,

By the assumption on α,we get

kwhich thanks to the boundedness of{xk}and{yk}.

To use Lemma 2.6,it suffices to verify that,for all subsequenceimplies

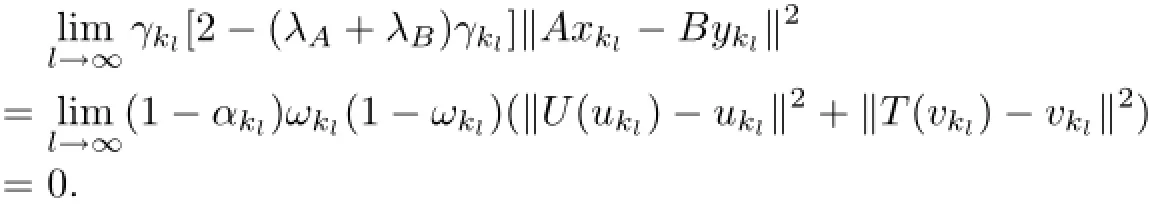
In light of the assumption on γk,αk→o and o<1,we obtain

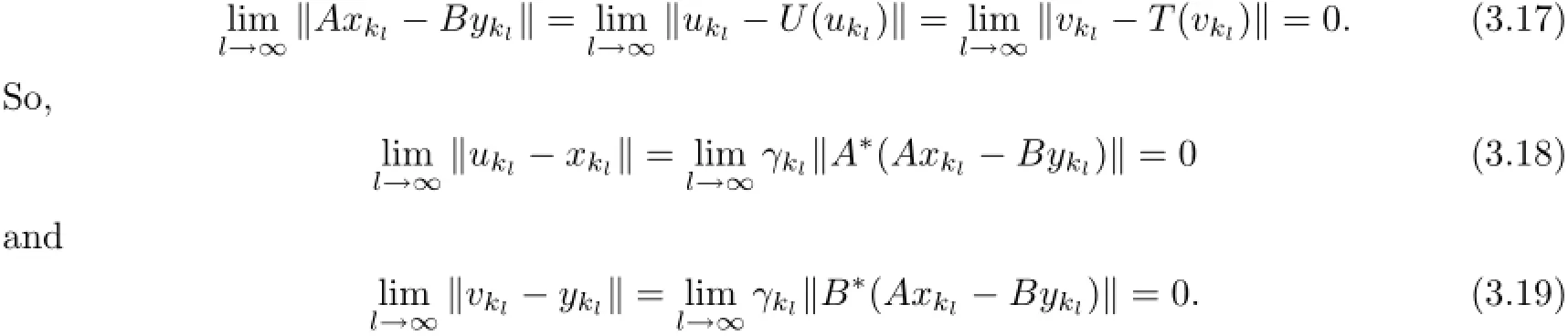
Taking(˜x,˜y)∈ωw(xkl,ykl),from(3.18)and(3.19),we have(˜x,˜y)∈ωw(ukl,vkl).Combined with the demiclosednesses of U−I and T−I at o,(3.17)yields U˜x=˜x and T˜y=˜y.So ˜x∈F(U)and˜y∈F(T).On the other hand,A˜x−B˜y∈ωw(Axkl−Bykl)and weakly lower semicontinuity of the norm imply

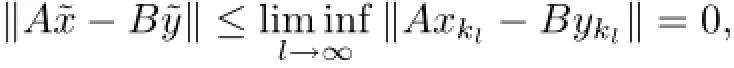
hence(x˜,y˜)∈Γ.So ωw(xkl,ykl)=1−ρ2,to get(3.16),we only need to verify

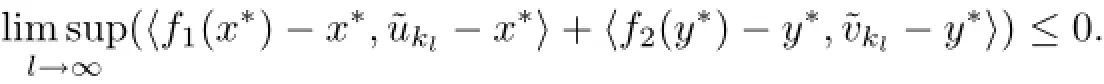
Indeed,from(3.17),(3.18)and(3.19)we have

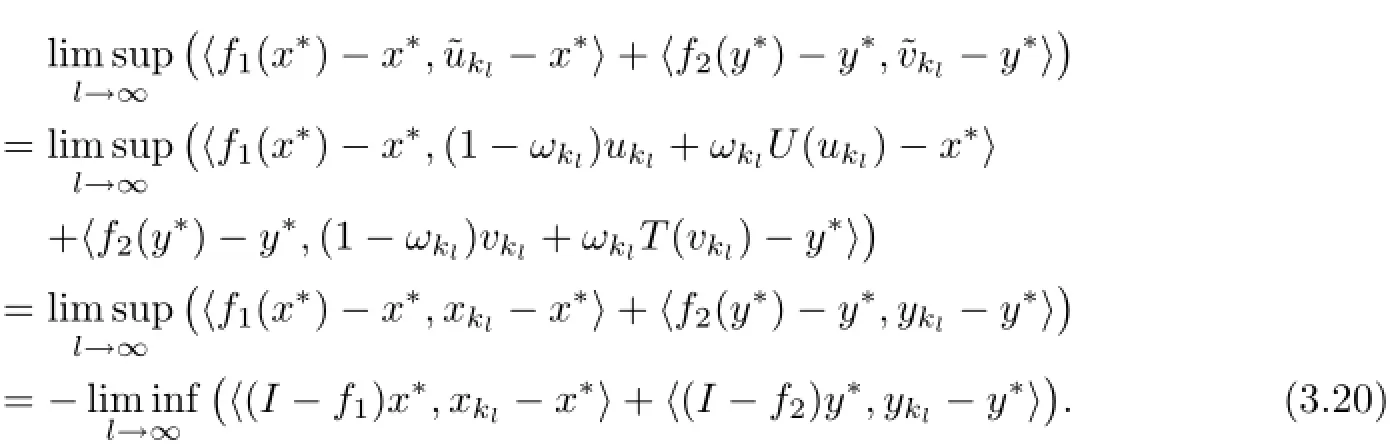
We can take subsequence{(xklj,yklj)}of{(xkl,ykl)}such that(xklj,yklj)⇀(˜x,˜y)as j→∞

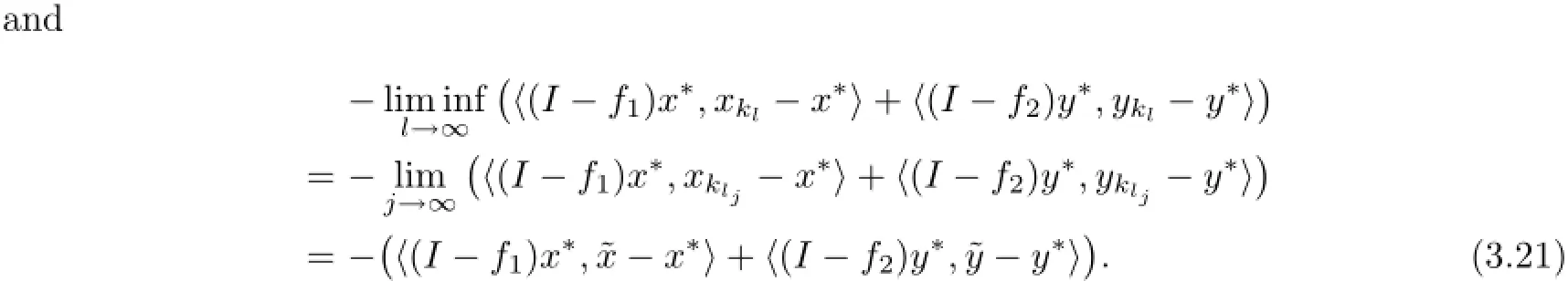
Since ωw(xkl,ykl)⊂Γ and(x∗,y∗)is the solution of the variational inequality problem(3.2), from(3.2o)and(3.21)we obtain

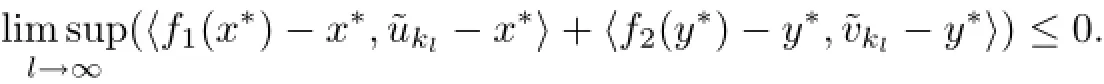
From Lemma 2.6,it follows

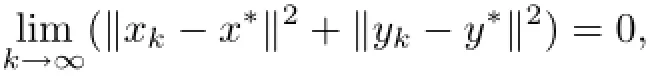
which implies that xk→x∗and yk→y∗.So,the sequence{(xk,yk)}strongly converges to the solution(x∗,y∗)of(1.1)which solves the variational inequality problem(3.2).

Next,we propose another viscosity iterative algorithm for SECFP(1.1)of quasi-nonexpansive operators.

Algorithm 3.3Let f1:H1→H1and f2:H2→H2be two contractions with constants ρ1,ρ2∈[o,1)and αk∈[o,1].Choose initial guesses xo∈H1,yo∈H2arbitrarily.Assume that the kth iterates xk∈H1,yk∈H2have been constructed;then we calculate the(k+1)th iterate(xk+1,yk+1)via the formula

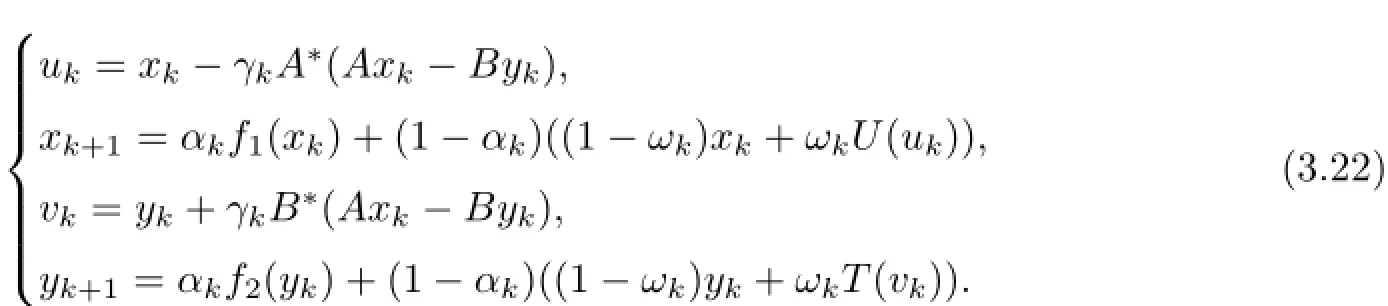
Theorem 3.4Let H1,H2,H3be real Hilbert spaces.Given two bounded linear operators A:H1→H3,B:H2→H3,let U:H1→H1and T:H2→H2be quasi-nonexpansiveoperators with the solution set Γ of(1.1)is nonempty.Assume that the following conditions are satisfied (3)U−I and T−I are demiclosed at origin;

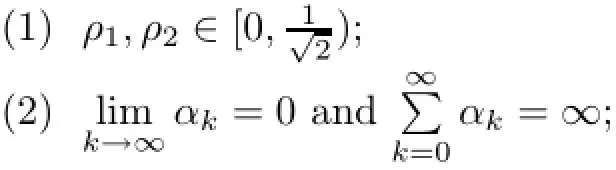
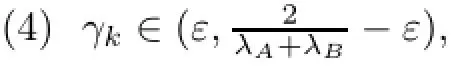
where λA,λBstand for the spectral radius of A∗A and B∗B respectively and ε is small enough;

(5)ωk∈(o,1)such that o

Then the sequence{(xk,yk)}generated by Algorithm 3.3 strongly converges to a solution (x∗,y∗)of(1.1)which solves the variational inequality problem

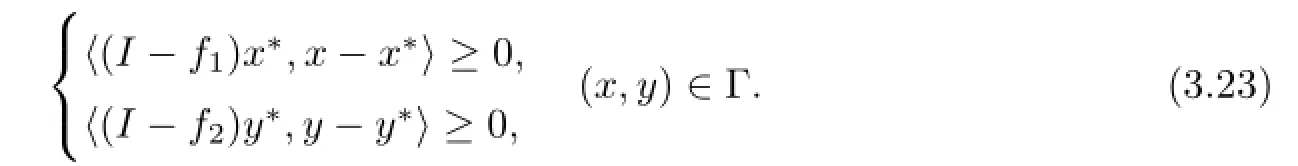
ProofLet(x∗,y∗)∈Γ be the solution of the variational inequality problem(3.23).Then x∗∈F(U),y∗∈F(T)and Ax∗=By∗.By repeating the proof of Theorem 3.2,we have(3.8) and(3.9)is true.

Setting ρ=max{ρ1,ρ2},we have ρ∈By U and T are quasi-nonexpansive operators,it follows from Lemma 2.7 that

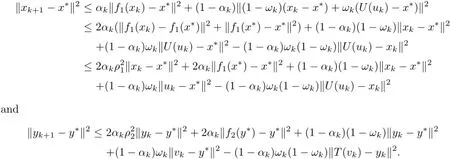
Adding up the last two inequalities and using(3.9),setting sk=‖xk−x∗‖2+‖yk−y∗‖2,we get

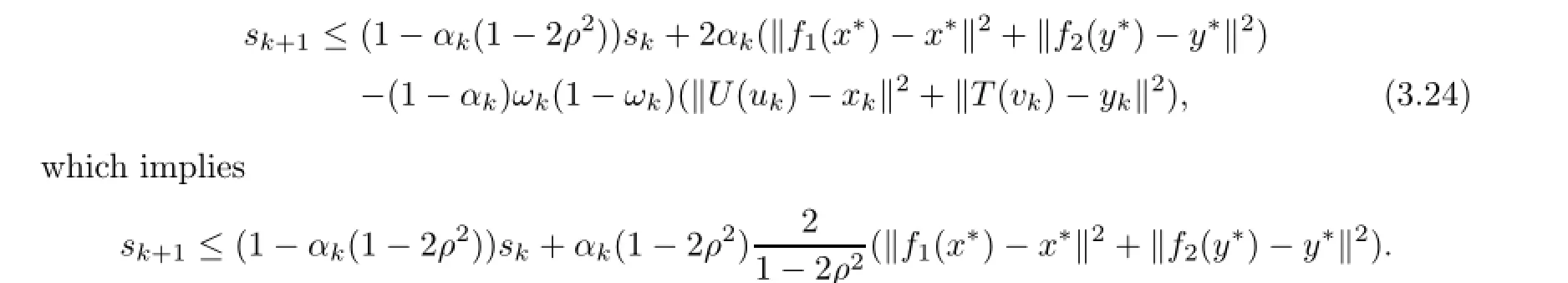
It follows from induction that

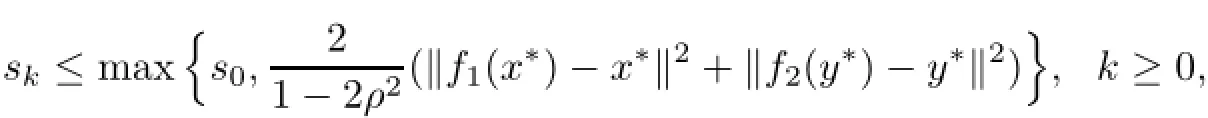
which implies that{xk}and{yk}are bounded.It follows that{uk},{vk},{f1(xk)}and{f2(yk)} are bounded.

Setting¯uk=(1−ωk)xk+ωkU(uk),¯vk=(1−ωk)yk+ωkT(vk),similarly to the proof of Theorem 3.2,we have

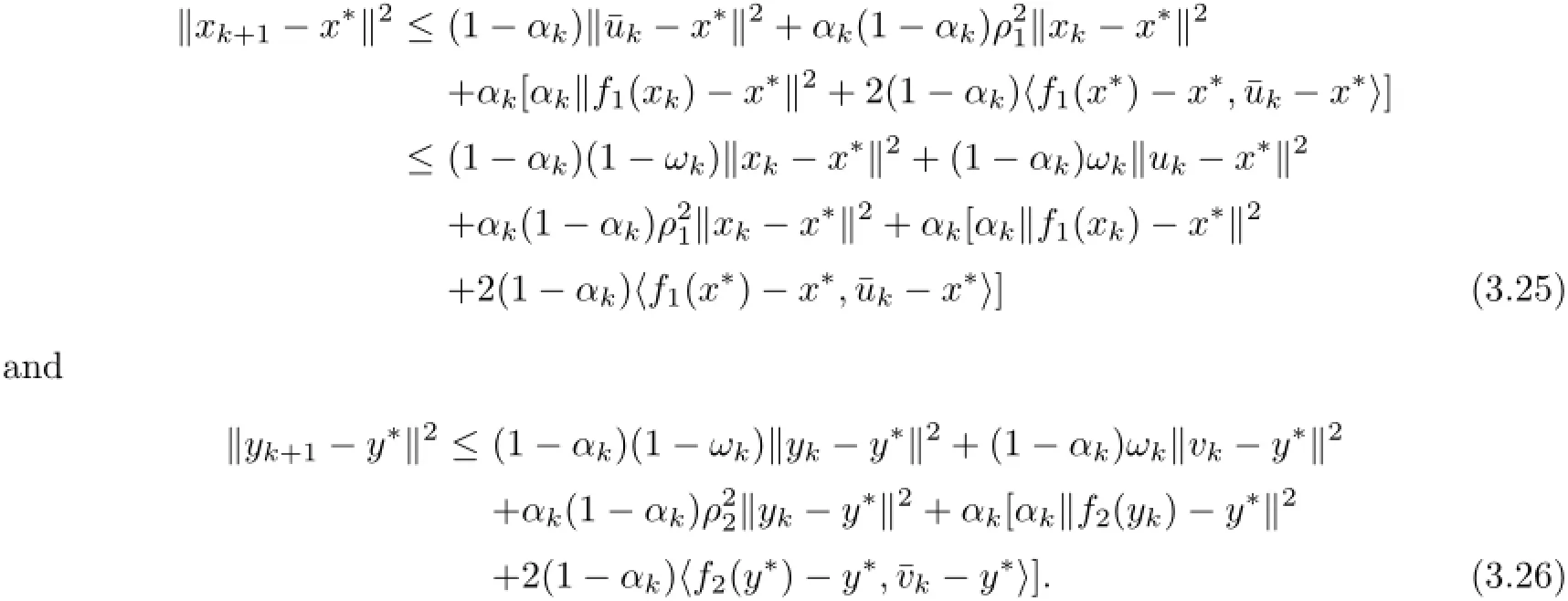
So,by(3.9),(3.25)and(3.26)we obtain

On the other hand,from(3.22),we have

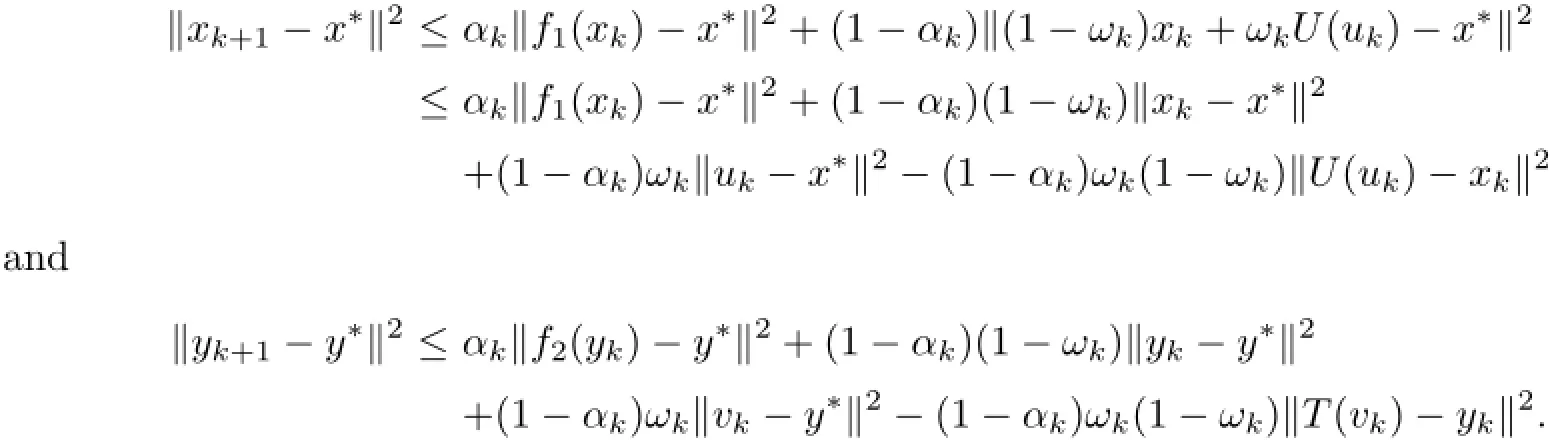
Using(3.8),we obtain

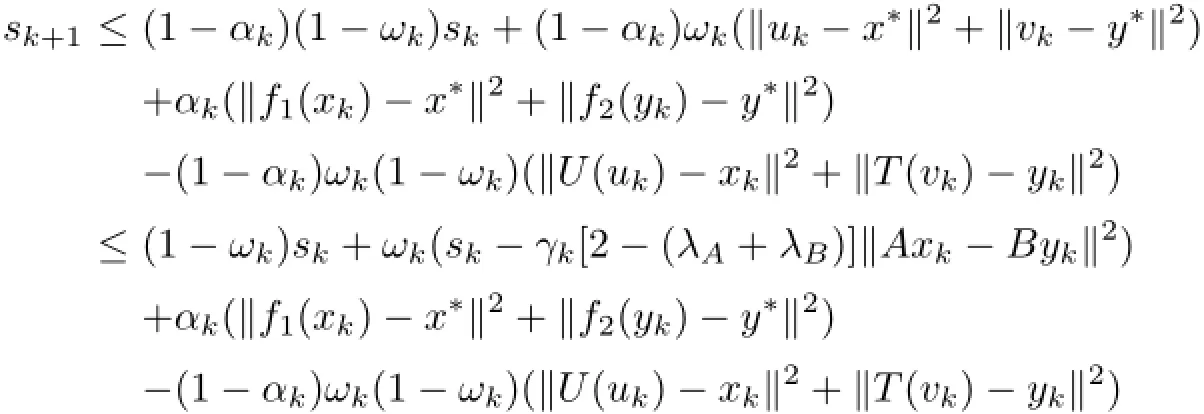
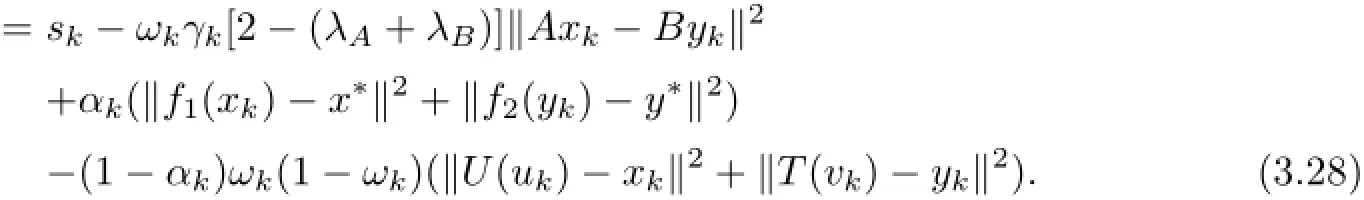
Now,by setting

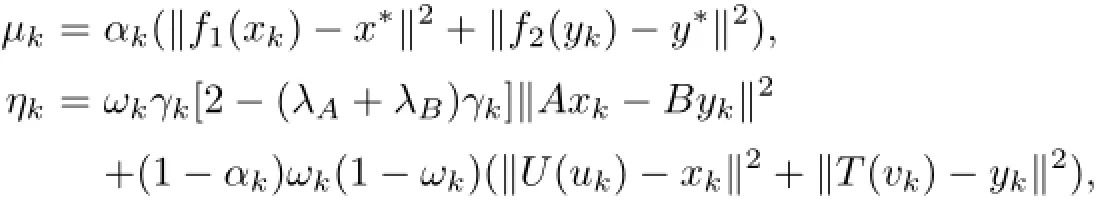
(3.28)can be rewritten as the following form

By the assumption on αk,we get=o which thanks to the boundedness of{xk}and{yk}.

The rest of the proof is analogous to that of Theorem 3.2.

Remark 3.5Recently,Zhao and He[2o]introduced the viscosity approximation algorithm(1.8)with the strong convergence for the SCFP(1.4)of quasi-nonexpansive operators. In[2o],we assumed ρ∈[o,1),

.Similar to the idea of the proof of Theorem 3.4,we can also obtain the strong convergence of the sequence given by(1.8)to the unique solution of the variational inequality problem VIP(I−f, Γ): where ρ∈

References

[1]Byrne C.Iterative oblique projection onto convex subsets and the split feasibility problem.Inverse Problems, 2002,18:441–453

[2]Shehu Y,Mewomo O T,Ogbuisi F U.Further investigation into approximation of a common solution of fixed point problems and split feasibility problems.Acta Math Sci,2016,36B(3):913–930

[3]Byrne C,Censor Y,Gibali A,et al.The split common null point problem.J Nonl Convex Anal,2012,13: 759–775

[4]Censor Y,Gibalin A,Reich S.Algorithms for the split variational inequality problem.Numerical Algorithms,2012,59:301–323

[5]Masad E,Reich S.A note on the multiple-set split convex feasibility problem in Hilbert space.J Nonl Convex Anal,2007,8:367–371

[6]Moudafi A.A note on the split common fixed-point problem for quasi-nonexpansive operators.Nonl Anal Theory Meth Appl,2011,74:4083-4087

[7]Moudafi A.Alternating CQ-algorithm for convex feasibility and split fixed-point problems.J Nonl Convex Anal,2014,15(4):809–818

[8]Attouch H,Bolte J,Redont P,et al.Alternating proximal algorithms for weakly coupled minimization problems.Applications to dynamical games and PDEs.J Convex Anal,2008,15(3):485–506

[9]Censor Y,Bortfeld T,Martin B,et al.A unified approach for inversion problems in intensity-modulated radiation therapy.Physics in Medicine and Biology,2006,51:2353–2365

[10]Censor Y,Elfving T.A multiprojection algorithm using Bregman projections in a product space.Num Algor,1994,8:221–239

[11]Byrne C.A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Problems,2004,20:103–120

[12]Xu HK.A variable Krasnosel’ski˘i-Mann algorithm and the multiple-set split feasibility problem.Inverse Problems,2006,22:2021–2034

[13]Qu B,Xiu N.A note on the CQ algorithm for the split feasibility problem.Inverse Problems,2005,21: 1655–1665

[14]Yang Q.The relaxed CQ algorithm solving the split feasibility problem.Inverse Problems,2004,20:1261–1266

[15]Yang Q,Zhao J.Generalized KM theorems and their applications.Inverse Problems,2006,22:833–844

[16]Bauschke H H,Borwein J M.On projection algorithms for solving convex feasibility problems.SIAM Rev, 1996,38(3):367–426

[17]Xu HK.Iterative methods for the split feasibility problem in infinite-dimensional Hilbert spaces.Inverse Problems,2010,26:105018

[18]Censor Y,Segal A.The split common fixed point problem for directed operators.Journal of Convex Analysis,2009,16:587–600

[19]Moudafi A,Al-Shemas E.Simultaneous iterative methods for split equality problems and application.Tran Math Prog Appl,2013,1:1–11

[20]Zhao J,He S.Strong Convergence of the viscosity approximation process for the split common fixed-point problem of quasi-nonexpansive mappings.J Appl Math,2012,2012:Article ID 438023

[21]He S,Yang C.Solving the variational inequality problem defined on intersection of finite level sets.Abs Appl Anal,2013,2013:Article ID 942315

[22]Matinez-Yanes C,Xu H K.Strong convergence of the CQ method for fixed point processes.Nonlinear Anal-TMA,2006,64:2400–2411

∗October 20,2014;revised October 9,2015.The research was supported by National Natural Science Foundation of China(61503385)and Fundamental Research Funds for the Central Universities of China (3122016L002).†

Jing ZHAO.