EXISTENCE OF SOLUTION AND APPROXIMATE CONTROLLABILITY OF A SECOND-ORDER NEUTRAL STOCHASTIC DIFFERENTIAL EQUATION WITH STATE DEPENDENT DELAY∗
Sanjukta DASDwijendra PANDEYN.SUKAVANAM Department of Mathematics,Indian Institution of Technology Roorkee,Roorkee,Uttarakhand India E-mail:dassanjukta44@gmail.com;dwij.iitk@gmail.com;nsukavanam@gmail.com
EXISTENCE OF SOLUTION AND APPROXIMATE CONTROLLABILITY OF A SECOND-ORDER NEUTRAL STOCHASTIC DIFFERENTIAL EQUATION WITH STATE DEPENDENT DELAY∗
Sanjukta DASDwijendra PANDEYN.SUKAVANAM Department of Mathematics,Indian Institution of Technology Roorkee,Roorkee,Uttarakhand India E-mail:dassanjukta44@gmail.com;dwij.iitk@gmail.com;nsukavanam@gmail.com
This paper has two sections which deals with a second order stochastic neutral partial differential equation with state dependent delay.In the first section the existence and uniqueness of mild solution is obtained by use of measure of non-compactness.In the second section the conditions for approximate controllability are investigated for the distributed second order neutral stochastic differential system with respect to the approximate controllability of the corresponding linear system in a Hilbert space.Our method is an extension of co-author N.Sukavanam’s novel approach in[22].Thereby,we remove the need to assume the invertibility of a controllability operator used by authors in[5],which fails to exist in infinite dimensional spaces if the associated semigroup is compact.Our approach also removes the need to check the invertibility of the controllability Gramian operator and associated limit condition used by the authors in[20],which are practically difficult to verify and apply.An example is provided to illustrate the presented theory.
approximate controllability;cosine family;state dependent delay;neutral stochastic differential equation;measure of noncompactness
2010 MR Subject Classification35R15;35R60;93B05;93E03
1 Introduction
Random noise causes fluctuations in deterministic models.So,necessarily we move from deterministic problems to stochastic ones.Stochastic evolution equations are natural generalizations of ordinary differential equations incorporating the randomness into the equations. Thereby,making the system more realistic.[7–17]and the references therein explore the qualitative properties of solutions for stochastic differential equations.Considering the environmental disturbances,Kolmanovskii and Myshkis[18]introduced a class of neutral stochastic functional differential equations,which are applicable in several fields such as chemical engineering,aeroelasticity and so on.In recent years,controllability of stochastic infinitedimensional systems wasextensively studied for various applications.Several papers studied the approximate controllability of semilinear stochastic control systems,see for instance[5,8,9,19,2o]and references therein.Controllability results are available in overwhelming majority for abstract stochastic differential delay systems;rather than for neutral second-order stochastic differential with state dependent delay.
Mahmudov[2o]investigated conditions on the system operators so that the semilinear control system is approximately controllable provided the corresponding linear system is approximately controllable.The main drawback of the papers[8,19,2o]is the need to check the invertibility of the controllability Gramian operator and a associated limit condition,which are practically difficult to verify and apply.
Neutral differential equations appear in several areas of applied mathematics,and thus studied in several papers and monographs,see for instance[11,12,23]and references therein. Differential equations with delay reflect physical phenomena more realistically than those without delay.
Recently,much attention was paid to partial functional differential equation with state dependent delay.For details see[1,3,13–15].As a matter of fact,in these papers their authors assume severe conditions on the operator family generated by A,which imply that the underlying space X has finite dimension.Thus the equations treated in these works are really ordinary and not partial equations.
Our method builds on co-author Sukavanam’s novel approach in[22].We also remove the need to assume the invertibility of a controllability operator used by authors in[4–6,21]which fails to exist in infinite dimensional spaces if the associated semigroup is compact.Our approach also removes the drawbacks of the method applied in[8,19,2o].
Hence motivated by this fact in this paper we study the existence and uniqueness of mild solution and approximate controllability of the partial neutral stochastic differential equation of second order with state delay.Specifically we study the following second order equations modelled in the form
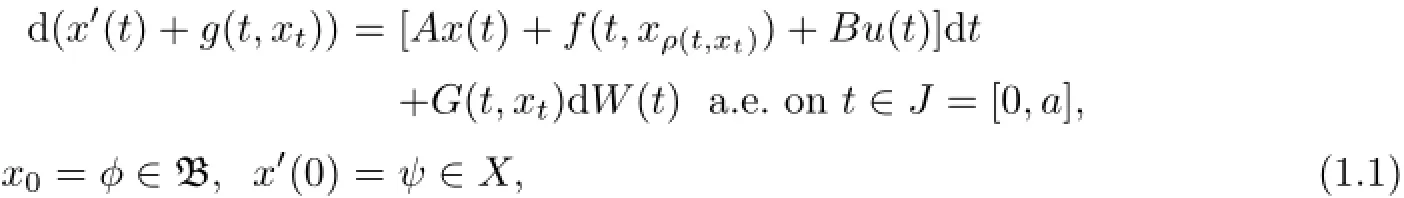
where A is the infinitesimal generator of a strongly continuous cosine family{C(t):t∈R}of bounded linear operators on a Hilbert space X.Let(Ω,F,P)be a probability space together with a normal filtration Ft,t≥o.The state space x(t)∈X and the controlwhere X and U are separable Hilbert spaces and d is the stochastic differentiation.The history valued function xt:(−∞,o]→X,xt(θ)=x(t+θ)belongs to some abstract phase space B defined axiomatically;g,f are appropriate functions;B is a bounded linear operator on a Hilbert space U.Let K be a separable Hilbert space and{W(t)}t≥ois a given K-valued Brownian motion or Wiener process with finite trace nuclear covariance operator Q>o.The functions f,g:J×B→X are measurable mappings in X norm and G:J×B→LQ(K,X) is a measurable mapping in LQ(J,X)norm.LQ(J,X)is the space of all Q-Hilbert Schmidt operators from K into X;B is a bounded linear operator from U into X;φ(t)is B-valued random variable independent of Brownian motion W(t)with finite second moment.Also ψ(t)is a X valued Ftmeasurable function.
2 Preliminaries
In this section some definitions,notations and lemmas that are used throughout this paper are stated.Let(Ω,F,P)be a complete probability space endowed with complete family of right continuous increasing sub σ-algebras{Ft,t∈J}such that Ft⊂F.A X-valued random variable is a F-measurable process.A stochastic process is a collection of random variables S={x(t,w):Ω→X:t∈J}.We usually suppress w and write x(t)instead of x(t,w).
Now suppose βn(t)(n=1,2,···)be a sequence of real-valued one dimensional standard Brownian motions mutually independent over(Ω,F,P).Let ςnbe a complete orthonormal basis in K.Q∈L(K,K)be an operator defined by∞.Let us define
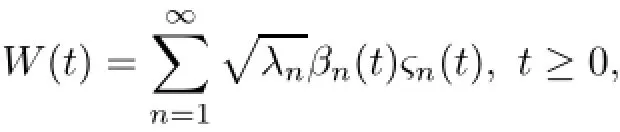
which is a K-valued stochastic process and is called a Q-Wiener process.Let Ft=σ(W(s): o≤s≤t)be the σ-algebra generated by W and Fb=F.Let φ∈L(K,X)and if then φ is called a Q-Hilbert Schmidt operator.The completion LQ(K,X)of L(K,X)with respect to the topology induced by norm‖φ‖2Q=〈φ,φ〉is a Hilbert space.
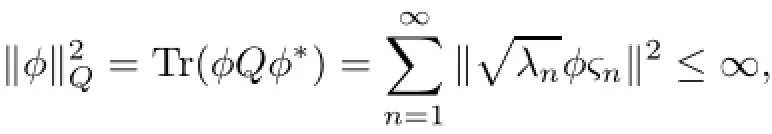
The family{C(t):t∈ℝ}of operators in B(X)is a strongly continuous cosine family if the following are satisfied
(a)C(o)=I(I is the identity operator in X);
(b)C(t+s)+C(t−s)=2C(t)C(s)for all t,s∈ℝ;
(c)the map t→C(t)x is strongly continuous for each x∈X,
{S(t):t∈ℝ}is the strongly continuous sine famRily associated to the strongly continuous cosine family{C(t):t∈ℝ}.It is defined as S(t)x=tC(s)xds,x∈X,t∈ℝ.
o
The operator A is the infinitesimal generator of a strongly continuous cosine function of bounded linear operators(C(t))t∈Rand S(t)is the associated sine function.Let N,Ne be certain constants such that‖C(t)‖≤N and‖S(t)‖≤Ne for every t∈J=[o,a].For more details see books by Goldstein[1]and Fattorini[1o].In this work,we use the axiomatic definition of phase space B,introduced by Hale and Kato[13].
Definition 2.1(see[16])Let B be a linear space of functions mapping(−∞,o]into X endowed with the seminorm‖.‖Band satisfies the following conditions.
(A)If x:(−∞,σ+b]→X,b>o,such that xt∈B and x|[σ,σ+b]∈C([σ,σ+b]:X),then for every t∈[σ,σ+b)the following conditions:
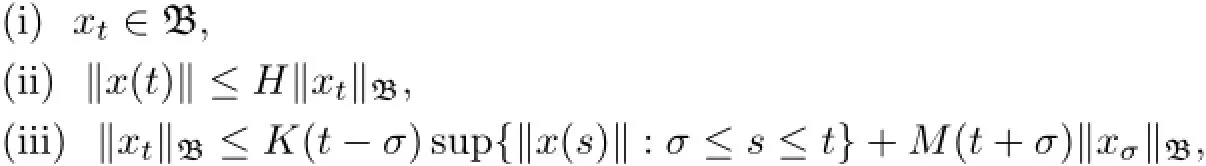
where H>o is a constant K,M:[o,∞)→[1,∞),K is continuous,M is locally bounded and H,K,M are independent of x(·).
(B)The space B is complete.
Lemma 2.2(see[1])If y:(−∞,a]→X is a function such that yo=φ and y|J∈PC(X), then
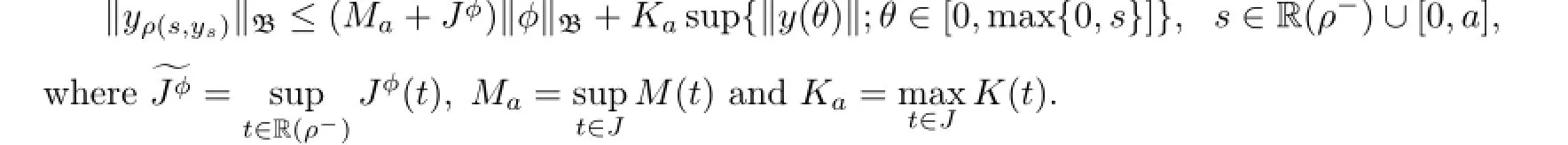
Let us denote E as the expectation defined by E(h)=Ωh(w)dP.
Let L2(Ω,F,P;X)≡L2(Ω;X)be the Banach space of all strongly measurable,square integrable,X-valued random variables equipped with the normL2(Ω;X))denotes the Banach space of all continuous maps from J1=(−∞,a]into L2(Ω;X) which satisimportant subspace.
We denote by C the closed subspace of all continuously differentiable process x∈C1(J, L2(Ω;X))consisting of Ft-adapted measurable processes such thatand semi-.It can be easily seen that C endowed with norm topology is a Banach space.
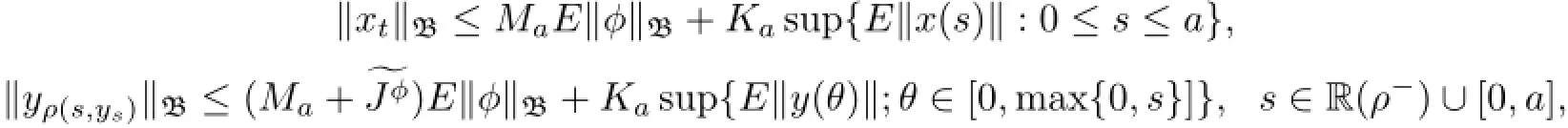
Definition 2.3(see[2])The Hausdorff’s measure of noncompactness χYfor a bounded set B in any Banach space Y is defined by
χY(B)=inf{r>o,B can be covered by finite number of balls with radii r}. Lemma 2.4(see[2])Let Y be a Banach space and B,C⊂Y be bounded,then the following properties hold:
(1)B is pre-compact if and only if χY(B)=o;
(3)χY(B)≤χY(C)when B⊂C;
(4)χY(B+C)≤χY(B)+χY(C)where B+C={x+y;x∈B,y∈C};
(5)χY(B∪C)=max{χY(B),χY(C)};
(6)χY(λB)=‖λ‖χY(B)for any λ∈R;
(7)if the map Q:D(Q)⊂Y→Z is Lipschitz continuous with constant k then χZ(QB)≤kχY(B)for any bounded subset B⊂D(Q),where Z is a Banach space;is a decreasing sequence of bounded closed nonempty subset of Y andis nonempty and compact in Y.
Definition 2.5Let X and Y be Banach spaces and Φ,Ψ be the Measure of Noncompactness(MNC)in X and Y,respectively.If for any continuous function f:D(f)⊂X→Y and any O⊂D(f),Ψ[f(O)]≥Φ(O)implies that O is relatively compact,then f is called (Φ,Ψ)-condensing map.
Theorem 2.6Let Ψ be a MNC on a Banach space X.Let f be(Ψ,Ψ)condensing operator.If f maps a nonempty,convex,closed subset M of the Banach space X into itself. Then f has atleast one fixed point in M.
Definition 2.7The set given by R(f)={x(T)∈X:x is a mild solution of(1.1)}is called reachable set of system(1.1)for some T>o.R(o)is the reachable set of the corresponding linear control system(2.1).
Definition 2.8System(1.1)is said to be approximately controllable if R(f)is dense in X.The corresponding linear system is approximately controllable if R(o)is dense in X.
Lemma 2.9(see[22])Let X be Hilbert space and X1,X2closed subspaces such that X=X1+X2.Then there exists a bounded linear operator P:X→X2such that for each x∈X,x=x−Px∈X1and‖x1‖=min{‖y‖:y∈X1,(1−Q)(y)=(1−Q)(x)},where Q denotes the orthogonal projection on X2.
We state the corresponding linear control system

Lemma 2.10(see[1o])Under the assumption that h:[o,a]→X is an integrable function,such that
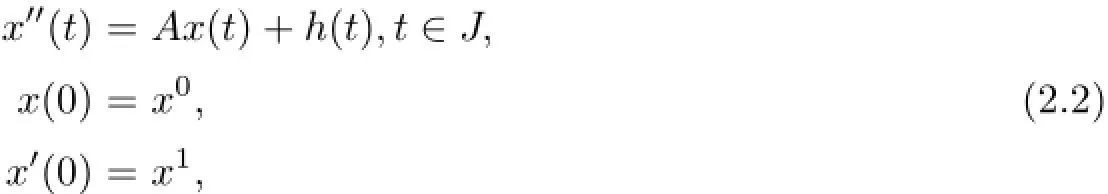
and h is a function continuously differentiable,then
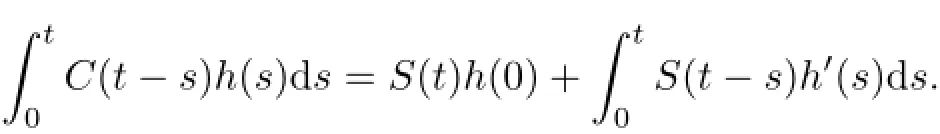
3 Main Result
We define mild solution of problem(1.1)as follows.
Definition 3.1An Ft-adapted process x:(−∞,a]→X is a mild solution of problem (1.1),if xo=φ,x′(o)=ψ,x(.)∈C1(J,L2(Ω,X)),the functions f(s,xρ(s,xs)),G(s,xs)and g(s,xs)are integrable and the integral equation is satisfied
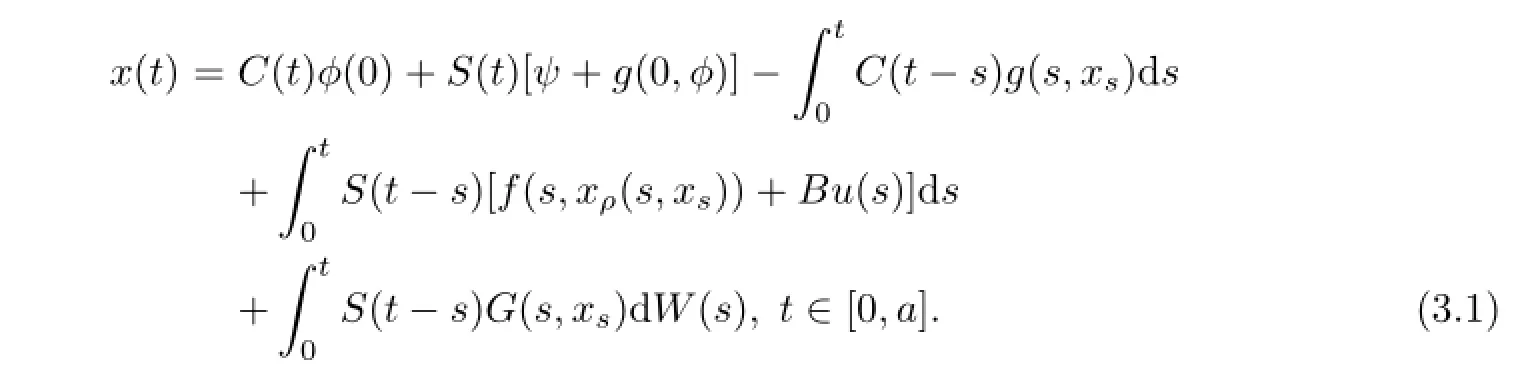
To prove our result we always assume ρ:J×B→(−∞,a]is a continuous function.The following hypotheses are used.
(Hφ)The function t→φtis continuous from ℝ(ρ−)={ρ(s,ψ):ρ(s,ψ)≤o}into B and there exists a continuous bounded function Jφ:ℝ(ρ−)→(o,∞)such that‖φt‖B≤Jφ(t)‖φ‖Bfor every t∈ℝ(ρ−).
(Hf)f:J×B→X satisfies the following.
(1)For every x:(−∞,a]→X,xo∈B and x|J∈PC,the function f(.,ψ):J→X is strongly measurable for every ψ∈B and f(.,t)is continuous for a.e.t∈J.
(2)There exists an integrable function α:J→[o,+∞)and a monotone continuous nondecreasing function Υf:[o,+∞)→(o,+∞)such that‖f(t,v)‖≤α(t)Υf(‖v‖B)∀t∈J and v∈B.
(HG)The function G satisfies the following conditions.
(1)For almost all t∈J the function G(t,.):B→LQ(K,X)is continuous.For all z∈B, the function G(.,z):J→LQ(K,X)is strongly Ftmeasurable.
(2)∃integrable function αG:J→[o,∞)and a monotone continuous nondecreasing function ΥG:[o,∞)→(o,∞)such that

(Hg)The function g(.)is continuous∀(t,v)∈J×B and g(t,.)is Lipschitz continuous such that there exists a positive constant Lgsuch that

(Hl)There exists a function H:[o,∞)×[o,∞)→[o,∞),which is locally integrable in t, H is a continuous,monotone,nondecreasing in second variable and H(t,o)≡o and
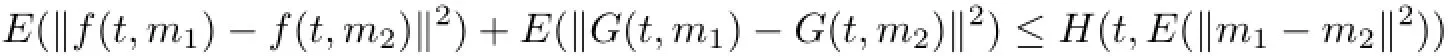
for all t∈[o,a]and m1,m2∈L2(Ω,F,X).
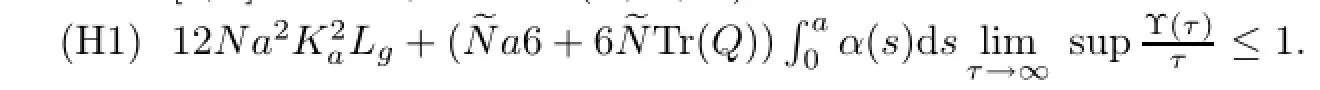
Lemma 3.2(see[2])Let m be a nonnegative,continuous function and A>o such that
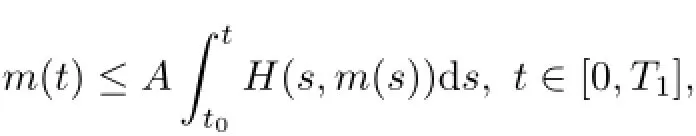
then m has no nonzero nonnegative solution.
3.1Existence and Uniqueness of Mild Solution
In this section y:(−∞,a]→X is the function defined by yo=φ and y(t)=C(t)φ(o)+o≤s≤a}.
Theorem 3.3If hypotheses(Hf),(Hg),(Hφ),(HG),(H1)and(Hl)are satisfied,then the initial value problem(1.1)has atleast one mild solution.
ProofLet S(a)be the space S(a)={x∈C(J,L2(Ω;X):x(o)=o}endowed with the norm of uniform convergence;x∈Cois identified with its extension to(−∞,a]by assuming x(θ)=o for θ Let Γ:S(a)→S(a)be the map defined by Thus Γ is well defined and has values in S(a).Also by axioms of phase space,the Lebesgue dominated convergence theorem,and conditions(Hf),(HG),(Hg)it can be shown that Γ is continuous. Step 1We prove that there exists k>o such that Γ(Bk)⊂Bk,where Bk={x∈S(a): E‖x‖2≤k}.In fact,if we assume that the assertion is false,then for k>o,there exist xk∈Bkand t∈(o,a]such that k<‖E(Γxk(tk))‖2, where Υ=max{ΥG,Υf},α=max{αf,αG}.Thus(3.4)is a contradiction to hypothesis(H1). Hence Γ(Bk)⊂Bk. Step 2We prove that Γ is a condensing map on any bounded subset of the space C(J,L2(Ω;X)).Let O be a bounded subset of C(J,L2(Ω;X)).Let M[o,a]be the partially ordered linear space of all real monotone nondecreasing functions on[o,a]and we define a Measure of Noncompactness(MNC),Ψ:C(J,L2(Ω;X))→M[o,a]by where χtis the Hausdorff MNC in C(J,L2(Ω;X))and Ot={xt=x|[o,t]:x∈O}⊂C([o,t],L2(Ω;X)).If Ψ(O)≤Ψ(ΓO),then it is proved that Ψ(O)=o.Since the function t→[Ψ(O)](t)is nondecreasing and bounded,so∀∊>o,it has only a finite number of jumps of magnitude greater than∊.The disjoint δ1neighborhoods of the points corresponding tothese jumps are removed from[o,a].Using points βj,j=1,2,···,m divide the remaining part into intervals on which the oscillations of Ψ(O)is less than∊.These points βjare surrounded by disjoint δ2neighborhoods.Now consider the family o={ok:k=1,···,l}of all functions continuous with probability one,such that okcoincides with an arbitrary element of [(Ψ(O))(βj)+1]net of the set Oβjon the segment σj=[βj−1+δ2,βj−δ2],j=1,···,m and linear on the complementary segments. Suppose p∈(ΓO)t.This implies p=Γo for some o∈O andThis implies that for s∈σj, By choosing δ1>o and δ2>o sufficiently small,we can make sure that Together with Lemma 3.2,we get that Ψ(O)≡o.Similarly we can prove that Γ is continuous. The MNC Ψ possess all required properties.The operator Γ is condensing.Then from Theorem 2.6,it is implied that there exist a mild solution to problem(1.1). The uniqueness of mild solution follows from Lemma 3.2.Let m1,m2∈C(J,L2(Ω;X))be two mild solution of Γ.Then it follows that Thus from Lemma 3.2,it follows that≡o.Hence m1=m2. 3.2Approximate Controllability In this section the approximate controllability of the distributed control system(1.1)is studied as an extension of co-author Sukavanam’s method in[22].Assume that f,g,G satisfy following conditions. (C1)The function f,g:J×B→X are continuous.For all t∈J and∀z1,z2∈L2(J;B), there exists constants Lf,Lg>o such that (C2)The function G:J×B→LQ(K,X)is Lipschitz continuous with constant LG>o such that Also,y:(−∞,a]→X is the function defined by yo=φ and y(t)=C(t)φ(o)+S(t)(z+g(o,φ) on J.Clearly The operators Λi:L2(J,X)→X,i=1,2 and Λ3:L2(J,X)→Co(J,L2(Ω,(LQ(K,X)))) are defined as Clearly Λiare bounded linear operators.We set Ni=ker(Λi),Λ=(Λ1,Λ2,Λ3)and N= ker(Λ).Let Co(J,X)denote the space consisting of continuous functions x:J→X such that x(o)=o,endowed with the norm of uniform convergence.Let Ji:L2(J,X)→Co(J,X),i= 1,2 and J3:L2(J,X)→Co(J,L (Ω,L(K,X)))be maps defined as follows So,Jix(a)=Λi(x),i=1,2.For a fixed φ∈B and x∈C(J,X)such that x(o)=φ(o),we define maps F,g:Co(J,X)→L2(J,X)by F(z)(t)=f(t,zt+xt)and g(z)(t)=g(t,zt+xt).We also define maps G(z)(t)=G(t,zt+xt),here xt(θ)=x(t+θ),for t+θ≥o and xt(θ)=φ(t+θ) for t+θ≤o and zt(θ)=z(t+θ)for t+θ≥o and zt(θ)=o for t+θ≤o.Clearly,F,g,G are continuous maps.We also assume thatWe denote Pi,i=1,2,3 the map associated to this decomposition and construct X2=Ni,i=1,2,3 andWe introduce the space Lemma 3.4If hypothesis(Hφ)–(Hg)and conditions(C1)–(C2)hold for f,g,G and aKa(c1NeLf+c2NLg) is a contraction for n sufficiently large and therefore Γ has a fixed point. Theorem 3.5If the associated linear control system(2.1)is approximately controllableand condition of the preceding lemma hold then the semilinear control system with state dependent delay is approximately controllable on J. ProofAssume x(.)to be the mild solution and u(.)to be an admissible control function of system(2.1)with initial conditions x(o)=φ(o)and x′(o)=ψ+g(o,φ).Let z be the fixed point of Γ.So,z(o)=o and z(a)=Λ1(P1(F(z)))−Λ2(P2(g(z)))+Λ3(P3(G(z)))=o.ByLemma 2.9,we can split the functions F(z),g(z)with respect to the decomposition L2(J,X)= We define the function y(t)=z(t)+x(t)for t∈J and yo=φ.So,x(a)=y(a).Thus by the properties of x and z, As C1(J,L2(Ω,U))is dense inand aBy Lemma 2.1o,we get Hence by Definition 2.8 and the last expression we conclude that ynis the mild solution of the following equation Hence yn(a)∈R(a,f,g,G,φ,ψ).Since the solution map is generally continuous,yn→y as In this section,we discuss a concrete partial differential equation applying the abstract results of this paper.In this application,B is the phase space Co×L2(h,X),see[11]. Consider the second order neutral differential equation where φ∈Co×L2(h,X),o system(4.1)can be transformed into system(1.1).Assume that the functions ρi:ℝ→[o,∞), a:ℝ→ℝ are piecewise continuous. Moreover g(t,·)is bounded linear operators. Hence by assumptions(a)–(c)and Theorem 3.3,it is ensured that problem(4.1)has a unique mild solution. Now,we check the approximate controllability of(4.1).and Ayeigenfunction corresponding to the eigenvaluebase;A will generate the operators S(t),C(t)such that1,2,···,∀y∈X,and the operatorthe infinite dimensional control space be definedThe bounded linear operator B:L2([o,T];U)→L2([o,T];X)is defined by(Bu)(t)=eBu(t). Let a∈N⊂L(o,T:X),N is the null space of Γ. The Hilbert space L2(o,T)can be written as Thus for h1,h2∈L2(o,T),there exists a1∈{sins}⊥,a2∈{sin4s}⊥such that h1−2h2= a1−2a2.So let u2=h2−a2.Then h1=a1+2u2,h2=a2+u2also let un=hn,n=3,4,··· and an=o,n=3,4,···.Thus we see that hypothesis(HR)is satisfied as U={u:u=controllability is deduced from Theorem 3.5. [1]Ahmad B.Instability of impulsive hybrid state dependent delay differential systems.Vietnam J Math,2007, 35:285–298 [2]Akhmerov R,Kamenskii M,Potapov A,Rodkina A,Sadovskii B.Measures of Noncompactness and Condensing Perators.Basel,Boston,Berlin:Birkhauser-Verlag [3]Anguraj A,Arjunan M M,Hernndez E.Existence results for an impulsive neutral functional differential equation with state-dependent delay.Appl Anal,2007,86:861–872 [4]Balachandran K,Park J Y.Existence of solutions and controllability of nonlinear integrodifferential systems in Banach spaces.Math Probl Eng,2003,2:65–79 [5]Balasubramaniam P,Dauer J P.Controllability of semilinear stochastic delay evolution equations in Hilbert spaces.Int J Math Math Sci,2002,31(3):157–166 [6]Balasubramaniam P,Park J,Muthukumar P.Approximate controllability of neutral stochastic functional differential systems with infinite delay.Stoch Anal Appl,2010,28(2):389–400 [7]Bao H,Cao J.Existence and uniqueness of solutions to neutral stochastic functional differential equations with infinite delay.Appl Math Comput,2009,215:1732–1743 [8]Dauer J,Mahmudov N.Controllability of stochastic semilinear functional differential equations in Hilbert spaces.J Math Anal Appl,2004,290:373–394 [9]Ehrhard M,Kliemann W.Controllability of stochastic linear systems.Syst Control Lett,1982,2:145–153 [10]Fattorini H O.Second Order Linear Differential Equations in Banach Spaces.North-Holland Math Stud 108.Amsterdam:North-Holland,1985 [11]Hern´andez E.Existence results for partial neutral integrodifferential equations with unbounded delay.J Math Anal Appl,2004,292:194–210 [12]Hern´andez E,Henr´ıquez H.Existence results for partial neutral functional differential equation with unbounded delay.J Math Anal Appl,1998,22:452–475 [13]Hern´andez E,McKibben M.On state-dependent delay partial neutral functional-differential equations. Appl Math Comput,2007,186:294–301 [14]Hern´andez E,Rabello M,Henr´ıquez H R.Existence of solutions for impulsive partial neutral functional differential equations.J Math Anal Appl,2007,331:1135–1158 [15]Hern´andez E,Sakthivel R,Aki S T.Existence results for impulsive evolution differential equations with state-dependent delay.Elec J Differ Equ,2008,28:1–11 [16]Hale J K,Kato J.Phase space for retarded equations with infinite delay.Funkcial Ekvac,1978,21:11–41 [17]Jankovic S,Randjelovi J,Jovanovi M.Razumikhin-type exponential stability criteria of neutral stochastic functional differential equations.Math Anal Appl,2009,355:811–820 [18]Kolmanovskii V,Myshkis A.Applied Theory of Functional Differential Equations.Norwell,MA:Kluwer Academic Publishers,1992 [19]Mahmudov N.Controllability of linear stochastic systems.IEEE Trans Autom Control,2001,46:724–731 [20]Mahmudov N,McKibben M.Approximate controllability of second-order neutral stochastic evolution equations.Dyn Cont,Discr Impul Syst Series B:Appl Algor,2006,13:619–634 [21]Park J,Balasubramaniam P,Kumaresan N.Controllability for neutral stochastic functional integrodifferential infinite delay systems in abstract space.Numer Funct Anal Optim,2007,28:1–18 [22]Sukavanam N.Approximate controllability of semilinear control of control system with growing nonlinearity//Math Theory of Control Proc Int Conf.New York:Marcel Dekker,1993:353–357 [23]Wang L.Approximate controllability of delayed semilinear control of control system.J Appl Math Stoch Anal,2005,1:67–76 ∗June 23,2014;revised April 25,2016.The was supported by Ministry of Human Resource and Development(MHR-02-23-200-429/304). AcknowledgementsThe would like to thank Ministry of Human Resource and Development with grant no.MHR-o2-23-2oo-429/3o4 for their funding.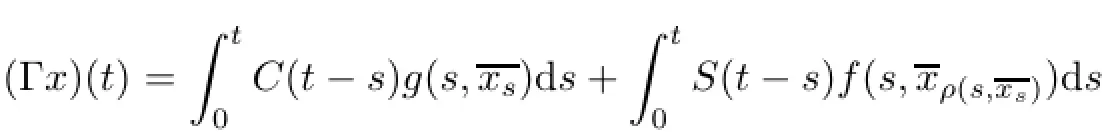

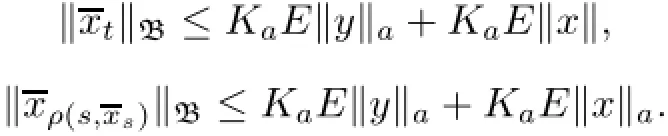

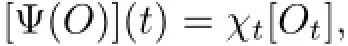


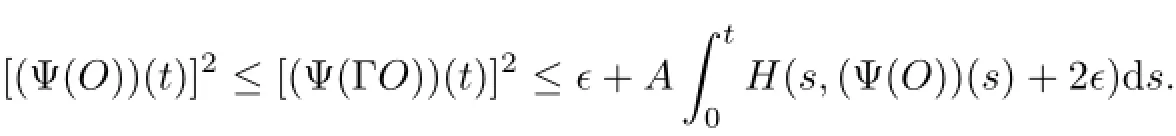
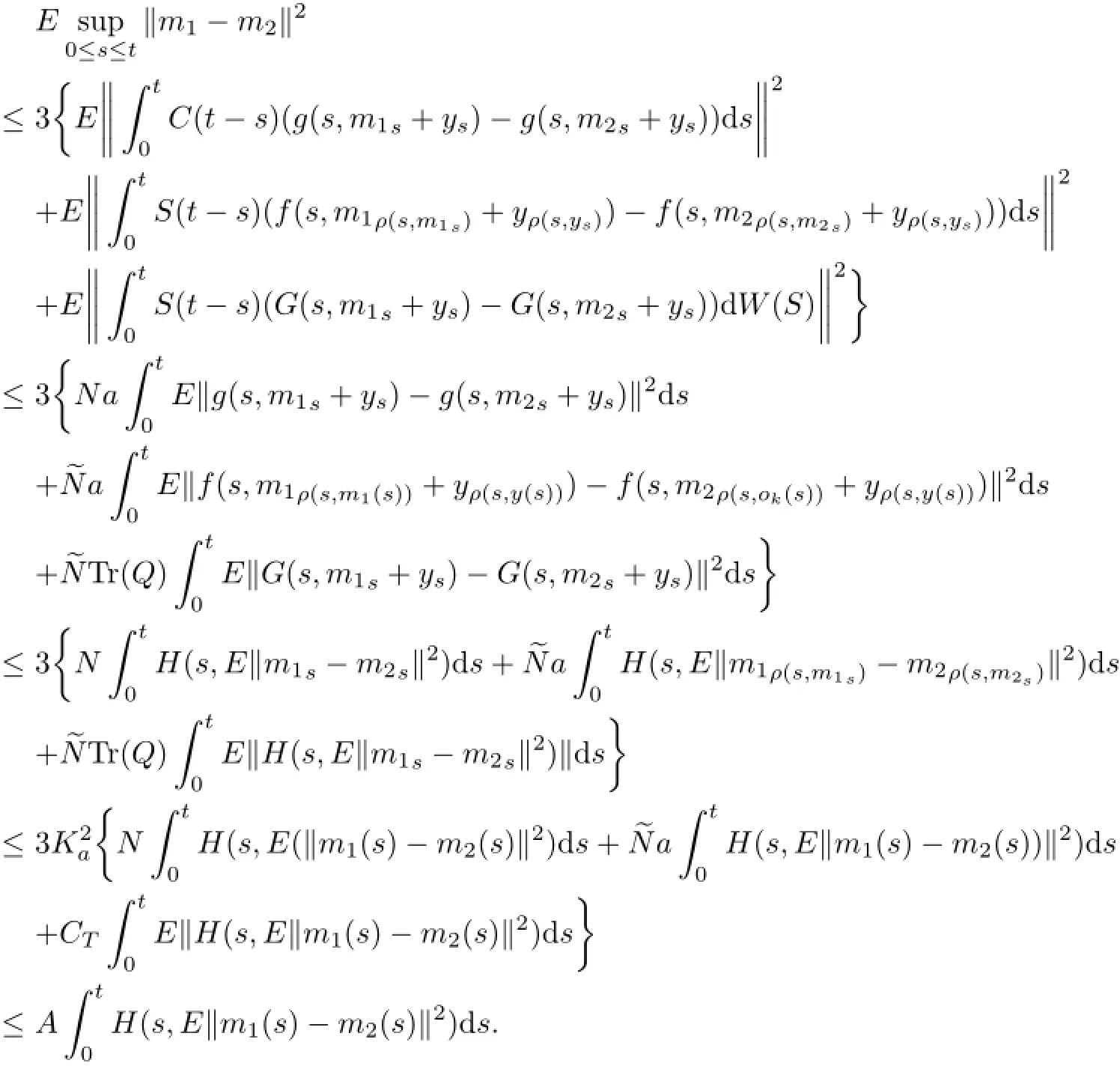
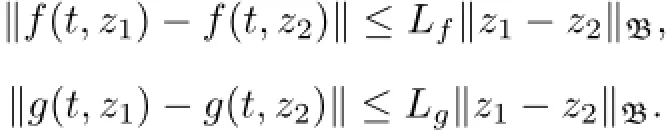
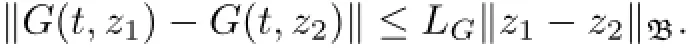
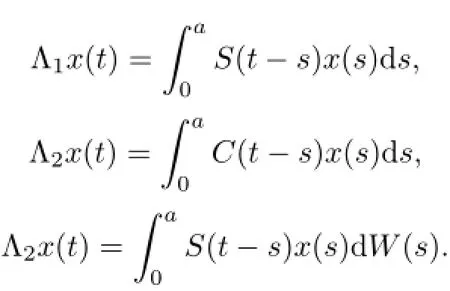
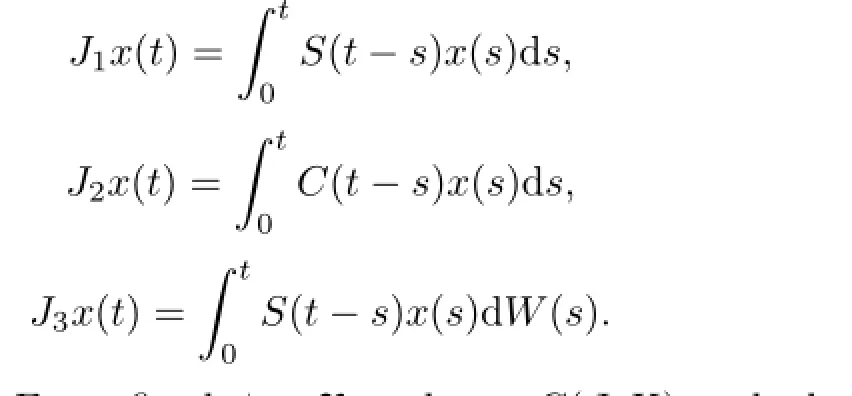
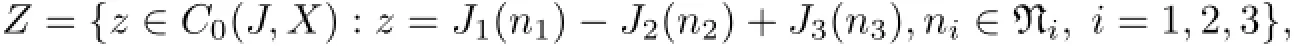
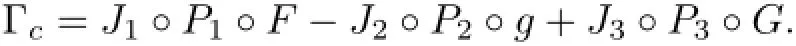


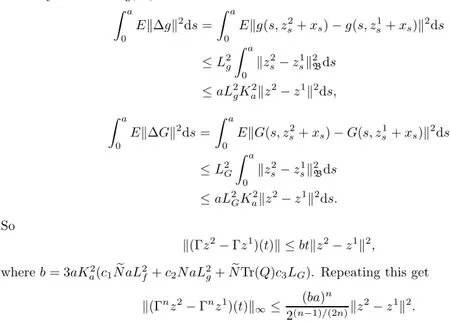

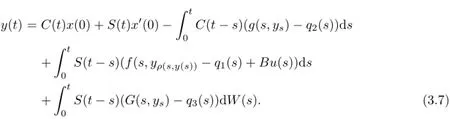
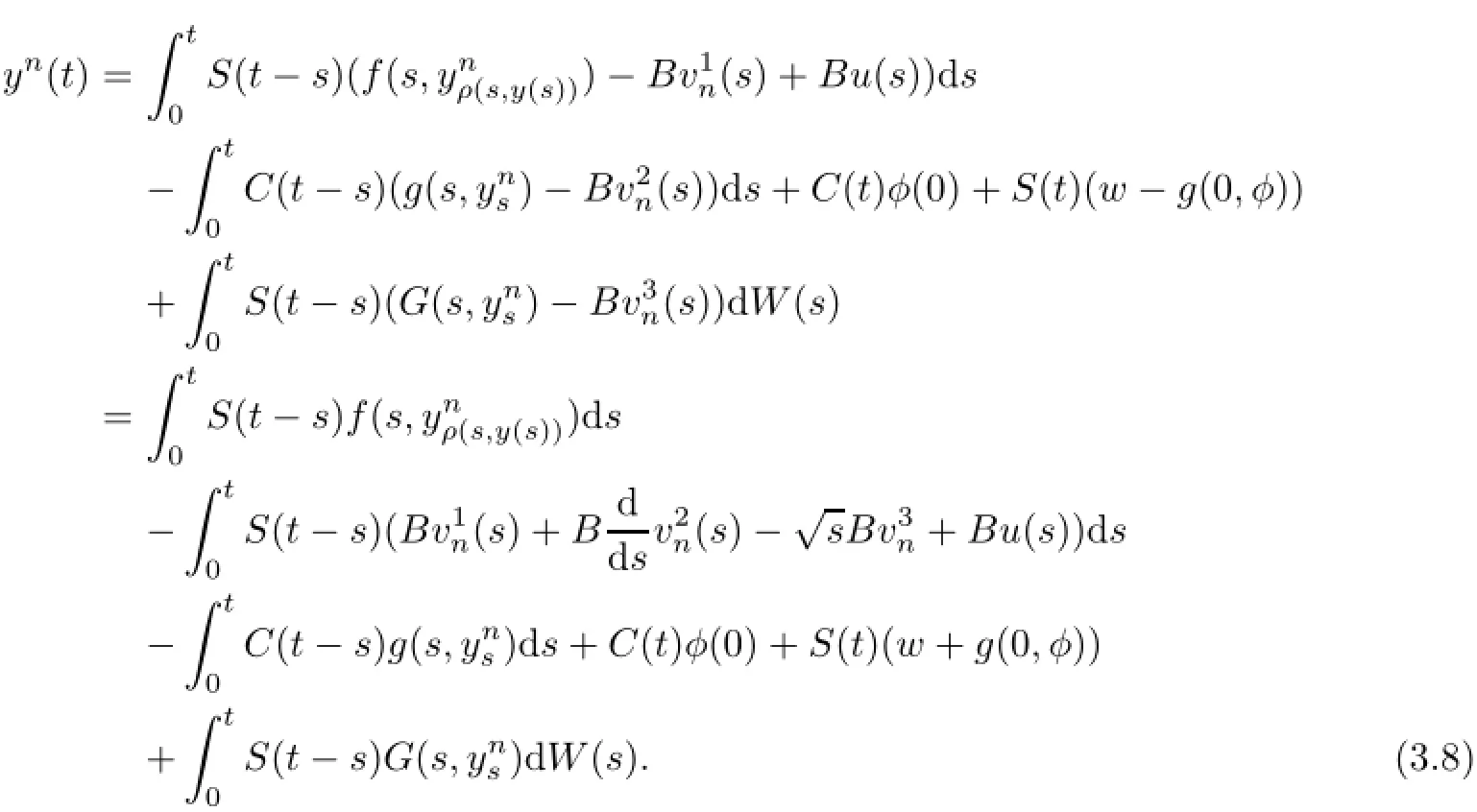

4 Example
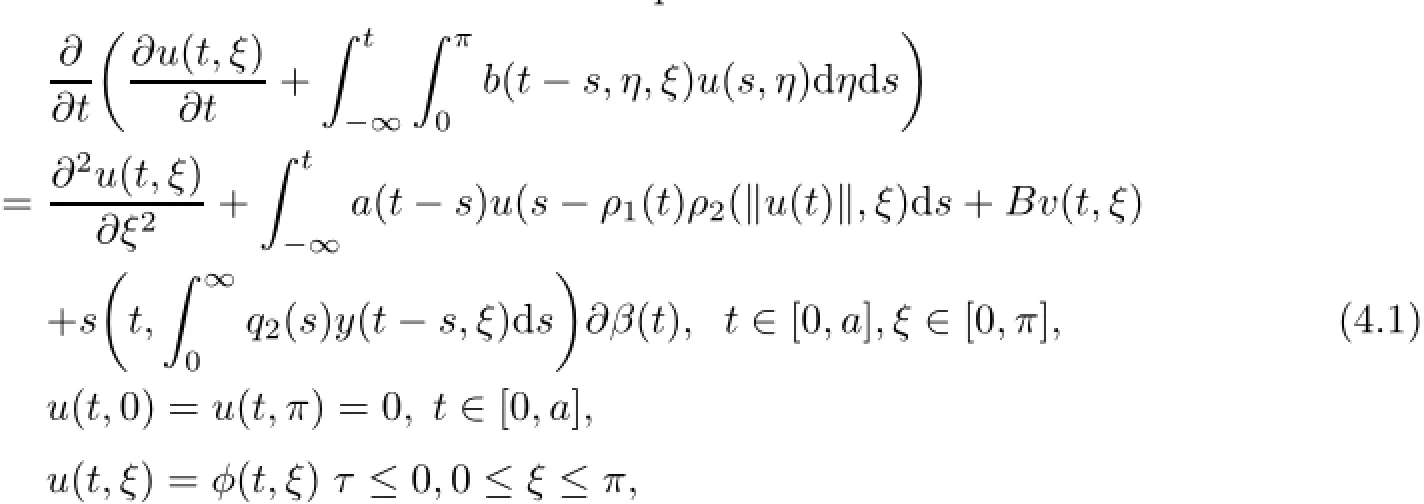
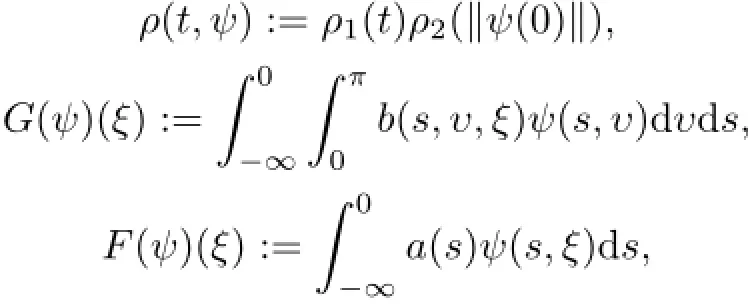
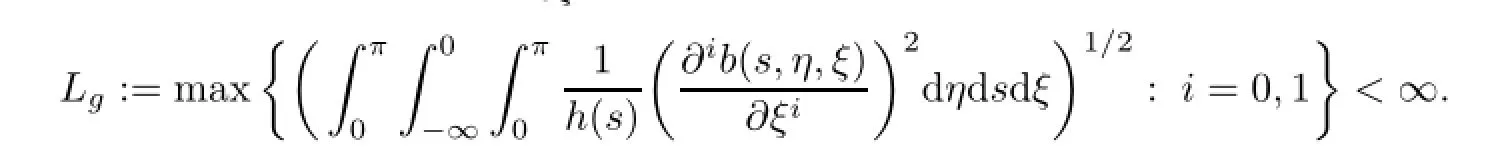
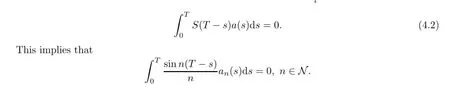
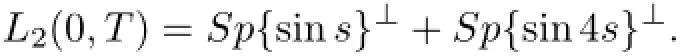
References
 Acta Mathematica Scientia(English Series)2016年5期
Acta Mathematica Scientia(English Series)2016年5期
