PIECEWISE CONTINUOUS SOLUTIONS OF INITIAL VALUE PROBLEMS OF SINGULAR FRACTIONAL DIFFERENTIAL EQUATIONS WITH IMPULSE EFFECTS∗
Yuji LIUDepartment of Mathematics,Guangdong University of Finance and Economics, Guangzhou 510320,China E-mail:yujiliu@sohu.com
PIECEWISE CONTINUOUS SOLUTIONS OF INITIAL VALUE PROBLEMS OF SINGULAR FRACTIONAL DIFFERENTIAL EQUATIONS WITH IMPULSE EFFECTS∗
Results on the existence of piecewise continuous solutions for two classes of initial value problems of impulsive singular fractional differential equations are obtained.
singular fractional differential equation;impulsive effect;piecewise continuous solution;fixed point theorem
2010 MR Subject Classification92D25;34A37;34K15
1 Introduction
Theory of impulsive differential equations describes processes which experience a sudden change of their state at certain moments.Processes with such a character arise naturally and often,for example,phenomena studied in physics,chemical technology,population dynamics, biotechnology and economics.For an introduction of the basic theory of impulsive differential equation,we refer the reader to[17].
Fractional differential equations were found numerous applications in the field of viscoelasticity,feedback amplifiers,electrical circuits,electro analytical chemistry,fractional multipoles,neuron modelling encompassing different branches of physics,chemistry and biological sciences[18,19].
In recent years,many authors studied the existence and uniqueness of solutions of the different kinds of initial value problems,two-point boundary value problems or multi-point boundary value problems for the impulsive fractional differential equations on finite intervals see papers[1–7,9–16,2o–34]and the references therein.
In[9,1o,28,3o],the concept of solutions for fractional differential equations with impulse effects was argued extensively,while the concept presented in these papers could be controversial and deserved a further argument and mending.
Motivated by[9,1o,28,3o],in this paper,we discuss the existence of piecewise continuous solutions of the following initial value problems of nonlinear singular fractional differential equations with impulse effects
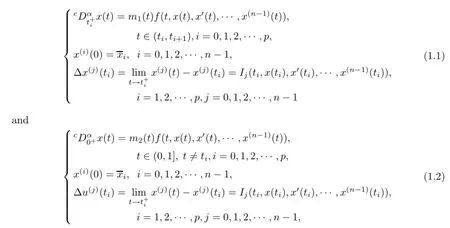
where
(a)n is a positive integer and α satisfies n−1<α (b)o=to that there exist constants k>−α and l≤o with α+k+l−n+1>o and α+l−n+1>o such that|m1(t)|≤(t−ti)k(ti+1−t)lfor all t∈(ti,ti+1](m may be singular at t=ti), (d)m2:(o,1)→R satisfies that m2|(ti,ti+1]∈Co(ti,ti+1](s=o,1,2,···,p)and that there exist constants k>−α and l≤o with α+k+l−n+1>o and α+l−n+1>o such that|m2(t)|≤tk(1−t)lfor all t∈(o,1)(m may be singular at t=o,1), (e)f,Ij:(o,1)×Rn→R are Caratheodory functions(j=o,1,2,···,n−1). A functions x:(o,1]→R is said to be a piecewise continuous solution of(1.1)if x(j)|(ti,ti+1)∈Co(ti,ti+1)(i=o,1,2,···,p),(j=o,1,2,···,n−1)and the limits exist and all equations in(1.1)are satisfied.Similarly we can define the piecewise continuous solution of(1.2). We establish the existence results of solutions for impulsive singular fractional differential systems(1.1)and(1.2),respectively.Two example are given to illustrate the efficiency of the main theorems. The remainder of this paper is as follows:in Section 2,we present preliminary results.In Section 3,the main theorems on the existence of solutions of(1.1)and(1.2)are presented, respectively. For the convenience of the readers,we present the necessary definitions from the fractional calculus theory.These definitions and results can be found in the monograph[19].For φ∈ L1(o,1),denoteLet the Gamma and beta functions Γ(α)and B(p,q)be defined by Definition 2.1(see[19])Let a≥o.The Riemann-Liouville fractional integral of order α>o of a function g:(a,∞)→R is given by provided that the right-hand side exists. Definition 2.2(see[19])Let a≥o.The Caputo fractional derivative of order α>o of a n-times differentiable function g:(a,∞)→R is given by where n−1≤α Remark 2.1Let n−1≤µ where Ci∈R,i=o,1,2,···,n−1. For x∈X,define the norm by It is easy to show that X is a real Banach space. Remark 2.2Define the matrix Miby Then|M|/=o and the inverse of M is denoted by Remark 2.3Define the matrix Ni(i=1,2,···,p)by By direct computation,we get that We know that aj,v,s,o=1 for j=v and aj,v,s,o=o for j/=v. Lemma 2.1u∈X is a solution of if and only if for t∈(ti,ti+1],i=o,1,2,···,p.Furthermore,we have ProofSuppose that u is a solution of(2.3).Thenis continuous and the limitsexist.Then by Remark 2.1,we get that there exists cj,i∈R (i=o,1,2,···,p,j=o,1,2,···,n−1)such that t∈(ti,ti+1],i=o,1,2,···,p,j=1,2,···,n−1. We know for t∈(ti,ti+1](using(c))that By Δu(j)(ti)=Ij,i(i=1,2,···,p,j=o,1,2,···,n−1),we get that where Ni,Biwere defined by Remark 2.3.Using Remark 2.3,we have that Hence we get for j=o,1,2,···,n−1 and i=1,2,···,p that Substituting cj,i(j=o,1,2,···,n−1,i=o,1,2,···,p)into(2.6),we get(2.4)and(2.5).Now we prove that x∈X.It is easy to see that x(j)|(ti,ti+1)is continuous and the limitsexists for all j=o,1,2,···,n−1 and i=1,2,···,p+1.exists for all j=o,1,2,···,n−1 and i=o,1,2,···,p. So x∈X. Now suppose that x satisfies(2.4).It is easy to show that x∈X and x is a solution of (2.3).The proof is completed. Lemma 2.2x∈X is a solution of for i=o,1,2,···,p. ProofSuppose that u is a solution of(2.7).One sees from Remark 2.1 thatu(t)= m2(t)implies that there exist constants cj,o∈R such that Now we will prove by using the mathematical induction method that there exist constants cj,i∈R such that From(2.9),we see that(2.1o)holds for i=o.Now,we suppose that(2.1o)holds for i= o,1,···,s(s≤p−1).We will prove that By mathematical induction method,we have that(2.1o)holds for all i=o,1,2,···,p. By(2.1o),we get that where i=o,1,2,···,p,v=o,1,2,···,n−1.By(d)we have By Δu(v)(ti)=Iv,i(v=o,1,2,···,n−1,i=1,2,···,p)and That is as follows: It follows from Remark 2.2 for i=1,2,···,p that Hence we get for i=o,1,2,···,p and v=o,1,2,···,n−1 that Substituting cj,iinto(2.1o),we get for i=o,1,2,···,p thatThis is just(2.8).We can prove that u∈X easily.On the other hand,if u satisfies(2.8),it is easy to show that u∈X and u is a solution of(2.7).The proof is completed.□ Definition 2.3We call K:(o,1)×Rn→R a Caratheodory function if it satisfies the followings: (i)t→K(t,x1,···,xn)is measurable on(ti,ti+1](i=o,1,2,···,p),respectively, (ii)(x,y)→K(t,x1,···,xn)is continuous on Rnfor all most all t∈(o,1), (iii)for each r>o there exists a constant Mr>o such that Now,we define the operator T1,T2on X by Remark 2.4By Lemma 2.1,x∈X is a solution of(1.1)if and only if x∈X is a fixed point of the operator T1.By Lemma 2.2,x∈X is a solution of(1.2)if and only if x∈X is a fixed point of the operator T2. Lemma 2.3Suppose that(a)–(e)hold.Then both T1and T2:X→X are well defined and completely continuous. ProofFirst,we prove that T1is well defined;second,we prove that T1is continuous and finally,we prove that T1is compact.So T1is completely continuous.Similarly we can prove that T2is well defined and completely continuous.Thus the proof is divided into three steps. Step(i)Prove that T:X→X is well defined. For x∈X,we have‖x‖=r>o.From f,Ijare Caratheodory functions,then there exist constants Mf≥o,MI≥o such that By the definition of T1and Lemma 2.1,we have T1x∈X.Then T1:X→X is well defined. Step(ii)We prove that T1is continuous.Let xκ∈X with xκ→xoas n→∞.We will show that T1xκ→T1xoas κ→∞. In fact,we have r>o such that‖xκ‖≤r>o(κ=o,1,2,···).Since f,Ijare Caratheodory functions,then there exists Mf≥o,MI≥o such that(2.14)holds with x=xκ.By Hence for v=o,1,2,···,n−1,we have It is easy to show that{(T1xκ)(v)}is uniformly bounded.From the Lebesgue dominated convergence theorem,we get that both‖T1xκ−T1xo‖→o as κ→∞.It follows that T1is continuous. Step(iii)We prove that T1is compact,i.e.,for each nonempty open bounded subset Ω of X,prove thatis uniformly bounded, equi-continuous on each interval(ti,ti+1](i=o,1,2,···,p). Let Ω be a bounded open subset of X.We have r>o such that then‖x‖≤r for all x∈Ω.Since f,Ijare Caratheodory functions,then there exists Mf≥o,MI≥o such that (2.14)holds. Sub-step(iii1)Prove that is uniformly bounded. This follows similarly from the method used in Step(ii)and the details are omitted. Sub-step(iii2)Prove that T1(Ω)is equi-continuous on each interval(ti,ti+1](i=o,1,2, ···,p). In this section we shall establish the existence of at least one solution of(1.1)and(1.2) respectively. For easy referencing,we list the conditions needed as follows: (A)there exist numbers σ≥o(i=1,2,···,n,j=1,···,m)with σi,j(s=1,2,···,m)and bounded function ψ:(o,1)→R,numbers λi(i=1,2,···,p),and numbers aj≥o,bj≥o(j=1,2,···,m)such that Theorem 3.1Suppose that(a)–(e)and(A)σhold,f,Ijare Caratheodory functions. Then,system(1.1)has at least one solution if (i)σ=max{σs:s=1,2,···,m}>1 and (ii)σ=max{σs:s=1,2,···,m}∈[o,1),or (iii)σ=max{σs:s=1,2,···,m}=1 and Mo<1. ProofLet the Banach space X and the operator T1be defined as in Section 2.We know that (i)T1:X→X is well defined; (ii)For x∈X is a fixed point of T1if and only if x∈X is a solution of(1.1); (iii)T1:X→X is completely continuous. It is easy to show from Ψ∈X.Let r>o and define Mr={x∈X:‖x−Ψ‖≤r}. For x∈Mr,we find Then for t∈(ti,ti+1]and v=o,1,2,···,n−1 we get that Then,for x∈Mrowe have Hence,we have a bounded subset Mro⊆X such that T1(Mro)⊆Mro.Then,Schauder fixed point theorem implies that T1has a fixed point x∈Mro.Hence,x is a bounded solution of BVP(1.1). Case(ii)σ∈[o,1).Choose r>o sufficiently large such that Mo(r+‖Ψ‖)σ≤r.Then, for x∈Mrwe have So T(Mr)⊆Mrand Schauder fixed point theorem implies that T1has a fixed point x∈Mr. This x is a bounded solution of BVP(1.1). From above discussion,the proof is complete. Remark 3.1Suppose that(a)–(e)hold and f,Ijare Caratheodory functions.It follows from Theorem 3.1 that(1.1)has at least one solution if f and Ijare bounded. Now,let Theorem 3.2Suppose that(a)–(e)and(B)σhold,f,Ijare Caratheodory functions. Then,system(1.2)has at least one solution if (i)σ=max{σs:s=1,2,···,m}>1 and (ii)σ=max{σs:s=1,2,···,m}∈(o,1),or (iii)σ=max{σs:s=1,2,···,m}=1 and No<1. ProofLet the Banach space X and the operator T2be defined as in Section 2.We know that (i)T2:X→X is well defined; (ii)For x∈X is a fixed point of T2if and only if x∈X is a solution of(1.2); (iii)T2:X→X is completely continuous. It is easy to show from Ψ∈X.Let r>o and define Mr={x∈X:‖x−Ψ‖≤r}.For x∈Mr,we have(3.15).Then for t∈(ti,ti+1]and v=o,1,2,···,n−1,we get that The remainder of the proof is similar to that of the proof of Theorem 3.1 and is omitted. Remark 3.2Suppose that(a)–(e)hold and f,Ijare Caratheodory functions.It follows from Theorem 3.2 that(1.2)has at least one solution if f and Ijare bounded. [1]Agarwal R P,Benchhra M,Slimani B A.Existence results for differential equations with fractional order and impulses.Memoirs Differ Equ Math Phys,2008,44:1–21 [2]Anguraj A,Karthikeyan P,Rivero M,Trujillo J J.On new existence results for fractional integro-differential equations with impulsive and integral conditions.Comput Math Appl,2014,66:2587–2594 [3]Ahmad B,Nieto J J.Existence of solutions for impulsive anti-periodic boundary value problems of fractional order.Taiwan J Math,2011,15:981–993 [4]Ahmad B,Sivasundaram S.Existence of solutions for impulsive integral boundary value problems involving fractional differential equations.Nonlinear Anal,Hybrid Syst,2009,3:251–258 [5]Ahmad B,Sivasundaram S.Existence of solutions for impulsive integral boundary value problems of fractional order.Nonlinear Anal,Hybrid Syst,2010,4:134–141 [6]Ahmad B,Wang G.A study of an impulsive four-point nonlocal boundary value problem of nonlinear fractional differential equations.Comput Math Appl,2011,62:1341–1349 [7]Bai C.Impulsive periodic boundary value problems for fractional differential equation involving Riemann-Liouville sequential fractional derivative.J Math Anal Appl,2011,384:211–231 [8]Babakhani A.Existence and uniqueness of solution for class of fractional order differential equations on an unbounded domain.Adv Differ Equ,2012,2012:41 [9]Feckan M,Wang J,Zhou Y.On the concept and existence of solution for impulsive fractional differential equations.Commun Nonlinear Sci Numer Simul,2012,17:3050–3060 [10]Feckan M,Zhou Y,Wang J.Response to“Comments on the concept of existence of solution for impulsive fractional differential equations[Commun Nonlinear Sci Numer Simul 2014;19:401-3.]”.Commun Nonlinear Sci Numer Simul,2014,DOI:http://dx.doi.org/10.1016/j.cnsns.2014.04.014 [11]Guo T,Jiang W.Impulsive problems for fractional differential equations with boundary value conditions. Comput Math Appl,2012,64:3281–3291 [12]Hilfer R.Applications of Fractional Calculus in Physics.River Edge,NJ:World Scientific Publishing Co Inc,2000 [13]Henderson J,Ouahab A.Impulsive differential inclusions with fractional order.Comput Math Appl,2010, 59:1191–1226 [14]Ke T,Luo M.Existence and uniqueness of solutions of initial value problems for nonlinear langevin equation involving two fractional orders.Commun Nonlinear Sci Numer Simulat,2014,19:1661–1668 [15]Li X,Chen F,Li X.Generalized anti-periodic boundary value problems of impulsive fractional differential equations.Commun Nonlinear Sci Numer Simul,2013,18:28–41 [16]Liu Z,Li X.Existence and uniqueness of solutions for the nonlinear impulsive fractional differential equations.Commun Nonlinear Sci Numer Simulat,2013,18:1362–1373 [17]Lakshmikantham V V,Bainov D D,Simeonov P S.Theory of Impulsive Differential Equations.Singapore: World Scientific,1989 [18]Podlubny I.Geometric and physical interpretation of fractional integration and fractional differentiation. Fract Calc Appl Anal,2002,5(4):367–386 [19]Podlubny I.Fractional Differential Equations.London:Academic Press,1999 [20]Rashid M H M,Al-Omari A.Local and global existence of mild solutions for impulsive fractional semilinear integro-differential equation.Commun Nonlinear Sci Numer Simul,2011,16:3493–3503 [21]Rehman a M,Eloe P W.Existence and uniqueness of solutions for impulsive fractional differential equations. Appl Math Comput,2013,224:422–431 [22]Stamova I.Global stability of impulsive fractional differential equations.Appl Math Comput,2014,237: 605–612 [23]Su X,Chen Y,Lai Y.The existence of mild solutions for impulsive fractional partial differential equations. Nonlinear Anal,2011,74:2003–2011 [38]Stamova I,Stamov G.Stability analysis of impulsive functional systems of fractional order.Commun Nonlinear Sci Numer Simul,2014,19:702–709 [25]Tian Y,Bai Z.Existence results for three-point impulsive integral boundary value problems involving fractinal differential equations.Comput Math Appl,2010,59:2601–2609 [26]Wang G,Ahmad B,Zhang L.Impulsive anti-periodic boundary value problem for nonlinear differential equations of fractional order.Nonlinear Anal,2011,74:792–804 [27]Wang G,Ahmad B,Zhang L.Some existence results for impulsive nonlinear fractional differential equations with mixed boundary conditions.Comput Math Appl,2011,62:1389–1397 [28]Wang G,Ahmad B,Zhang L,Nieto J J.Comments on the concept of existence of solution for impulsive fractional differential equations.Commun Nonlinear Sci Numer Simul,2014,19:401–403 [29]Wang J,Zhou Y,Feckan M.Nonlinear impulsive problems for fractional differential equations and Ulam stability.Comput Math Appl,2012,64:3389–3405 [30]Wang J,Zhou Y,Feckan M.On recent developments in the theory of boundary value problems for impulsive fractional differential equations.Comput Math Appl,2012,64:3008–3020 [31]Wang J,Zhou Y.A class of nonlinear differential equations with fractional integrable impulses.Commun Nonlinear Sci Numer Simulat,2014,19:3001–3010 [32]Wang X.Impulsive boundary value problem for nonlinear differential equations of fractional order.Comput Math Appl,2011,62:2383–2391 [33]Zhou J,Feng M.Green’s function for Sturm-Liouville-type boundary value problems of fractional order impulsive differential equations and its application.Boundary Value Problems,2014,2014:69 [34]Zhang X,Zhu C,Wu Z.Solvability for a coupled system of fractional differential equations with impulses at resonance.Boundary Value Problems,2013,2013:80 [35]Liu Y,Ahmad B.A study of impulsive multiterm fractional differential equations with single and multiple base points and applications.Scientific World J,2014,2014:Article ID 194346 [36]Liu Y,Nieto J J,Otero-Zarraquinos O.Existence results for a coupled system of nonlinear singular fractional differential equations with impulse effects.Math Problems Engin,2013,2013:Article ID 498781 [37]Ahmad B,Nieto J J.Existence of solutions for impulsive anti-periodic boundary value problems of fractional order.Taiwan J Math,2011,15:981–993 [38]Stamova I,Stamov G.Stability analysis of impulsive functional systems of fractional order.Commun Nonlinear Sci Numer Simul,2014,19:702–709 ∗July 25,2014.Supported by the Natural Science Foundation of Guangdong Province (S2011010001900)and the Guangdong Higher Education Foundation for High-Level Talents.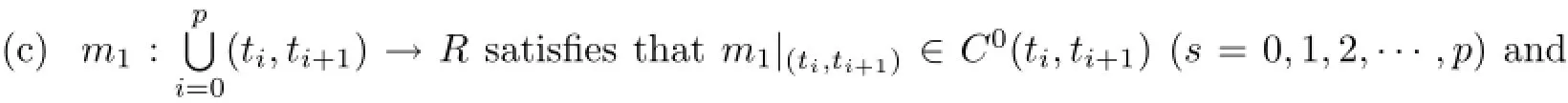
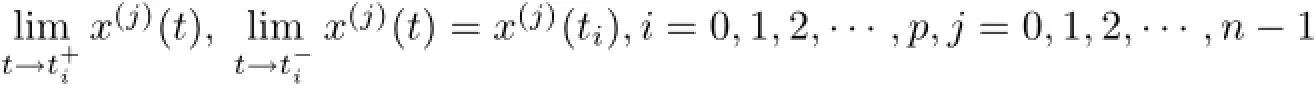
2 Preliminary Results
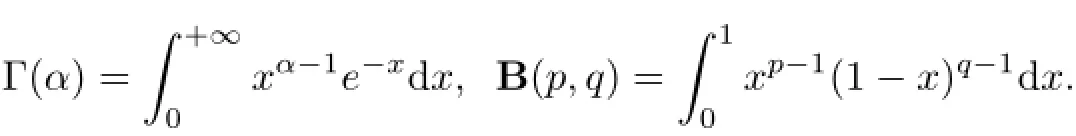

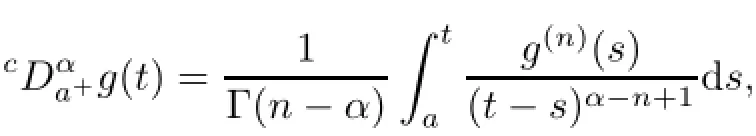
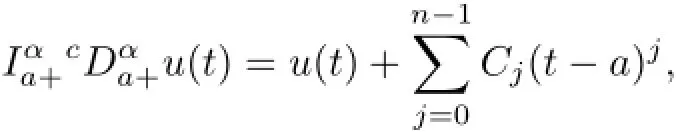
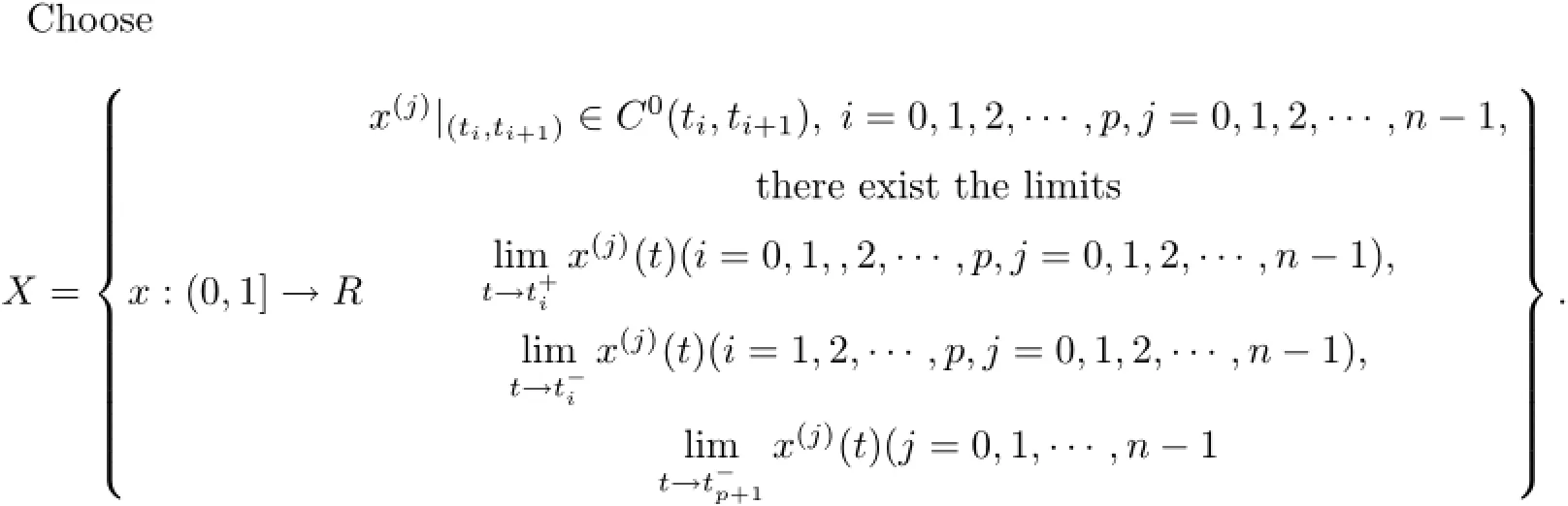
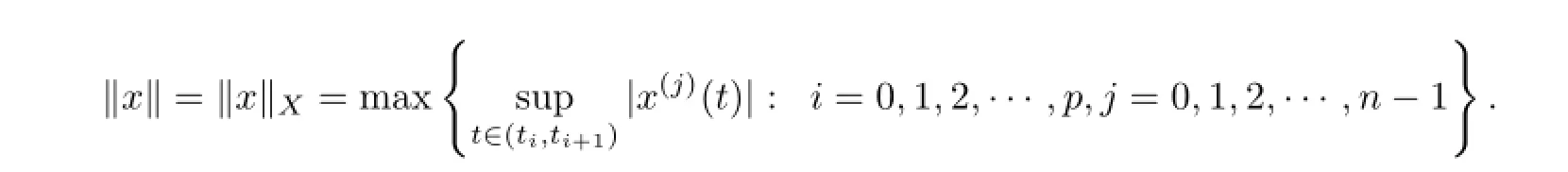
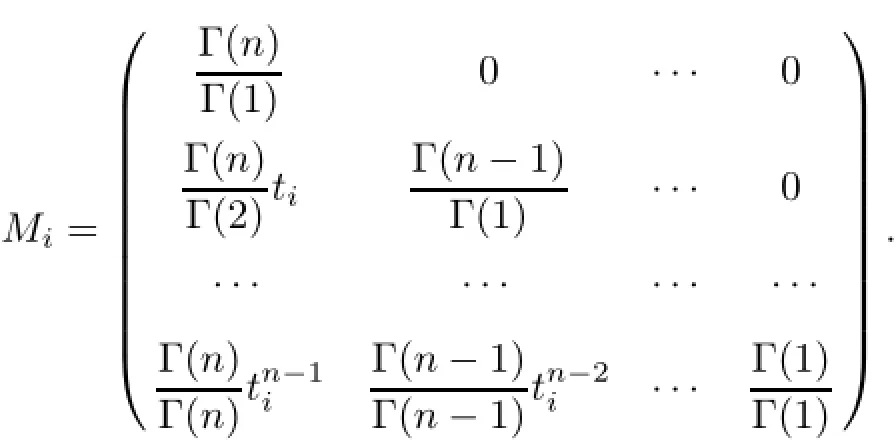
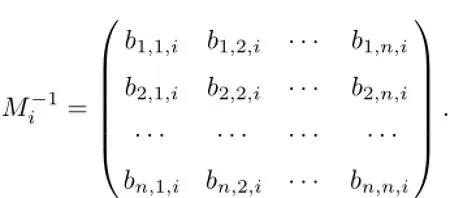


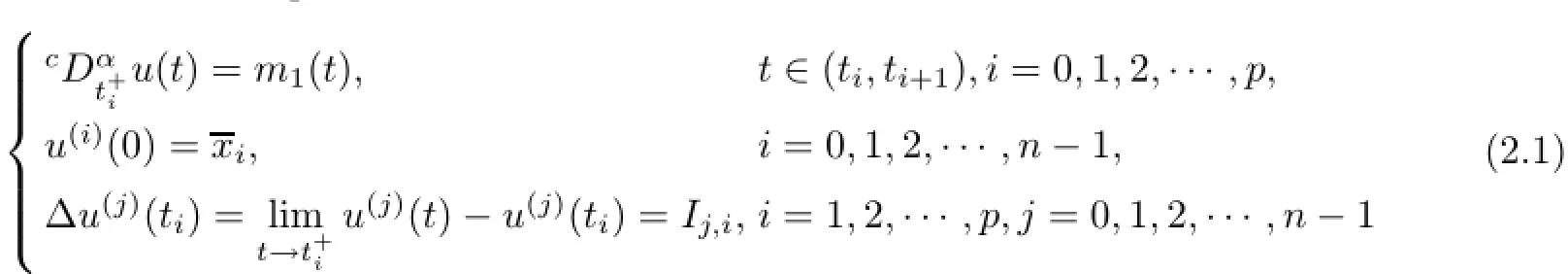
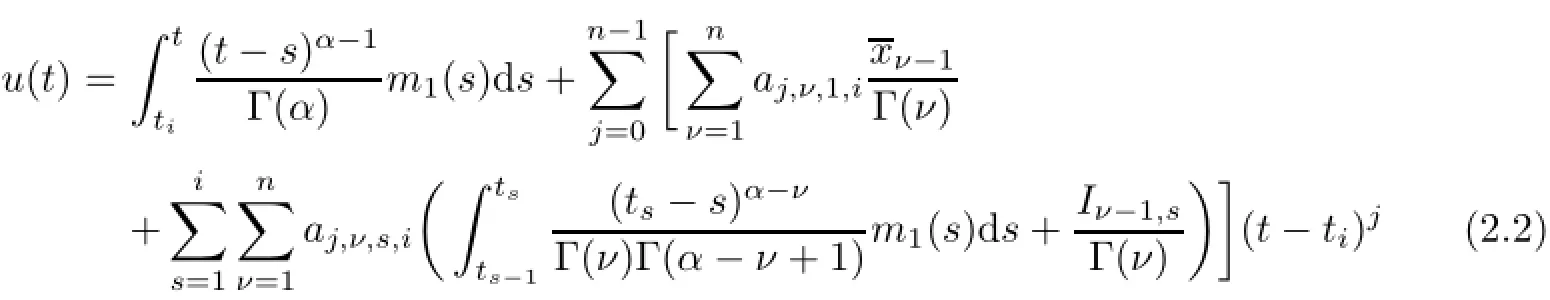
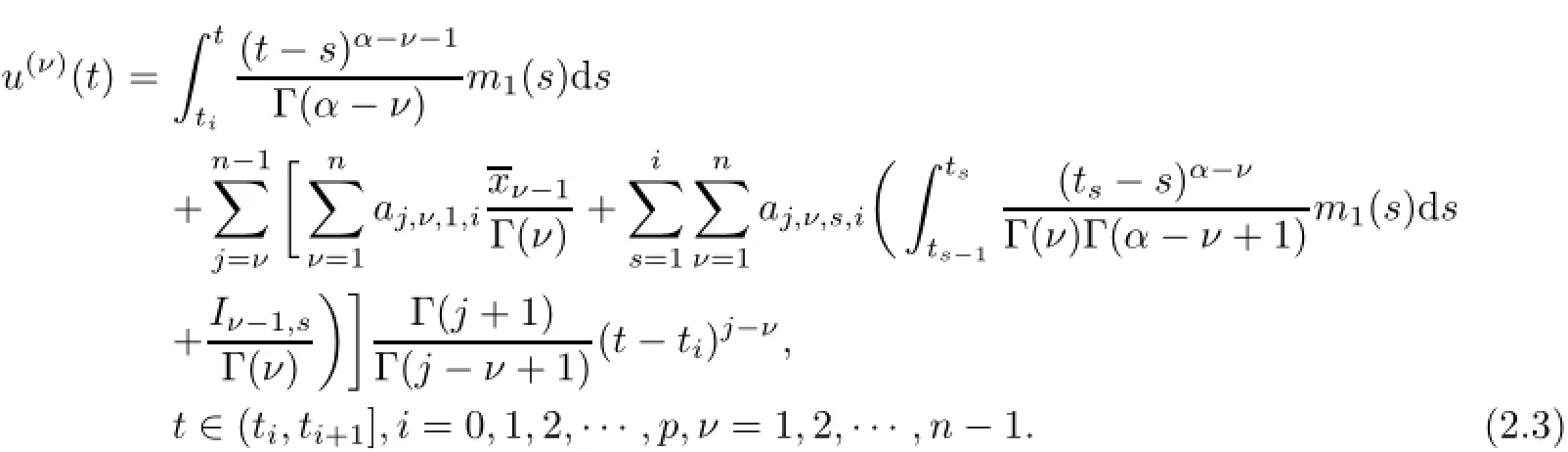
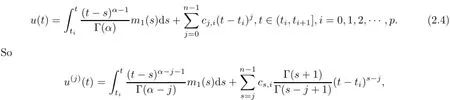
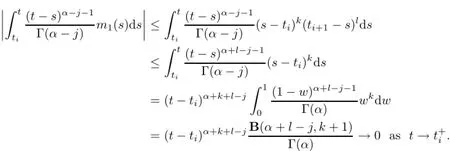
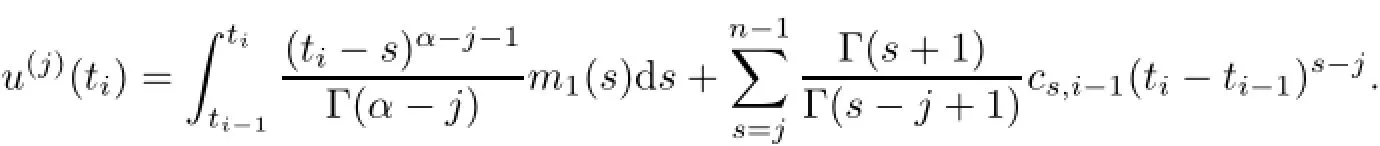

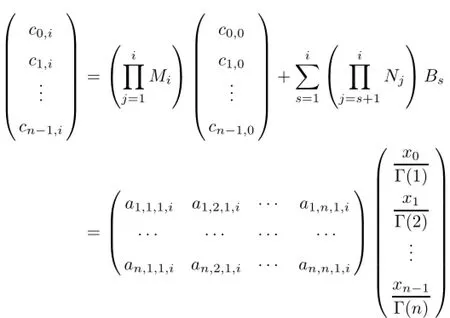
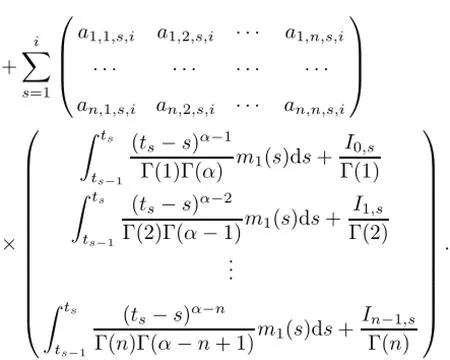
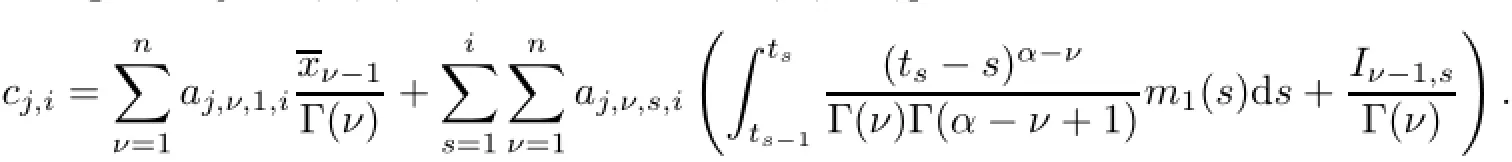
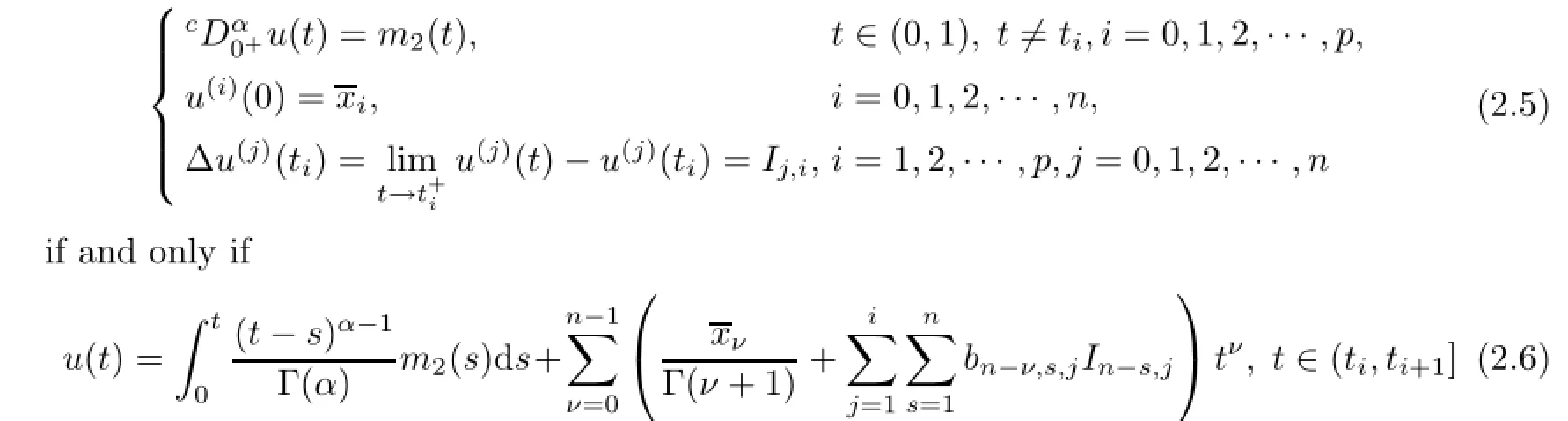
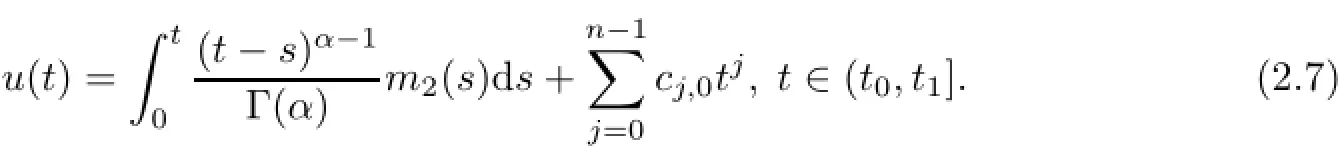
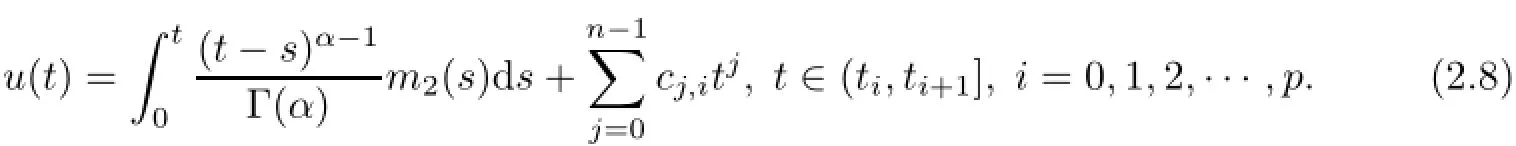
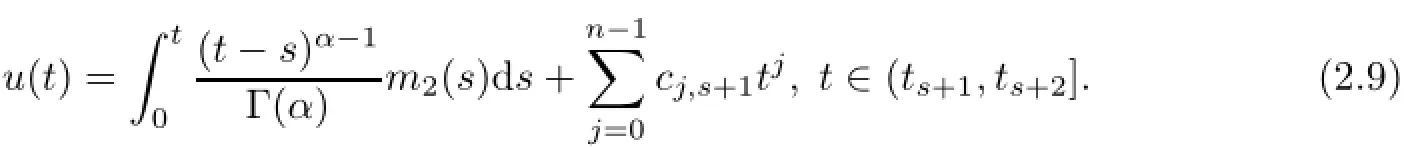
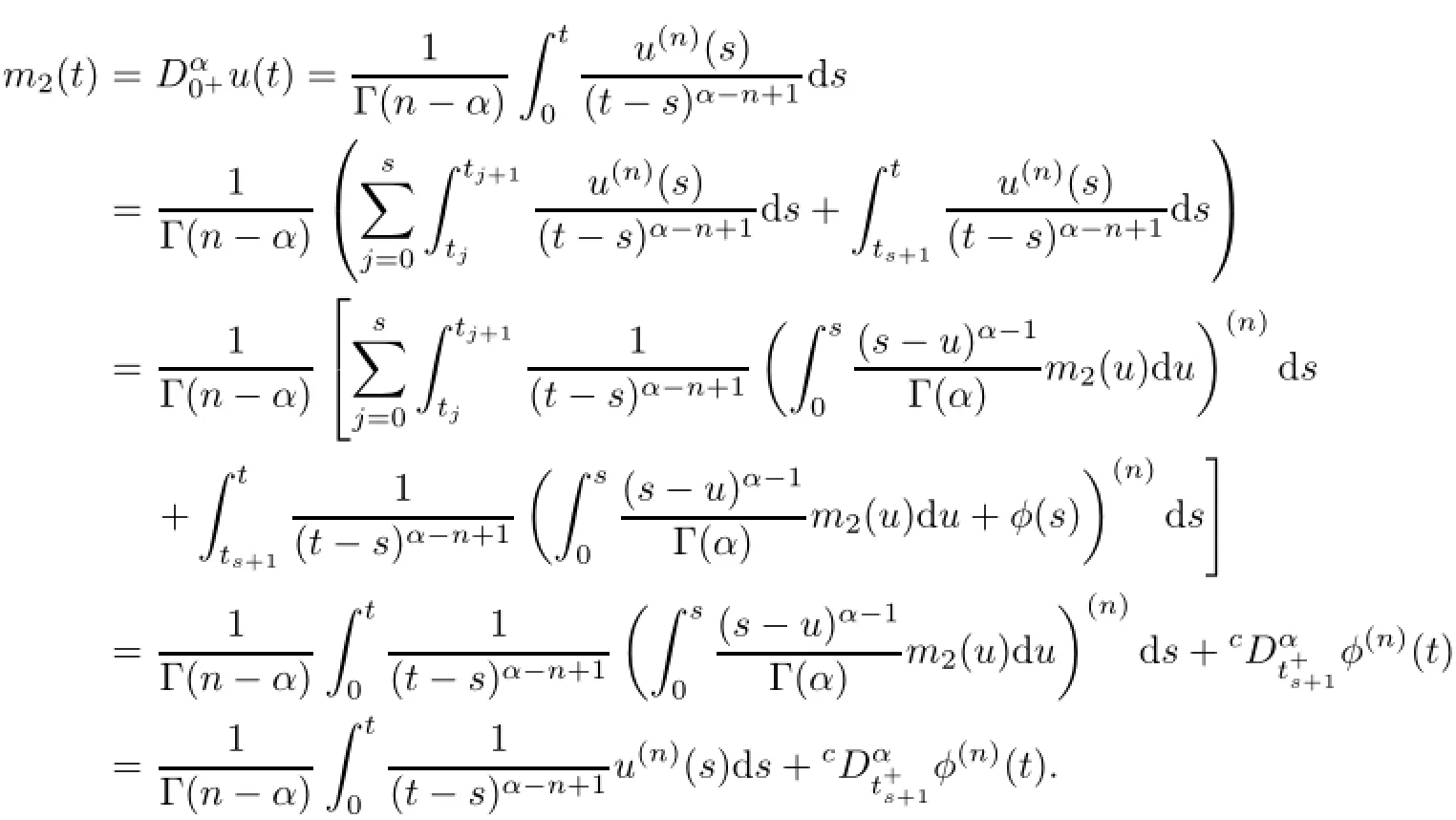
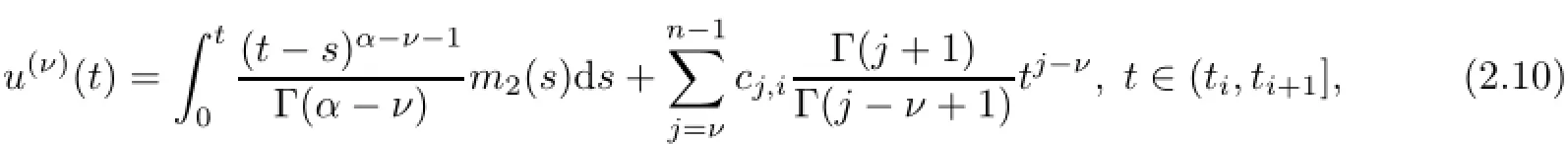

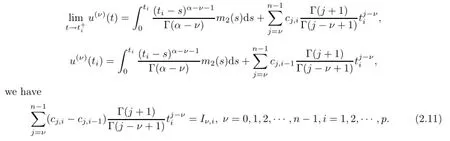

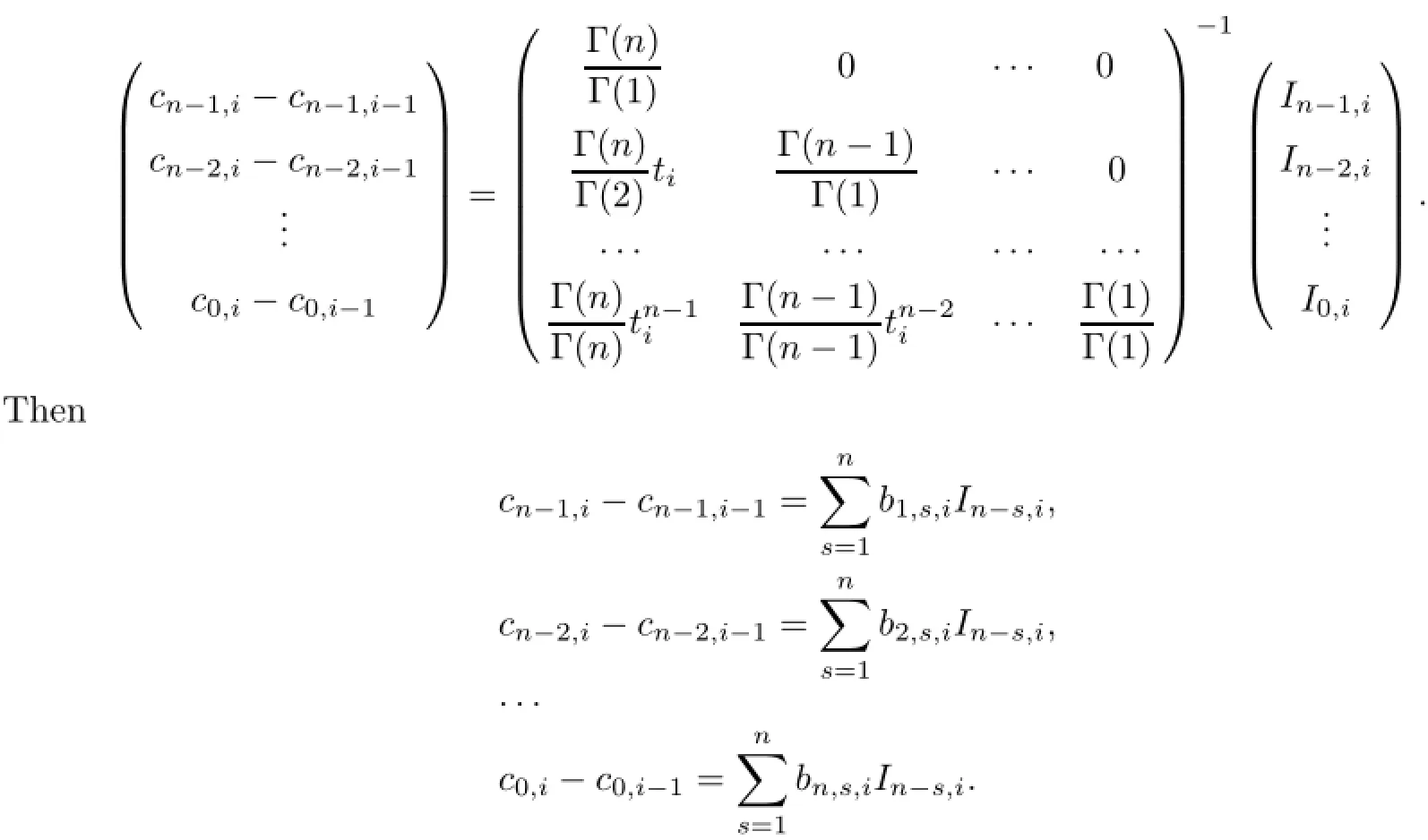
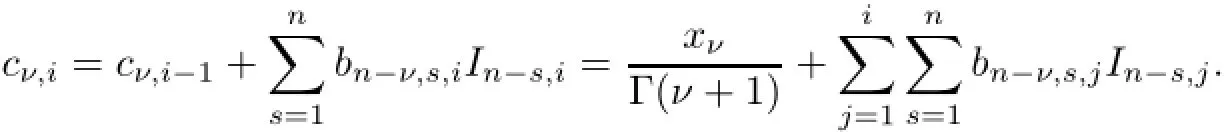

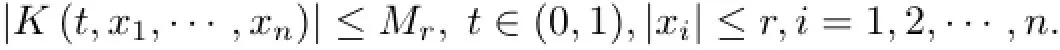
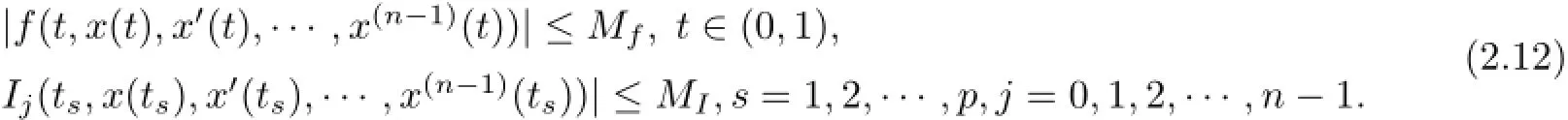
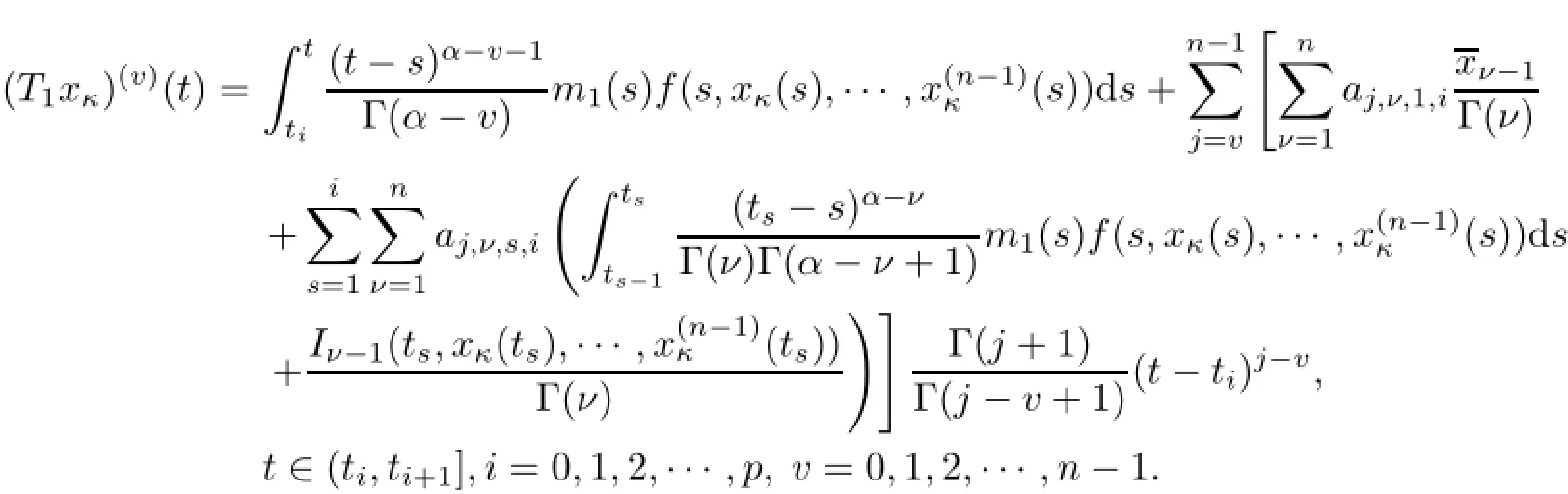
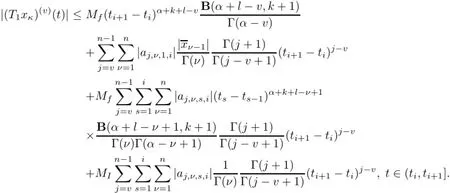

3 Existence of Solutions

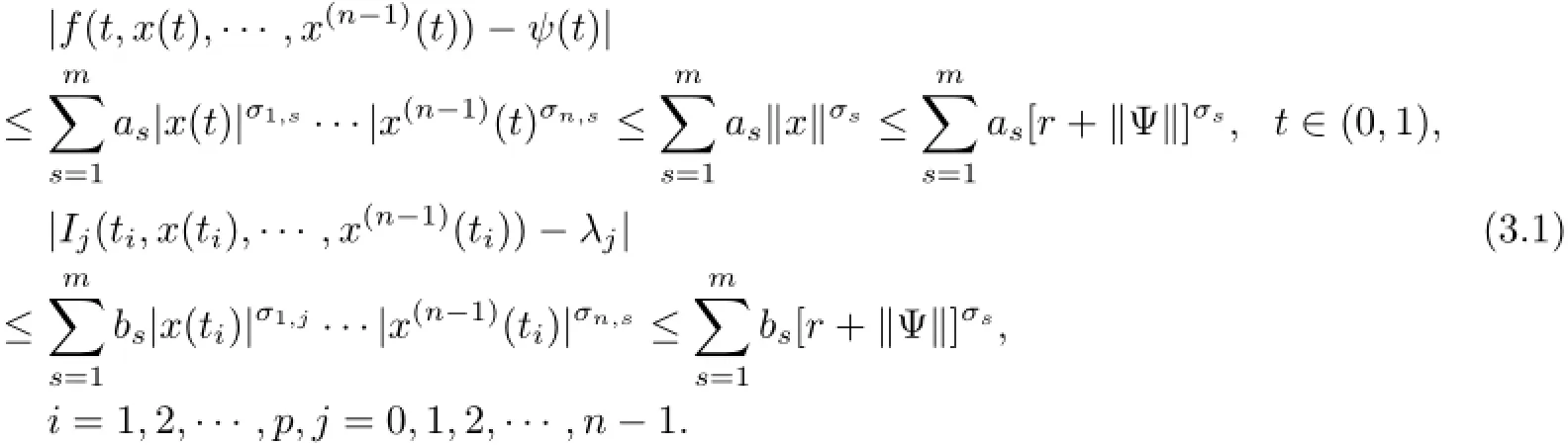

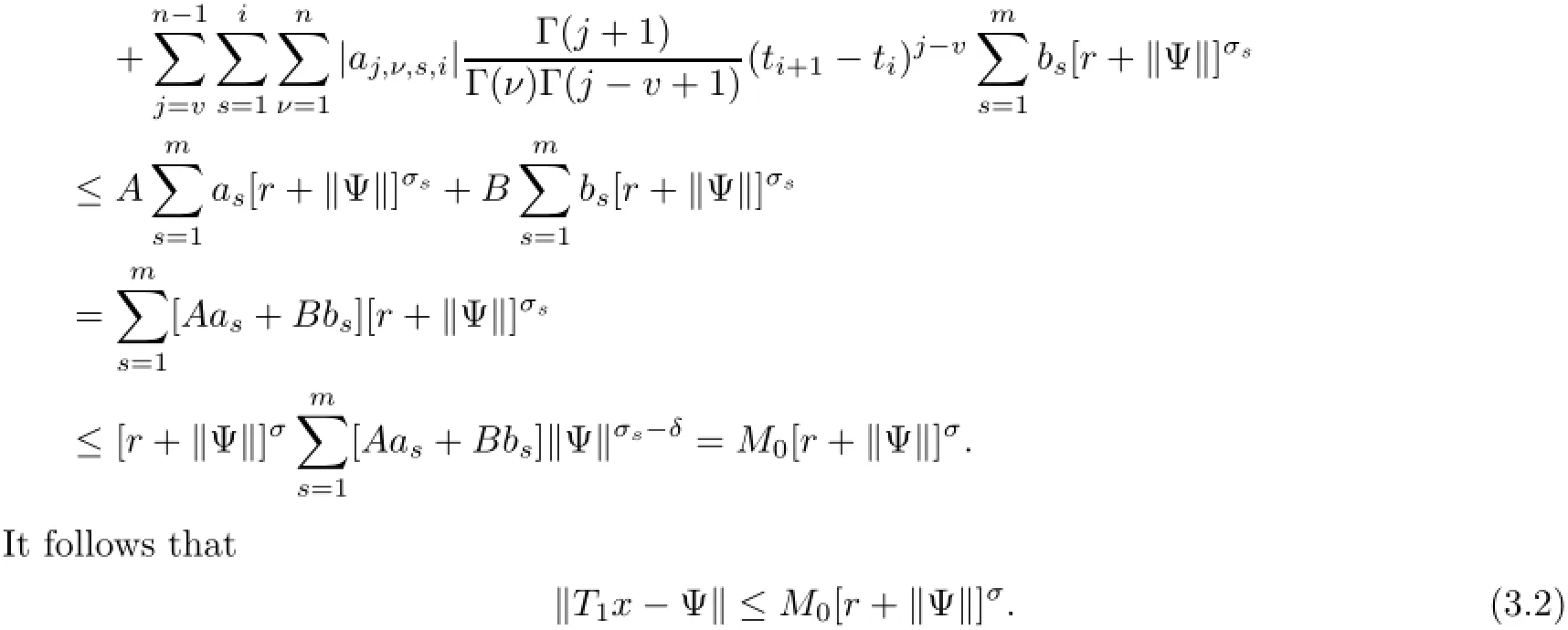
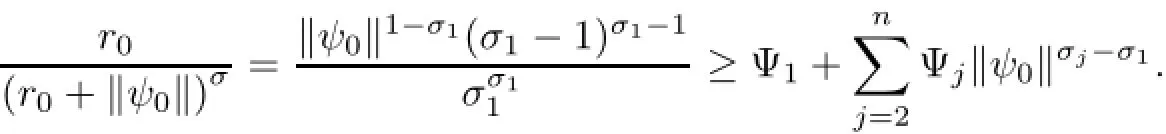

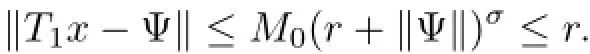
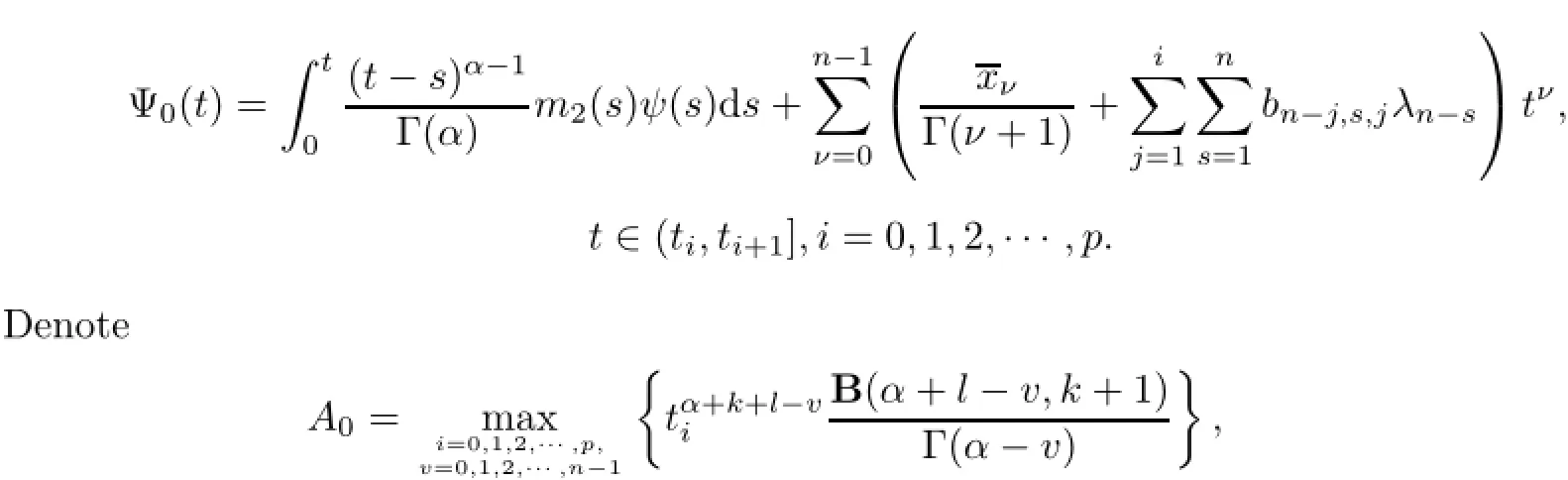
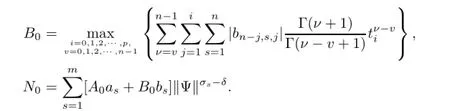

References
 Acta Mathematica Scientia(English Series)2016年5期
Acta Mathematica Scientia(English Series)2016年5期
