COEXISTENCE FOR MULTIPLE LARGEST REPRODUCTION RATIOS OF A MULTI-STRAIN SIS EPIDEMIC MODEL∗

Yoshiaki MUROYADepartment of Mathematics,Waseda University,3-4-1 Ohkubo,Shinjuku-ku,Tokyo 169-8555,Japan E-mail:ymuroya@waseda.jp

Eleonora MESSINAElvira RUSSO Dipartimento di Matematica e Applicazioni,Universit`a degli Studi di Napoli“Federico II”-Via Cintia, I-80126 Napoli,Italy E-mail:eleonora.messina@unina.it;elvrusso@unina.it

Antonia VECCHIO Istituto per Applicazioni del Calcolo“M.Picone”,Sede di Napoli-CNR-Via P.Castellino, 111-80131 Napoli,Italy E-mail:a.vecchio@iac.cnr.it

COEXISTENCE FOR MULTIPLE LARGEST REPRODUCTION RATIOS OF A MULTI-STRAIN SIS EPIDEMIC MODEL∗

Yoshiaki MUROYA†Department of Mathematics,Waseda University,3-4-1 Ohkubo,Shinjuku-ku,Tokyo 169-8555,Japan E-mail:ymuroya@waseda.jp

Eleonora MESSINAElvira RUSSO Dipartimento di Matematica e Applicazioni,Universit`a degli Studi di Napoli“Federico II”-Via Cintia, I-80126 Napoli,Italy E-mail:eleonora.messina@unina.it;elvrusso@unina.it

Antonia VECCHIO Istituto per Applicazioni del Calcolo“M.Picone”,Sede di Napoli-CNR-Via P.Castellino, 111-80131 Napoli,Italy E-mail:a.vecchio@iac.cnr.it

In this paper,to complete the global dynamics of a multi-strains SIS epidemic model,we establish a precise result on coexistence for the cases of the partial and complete duplicated multiple largest reproduction ratios for this model.

multi-strains SIS epidemic model;global attractivity;Lyapunov function;co

existence

2010 MR Subject Classification34K20;34K25;92D30

1　Introduction

In this paper,we were interested in the works of Bichara et al.[2]and Martcheva[9]on SIS models with standard mass action and varying population,with n different pathogen strains of an infectious disease(for a review report on infectious diseases,see for example,[6]).

To understand the factors that lead to coexistence or to competitive exclusion have much attentions(see for example,[3],[4]and[13])and in the absence of multiple infections and the presence of complete cross-immunity,only the parasite strain for the maximal basic reproduction ratio,persists.However the validity of such a principle was challenged and only quite a few restrictions of this result were proved.For example,when the infection is transmitted bothvertically and horizontally,simulations of[8]showed that strains with lower virulence can outcompete strains with higher basic reproduction ratio.

For a non-autonomous multi-strain SIS epidemic model with periodic coefficients,Martcheva [9]established local and global stability of the disease-free equilibrium and existence and uniqueness of a single-strain periodic solution using the conditions of the invasion reproduction ratio and the strain with the largest reproductive ratio eliminates the rest.

For a spatially distributed periodic multi strain SIS epidemic model with periodic migration rates,Marv´a et al.[1o]considered a migration of the susceptible and infected individuals between patches such that migrations are much faster than the epidemic process,and defining global reproduction numbers in the non-spatialized aggregated system,they showed that adequate periodic fast migrations can in many cases reverse local endemicity and get global eradication of the epidemic.

Recently,applying Lyapunov functional approach but a completely different usage from the well known one(see for example,[1],[7]and[11]),Bichara et al.[2]proved that for an isolated largest reproduction ratio,this strain persists while the others die out,and for completely duplicated largest reproduction ratios,the complete coexistence with minimum total population of all the strains occur to the following multi-strain SIS epidemic model with n different pathogen strains of an infectious disease.

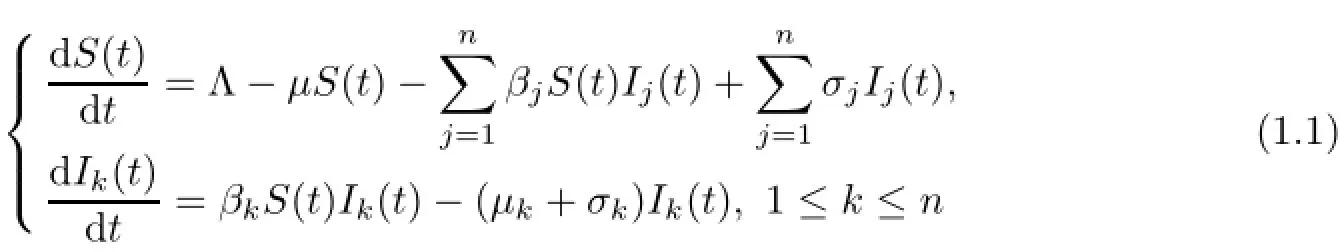
with the initial conditions

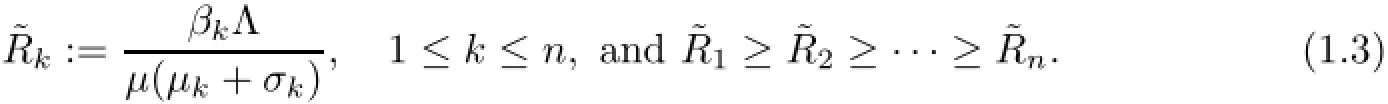
By(1.2),similar to Muroya et al.[12,Lemma 2.1]or Kuniya and Muroya[7,Lemma 2.1], we have S(t)>o,Ik(t)>o,k=1,2,···,n for any t>o.For system(1.1),the feasible region Γn+1is defined by

By Bichara et al.[2,Section 2.2],we haveand we always have a uniquedisease-free equilibrium Eo=(So,o,o,···,o)in Γn+1and when the basic ratio is greater than one,then some boundary endemic equilibria appear in Γn+1.Note that

Theorem A(see Bichara et al.[2,Theorems 1–3])

(i)If˜Ri≤1,i=1,2,···,n,then the disease-free equilibrium

Eo=(So,o,o,···,o),So=is globally asymptotically stable in Γn+1.

(ii)If

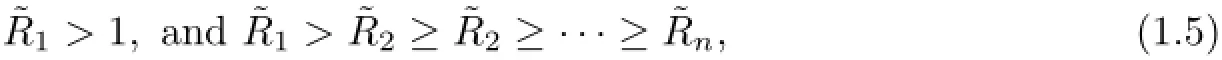
then there exists a saturated equilibrium

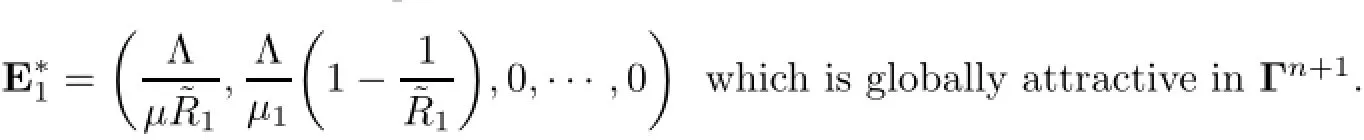
(iii)’If

then the equilibrium set S is globally asymptotically stable,where S is defined by

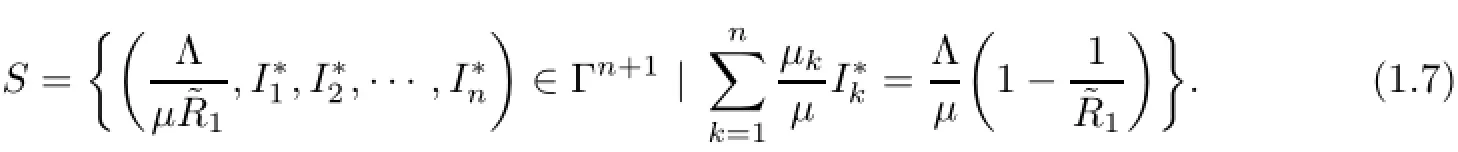
This is a very interesting result of(1.1),but we have some questions on this last result (iii)’,for example,how to determine the existence of thek=1,2,···,n and the concrete values ofof the equilibrium in S.Moreover,how about the case that if there exists a positive integer ko∈{2,···,n−1}such that

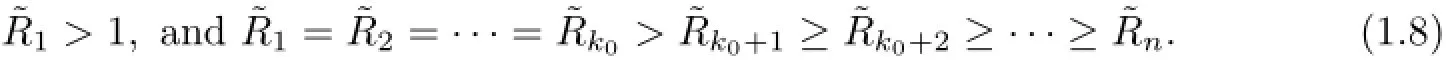
Therefore,we think to complete the global dynamics of this multi-strains SIS epidemic model(1.1),there is a remaining problem to investigate a precise result on the above questions in the partial or complete coexistence for the cases of multiple largest reproduction ratios for a multi-strains SIS epidemic model(1.1).

Motivated by the above result,in this paper,applying the result of Martcheva[9],we establish the global dynamics of the partial or complete coexistence for the cases of multiple largest reproduction ratios for a multi-strains SIS epidemic model(1.1).The obtained result is the following.

Theorem 1.1If there exists a positive integer ko∈{2,···,n}such that

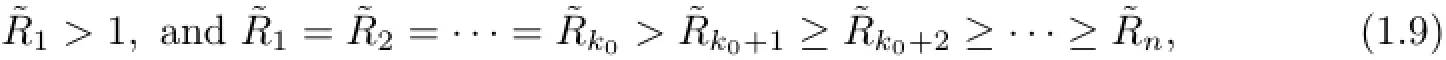
then S(t),Ik(t),1≤k≤koof system(1.1)is persistent and others are die out in Γn+1,and

where x=ˆx is a unique positive solution of the following equation:

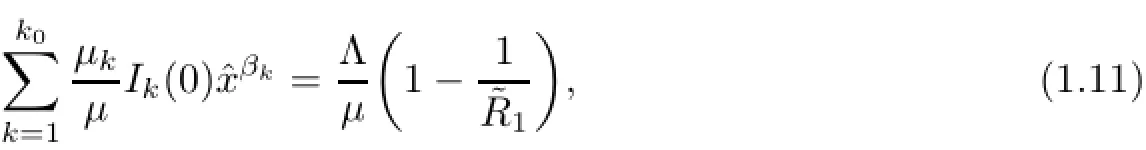
Together with Bichara et al.[2,Theorems 1 and 2](see(i)and(ii)of Theorem A),we established complete global dynamics of the multi-strains SIS epidemic model(1.1).

The organization of this paper is as follows.In Section 2,we offer some known results for system(1.1)obtained by Martcheva[9,Section 2].In Section 3,using the result of Martcheva [9,Section 2],we establish a precise result on the partial coexistence for the remaining cases of multiple largest reproduction ratios for(1.1)(see Theorem 3.2).Finally,in Section 4,we end this note by conclusions.

2　Preliminary

In this section,we only consider the case that(1.9)holds.Then,by(1.3),(1.9)is equivalent to

Dividing by ηk(t),integrating from zero to t,we are lead to

where by(1.2),ηk(o)>o,1≤k≤n.By(2.1),we have the important relation that ηk(t)= ηk(o),for any t>o 1≤k≤koand taking the limit as t→+∞,then ηk(t)→o,as t→+∞,ko+1≤k≤n.Thus,we obtain

3　Global Attractivity of a Saturated Equilibrium of a Rduced System

In this section,under the condition ko∈{2,3,···,n}for(1.9),consider a saturated equi-

Lemma 3.1If(1.9)holds,then(1.1o)and(1.11)hold.

ProofBy(2.1)and(2.2),we have

Moreover,by the first equation of(1.1),ifS(t)=S∗,then

from which we obtain

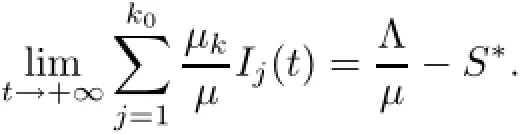
Then,by(2.2),we have

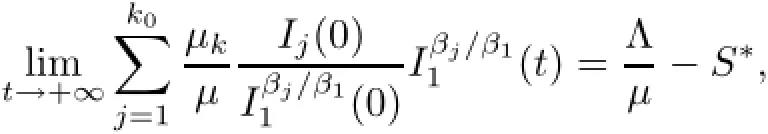
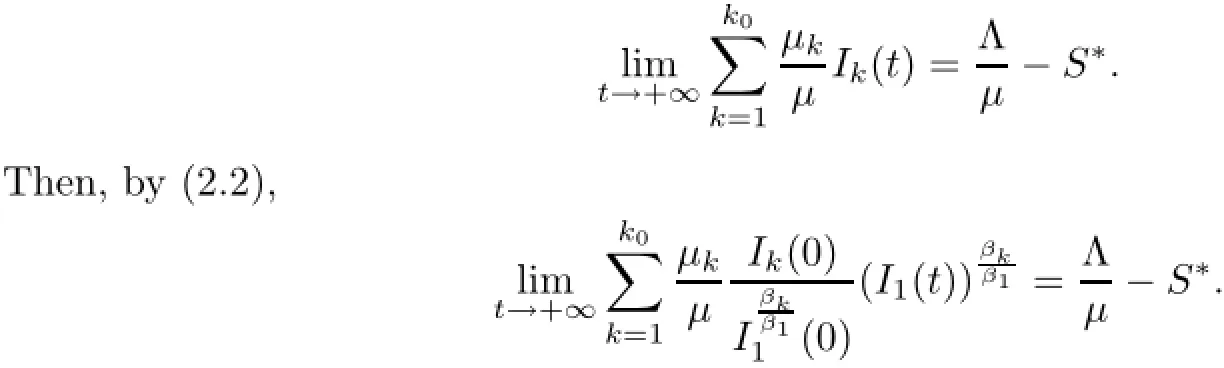
Notice that the left hand sizeis a strictly monotone increasing function of I1on[o,+∞)and there exists an upper boundThen,for the initial conditions(1.2),there exists unique>o which depends on(1.2)and satisfies the following equation:

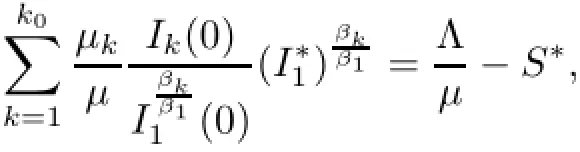
By the above discussion with additional koequations of the first part and inequalities of the second part of(2.1),we consider the global attractivity of a reduced n−ko+2 dimensional system of(1.1)for n−ko+2 arguments(S,˜Iko,Iko+1,Iko+2,···,In)in Γn−ko+2such that and we obtain the following theorem.

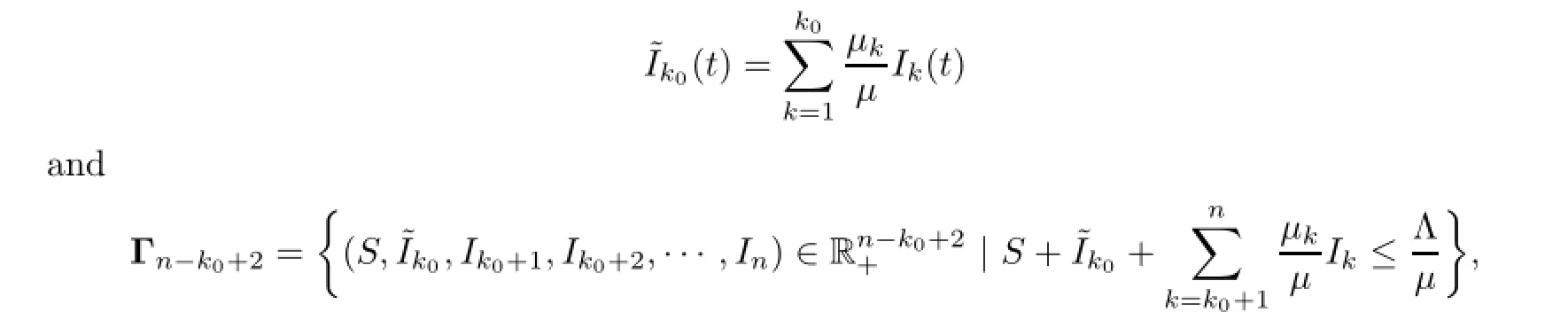
Theorem 3.2For ko∈{2,3,···,n}defined by(1.9),the endemic equilibrium˜Eko=

of the reduced n−ko+2 dimensional system of(1.1)for n−ko+2 arguments(S,˜Iko,Iko+1,Iko+2,···,In)is globally attractive in Γn−ko+2,and I∗k>o,1≤k≤kosatisfy(1.12)but depend on initial conditions I1(o),I2(o),···,Iko(o).

Proof of Theorem 1.1By Lemma 3.1 and Theorem 3.2,we can easily obtain Theorem 1.1.

4　Conclusions

In this paper,applying the result of Martcheva[9],we establish a precise result on coexistence for both cases of the partial and complete duplicated multiple largest reproduction ratios for a multi-strains SIS epidemic model(see Theorem 1.1).As a result,together with Bichara et al.[2,Theorems 1 and 2],we obtain the complete global dynamics of this model.

References

[1]Enatsu Y,Nakata Y,Muroya Y.Global stability of SIRS epidemic models with a class of nonlinear incidence rates and distributed delays.Acta Mathematica Scientia,2012,32B:851–865

[2]Bichara D,Iggidr A,Sallet G.Global analysis of multi-strains SIS,SIR and MSIR epidemic models.J Appl Math Comput,2014,44:273–292

[3]Dhirasakdanon T,Thieme H R.Persistence of vertically transmitted parasite strains which protect against more virulent horizontally transmitted strains//Modeling and Dynamics of Infectious Diseases.Ser Contemp Appl Math,11.Beijing:Higher Education Press,2009:187–215

[4]Dhirasakdanon T,Thieme H R.Stability of the endemic coexistence equilibrium for one host and two parasites.Math Model Nat Phenom,2010,5:109–138

[5]Faria T,Muroya Y.Global attractivity and extinction for Lotka-Volterra systems with infinite delay and feedback controls.Proc Royal Soc Edinb:Sec A,2015,145:301–330

[6]Hethcote H W.The Mathematics of infectious diseases.SIAM Review,2000,42:599–653

[7]Kuniya T,Muroya Y.Global stability of a multi-group SIS epidemic model for population migration. Discrete and Continuous Dynamical Systems-Series B,2014,19:1105–1118

[8]Lipsitch M,Nowak M A,Ebert D,May R M.The population dynamics of vertically and horizontally ransmitted parasites.Proc Biol Sci,1995,260:321–327

[9]Martcheva M.A non-autonomous multi-strain SIS epidemic model.J Biol Dyn,2009,3:235–251

[10]Marv´a M,Bravo de la Parra R,Poggiale J-C.Approximate aggregation of a two time scales periodic multi-strain SIS epidemic model:a patchy environment with fast migrations.Ecological Complexity,2012, 10:34–41

[11]McCluskey C C.Complete global stability for an SIR epidemic model with delay-distributed or discrete. Nonl Anal RWA,2010,11:55–59

[12]Muroya Y,Enatsu Y,Kuniya T.Global stability for a class of multi-group SIR epidemic models with patches through migration and cross patch infection.Acta Mathematica Scientia,2013,33B(2):341–361 [13]Thieme H R.Pathogen competition and coexistence and the evolution of virulence//Mathematics for Life Sciences and Medicine.Berlin:Springer,2007:123–153

∗June 13,2014;revised September 19,2015.The†

Yoshiaki MUROYA.

was supported by JSPS KAKENHI Grant Number 15K05010.