RIESZ IDEMPOTENT OF (n,k)-QUASI-∗-PARANORMAL OPERATORS∗

Qingping ZENGCollege of Computer and Information Sciences,Fujian Agriculture and Forestry University, Fuzhou 350002,China E-mail:zqpping2003@163.com

Huaijie ZHONGSchool of Mathematics and Computer Science,Fujian Normal University,Fuzhou 350007,China E-mail:zhonghuaijie@sina.com

RIESZ IDEMPOTENT OF (n,k)-QUASI-∗-PARANORMAL OPERATORS∗

A bounded linear operator T on a complex Hilbert space H is called(n,k)-quasi-∗-paranormal if

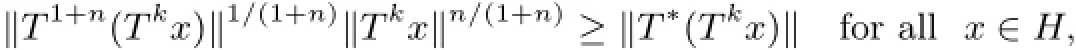
where n,k are nonnegative integers.This class of operators has many interesting properties and contains the classes of n-∗-paranormal operators and quasi-∗-paranormal operators.The aim of this note is to show that every Riesz idempotent Eλwith respect to a non-zero isolated spectral point λ of an(n,k)-quasi-∗-paranormal operator T is self-adjoint and satisfies ranEλ=ker(T−λ)=ker(T−λ)∗.

∗-class A operator;∗-paranormal operator;Riesz idempotent

2010 MR Subject Classification47A10;47B20

1　Introduction

There is a growing interest concerning nonhyponormal operators.Let L(H)be the C∗lgebra of all bounded linear operators on an infinite dimensional complex Hilbert space H. Below we list some of these nonhyponormal operators.Recall that an operator T∈L(H)is aid to behere and henceforth,n,k denote nonnegative integers.

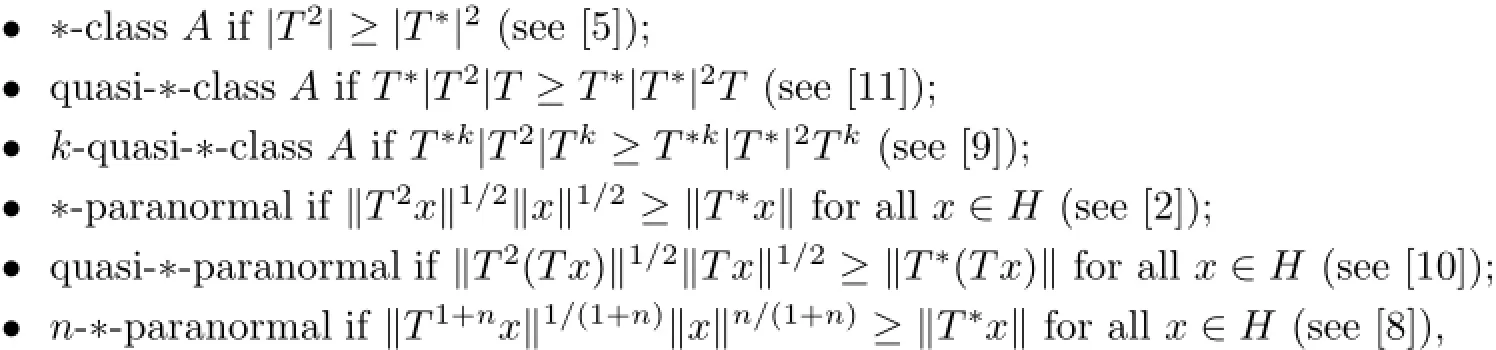
As an extension of the above operator classes,we introduced and studied in[21]the following definition.

Definition 1.1An operator T∈L(H)is said to be(n,k)-quasi-∗-paranormal if

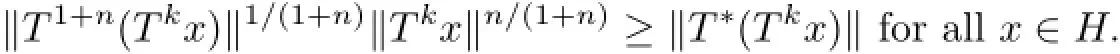
The class of(n,k)-quasi-∗-paranormal operators has many interesting properties(see[21]), such as inclusion relations,SVEP(single valued extension property),matrix representation, joint point spectrum,and so on.

In the present note,we continue to investigate the properties of(n,k)-quasi-∗-paranormal operators.We show that every Riesz idempotent Eλwith respect to a non-zero isolated spectral point λ of an(n,k)-quasi-∗-paranormal operator T is self-adjoint and satisfies ranEλ=ker(T−λ)=ker(T−λ)∗.

2　Riesz Idempotent of(n,k)-Quasi-∗-Paranormal Operators

The self-adjointness of Riesz idempotent with respect to the isolated spectral point of an operator was investigated by a number of mathematicians around the world.For an isolated spectral point λ∈isoσ(T),the Riesz idempotent Eλwith respect to λ is defined by

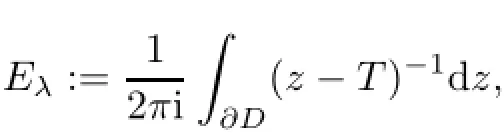
where D is a closed disk with center λ and its radius is small enough such that D∩σ(T)={λ}. In general,the Riesz idempotent Eλis not orthogonal and Eλis orthogonal if and only if Eλis self-adjoint.Stampfli[12]showed that the Riesz idempotent Eλfor an isolated spectral point λ of a hyponormal operator T is self-adjoint.Stampfli’s result was extended to p-hyponormal operators and log-hyponormal operators by Ch¯o and Tanahashi[4],to M-hyponormal operators by Ch¯o and Han[3],to∗-paranormal operators by Tanahashi and Uchiyama[14].In the case λ/=o,Stampfli’s result was extended to p-quasihyponormal operators by Tanahashi and Uchiyama[15],to(p,k)-quasihyponormal operators by Tanahashi,Uchiyama and Ch¯o[16],to w-hyponormal operators by Han,Lee and Wang[6],to class A operators by Uchiyama and Tanahashi[18],to quasi-class A operators by Jeon and Kim[7],to quasi-class(A,k)operators by Tanahashi,Jeon,Kim and Uchiyama[13],to paranormal operators by Uchiyama[17],to k-quasi-∗-class A operators by Mecheri[9].

In this section,we will extend Stampfli’s result to n-∗-paranormal operators and,to(n,k)-quasi-∗-paranormal operators in the case λ/=o.

Theorem 2.1(1)Let T be(n,k)-quasi-∗-paranormal and o/=λ∈isoσ(T).Then the Riesz idempotent Eλis self-adjoint and

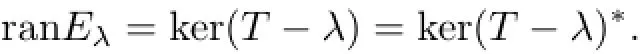
(2)Let T be n-∗-paranormaland λ∈isoσ(T).Then the Riesz idempotent Eλis self-adjoint and

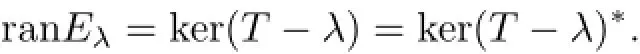
It is worth to note that Theorem 2.1(1)does not hold even for(o,1)-quasi-∗-paranormal (that is,quasi-hyponormal)operators when λ=o(see[15,Example 6]).

To give the proof of Theorem 2.1,we prepare the following lemmas.Recall that an operator T∈L(H)is said to be n-paranormal if‖T1+nx‖1/(1+n)‖x‖n/(1+n)≥‖Tx‖for all x∈H(see [19,2o]).

Lemma 2.2Let T be n-∗-paranormal and λ∈isoσ(T).Then λ is a pole of order one of the resolvent of T.

ProofLet λ∈isoσ(T).Then

By[1,Theorem 3.74],it follows that ranEλ=Ho(T−λ)and kerEλ=K(T−λ),where

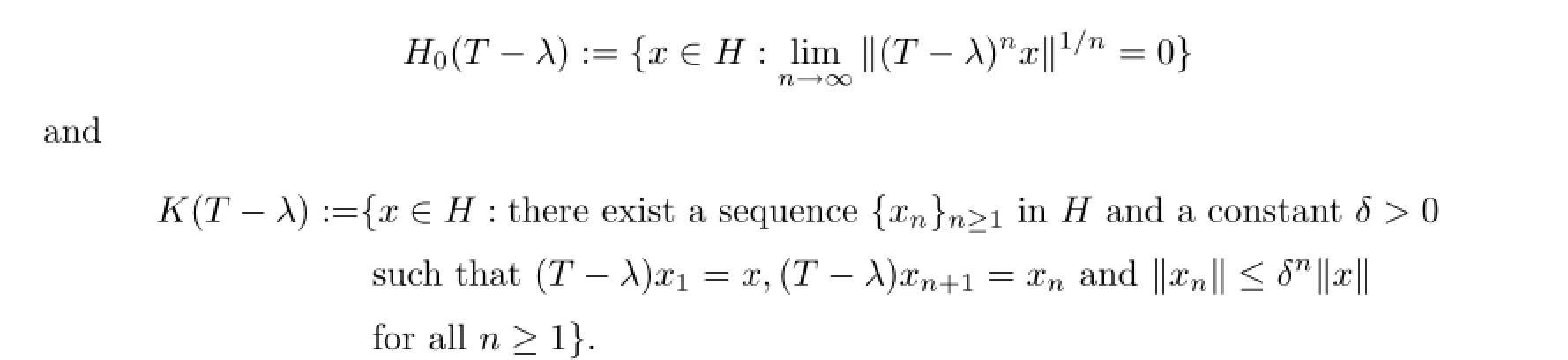
Since T is n-∗-paranormal,it follows from[21]that T is(n+1)-paranormal.Hence by[14, Theorem 2]we have that

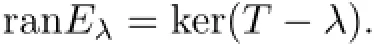
Since H=ranEλ⊕kerEλ,

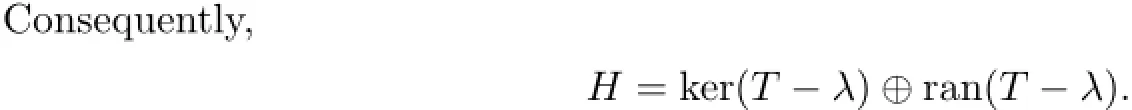
That is,λ is a pole of order one.

Lemma 2.3(see[21])Suppose that ranTkis not dense.Letis the closure of ranTk.If T is(n,k)-quasi-∗-paranormal,then T1is n-∗-paranormal,

Lemma 2.4If T is(n,k)-quasi-∗-paranormal and quasi-nilpotent,then Tk+1=o.

ProofAssume that ranTkis dense,then T is n-∗-paranormal,hence by[21],T is(n+1)-paranormal.Thus by[14,Corollary 1],T=o.So we may suppose that ranTkis not dense. Hence by Lemma 2.3,we can write

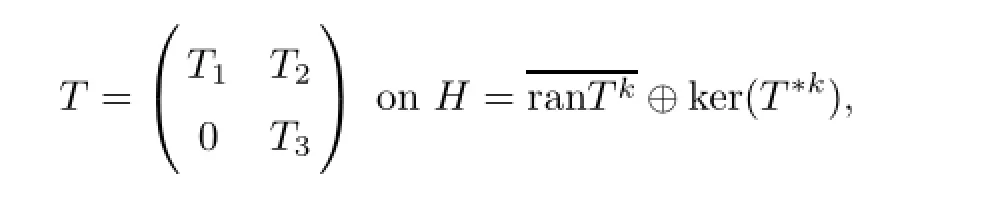
where T1is n-∗-paranormal,σ(T)={o},we see that σ(T)={o}.Hence T=o,and so T=An easy computation yields that

Lemma 2.5Let T be(n,k)-quasi-∗-paranormal and λ∈isoσ(T).Then λ is a pole of the resolvent of T,and the order of λ is no more than k+1 when λ=o,and 1 when λ/=o.

ProofLet λ∈isoσ(T).Then

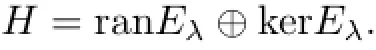
Write T=T1⊕T2with respect to this direct decomposition.Since σ(T1)={λ}and σ(T2)= σ(T){λ},T1−λ is quasi-nilpotent and T2−λ is invertible.

where T11is n-∗-paranormal,={λ}implies that λ=o.It follows from Lemma 2.4 thatand hence λ=o is a pole of order no more than k+1.

Lemma 2.6(see[21])Let T be(n,k)-quasi-∗-paranormal and o/=λ∈ℂ.Then

Proof of Theorem 2.1(1)By Lemma 2.5,λ is an eigenvalue of T,ranEλ=ker(T−λ) and kerEλ=ran(T−λ).Since ker(T−λ)⊆ker(T∗−λ)by Lemma 2.6,ranEλ=ker(T−λ) is a reducing subspace of T.Write T=λ⊕T1with respect to the orthogonal decomposition

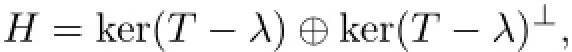
where T1is(n,k)-quasi-∗-paranormal with ker(T1−λ)={o}.Since λ∈isoσ(T)and σ(T)= {λ}∪σ(T1),it then follows from Lemma 2.5 that T1−λ is invertible.Consequently,ker(T−λ)=we have ker(T−λ)⊥ran(T−λ),and hence ranEλ⊥kerEλ.That is,Eλis self-adjoint.

(2)It needs only to consider the case when λ=o.Applying the above argument and using Lemma 2.2 and the fact that ker(T)⊆ker(T∗),the assertion follows.

References

[1]Aiena P.Fredholm and Local Spectral Theory,with Application to Multipliers.Dordrecht:Kluwer Academic Publishers,2004

[2]Arora S C,Thukral J K.On a class of operators.Kyngpook Math J,1986,21(41):381–386

[3]Ch¯o M,Han Y M.Riesz idempotent and algebraically M-hyponormal operators.Integral Equations Operator Theory,2005,53(3):311–320

[4]Ch¯o M,Tanahashi K.Isolated point of spectrum of p-hyponormal,log-hyponormal operator.Integral Equations Operator Theory,2002,43(4):379–384

[5]Duggal B P,Jeon I H,Kim I H.On∗-paranormal contractions and properties for∗-class A operators. Linear Algebra Appl,2012,436(5):954–962

[6]Han Y M,Lee J I,Wang D.Riesz idempotent and Weyl’s theorem for w-hyponormal operators.Integral Equations Operator Theory,2005,53(1):51–60

[7]Jeon I H,Kim I H.On operators satisfying T∗|T2|T≥T∗|T|2T.Linear Algebra Appl,2006,418(2/3): 854–862

[8]Lee M Y,Lee S H,Rhoo C S.Some remark on the structure of k∗-paranormal operators.Kyngpook Math J,1995,35(2):205–211

[9]Mecheri S.Isolated points of spectrum of k-quasi-∗-class A operators.Studia Math,2012,208(1):87–96

[10]Mecheri S.On quasi-∗-paranormal operators.Ann Funct Anal,2012,3(1):86–91

[11]Shen J L,Zuo F,Yang C S.On operators satisfying T∗|T2|T≥T∗|T∗|2T.Acta Math Sinica,Eng Ser, 2010,26(11):2109–2116

[12]Stampfli J G.Hyponormal operators and spectral density.Trans Amer Math Soc,1965,117:469–476

[13]Tanahashi K,Jeon I H,Kim I H,Uchiyama A.Quasinilpotent part of class A or(p,k)-quasihyponormal operators//Oper Theory Adv Appl.Birkh¨auser:Basel,2009,187:199–210

[14]Tanahashi K,Uchiyama A.A note on∗-paranormal operators and related classes of operators.Bull Korean Math Soc,2014,51(2):357–371

[15]Tanahashi K,Uchiyama A.Isolated point of spectrum of p-quasihyponormal operators.Linear Algebra Appl,2002,341(1/3):345–350

[16]Tanahashi K,Uchiyama A,Ch¯o M.Isolated points of spectrum of(p,k)-quasihyponormal operators.Linear Algebra Appl,2004,382:221–229

[17]Uchiyama A.On the isolated points of the spectrum of paranormal operators.Integral Equations Operator Theory,2006,55(1):145–151

[18]Uchiyama A,Tanahashi K.On the Riesz idempotent of class A operators.Math Inequal Appl,2002,5(2): 291–298

[19]Yuan J T,Gao Z S.Weyl spectrum of class A(n)and n-paranormal operators.Integral Equations Operator Theory,2008,60(2):289–298

[20]Yuan J T,Ji G X.On(n,k)-quasiparanormal operators.Studia Math,2012,209(3):289–301

[21]Zeng Q P,Zhong H J.On(n,k)-quasi-∗-paranormal operators.Bull Malays Math Sci Soc,2016,DOI: 10.1007/s40840-015-0119-z

∗October 16,2014;revised March 12,2016.This work has been supported by National Natural cience Foundation of China(11301077,11301078,11401097,11501108)and Natural Science Foundation of Fujian Province(2015J01579,2016J05001).