ASYMPTOTIC SOLUTION OF SINGULARLY PERTURBED HYBRID DYNAMICAL SYSTEMS∗
Limeng WUJuan ZHANGSchool of Mathematics and Information Technology,Hebei Normal University of Science and Technology,Qinhuangdao 066004,China E-mail:neamou123@163.com;wulmmath2010@163.com
Mingkang NIDepartment of Mathematics,East China Normal University,Shanghai 200241,China E-mail:mkni@math.ecnu.edu.cn
Haibo LUSchool of Economics and Management,Shanghai Institute of Technology,Shanghai 201418,China E-mail:classten@163.com
ASYMPTOTIC SOLUTION OF SINGULARLY PERTURBED HYBRID DYNAMICAL SYSTEMS∗
In this paper,we consider a class of optimal control problem for the singularly perturbed hybrid dynamical systems.By means of variational method,we obtain the necessary conditions of the hybrid dynamical systems.Meanwhile,the existence of solution for the hybrid dynamical system is proved by the sewing method and the uniformly valid asymptotic expansion of the optimal trajectory is constructed by the boundary function method.Finally, an example is presented to illustrate the result.
optimal control;hybrid dynamical system;singular perturbation
2010 MR Subject Classification34B15;34E15
1 Introduction
In recent years,optimal control problems of hybrid dynamical systems were successfully investigated by many scholars[1–1o].As we know,the hybrid dynamical systems involve the interaction of both continuous state and discrete state dynamics.In[11]the authors presented a very general optimal control model for hybrid systems and use the dynamic programming to solve the corresponding dynamic programming equations in the form of System of Quasi-Variational Inequalities(SQVI).In[12],the authors showed a more mathematical optimal control model of hybrid dynamical systems.In[13],the authors studied a switched system consisting of subsystems˙x=fi(x,u),i∈I={1,2,···,M},t∈[to,tf].Given a fixed time interval[to,tf]and a prespecified sequence of active subsystems(io,i1,···,ik),find a continuous input u and switching instants t1,t2,···,tksuch that the corresponding continuousstate trajectory x departs from a given initial state x(to)=xoand meets a smooth manifold Sf={x|φf(x)=o,φf:Rn→Rlf}at tfand the cost functional

is minimized,where t1≤t2≤···≤tk≤tf.
In[14],the author considered the singularly perturbed optimal control problem

where x={x1,x2},x1(t)∈Rn1and x2(t)∈Rn2are the state variables,u(t)∈Rmis the control input,and ε>o is a small parameter.By using of the geometric method,the author constructed the high-order asymptotic solution to the optimal state-feedback and the optimal trajectory.In[15],the authors considered the step-like contrast structure for a class of linear singularly perturbed optimal control problem and the uniformly valid asymptotic solution is constructed by the direct scheme method.In[16],the authors developed a new approach to the singularly perturbed time-invariant linear system,which is based on the Chang decoupling transformation.
To our knowledge,asymptotic solution of singularly perturbed hybrid dynamical systems was not investigated.Motivated by the above mentioned papers,the present paper is devoted to consider optimal control of singularly perturbed hybrid dynamical systems.By virtue of variational method and boundary layer function method[17–26],we not only prove the existence of solution for the hybrid dynamical systems,but also construct uniformly valid asymptotic solution to the optimal controller and optimal trajectory.
2 Statement of Problem
We consider the following optimal control problem for singularly perturbed hybrid dynamical systems
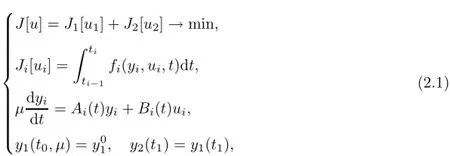
whereµ>o is a small parameter,t∈[to,t2],o=to Let the following assumptions be satisfied: (A1)Assume that fi(yi,ui,t),Ai(t)and Bi(t)are sufficiently smooth on the domain Di={(yi,ui,t)|||yi|| (A2)Assume that there exists unique functionsuch that From(2.2),we can get Defining the functional I(u,λ), From the calculus of variations,we can obtain the first order variation of I(u,λ)as According to the Lagrange theory,a necessary condition for a solution to be optimal is (A3)Assume thato is uniquely solvable with respect to ui,that is ui=hi(yi,λi,t),i=1,2. From assumption(A3)and(2.4),we can get the following singularly perturbed boundary value problem To show the existence of solution for(2.5),we introduce the left and right associated problem with the following boundary value conditions. Left associated problem P(−)(to≤t≤t1) and right associated problem P(+) which satisfy the conditions y2(t1)=y1(t1),λ2(t1)=λ1(t1). By assumption(A2),we obtain that the reduced problem which has a unique solution (A4)Assume that the matrix gixi(¯xi(t),t)has 2n real valued eigenvalues¯λij(t),j= 1,2,···,2n,where According to the boundary function method[18],we suppose that the formal asymptotic series for the boundary value problems(2.6)and(2.7)have the form where τo=tµ−1,τ=(t−t1)µ−1,τ1=(t−t2)µ−1,¯xki(t)are coefficients of regular terms, Lkx1(τo)and Rkx2(τ1)are coefficients of boundary layer terms at t=toand t=t2,Qkxi(τ) are left and right coefficients of internal transition terms at t=t1,i=1,2. Substituting the asymptotic solution(3.1)into(2.6)and(2.7)and separating the terms on t,τo,τ and τ1by the boundary layer function method,then equating the terms with like powers ofµ,we can obtain a series of boundary value problems to determine The equations to determine the zero-order coefficients of regular termsi=1,2 are given by From assumption(A2),we have Next,we give the equations and their conditions for determining the zero order coefficients of left boundary layer and internal transition layer of left side as follows The first order approximation system of(3.3)isUsing assumption(A4),we know that there exists an n dimensional unstable invariant manifold U in the neighborhood ofβ1(t1),t1,we suppose that it can be written as on G1,where G1is some neighborhood of Qoλ1(τ). In order to guarantee the existence of solution for(3.2)and(3.3),we give the following condition. (A5)Assume thatare stable manifold of(3.2)near the equilibrium point β1(to)and Qoλ1(o)=λo−α1(t1)∈G1. The following boundary value problems to determine Qoy2(τ),Qoλ2(τ),Roy2(τ2), and Roλ2(τ2)are given by Similarly,we know that there exists an n dimensional stable invariant manifold S in the neighborhood of?β2(t1),t1?,we suppose that it can be written as on G2,where G2is some neighborhood ofare unstable manifold of(3.5)near the equilibrium point β2(t2)and Qoy2(o)=po−φ2(t1)∈G2. For the high order terms of P(−),we have the equations and their boundary conditions as follows:are the known functions depending only on¯xp1(t),Lpx1(τo),Qpx1(τ)and tp(p=o,1,2,···,k−1).Consider equations(3.8),they are first order linear inhomogeneous differential equations,the inhomogeneous term QFk(τ)is a known vector functions.The homogeneous equations of(3.8)are variational equations of(3.3).Therefore,by the result of Vasil’eva,Butuzov[21],we obtain that there exists a unique solution Qkx1for(3.8),meanwhile, where δkis a determined constant depending on Φ1,QFk(τ),C and kpare positive constants. Similarly,we can get the left boundary layer terms Lkx1(τo),so far we constructed the asymptotic solution of P(−). For the high order approximate equation of Qkx2(τ),the initial condition for the existence of a unique solution is where σkis a known constant. Similar to the above discussion,we can get the equations and boundary conditions to determine right boundary layer coefficients Rkx2(τ1),here the details are omitted.Then,we have thus far constructed the formal asymptotic solution for the problems P(−)and P(+).By means of the expressions yi,λiand ui=hi(yi,λi,t),the asymptotic expansion of ui,i=1,2 can be obtained.It should be noted that the formal asymptotic solution contains the unknown parameters λ∗and p∗. Next,we will determine the vector parameters λ∗and p∗by continuity of solution,that is then equating the terms with like powers ofµ,we obtain the following equations Equating the terms with like k-th powers ofµ,we get the equations In order to ensure that there exist solutions for equations(3.1o)and(3.11),the following assumptions are needed. (A7)Assume that there exists a unique solution for the vector equations (A8)Assume that the matrices E−AB and E−BA are invertible. By virtue of(A8),the unknown parameters pkand λkcan be solved from(3.11),.So far,we have determined all the parameters pkand λk,k≥1. We will use the sewing method to prove the existence of solution for(2.5),meanwhile, the asymptotic expansion will be given.Let x∗=xo+µx1+···+µNxN,here,we do not expand xN,the purpose is to prove the existence of xN,then we will prove the existence for x∗.Consider the difference value function Let the right hand side of above equation be equal to zero,we can obtain here,△x|t=t1=o,that is,the value of asymptotic solutions for P(−)and P(+)are equal at the point t1. In[21],the authors proved the existence of solution for the two point boundary value problem,which satisfies the stability condition.Moreover,the authors showed the uniformly valid asymptotic solution for the boundary value problem.In this paper,we divide problem (2.5)into two boundary value problems,which satisfy the stability conditions.Then,we have the following theorem Theorem 4.1Assume that(A1)–(A8)hold.Then,for sufficiently smallµ>o,there exists a unique solution x(t,µ)for(2.1).Moreover,the following asymptotic expansion holds Consider the following optimal control problem whereµ>o is a small parameter. By using the optimality condition of optimal control problem(5.1),we have The equations and conditions to determine Qoy1and Qoλ1are given by For Qoy2and Qoλ2,we have the equations and boundary conditions as follows By means of y2(1)=y1(1),λ2(1)=λ1(1),we obtain that Similarly,we get From the optimality condition,we know that u1+λ1=o,u2+λ2=o,then we have the asymptotic solution for(5.1), [1]Witsenhausen H S.A class of hybrid-state continuous-time dynamic systems.IEEE Trans Automatic Cont, 1966,11(6):665–683 [2]Cellier F E.Combined Continuous/Discrete System Simulation by Use of Digital Computer:Techniques and Tools.Switzerland Zurich:Swiss Federal Institute of Technology,1979 [3]Michel A N,Hu B.Towards a stability theory of general hybrid dynamical systems.Automatica,1999, 35(3):371–384 [4]Yong J M.Systems governed by ordinary differential equations with continuous switching and impulse controls.Appl Math Opti,1989,20:223-235 [5]Branicky M S.Multiple Lyapunov functions and analysis tools for switched and hybrid systems.IEEE Transactions on Automatic Control,1998,34(4):475–482 [6]Mo Y W,Xiao D Y.Overview of hybrid dynamic system and its application.Contr Theory Appl,2002, 19(1):1–8 [7]Guo L,Yu R L,Tian F Z.Optimal control of one kind general jump transition system.Journal of Shandong University,2006,41(1):35–40(in Chinese) [8]Zhu F,Antsaklis P J.Optimal control of hybrid switched systems:a brief survey.Discrete Event Dynamics Systems:Theory and Applications,2015,25:345–364 [9]Marzbann H R,Hoseini S M.A hybrid approximation scheme for discretizing constrained quadratic optimal control problems.J Franklin Inst,2014,351:2640–2656 [10]Lee T.Optimal control of partitioned hybrid systems via discrete-time Hamilton-Jacobi theory.Automatica, 2014,50:2062–2069 [11]Branicky M S,Borkar V S,Mirtter S K.A unified framework for hybrid control:model and optimal control theory.IEEE Trans Automatic Cont,1998,43(1):31–45 [12]Bensoussan A,Memaldi J L.Hybrid control and dynamic programming.Dynamics of Continuous,Discrete and Impulsive Systems,1997,3:395–442 [13]Xu X P,Antsaklis P J.Optimal control of switched systems based on parameterization of the switching instants.IEEE Trans Automatic Cont,2004,49(1):2–16 [14]Fridman E.Exact slow-fast decomposition of the nonlinear singularly perturbed optimal control problem. Syst Control Lett,2000,40:121–131 [15]Ni M K,Dmitriev M G.Steplike contrast structure in an elementary optimal control problem.Comput Math Math Phys,2010,50(8):1312–1323 [16]Koskie S,Coumarbatch C,Gajic Z.Exact slow-fast decomposition of the singularly perturbed matrix differential Riccati equation.Applied Mathematics and Computation,2010,216:1401–1411 [17]Ni M K,Lin W Z.Minimizing sequence of variational problems with small parameters.Applied Mathematics and Mechanics,English Edition,2009,30(6):695–701 [18]Ni M K,Dmitriev M G.Contrast structures in the simplest vector variational problem and their asymptotics.Avtomatika i Telemekhanika,1998,5:41–52 [19]Vasil’eva A B,Dmitriev M G,Ni M K.On a step-like contrast structure for a problem of the calculus of variations.Comput Math Math Phys,2004,44(7):1203–1212 [20]Kokotovic P,Khalil H,O’Reilly J.Singular Perturbation Methods in Control:Analysis and Design.Orlando: Academic Press,1986 [21]Vasil’eva A B,Butuzov V F.Asymptotic Expansions of Singularly Perturbed Differential Equations. Moscow:Nauka,1973 [22]Barbu L,Morosanu G.Singularly Perturbed Boundary-Value Problems.Basel,Boston,Berlin:Birkhauser, 2007 [23]Vasilieva A B,Butuzov V F,Kalachev L V.The Boundary Function Method for Singular Perturbation Problems.Philadelphia:SIAM,1995 [24]Wang A F,Ni M K.The interior layer for a nonlinear singularly perturbed differential difference equation. Acta Mathematica Scientia,2012,32B(2):695–709 [25]Xie F.Singular perturbation for a class of reaction diffusion equation.Acta Mathematica Scientia,2003, 23A(3):369–373(in Chinese) [26]Mo J Q,Wang H,Lin W T.The solvability for a class of singularly perturbed quasi-linear differential system.Acta Mathematica Scientia,2008,28B(3):495–500 ∗December 6,2014;revised April 25,2016.This project is supported by the National Natural Science Foundation of China(11471118,11401385 and 11371140),Natural Science Foundation of Hebei Province (A2015407063)and Doctoral Foundation of Hebei Normal University of Science and Technology(2013YB008).

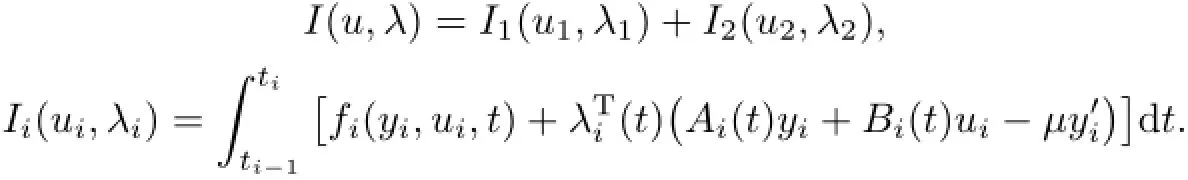

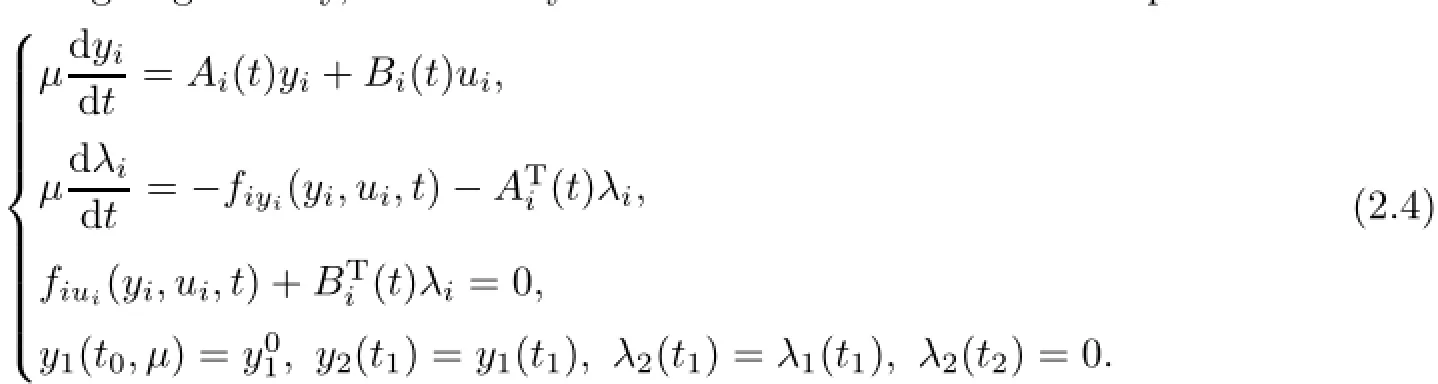
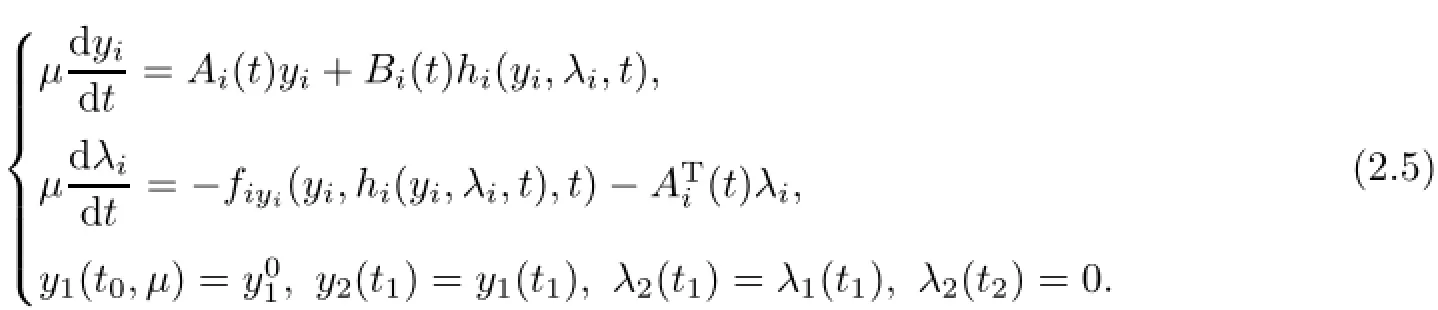
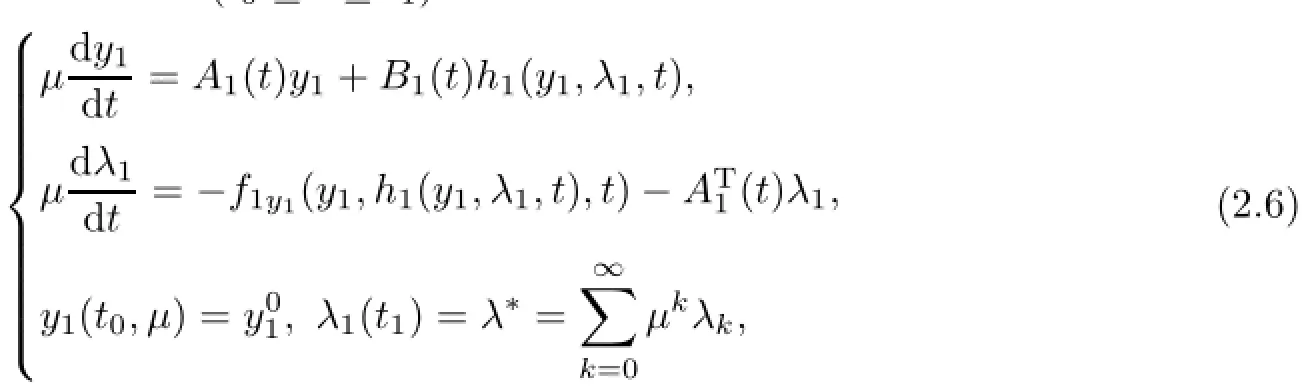
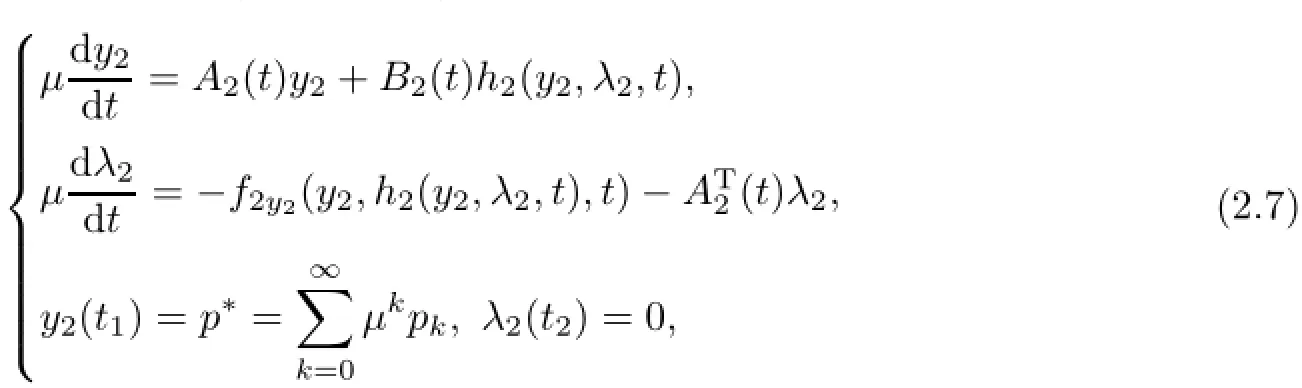
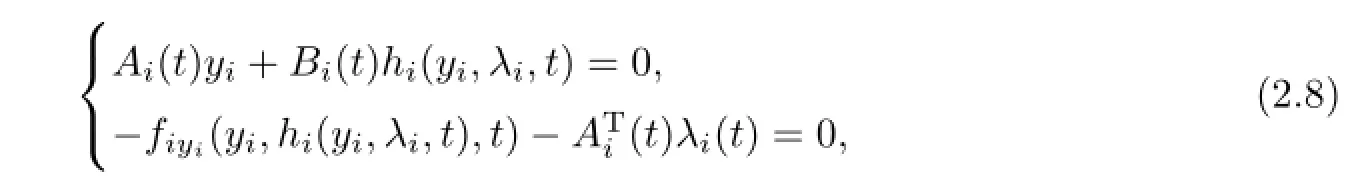
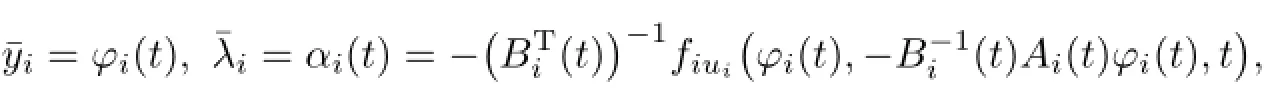
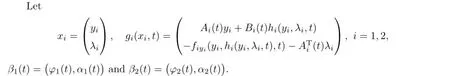

3 Construction of Asymptotic Solution
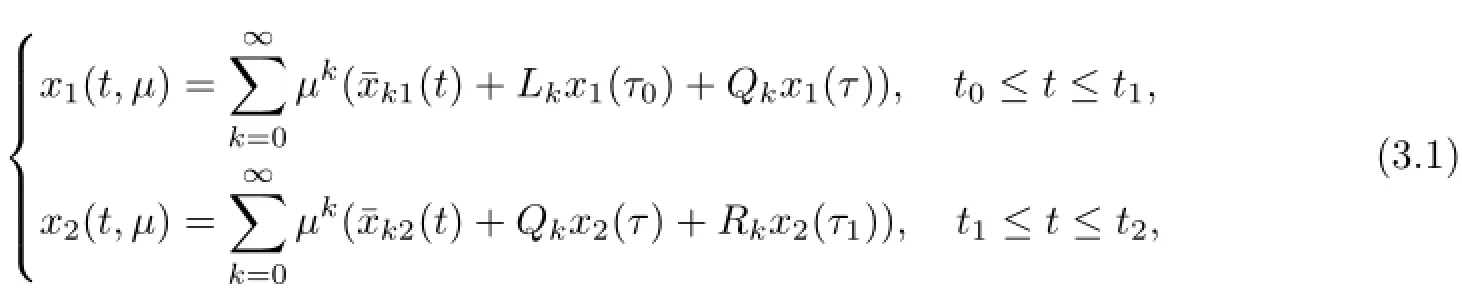
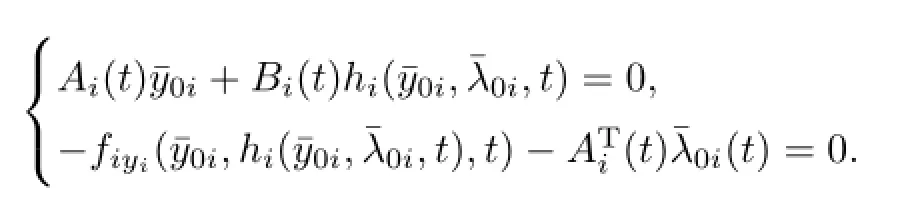
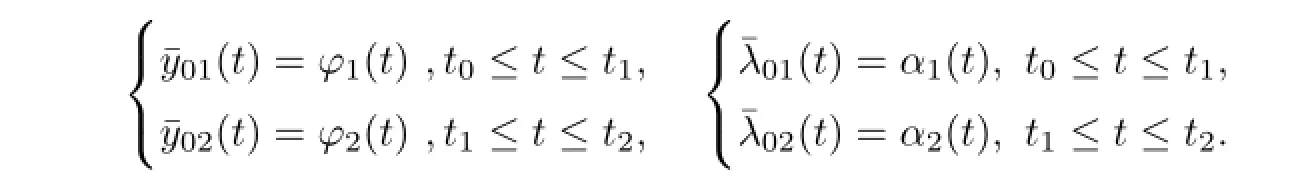

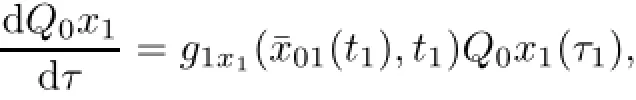

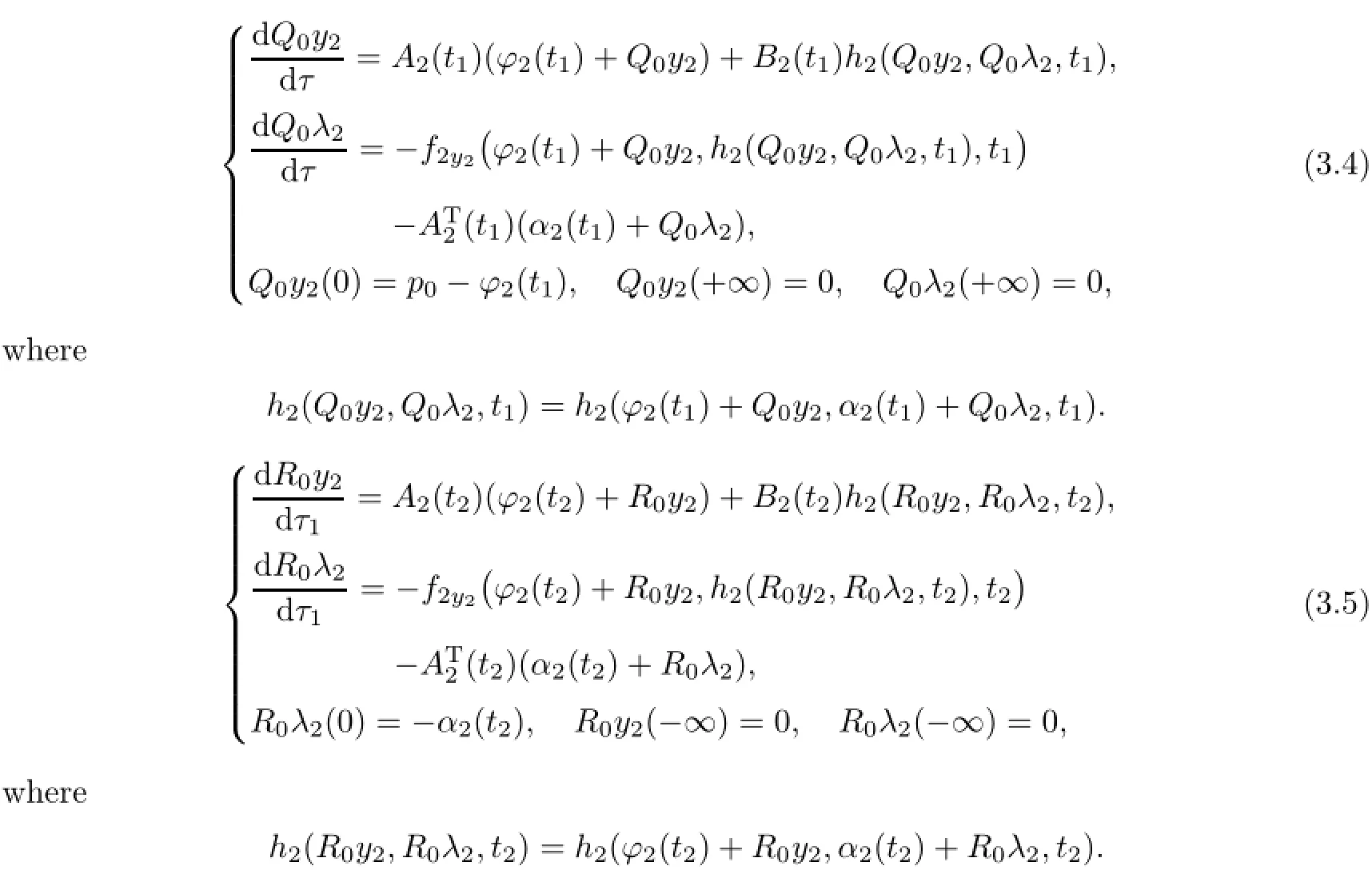
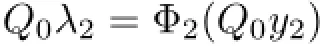
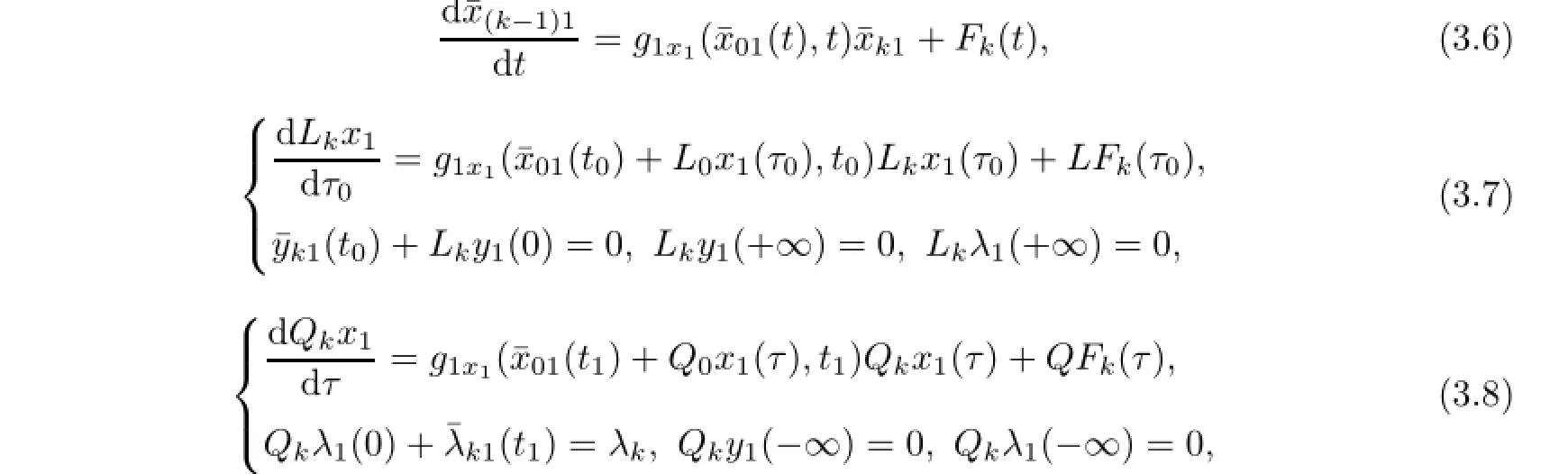
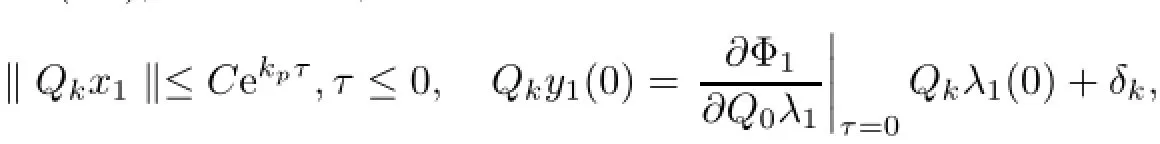
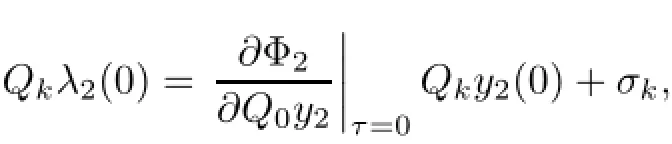
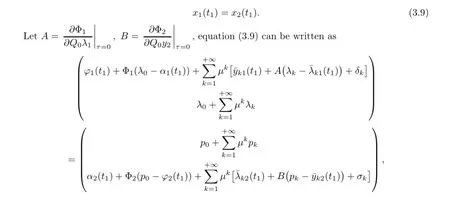
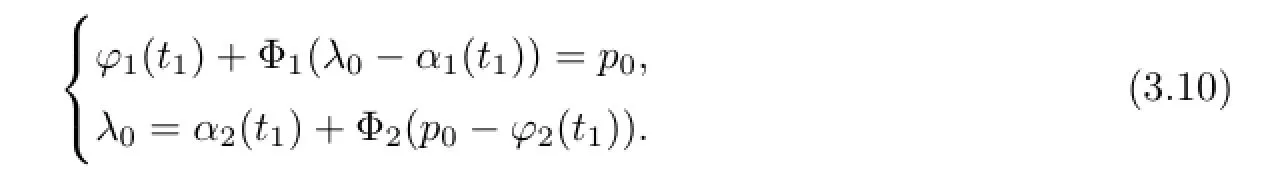

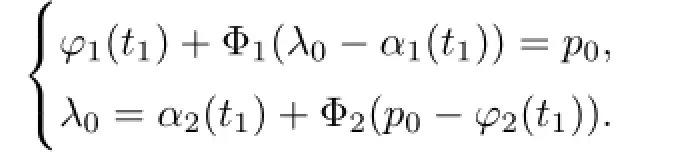
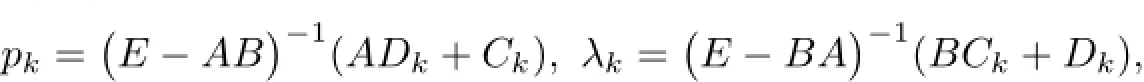
4 Existence and Formal Asymptotic Expansion for Solution
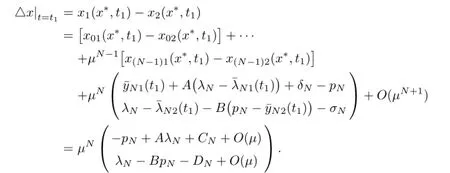
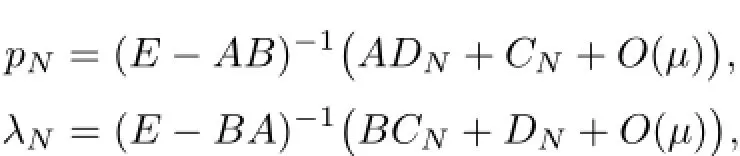

5 Example
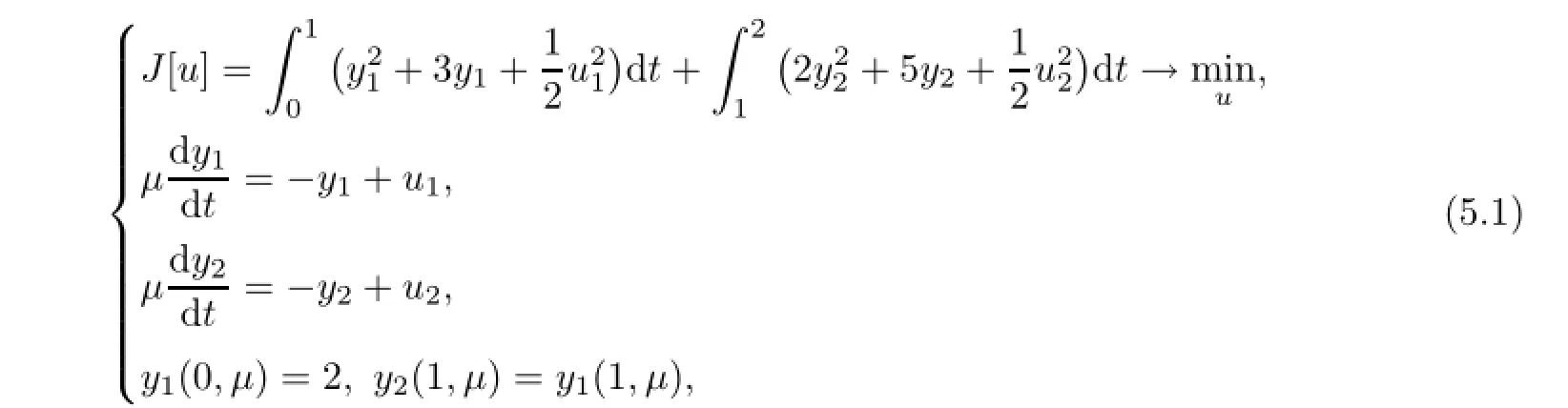
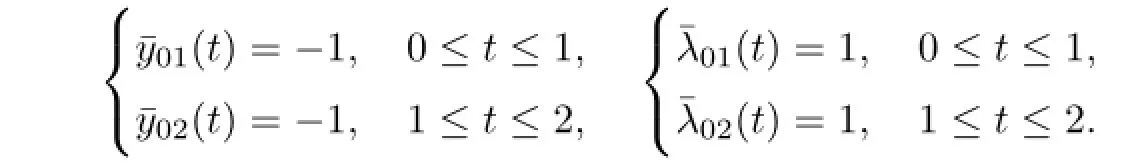
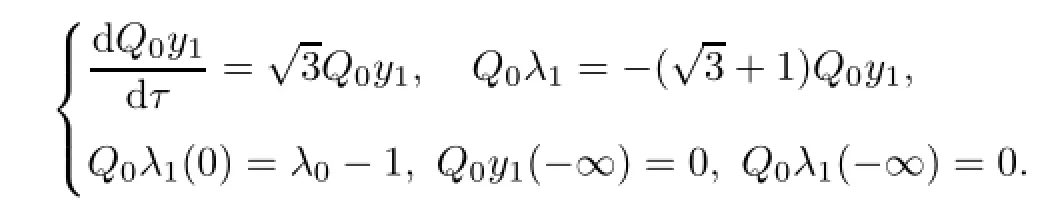
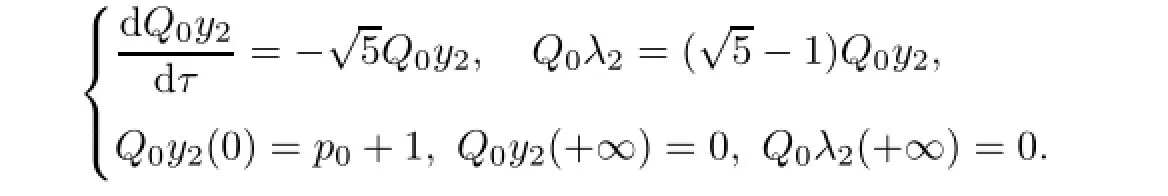
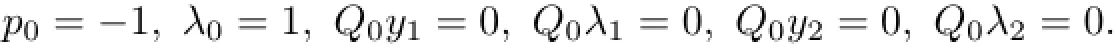
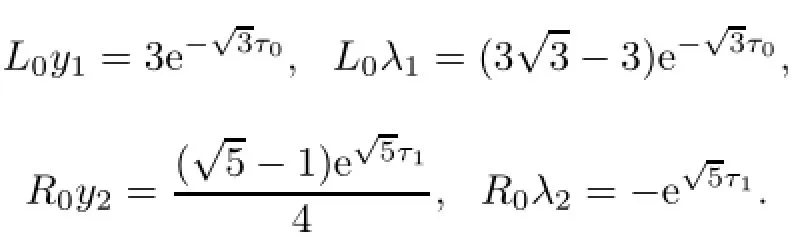
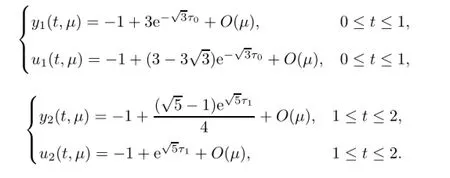
References
 Acta Mathematica Scientia(English Series)2016年5期
Acta Mathematica Scientia(English Series)2016年5期
