WANDERING SUBSPACES OF THE HARDY-SOBOLEV SPACES OVER Dn∗
Jiesheng XIAONanhu College,Jiaxing University,Jiaxing 314001,China Department of Mathematics,Sun Yat-sen University,Guangzhou 510275,China E-mail:xiaojiesheng@126.com
Guangfu CAODepartment of Mathematics,South China Agricultural University,Guangzhou 510642,China E-mail:guangfucao@163.com
WANDERING SUBSPACES OF THE HARDY-SOBOLEV SPACES OVER Dn∗
In this paper,we show that forsuppose S is an invariant subspace of the Hardy-Sobolev spacesfor the n-tuple of multiplication operators (Mz1,···,Mzn).If(Mz1|S,···,Mzn|S)is doubly commuting,then for any non-empty subset α={α1,···,αk}of{1,···,n},WαSis a generating wandering subspace for Mα|S=
wandering subspace;invariant subspace;Beurling’s theorem;Hardy-Sobolev space;doubly commuting
2010 MR Subject Classification47A15
1 Introduction
A closed subspace W of a Hilbert space H is said to be a generating wandering subspace (see[4])for a n-tuple T=(T1,···,Tn)of commuting bounded linear operators on H if
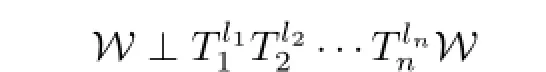
for all(l1,···,ln)∈ℕn{(o,···,o)}and
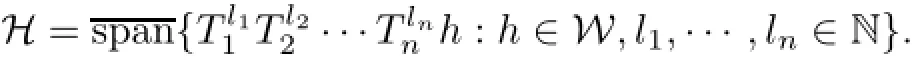
In this case,the tuple T is said to have the generating wandering subspace property.
Let(T1,···,Tn)be a commuting n-tuple of bounded linear operators on a Hilbert space H.Does there exist a generating wandering subspace W for(T1,···,Tn)?
This question has an affirmative answer for the restriction of the co-ordinate multiplication operator Mz,to an invariant subspace of the Hardy space H2(D).In[2],Beurling proved that ifS/=o is an Mz-invariant subspace of the Hardy space H2(D),then S⊖zS is a one dimensional subspace spanned by an inner function η and
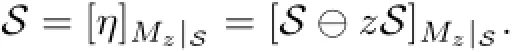
Beurling’s theorem played an important role in operator theory,function theory and their intersection,function-theoretic operator theory.However,despite the great development in these fields over the past fifty years,it is only recently that progress was made in proving analogues for the other classical Hilbert spaces,the Dirichlet space and the Bergman space. In[8],Richter proved that the analogue of Beurling’s theorem is true in the Dirichlet space D(D).It is well known that the invariant subspace lattice of the Bergman spaceis very complicated.In fact,the dimension of the wandering subspace S⊖zS can be an arbitrary positive integer or∞(see[5]).However,a big breakthrough in the study of the analogue of Beurling’s theorem on the Bergman space was made by Aleman,Richter and Sundberg(see [1]).They proved that any invariant subspace S of the Bergman spacealso has the generating wandering subspace property.
In[9],Rudin showed that there are invariant subspaces M of H2(D2)which do not contain any bounded analytic function.In particular,for n≥2 the Beurling’s theorem like characterization of(Mz1,···,Mzn)-invariant subspaces of H2(Dn),in terms of inner functions on Dn, is not possible.Moreover,existence of generating wandering subspaces for general invariant subspaces of the Hardy space H2(Dn)rather fails spectacularly.
We now recall the following definition,we say that a closed subspace M of Hilbert space H is invariant for a n-tuple of operators(T1,···,Tn),if TiM⊂M for all i=1,···,n.We say that a commuting n-tuple(T1,···,Tn)(n≥2)of bounded linear operators on H is said to be doubly commuting if
Let H(Dn)denote the set of all holomorphic functions on Dn,let H⊆H(Dn)be a reproducing kernel Hilbert space such that the multiplication operators{Mz1,···,Mzn}by the co-ordinate functions are bounded.Then a closed(Mz1,···,Mzn)-invariant subspace S of H is said to be doubly commuting if the n-tuple(Mz1|S,···,Mzn|S)is doubly commuting,that
In[11],Sarkar et al.proved that any doubly commuting invariant subspace of H2(Dn) (where n≥2)has the generating wandering subspace property(see[6]for n=2).Also in[7], Redett and Tung obtained the analogue conclusion for doubly commuting invariant subspacesRecently,in[3],Chattopadhyay et al.proved that doubly commuting invariant subspaces of the Bergman spaceand the Dirichlet space D(Dn) have the generating wandering subspace property.
Motivated by the work of[3],in this paper we will consider the generating wandering subspace property for doubly commuting invariant subspaces of the Hardy-Sobolev spaces over Dn.
Recall that the Hardy space over the unit polydisc
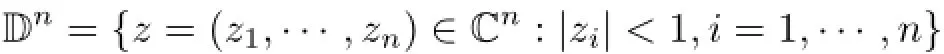
is denoted by H2(Dn)and defined by

where dθ is the normalized Lebesgue measure on the torus Tn,the distinguished boundary of Dn,rz:=(rz1,···,rzn)(see[9,12]).
For β∈R,the Hardy-Sobolev spacesconsists of analytic functions f in Dnso that Rβf∈H2(Dn),is the Taylor expansion of f and
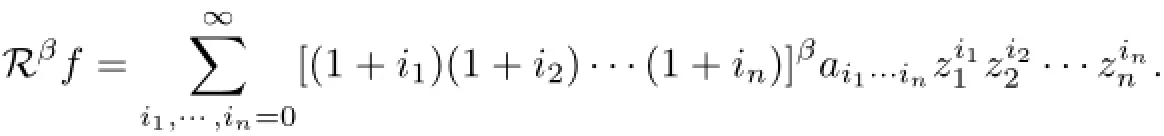
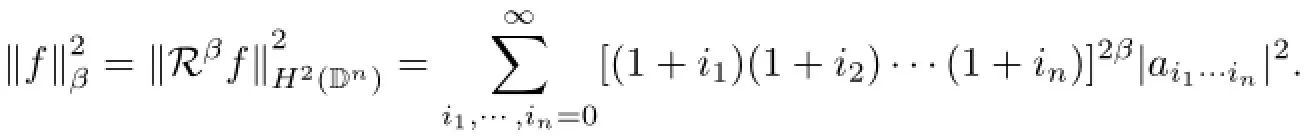
We fix for the rest of the paper a natural number n≥2 and set Λn:={1,···,n}.For a closed subset K of a Hilbert space H,a n-tuple of commuting operators T=(T1,···,Tn)on H and a non-empty subset α={α1,···,αk}⊆Λn,we write[K]Tαto denote the smallest closed joint Tα:=(Tα1,···,Tαk)-invariant subspace of H containing K.In other words,

We denote by M=(Mz1,···,Mzn)the n-tuple of co-ordinate multiplication operators onand non-empty set α={α1,···,αk}⊆Λn,
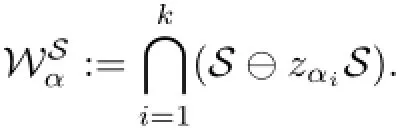
The following is our main result.
If(Mz1|S,···,Mzn|S)is doubly commuting,then for any non-empty subset α={α1,···,αk}generating wandering subspace for Mα|S=(Mzα1|S,···,Mzαk|S),that is,
2 Proof of Main Result
A bounded linear operator T on a Hilbert space H is said to be analytic if
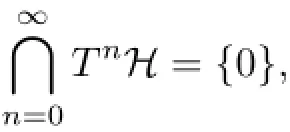
and concave if it satisfies the following inequality
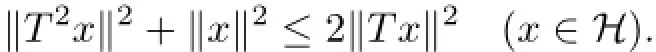
For a single bounded operator T on a Hilbert space H,the following result ensures the generating wandering subspace property for T under certain conditions.
Theorem 2.1(see[8,1o])Let T be an analytic operator on a Hilbert space H which satisfies one of the following properties:
(i)‖Tx+y‖2≤2(‖x‖2+‖Ty‖2)(x,y∈H).
(ii)T is concave.
Then H⊖TH is a generating wandering subspace for T,that is,H=[H⊖TH]T.
Recently,Chattopadhyay et al.[3,Corollary 2.4]proved a multivariate version of Theorem 2.1 for a class of doubly commuting operators as following.
Theorem 2.2(see[3])Let T=(T1,···,Tn)be a commuting tuple of analytic operators on H such that T is doubly commuting and satisfies one of the following properties:
(a)Tiis concave for each i=1,···,n.
(b)‖Tix+y‖2≤2(‖x‖2+‖Tiy‖2)(x,y∈H,i=1,···,n).
Then for any non-empty subset α={α1,···,αk}⊆Λn,Wαis a generating wandering subspace
The following two lemmas are very useful in our proof.
ProofWithout loss of generality,we assume that i=1,so we only need to prove that
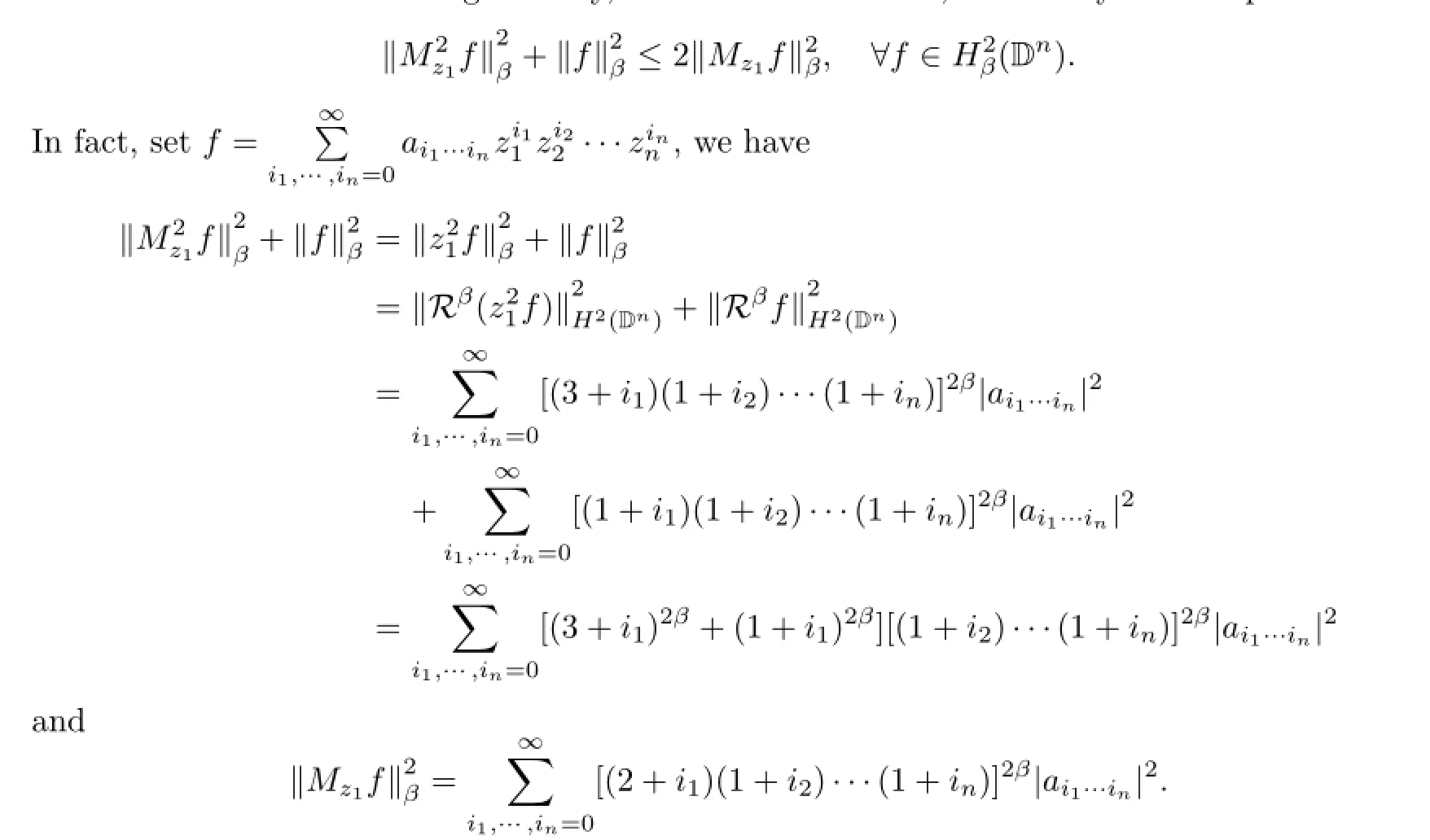
Write k=1+i1and t=2β,thus k≥1 and o≤t≤1.Now we only need to prove that

and we complete the proof of the lemma.
If t=o,it is clear that(2.1)follows.
If o Therefore,for o we have(2+k)t+kt≤2(1+k)t.This completes the proof. ProofWithout loss of generality,we assume that i=1,so we only need to prove that On the other hand,we get In order to prove inequality(2.2),by comparing(2.3)and(2.4),we only need to prove following (2.5)and(2.6). Next,write t=2β.In order to prove inequality(2.6),we only need to prove that for any integer i1≥1 and then(2.7)follows. We claim that for any integer i1≥1 and≤t which is equivalent to(2.8). In fact,fix i1≥1,since the functions G(x)=(x+i1)tand H(x)=(x+i1+1)tis derivable on the interval[o,1].By the Cauchy mean value theorem,then there exists a ζ∈[o,1]such that This implies that the rigth of(2.9)is equal to Hence we have that for the claim follows.This means that(2.5)and(2.6)follow.The proof is completed. We are now ready to prove the main result. Proof of Theorem 1.1The theorem follows if we show that the tuple of operators on S satisfies the hypothesis of Theorem 2.2.In fact,it is well known that the co-ordinate multiplication operator Mzionis analytic for all i=1,···,n.Then Mzi|Sis also analytic for all i=1,···,n.By Lemmas 2.3 and 2.4,we see that foreither condition(a)or(b)of Theorem 2.2,holds.Thus,by Theorem 2.2 we have that The proof is completed. Remark 2.5By the definition of the Hardy-Sobolev spacesa direct calcula-for all 1≤i then(Mz1|S,···,Mzn|S)is not doubly commuting. Remark 2.6It is easy to see that.By the proof of Lemma 2.4,indeed,for t=−1,that is,β=inequality(2.8)also holds,we have that Lemma 2.4 follows.Hence, Theorem 1.1 holds. We finish this paper with the following natural question. Question 2.7 whether Theorem 1.1 also holds? [1]Aleman A,Richter S,Sundberg C.Beurling’s theorem for the Bergman space.Acta Math,1996,177: 275–310 [2]Beurling A.On two problems concerning linear transformations in Hilbert space.Acta Math,1949,81: 239–255 [3]Chattopadhyay A,Das B,Sarkar J,Sarkar S.Wandering subspaces of the Bergman space and the Dirichlet space over Dn.Integr Equ Oper Theory,2014,79:567–577 [4]Halmos P R.Shifts on Hilbert spaces.J Reine Angew Math,1961,208:102–112 [5]Hedenmalm H.An invariant subspace of the Bergman space having the codimension two property.J Reine Angew Math,1993,443:1–9 [6]Mandrekar V.The validity of Beurling theorems in polydiscs.Proc Amer Math Soc,1988,103:145–148 [7]Redett D,Tung J.Invariant subspaces in Bergman space over the bidisc.Proc Amer Math Soc,2010,138: 2425–2430 [8]Richter S.Invariant subspaces of the Dirichlet shift.J Reine Angew Math,1988,386:205–220 [9]Rudin W.Function Theory in Polydiscs.New York:Benjamin,1969 [10]Shimorin S.Wold-type decompositions and wandering subspaces for operators close to isometries.J Reine Angew Math,2001,531:147–189 [11]Sarkar J,Sasane A,Wick B.Doubly commuting submodules of the Hardy module over polydiscs.Studia Math,2013,217:179–192 [12]Wang X F,Cao G F.Galerkin-Petrov methods of Toeplitz operators on Dirichlet space.Acta Math Sci, 2007,27B(2):308–317 ∗January 22,2015;revised March 23,2016.This work was partially supported by the Natural Science Foundation of China(11271092,11471143),the key research project of Nanhu College of Jiaxing University (N41472001-18).† Jiesheng XIAO.
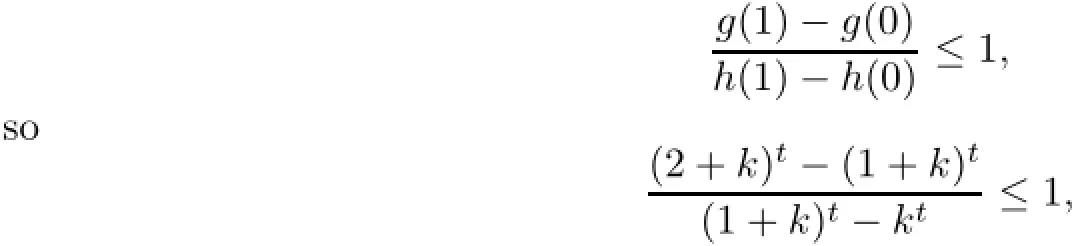


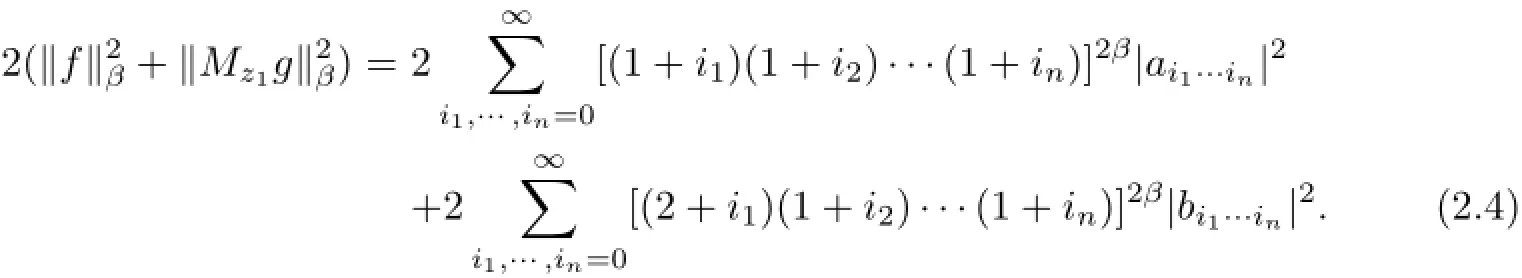
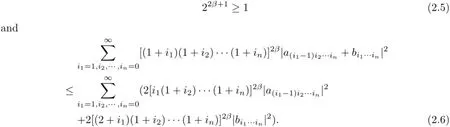

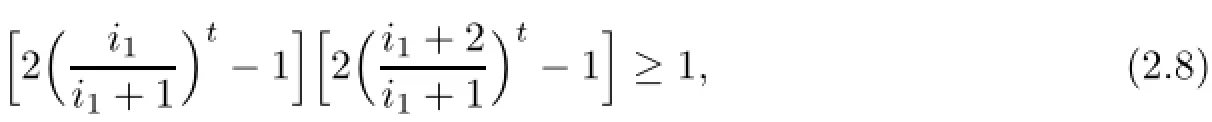

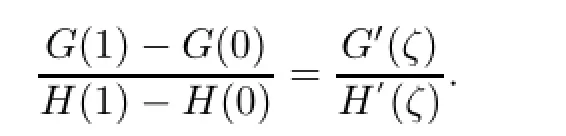
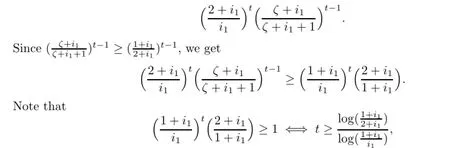
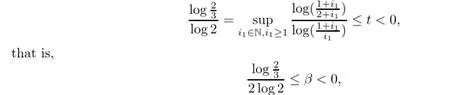

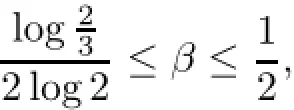
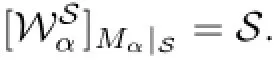
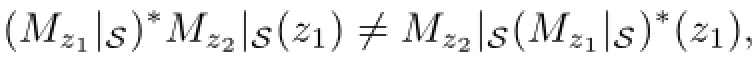
References
 Acta Mathematica Scientia(English Series)2016年5期
Acta Mathematica Scientia(English Series)2016年5期
