SOLVABILITY OF A PARABOLIC-HYPERBOLIC TYPE CHEMOTAXIS SYSTEM IN 1-DIMENSIONAL DOMAIN∗
Hua CHENWenbin LShaohua WUSchool of Mathematics and Statistics; Computational Science Hubei Key Laboratory,Wuhan University,Wuhan 430072,China E-mail:chenhua@whu.edu.cn;lvwenbin@whu.edu.cn;wush8@sina.com
SOLVABILITY OF A PARABOLIC-HYPERBOLIC TYPE CHEMOTAXIS SYSTEM IN 1-DIMENSIONAL DOMAIN∗
In this paper,we use contraction mapping principle,operator-theoretic approach and some uniform estimates to establish local solvability of the parabolic-hyperbolic type chemotaxis system with fixed boundary in 1-dimensional domain.In addition,local solvability of the free boundary problem is considered by straightening the free boundary.
parabolic-hyperbolic system;free boundary;chemotaxis model;local existence
2010 MR Subject Classification35A01;35K57;35M10;35L10;47D03
1 Introduction
Isolated from decaying leaves collected in a hardwood forest of the North Carolina mountains in the summer of 1933,the cellular slime mold Dictyostelium discoideum was discovered by Raper in 1935[18].
During its life cycle a myxamoebae population of the Dictyostelium grows by cell division as long as there is sufficient nutriment.When the food resources become rare,the myxamoebae spread over the entire domain available to them.After a while one cell starts to secrete cyclic Adenosine Monophosphate(cAMP)which create a chemical gradient attracting the other myxamoebae.The myxamoebae begin to move towards the so-called founder cell and are also stimulated to exude cAMP.At this stage a collective behavior takes place during which these organisms aggregate and start to differentiate.At the end of the aggregation the myxamoebae form a pseudoplasmoid,with each cell maintaining its individual integrity.This self-organized multicellular structure increases in fact the chance of survival with the lack of food.This pseudoplasmoid moves then towards light sources,after a time a fruiting body is formed,spores are spread and the cycle begins again[16].
The aggregation of the Dictyostelium is a typical example of a chemotaxis process(from the Greek Chemo=chemical,taxis=arrangement),which may be defined as the influence of chemical substances on the movement of mobile species.This can lead to strictly orientedmovement or to partially oriented and tumbling movement.The movement towards a higher (resp.lower)concentration of the chemical substance is termed positive chemotaxis movement (resp.negative).
Understanding of the partially oriented movement of cells in response to chemical signals, chemotaxis,is of great significance in various contexts.
In those days it was hard for Raper to imagine,that more than many years later this discovery would have attracted a large group of mathematicians[1,4–8,12,14,15,2o,24,27–29,31]to lay their scientific focus on a model proposed by Keller and Segel[19]in 197o to describe the aggregation phase of the Dictyostelium discoideum.
Suzuki[25]discussed the chemotaxis model

carefully,where Ω⊂ℝnis a bounded domain with smooth boundary∂Ω,n is the outer unit vector on∂Ω,and f=lnW stands for the potential of the outer force,W=W(x)>o is a smooth function of x∈Ω.Here u=u(x,t)and v=v(x,t)are unknown functions of (x,t)∈Ω×[o,T)and they stand for the density of cellular slime molds and the concentration of chemical substances secreted by themselves,respectively.The operator A can be−Δ+a with the Neumann boundary condition,where a>o is a constant.It may be−Δ with the Neumann boundary condition under the constraintRΩ·dx=o,that is,vt+Av=u if and only if
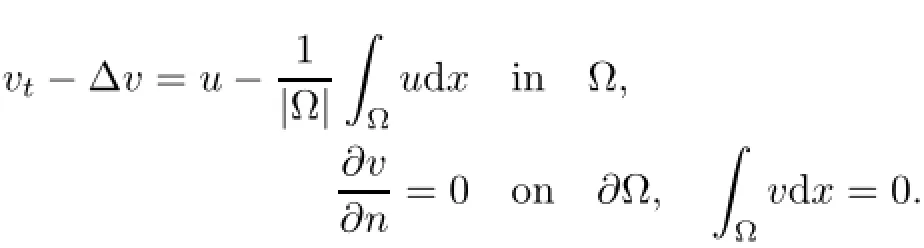
In the third case,it is−Δ with the Dirichlet boundary condition.These cases were studied by [9,17,21].
Suzuki studied the classical theory for this system in his book.First,the fundamental theorem,the unique existence of the solution locally in time,was proved in Chapter 3.Then the threshold for the existence of the solution globally in time,which was eventually explained in a unified way by the quantized blowup mechanism,was established in Chapters 4 and 5.
Chen and Wu[1,3]studied the following parabolic-hyperbolic type chemotaxis system:
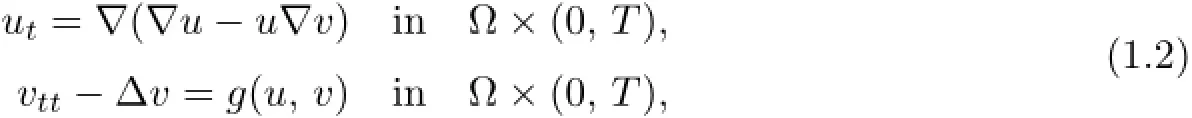
here the hyperbolic equation describes the property of the field generated by the external stimulus,the light or the electromagnetic wave.The results of[1,3]gave the existence and uniqueness of the solution for the system with Neumann boundary value condition on a smoothly bounded open domain.
In this paper,we replace the control equation(the second equation of system(1.1))by a hyperbolic equation
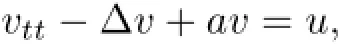
where a>o is a constant.
As we all know,in a standard setting for many partial differential equations,we usually assume that the process being described occurs in a fixed domain of the space.But in the real world,the following phenomenon may happen.At the initial state,a kind of amoeba occupied some areas.When foods become rare,they begin to secrete chemical substances on their own. Since the biological time scale is much slower than the chemical one,the chemical substances are full filled with whole domain and create a chemical gradient attracting the cells.In turn, the areas of amoeba may change according to the chemical gradient from time to time.In other words,a part of whose boundary is unknown in advance and that portion of the boundary is called a free boundary.In addition to the standard boundary conditions that are needed in order to solve the PDEs,an additional condition must be imposed at the free boundary.One then seeks to determine both the free boundary and the solution of the differential equations. The theory of free boundaries saw great progress in the last thirty years;for the state of the field we refer to[1o].
Chen and Wu[2]studied the free boundary value problem and established the existence and uniqueness of the solution of system(1.2)with one dimensional space in some suitable conditions(one of them reads that the mass flow ratio is a positive constant).However,to the best of our knowledge,no results are available for the mass flow ratio being a non-constant coefficient.In the present paper,we consider the corresponding problem with the mass flow ratio to be a positive function.In view of the biological relevance,we find it worthwhile to clarify these questions.
2 Main Results
In this paper,we focus on the following system:
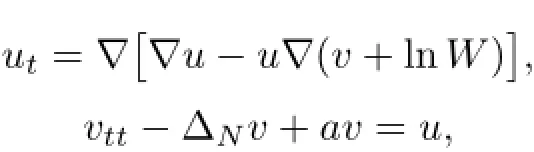
where ΔNdenotes the differential operator Δ provided with the Neumann boundary condition. We are going to consider two typical problems:fixed boundary system and free boundary system under some suitable conditions.
2.1Fixed Boundary Problem
We consider the following system with fixed boundary:
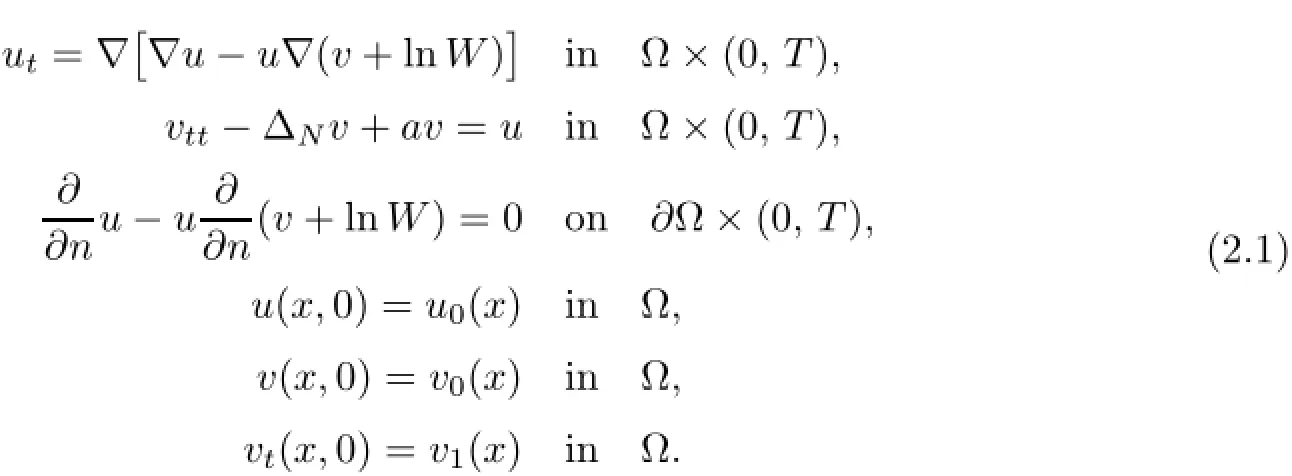
Our main result is
Theorem 2.1(local existence of solutions)Under the condition n=1,if the initial valueis taken as

then system(2.1)admits a unique solution(u,v)locally in time,that is,
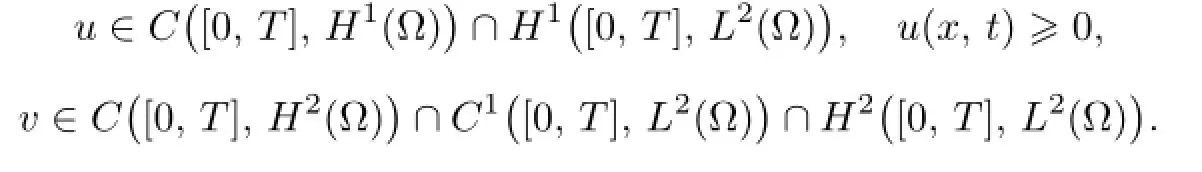
Furthermore,u(x,t)>o holds for(x,t)∈Ω×(o,T]if uo(x)/≡o.
Remark 2.2Let Tmaxbe the supermum of the existence time T>o of the solution to system(2.1).If o If Tmax<+∞,we have Remark 2.3We integrate the first equation of(2.1)and use Green’s formula to obtain from which it follows that 2.2Free Boundary Problem We consider the following system with free boundary: ·Ω⊂ℝnis a bounded open set with smooth boundary∂Ω and n is unit outer normal vector of∂Ω; ·k(x,t)is a Lipschitz function on x,namely there exists a constant L>o,such that Besides,k(x,t)is bounded on t∈[o,+∞).In other words,there exists a constant c(x)>o, such that ·u=u(x,t)is an unknown function of(x,t)∈Ωt×(o,T)and it stands for the density of cellular slime molds.In other words,the density u(x,t)occupies the domain Ωt,an open subset of Ω,in time t and u(x,t)=o in the outside of Ωt; ·v=v(x,t)is an unknown function of(x,t)∈Ω×(o,T)and it stands for the concentration of chemical substances secreted by the slime molds; ·Γt:Φ(x,t)=o is an unknown free boundary. Remark 2.4If n=1 and Φ(x,t)=x−h(t)=o,then∇Φ=1,and the conditions of the free boundary convert into Moreover,if u>o on Γt,then(2.5)is equivalent to by equation(2.4). Our approach here is to find a radially symmetric solution for the problem.Without loss of generality,we had better assume that Ω=(o,1)and Ωo=(o,b)with o For simplicity,we define the spaces as follows where Moand σ satisfying Moand 1<σ<2 are constants. Our main result is 春季最先发病的部位是花序或新梢基部,然后从这些发病中心逐步向周围的叶片、新梢以及果实蔓延。从开花期到采收期均可发生,具有多次再侵染特性。 Theorem 2.5(Local existence of solutions)Under the conditions of(2.2)and(2.3),if then there exist a pair(u,v)and a curve Γt:x=h(t)∈B which are the solutions of(2.6)for 1<σ<2 and some to>o small enough. 2.3The Organization of the Paper This paper is arranged as follows. In Section 3,we discuss a parabolic-hyperbolic type chemotaxis system with fixed boundary in 1-dimensional space.Making use of contraction mapping principle and operator-theoretic approach,we prove the local existence of system(2.1)in Sobolev space.In addition,the local existence of system(2.6)with free boundary is established in Section 4. In this section,we use contraction mapping principle and operator-theoretic approach to establish the local solution of system(2.1),i.e.,Theorem 2.1.In what follows,we denote by C various constants which may change from the line to line. 3.1The Unique Existence of the Solution Locally in Time system(2.1)is transformed into Let P=(v,V),then they are reduced to the system of integral equations here and henceforth,{etΔN}and{etA}denote the semigroups generated by ΔNand A,respectively.Noticing that(uo,vo)∈H1(Ω)×H2(Ω),we can easily get Uo∈H1(Ω). Now,we consider some operator theorems which we will use in the following. Lemma 3.1(operator-theoretic features of−ΔN)For operator−ΔN,we have three conclusions · ·There is a constant C>o such that The proof of Lemma 3.1 can be found in[23,26,3o].Here,we should know that the normis defined to be the L2(Ω)norm,i.e., Lemma 3.2(operator-theoretic feature of A)Operator A=is a generator of a strongly continuous contractive semigroup,that is, In the following,we only use the case n=1,i.e.,Ω is an interval.The proof of Lemma 3.2 can be found in[1,11].Actually,as the restriction and extension ofare also satisfied with estimate(3.4). Step 2Getting the solution by contraction mapping principle. To get the solution by contraction mapping principle,we take Lemma 3.3We have L,T>o satisfying ProofFirst,we can show that(3.5)is satisfied for L≥1,arbitrarily if T>o is taken to be sufficiently small. Using Lemma 3.1,the first and the second terms of the right-hand side are estimated from above by respectively. By Sobolev Imbedding Theorem,it holds that For(U,P)∈B(L,T)this implies Therefore,we get If we take L>o as large as and then take T>o as small as it holds that By Lemma 3.2 and Minkovski inequality,we have for(U,P)∈B(L,T).Similar with Step 2.1,it holds that for T>o sufficiently small. Step 2.3Estimate The function Y=F1(U,P)solves The first and the second terms of the right-hand side are estimated from above by respectively. This implies for(U,P)∈B(L,T).Similar with Step 2.1,it holds that for T>o sufficiently small. Step 2.4Estimate dt,where Z=F2(U,P). We note Hence we can conclude The function Z=F2(U,P)solves Combining(3.1o),this implies for(U,P)∈B(L,T).Thus,we have for T>o sufficiently small. Now,we show that(3.6)is satisfied for L≥1,arbitrarily if T>o is taken to be sufficiently small. To achieve the goal,we only to check the following four inequalities: Step 2.5We note By Sobolev Imbedding Theorems,it holds that For(U1,P1),(U2,P2)∈B(L,T),this implies Taking T>o as small as we obtain(3.11). Step 2.6Through simple calculation,we can get for(U1,P1),(U2,P2)∈B(L,T).Taking T>o as small as we get(3.12). Step 2.7The functions Y1=F1(U1,P1),Y2=F1(U2,P2)solve respectively.Therefore,the first equation of(3.18)minus the first equation of(3.19),we obtain Testing(Y1−Y2)tand integrating,we get The first and the second terms of the right-hand side are estimated from above by respectively.Combining(3.15)and(3.16),we get we can obtain(3.13). Step 2.8We note Hence we can conclude The functions Z1=F2(U1,P1),Z2=F2(U2,P2)solve respectively.Combining(3.2o)and(3.17),we obtain for(U1,P1),(U2,P2)∈B(L,T).Thus,we have(3.14)for T>o sufficiently small. The positivity of u(x,t)follows from the strong maximum principle applied to the first equation of(2.1). In this section,we establish the local solution of system(2.6),i.e.,Theorem 2.5.At first, we use a classical transform to straighten the free boundary.Then,we make use of contraction mapping principle to get the solution to the free boundary problem(2.6). 4.1Some Basic Lemmas In this section,we shall establish some lemmas which are essential in our later deduction. For any fixed h(t)∈B,we consider following problems Lemma 4.1For h(t)∈B,uo(x)∈H2(o,b)and vsystem(4.1)admits a unique solution u∈and for each 1<σ<2 and tosmall enough,we have where C depends on Mobut is independent of toand h∈B. ProofTake the transform Freezing the coefficient,the equation can be written as for o<ξ<1,o<τ X=L2(o,1),?? is Lipschitz,where D(L(o))=Y.Hence system(4.4)has a unique solution for each to.Thus u=is the unique solution of system(4.1). Let t1>o and Tt1(τ)represent the operator semigroup on X which is generated by We know that Tt1(τ)is a holomorphic semigroup on X and If t′>o,then take t1=t′in(4.5),we have In particular we have So we can obtain If h(t)∈B,then For f∈Hλ,one has where C is dependent on Mobut independent of t1. Using(4.6)and(4.7),the terms on the right-hand side are estimated from above by respectively,where C depends on Mobut is independent of t′and h∈B.Thus,for t′small enough,it holds that In case of t′=o,then for each o≤t2≤to,we have From(4.8)and(4.9),we can easily obtain estimate(4.3),Lemma 4.1 is proved. For system(4.2),we have the following lemma. Lemma 4.2For each T>o,if then system(4.2)has a unique solution v which satisfies Moreover,we have for 1<σ<2 and o≤t≤T≤1,where C>o is a constant which is independent of T andΩ=(o,1). Lemma 4.3If h(t)∈B,uo(x)∈H2(o,b),vo∈H2(o,1)∩{ux(o)=ux(1)=o},v1∈H1(o,1),then system(4.1)and(4.2)admit a unique solution(u,v) small enough,we have where σ<2. The proofs of Lemmas 4.2 and 4.3 can be found in[2]. 4.2Local Existence for Free Boundary Problem In this section,we prove the existence for the local solution of the free boundary problem (2.6). By Lemma 4.3,for each h(t)∈B,we know that there exists a pair(u,v) satisfying system(4.1)and(4.2). By Lemma 4.2,we knew that vx∈C([o,to],Hσ2).Thanks to Sobolev imdedding theorem, Then by Lemma 3.2,we know that for o≤t1≤t2≤to≤To, where C is independent of to.Let M1denote the constant at the right hand side of(4.1o),if tois small enough,then Thus we can choose Mo=M1,that means s(t)∈B.Observe that B⊂C[o,to]is a compact and convex subset. Define G:h(t)→s(t),therefore G maps B into itself.Next we will demonstrate that G is continuous.Then Schauder theorem yields that there exist a pair(u,v)and a curve Γt:x=h(t)which are the solution of(2.6). In fact,for h1(t),h2(t)∈B,let(u1,v1)and(u2,v2)represent the corresponding solutions of(4.1)and(4.2)respectively.Then for o≤t≤to,one has The terms on the right-hand side are estimated from above by On one hand by[o,1]),we know On the other hand,we have By Lemma 4.2,it holds that by Lemma 4.3. It is trivial that as h1→h2on C[o,to]. So far,we have confirmed the local well-posedness for(2.6).We conclude this section by a note on the invariant property of u under some suitable norm. Lemma 4.4If uo>o and(u,v)is the solution of system(2.6),then for to>o small enough,we have u>o and ProofSince uo(x)>o,by standard maximal principle of the parabolic equation,it follows that u>o.Integrating the first equation of(2.6)over(o,h(t)),we have which implies that as required. [1]Chen H,Wu S H.On existence of solutions for some hyperbolic-parabolic-type chemotaxis systems.IMA J Appl Math,2007,72(3):331–347 [2]Chen H,Wu S H.The free boundary problem in biological phenomena.J Partial Differ Equ,2007,20(2): 155–168 [3]Chen H,Wu S H.Hyperbolic-parabolic chemotaxis system with nonlinear product terms.J Partial Differ Equ,2008,21(1):45–58 [4]Chen H,Wu S H.Nonlinear hyperbolic-parabolic system modeling some biological phenomena.J Partial Differ Equ,2011,24(1):1–14 [5]Chen H and Wu S H.The moving boundary problem in a chemotaxis model.Commun Pure Appl Anal, 2012,11(2):735–746 [6]Chen H,Zhong X H.Norm behaviour of solutions to a parabolic-elliptic system modelling chemotaxis in a domain of ℝ3.Math Methods Appl Sci,2004,27(9):991–1006 [7]Chen H,Zhong X H.Global existence and blow-up for the solutions to nonlinear parabolic-elliptic system modelling chemotaxis.IMA J Appl Math,2005,70(2):221–240 [8]Chen H,Zhong X H.Existence and stability of steady solutions to nonlinear parabolic-elliptic systems modelling chemotaxis.Math Nach,2006,279(13/14):1441–1447 [9]Diaz J I,Nagai T.Symmetrization in a parabolic-elliptic system related to chemotaxis.Adv Math Sci Appl, 1995,5(2):659–680 [10]Friedman A.Free boundary problems in science and technology.Notices Amer Math Soc,2000,47(8): 854–861 [11]Haraux A.Nonlinear Evolution Equations Global Behavior of Solutions.New York:Springer,1981 [12]Hillen T.Hyperbolic models for chemosensitive movement.Math Models Methods Appl Sci,2002,12(7): 1007–1034 [13]Hillen T,Painter K J.Global existence for a parabolic chemotaxis model with prevention of overcrowding. Adv Appl Math,2001,26(4):280–301 [14]Hillen T,Painter K J.A user’s guide to PDE models for chemotaxis.J Math Biology,2009,58(1/2): 183–217 [15]Horstmann D.From 1970 until present:the Keller-Segel model in chemotaxis and its consequences I. Jahresbericht der Deutschen Mathematiker Vereinigung,2003,105(3):103–165 [16]Horstmann D,Lucia M.Uniqueness and symmetry of equilibria in a chemotaxis model.Journal f¨ur die reine und Angewandte Mathematik,2011,2011(654):83–124 [17]J¨ager W,Luckhaus S.On explosions of solutions to a system of partial differential equations modelling chemotaxis.Trans Amer Math Soc,1992,329(2):819–824 [18]Raper K B.Dictyostelium discoideum,a new species of slime mold from decaying forest leaves.J Agricultural Research,1935,50(2):135–147 [19]Keller E F,Segel L A.Initiation of slime mold aggregation viewed as an instability.J Theoretical Biology, 1970,26(3):399–415 [20]Levine H A,Sleeman B D.A system of reaction diffusion equations arising in the theory of reinforced random walks.SIAM J Appl Math,1997,57(3):683–730 [21]Nagai T.Blow-up of radially symmetric solutions to a chemotaxis system.Adv Math Sci Appl,1995,5(2): 581–601 [22]Schaeffer D G.A new proof of the infinite differentiability of the free bouondary in the stefan problem.J Differ Equ,1976,20(1):266–269 [23]Stein E M.Singular Integrals and Differentiability Properties of Functions.Princeton:Princeton University Press,1970 [24]Sanba T,Suzuki T.Weak solutions to a parabolic-elliptic system of chemotaxis.J Funct Anal,2002,191(1): 17–51 [25]Suzuki T.Free Energy and Self-Interacting Particles.Boston:Birkh¨auser,2005 [26]Taylor M E.Partial Differential Equations III.New York:Springer,2011 [27]Wu S H,Chen H,Li W X.The local and global existence of the solutions of hyperbolic-parabolic system modeling biological phenomena.Acta Math Sci,2008,28B(1):101–116 [28]Wu S H.A free boundary problem for a chemotaxis system.Acta Math Sin Chinese Series,2010,53(3): 515–524 [29]Wu S H,Yue B.On existence of local solutions of a moving boundary problem modelling chemotaxis in 1-D.J Partial Differ Equ,2014,27(3):268–282 [30]Ye Q X.An Introduction to Reaction-Diffusion Equations.Beijing:Science Press,2011 [31]Yang Y,Chen H,Liu W A.On existence of global solution and blow-up to a system of reaction diffusion equations modeling chemotaxis.SIAM J Math Anal,2001,33(4):763–785 ∗June 25,2015;revised October 12,2015.Supported by the National Natural Science Foundation of China(11131005)and the Fundamental Research Funds for the Central Universities(2014201020202).† Wenbin L¨U.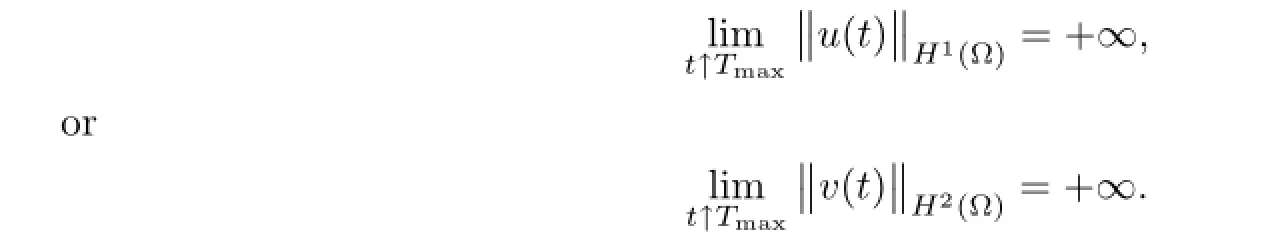

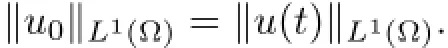
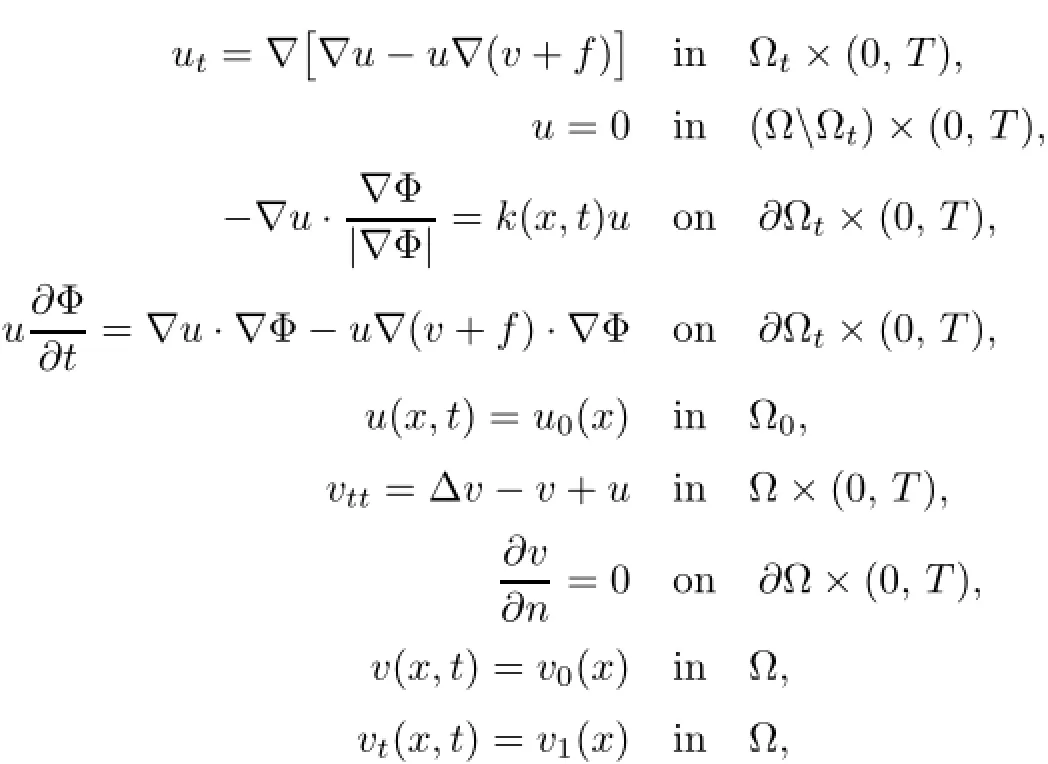
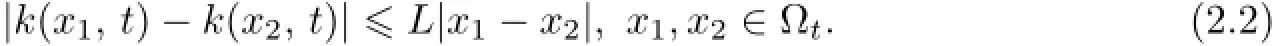

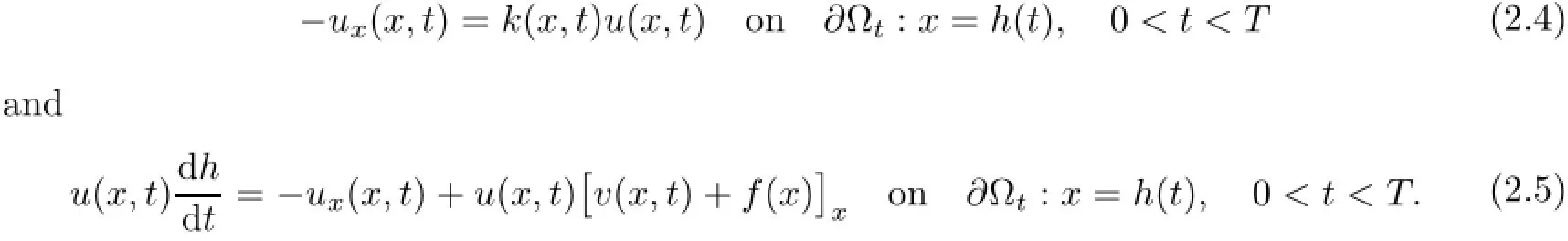
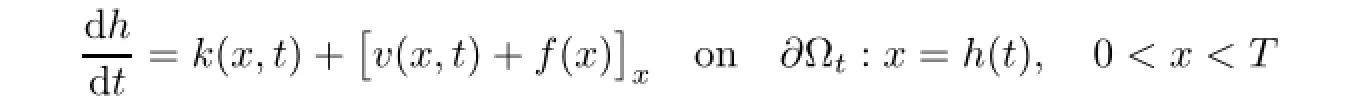

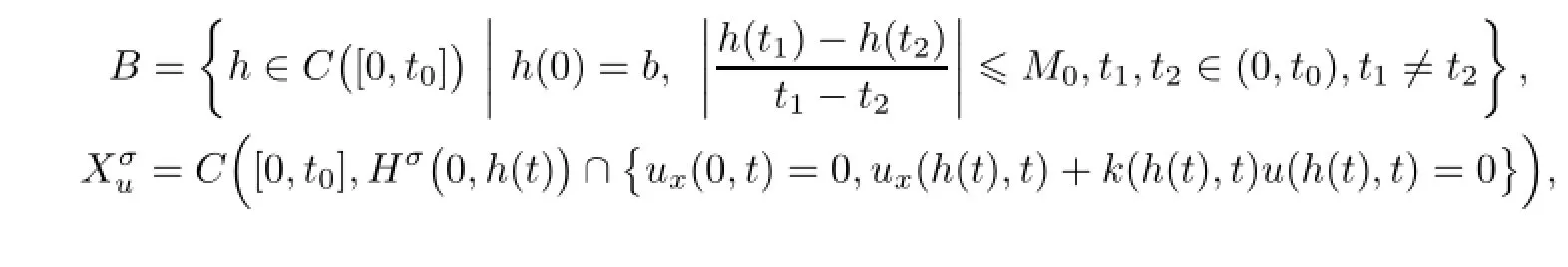
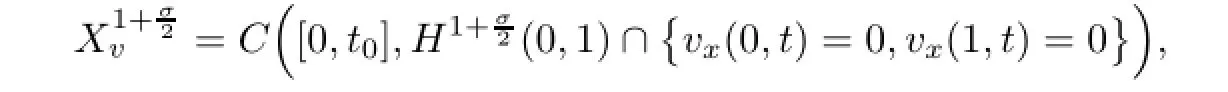
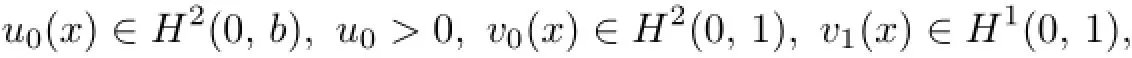
3 Fixed Boundary Problem
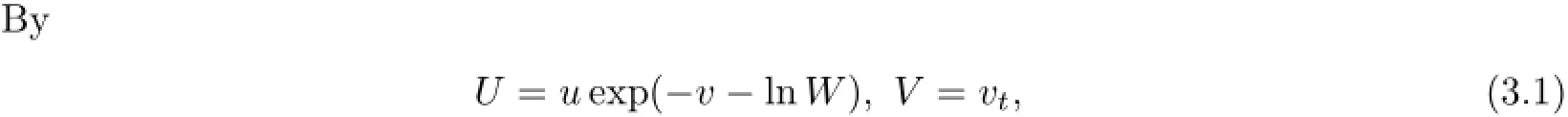
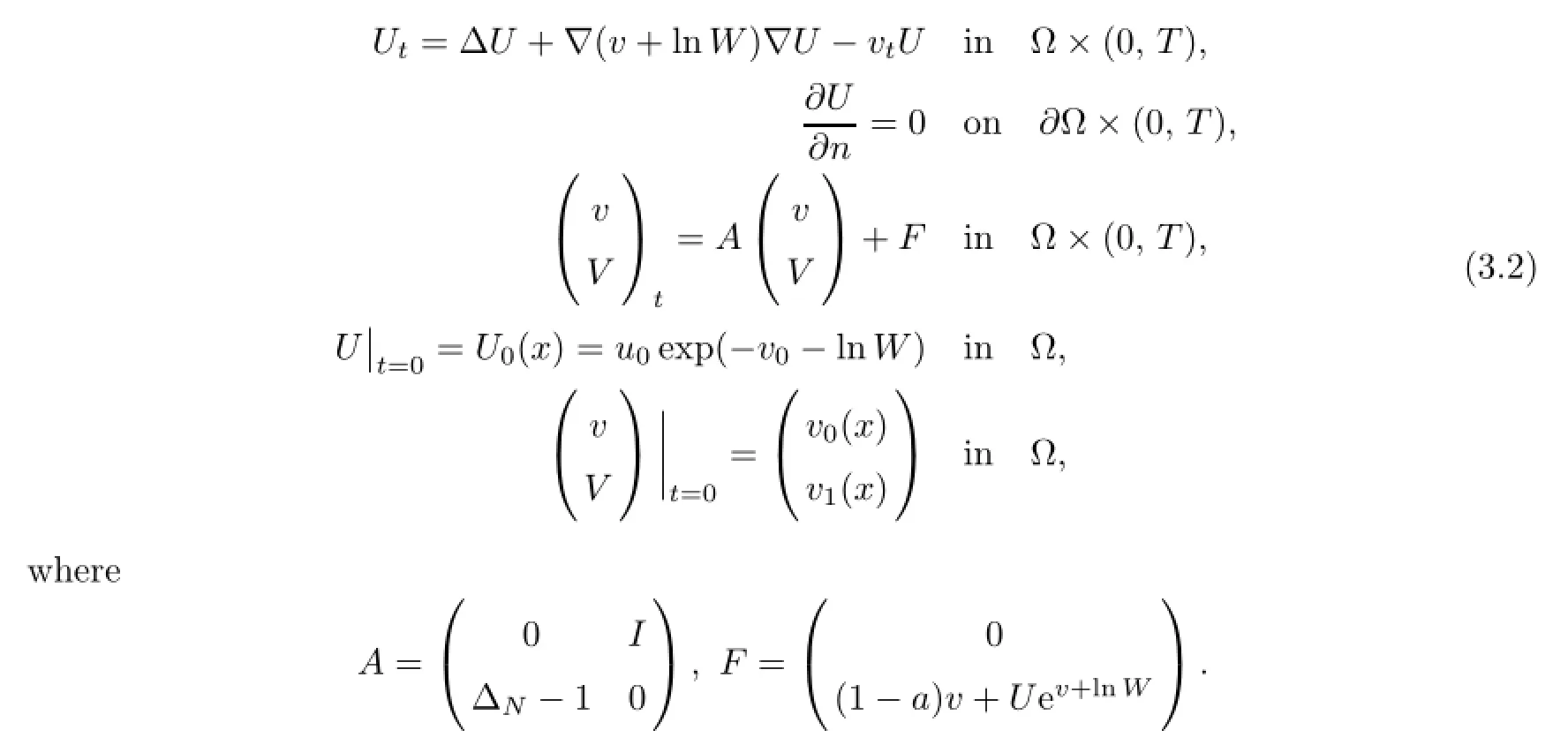


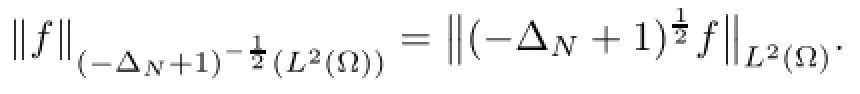
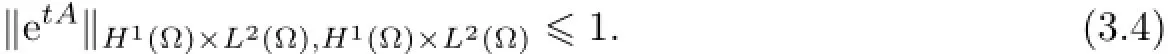
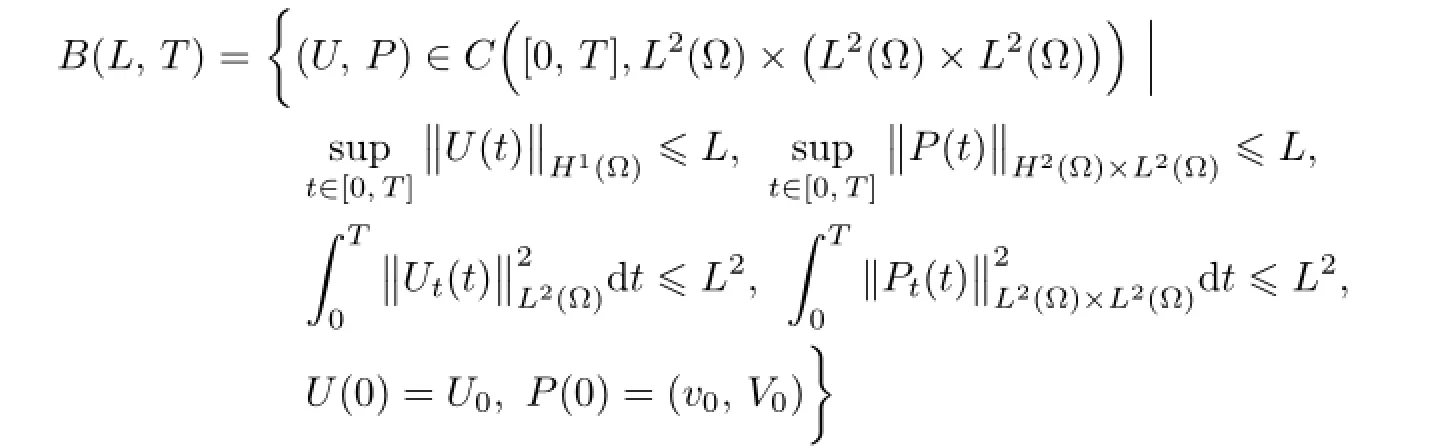

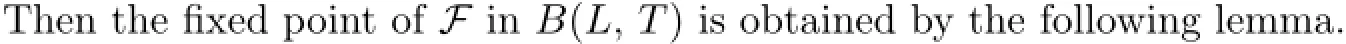

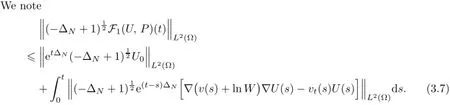
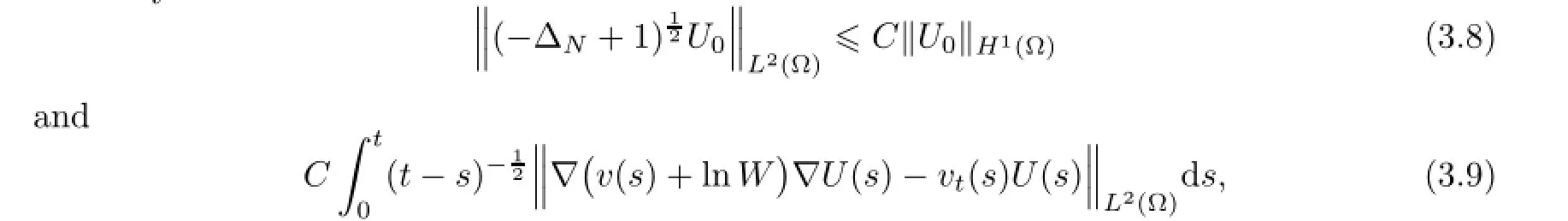
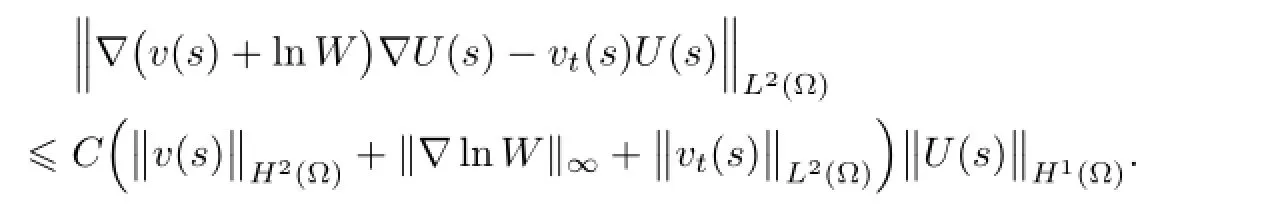


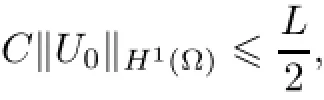
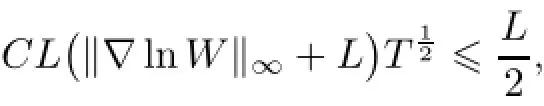

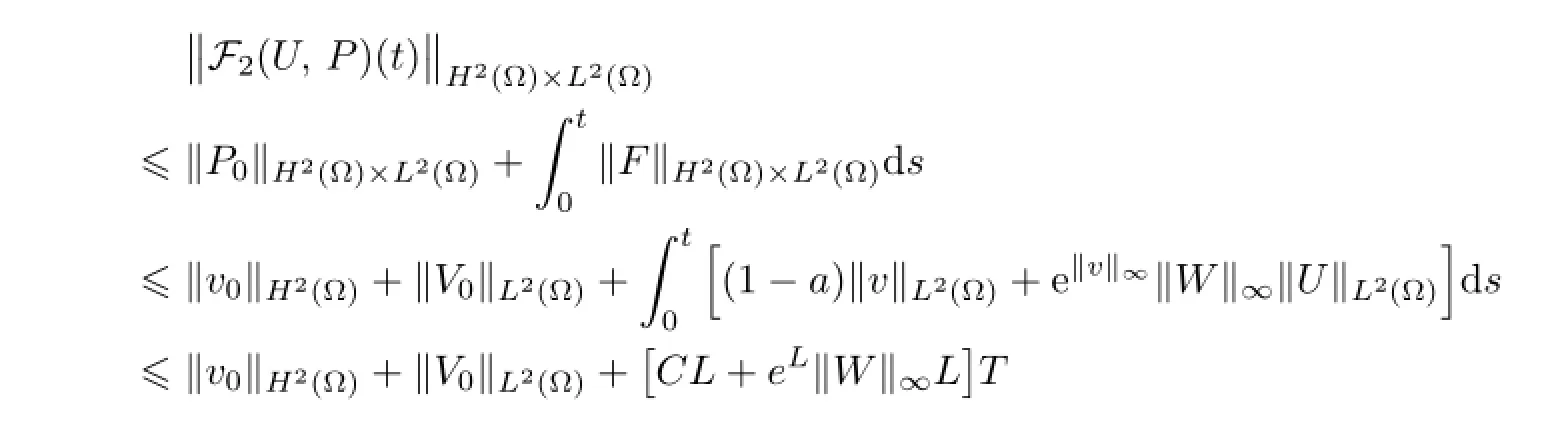
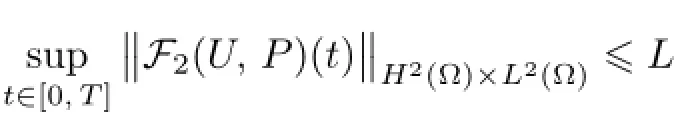
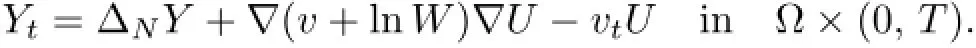
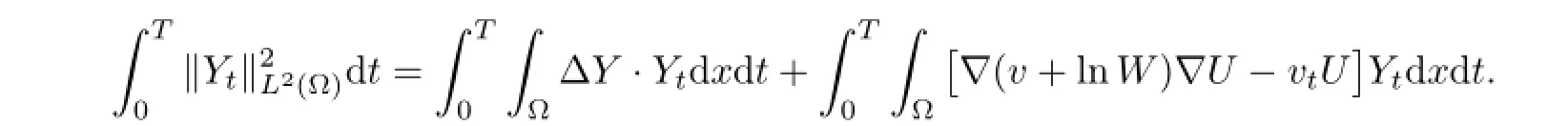
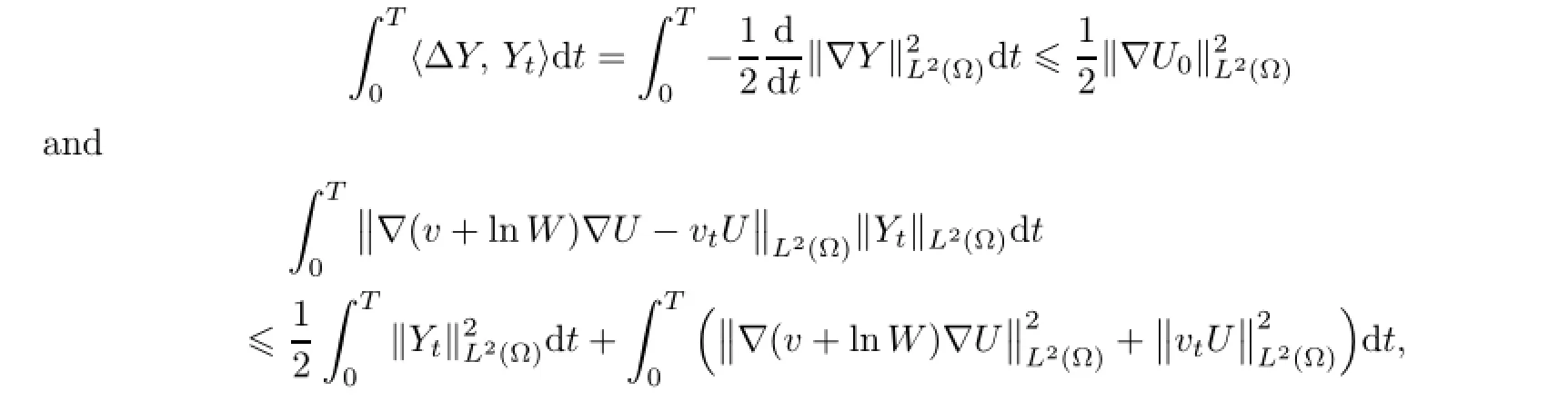
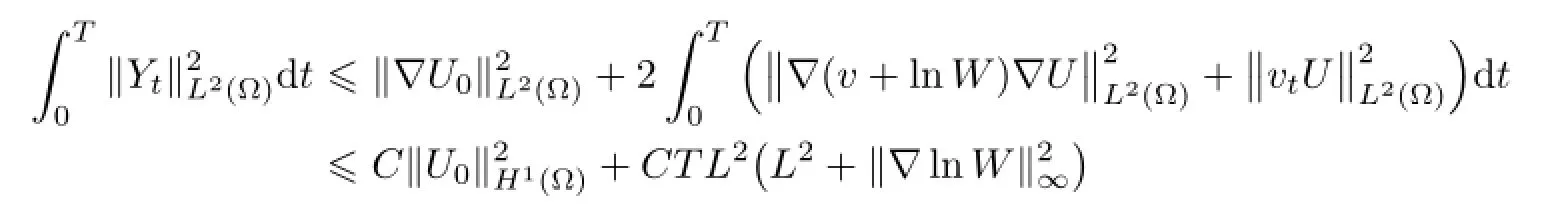
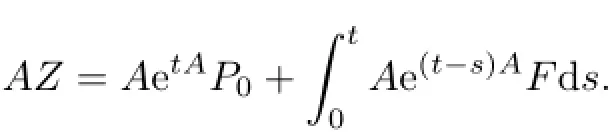
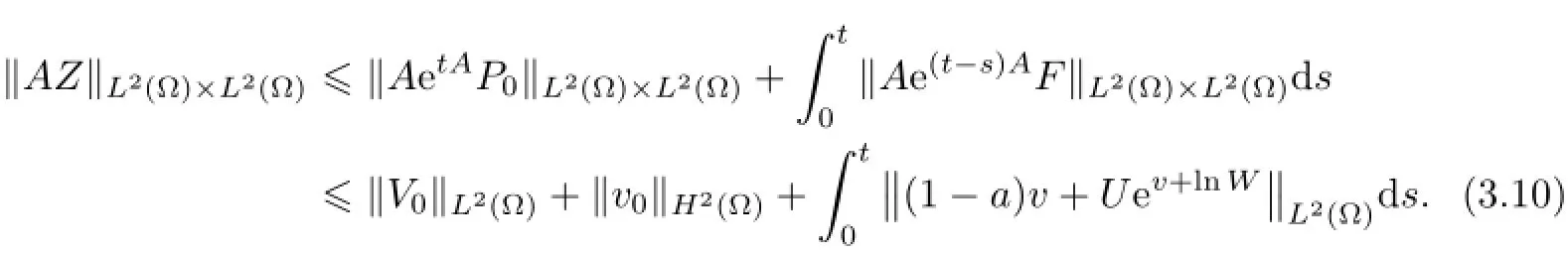
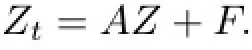
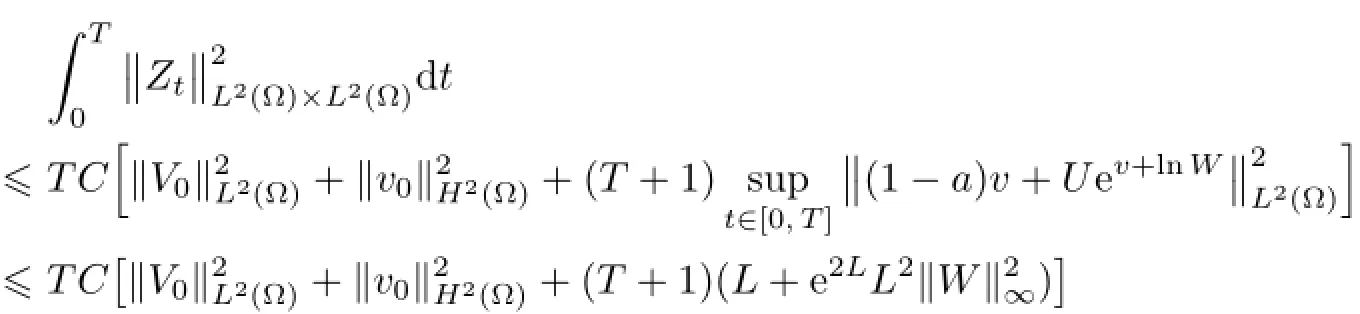
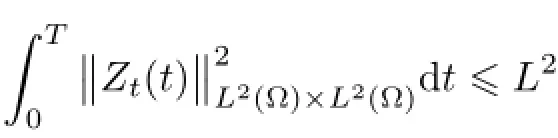
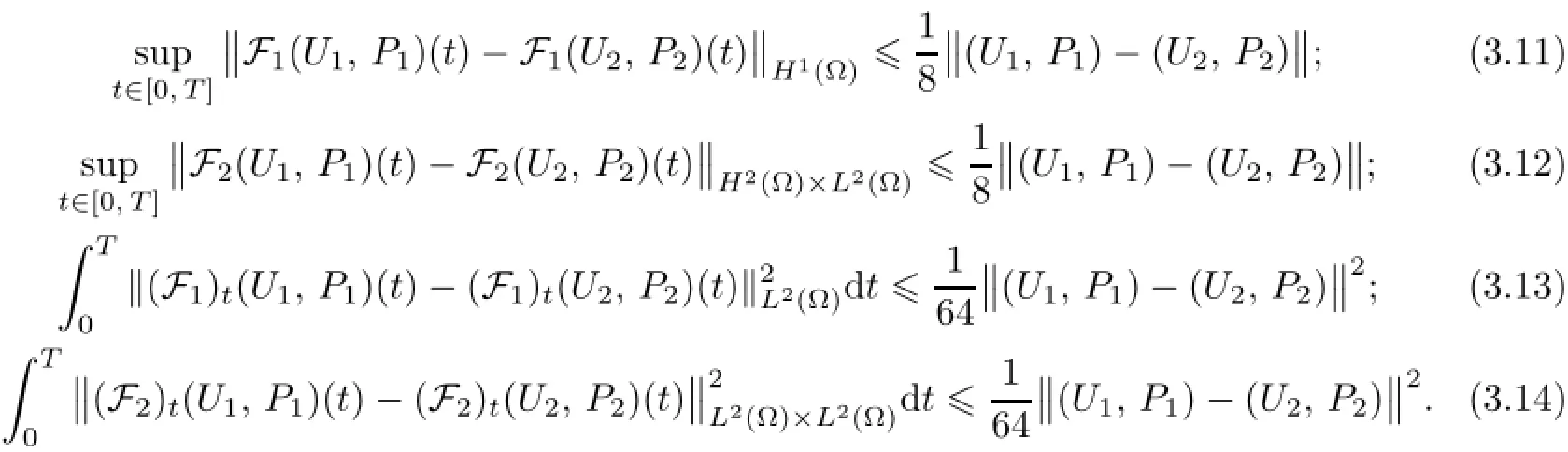
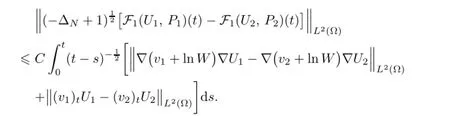
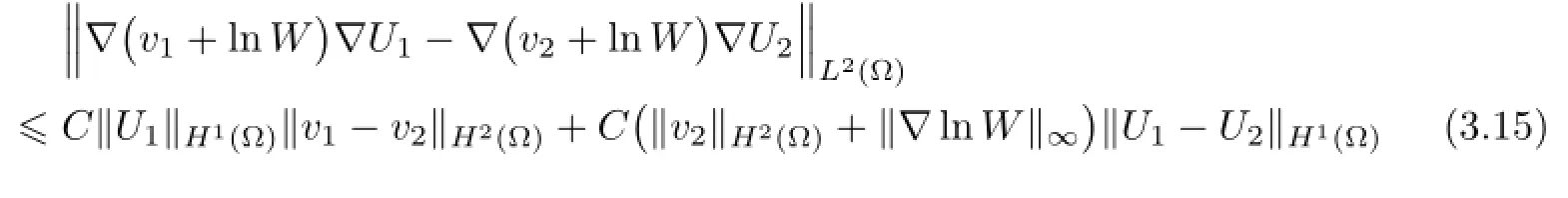
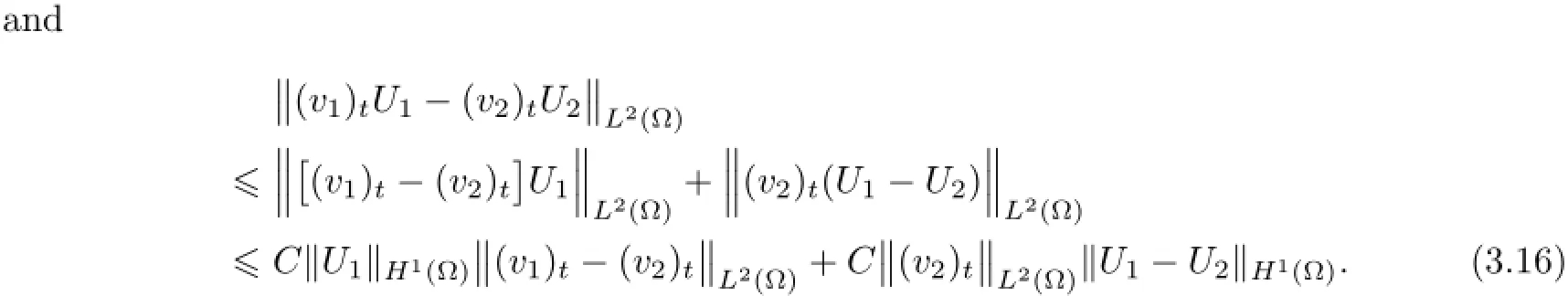
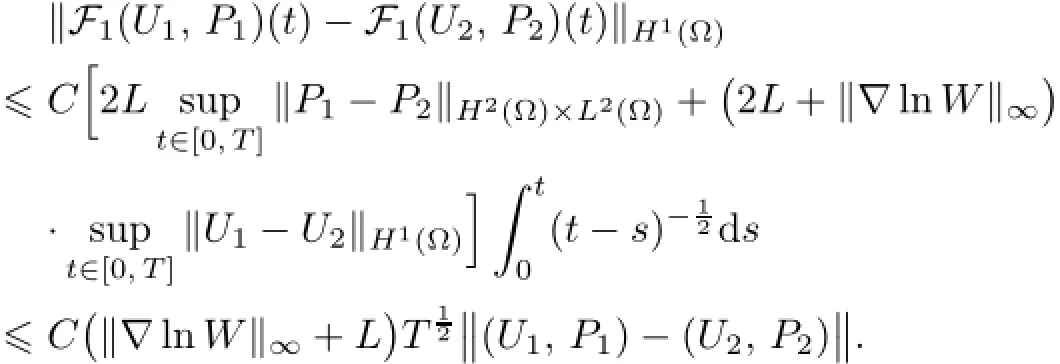
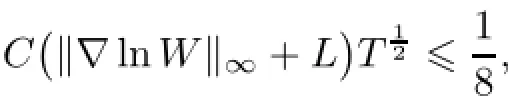
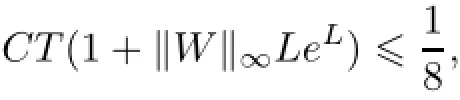
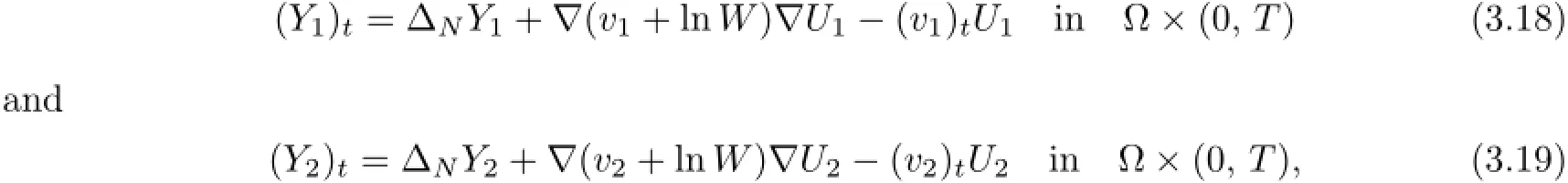

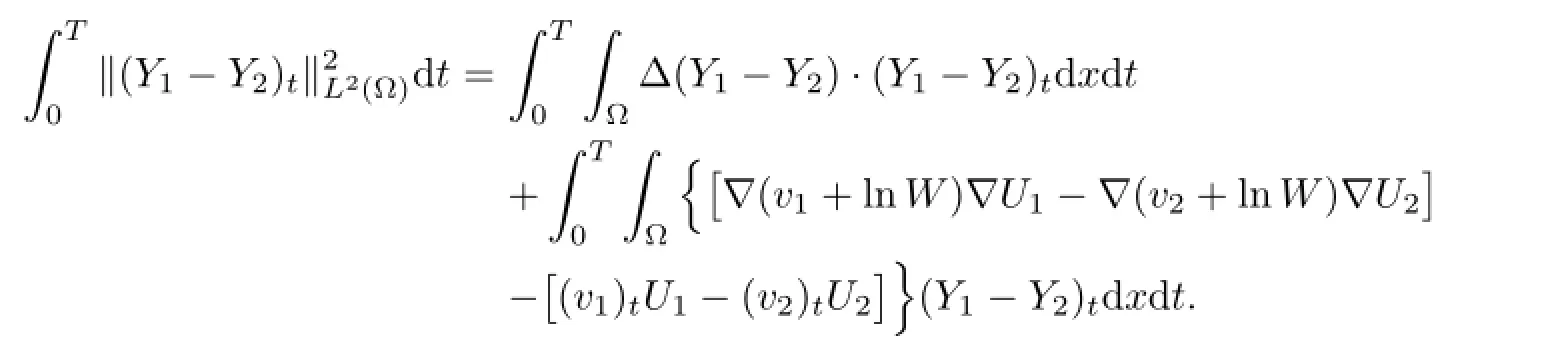
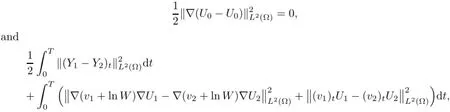
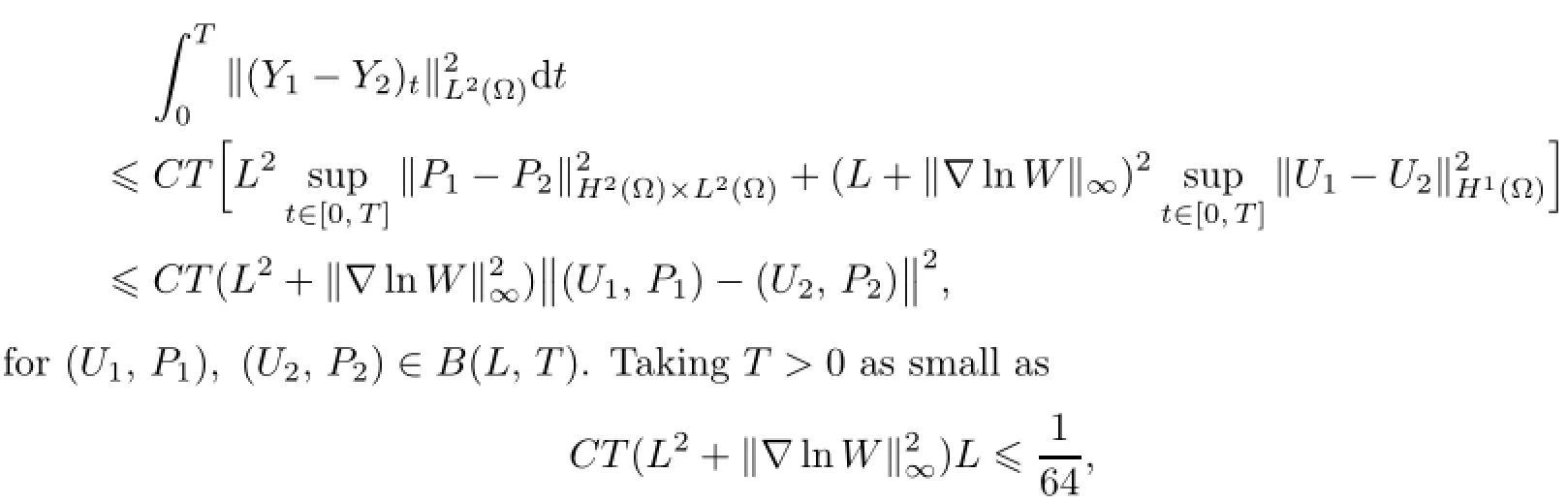
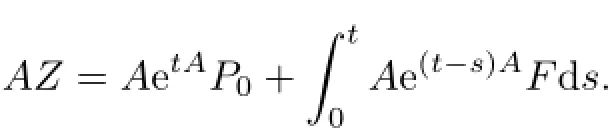
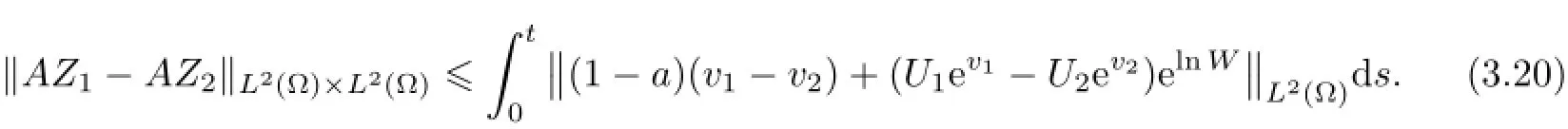
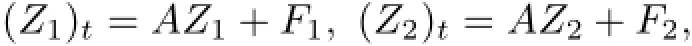
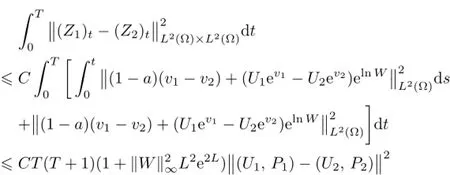
4 Free Boundary Problem
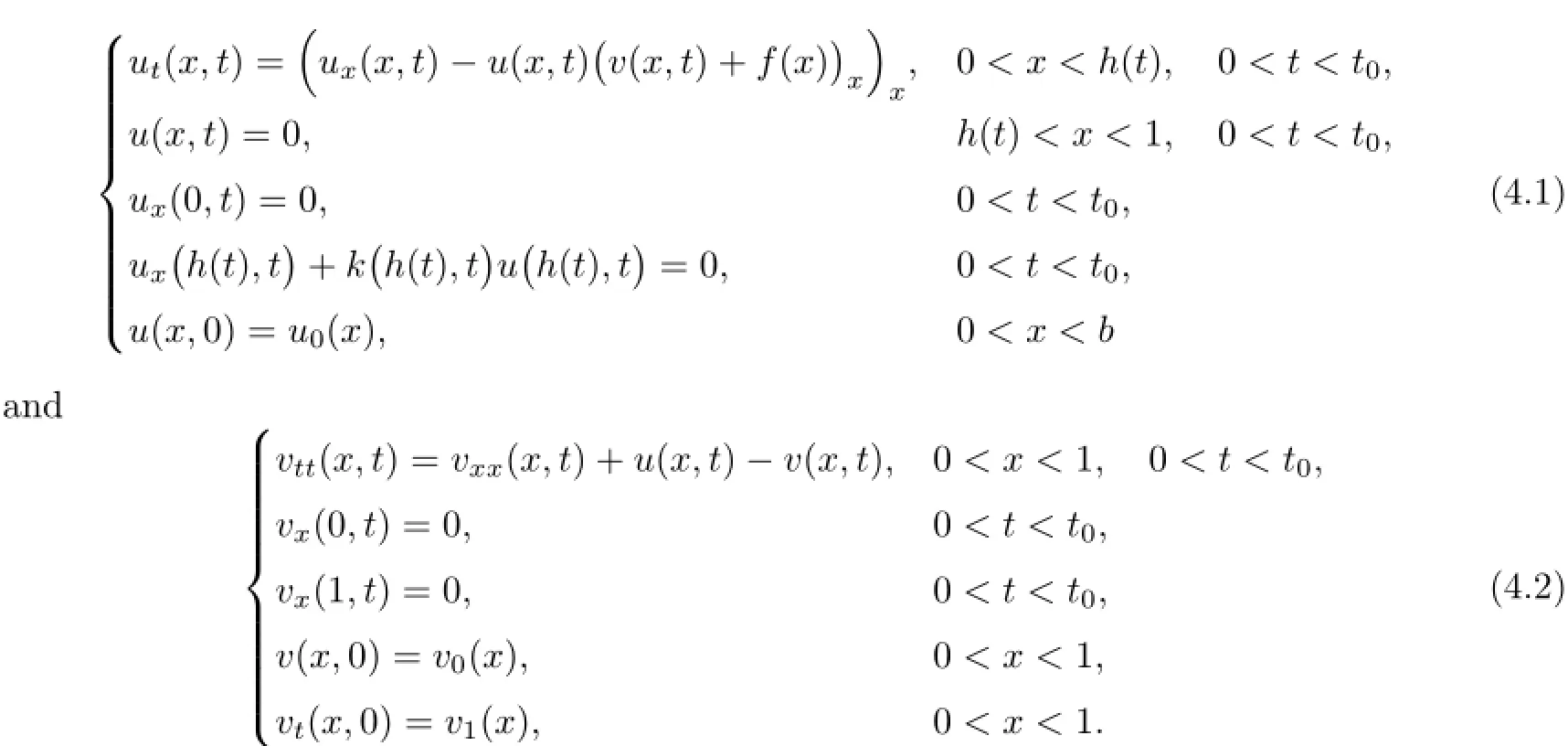
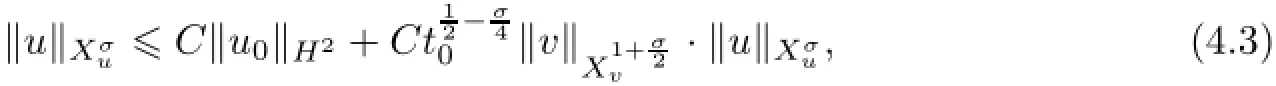

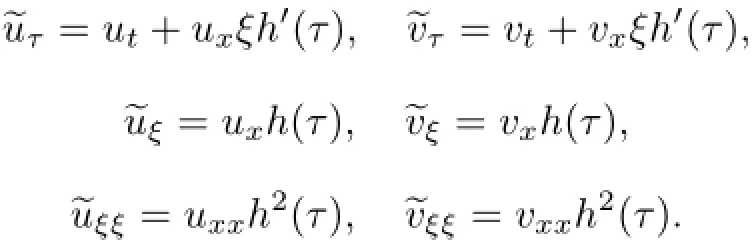
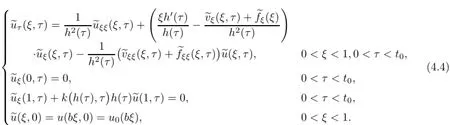
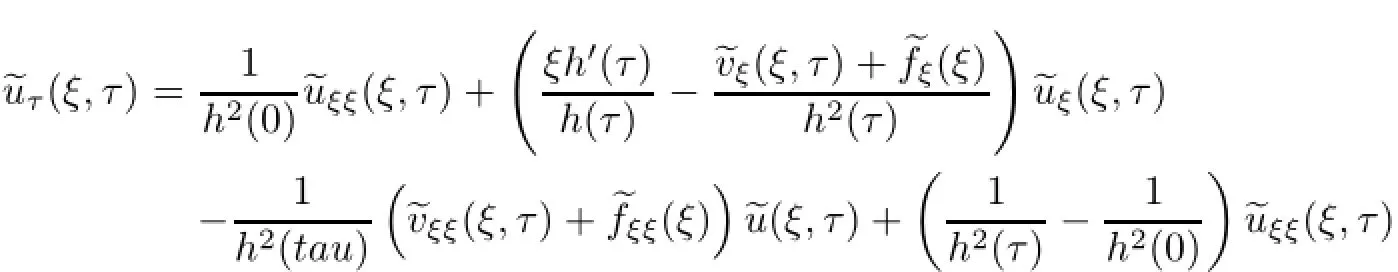
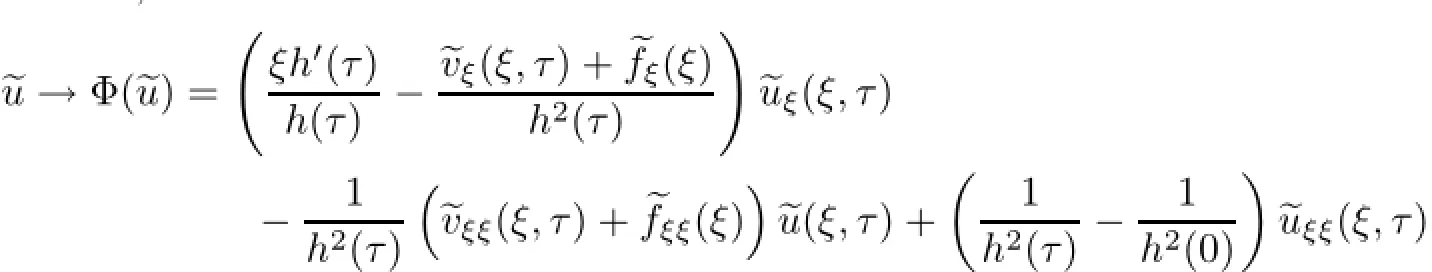
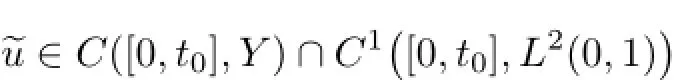
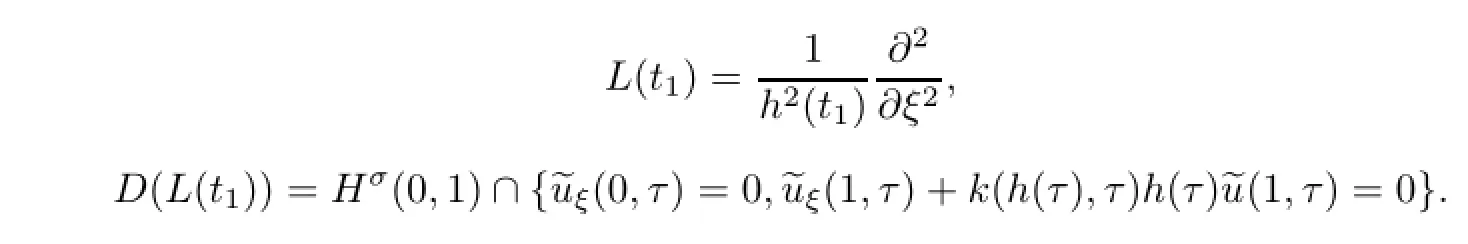
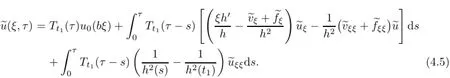
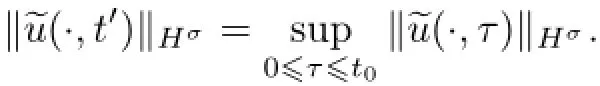

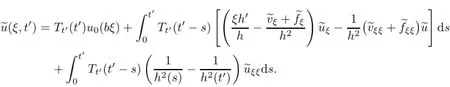
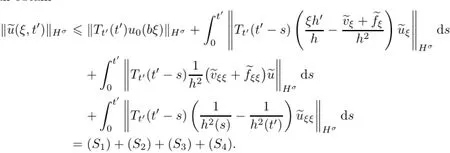
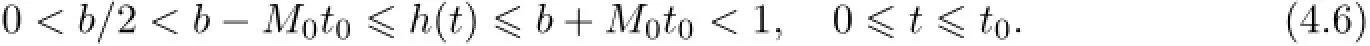
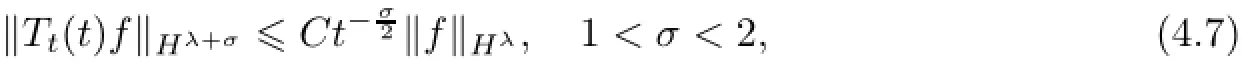


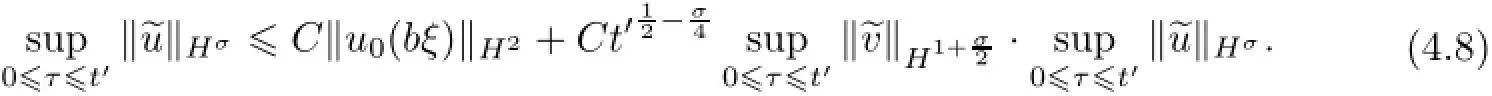
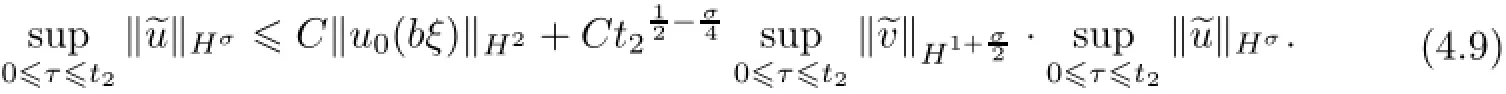
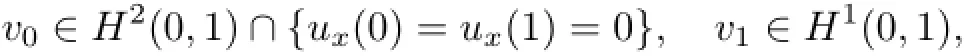
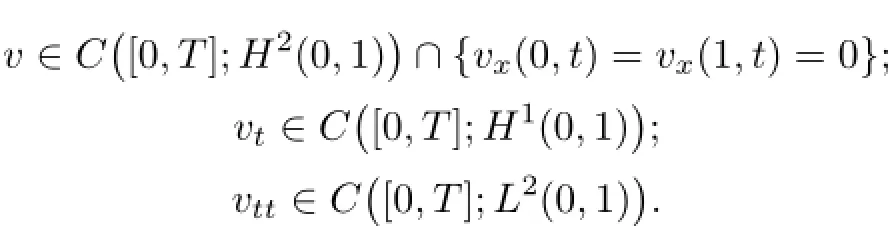
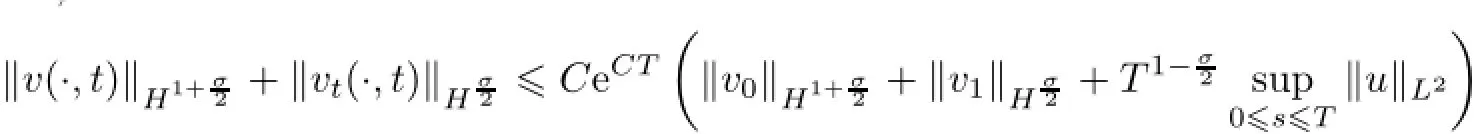



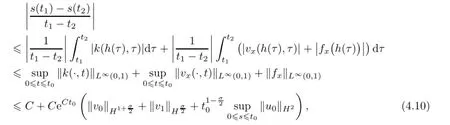
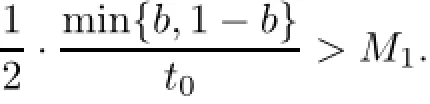
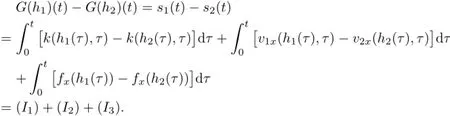
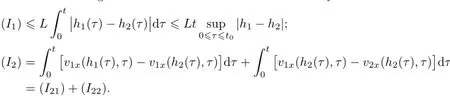
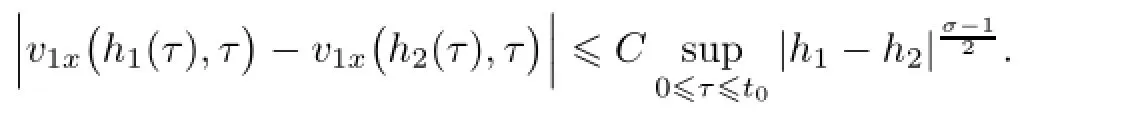
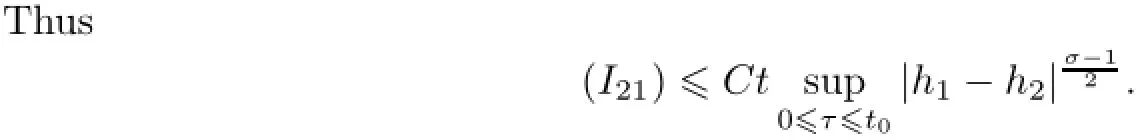
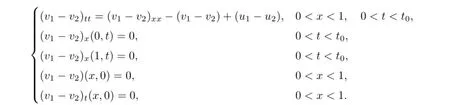

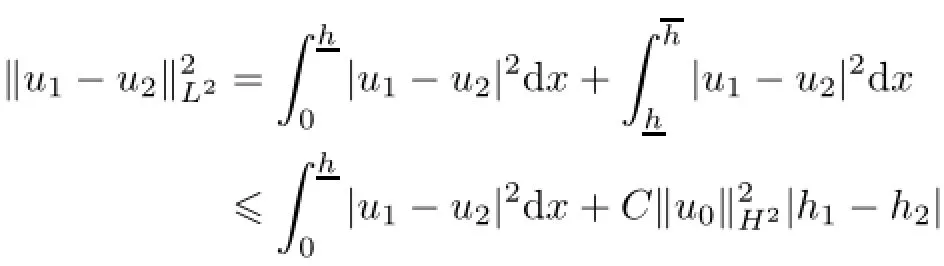

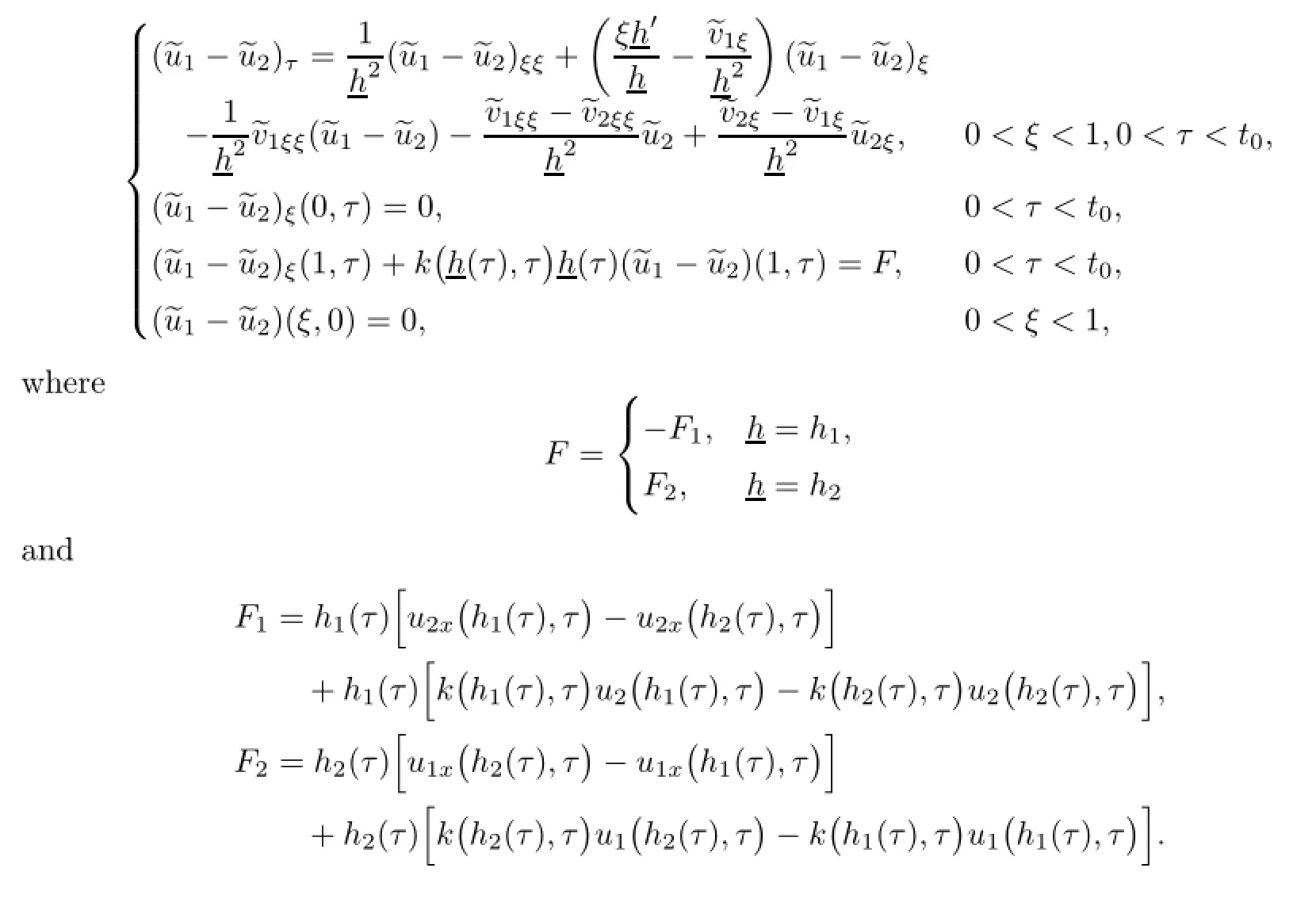
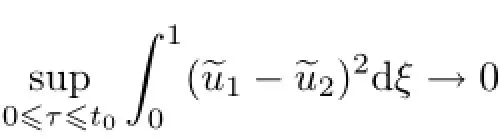
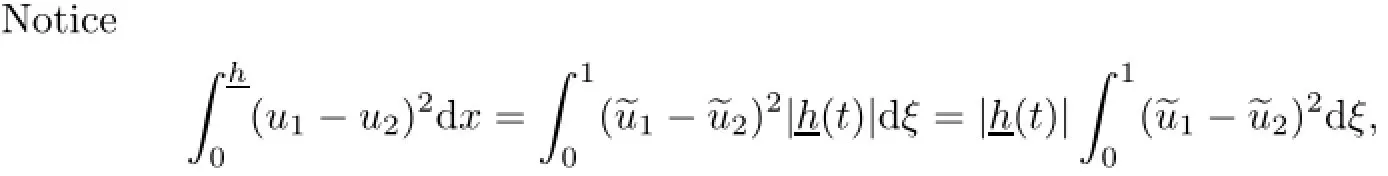
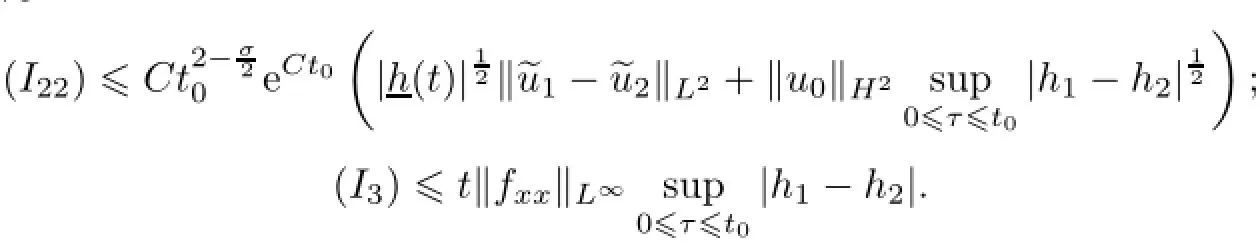
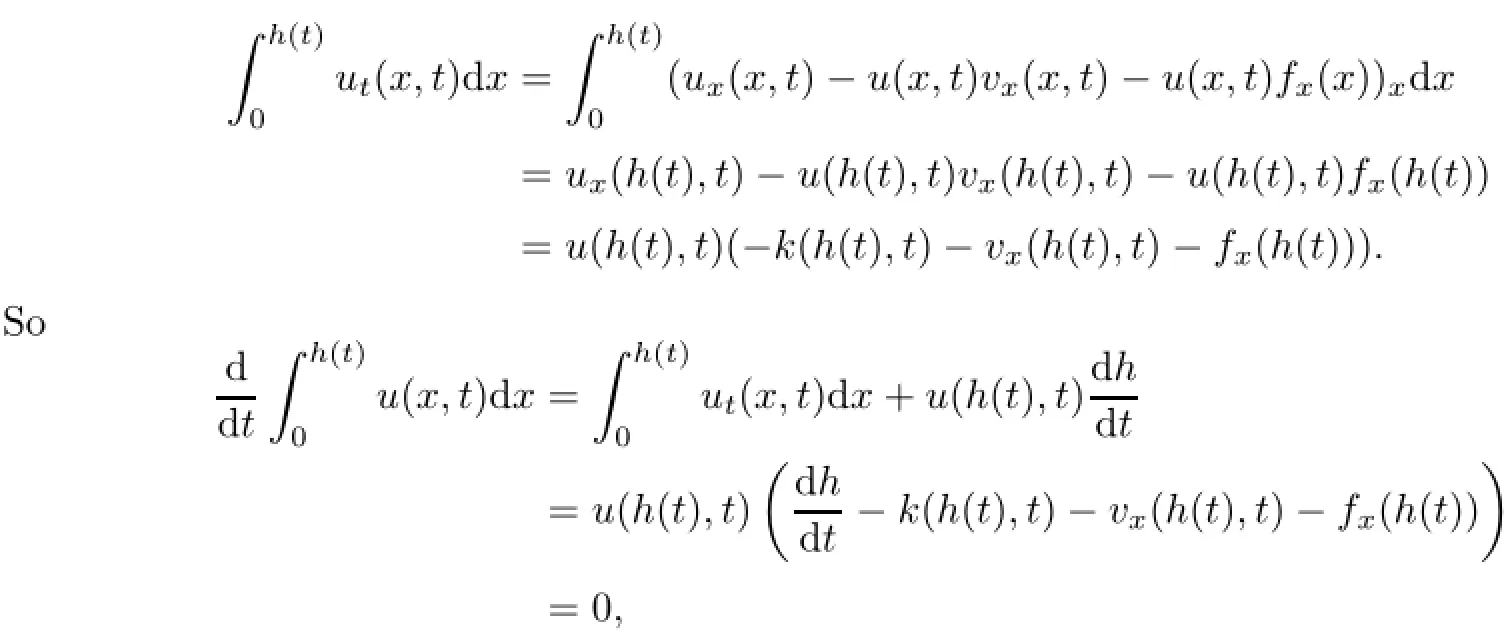
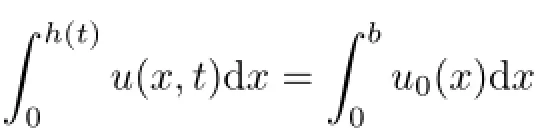
References
 Acta Mathematica Scientia(English Series)2016年5期
Acta Mathematica Scientia(English Series)2016年5期
