自然解法“无果”，另辟蹊径“有门”

☉江苏南京金陵中学河西分校　李玉荣

自然解法“无果”，另辟蹊径“有门”

☉江苏南京金陵中学河西分校李玉荣

一般而言，解题时最容易想到的解法当属自然解法，数学难题的自然解法通常不够简洁，有时甚至根本无法完成.改进自然解法或另辟蹊径，促使从自然解法走向完美解法是教师解题教学的职责和理想目标，路难走，但必须前行.

题目如图1，在梯形ABED中，∠D=∠E=90°，△ABC是等边三角形，且点C在DE上，如果AD=7，BE= 11，求△ABC的面积.（第24届希望杯初二）

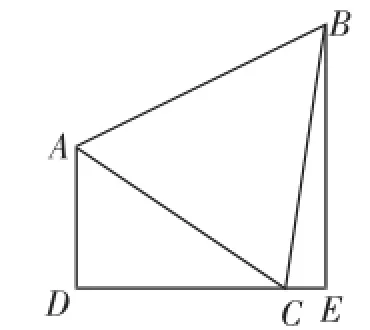
图1

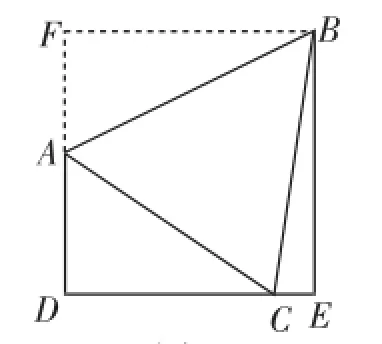
图2

解法1：如图2，作BF⊥DA交DA的延长线于点F，得矩形DEBF.

所以AF=BE-AD=4.设DC=x，CE=y，则BF=x+y.

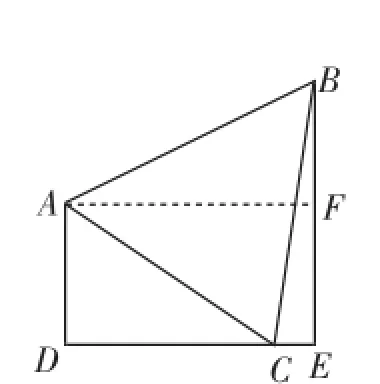
图3

这是二元二次方程组，初中生有能力求解吗？

解法2：如图3，作AF⊥BE交BE于点F，得矩形DEFA，所以BF=BEAD=4.设AB=AC=BC=x，则DC=

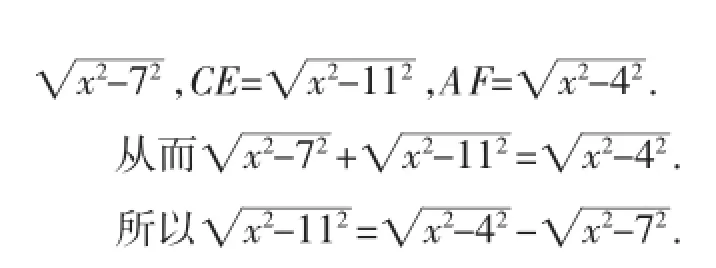
这是无理方程，初中生有能力求解吗？

点评：这两种解法是命题者提供的，从解题过程看，上述两种解法的难点显然是所列方程（组）超越了学生的能力范畴，难以求解，致使考生大多无法最终求出结果.可见解法虽很自然，但却并不完美.作为教师可以继续求解.

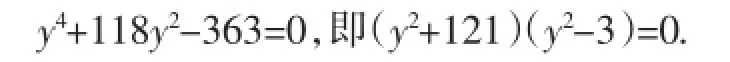
解得y2=3，从而BC2=BE2+CE2=121+3=124.

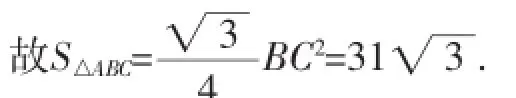
再两边平方、整理得：x4-124x2=0，解得x2=124.

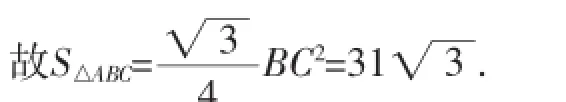
教师的求解固然可行，但改进解法让学生能够理解、接受势在必行.怎样改进这个自然解法呢？注意到△ABC是等边三角形，其特殊的角及线段相等可以使人联想到辅助圆，构造出特殊的直角三角形，避开自然解法中的方程组，得到以下完美解法.

图4

另解1：如图4，作BF⊥DA交DA的延长线于点F，则AF=BE-AD=4；

延长AD至点G，使得DG=AD= 7，则CG=CA=CB，故点G、A、B在以C为圆心，CA为半径的⊙C上.

【评注】此解法恰当地构造辅助圆，根据“一条弧所对的圆周角等于它所对的圆心角的一半”得到一个含30°角的直角三角形，巧妙地求出了BF，过程十分简洁，令人拍案叫绝.

另解2：如图5，作AG⊥BE于点

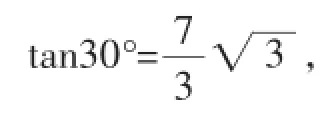
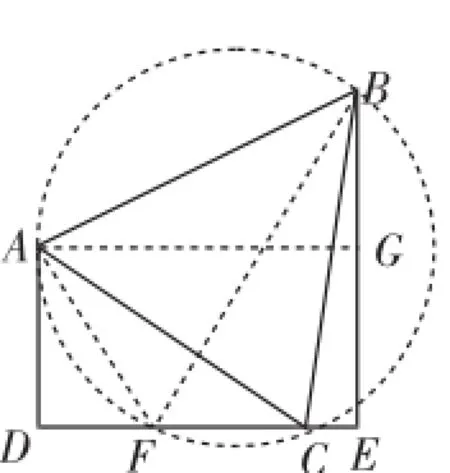
图5

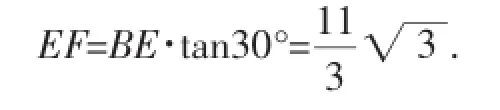
在Rt△AGB中，根据勾股定理得：

AB2=AG2+BG2=124.

【评注】此解法恰当地构造辅助圆，得到两个含30°角的直角三角形，巧妙地将AG转化为“AG=DE=DF+EF”求解，过程十分简洁，数学之精跃然纸上.

在解题教学中，本着自然生成的原则，寻求自然解法无可厚非，但因循守旧、故步自封也会一无所获.当用自然解法受挫时，教师就必须想方设法引导学生改进自然解法，或另辟蹊径寻求其他解法，从而起到化隐为显、化难为易的解题效果，实现解题从自然到完美的蜕变和升华.这正如人类的生存一样：尊重自然、敬畏自然，但要生活得更美好，必须适度改造自然、美化自然.Z