寻求不同切入点，提升学生思维品质——一道中考压轴题解析有感

☉天津市静海区沿庄镇中学　刘家良

寻求不同切入点，提升学生思维品质——一道中考压轴题解析有感

☉天津市静海区沿庄镇中学刘家良

（Ⅰ）如图1，当点A′与顶点B重合时，求点M的坐标；

（Ⅱ）如图2，当点A′落在第二象限时，A′M与OB相交于点C，试用含m的式子表示S；

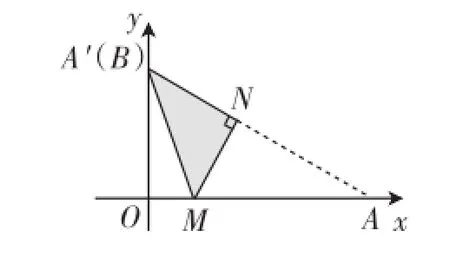
图1

图2

说明：2015年天津市中考数学试卷共25道题，由易到难的比为7:2:1.此题为第24题，第（Ⅰ）问属“7”的范畴，第（Ⅱ）问应在“2”内，第（Ⅲ）问应在“1”内，是全卷中的压轴题之一.

一、试题分析

这是一道以轴对称变换为“背景”，以轴对称的性质、勾股定理、三角函数、面积运算为考点，以转化、建模、分类、归纳为思想的中考试题.其中第（Ⅰ）问根据轴对称的性质，寻找到等边或等角，借助勾股定理列出方程或通过三角函数式变形的途径求值.此问起点低，侧重基础知识的考查；第（Ⅱ）问求重叠图形的面积.因为四边形MNBC是一个不规则的四边形，无法直接求得面积，所以求面积时，可结合与其相关图形之间的联系将其转化为若干个可求三角形面积的和、差运算，或连接对角线BN将其化为两个可求三角形面积之和，这两种思维方式切入的路径虽然有别，但都融入了一个化未知为已知的转化思想.用含字母m的式子表示字母S，涉及代数式的布列及其运算，体现了建模思想；第（Ⅲ）问求m的值，可归结为由函数值求自变量的值，实则是解方程，但要注意函数式中的自变量的取值范围.求出m值后需验证该值是否在函数自变量m的取值范围内.缺乏解后验证是绝大多数学生此问失分的主要原因，故求函数解析式的同时应注意到自变量的取值范围.

二、试题解答

（Ⅱ）方法1：由局部到整体联想到三角形面积的和、差化法.

因为∠A=∠A′=30°，所以∠CMO=∠A+∠A′=60°.

方法2：由大化小联想到图形面积的分割法.

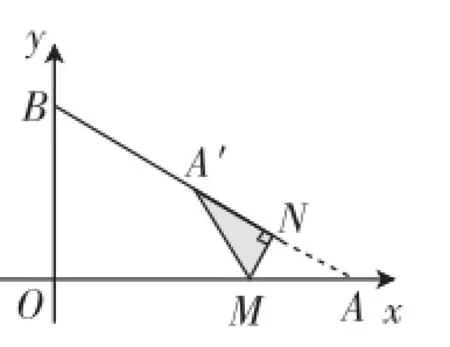
图3

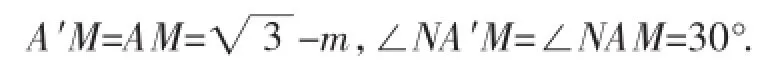
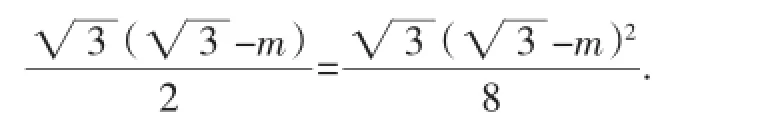
三、解析之感——在寻求不同切入点中优化学生思维品质

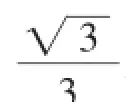
经一番拼搏完成一题后自然是高兴的，高兴之余还要静下心来及时跟进，想一想：此问是否为特殊情形，图形中还蕴藏着哪些有价值的信息而没有被发现和揭示出来，对接下来一问的解题思路有无铺垫和启发的作用，还有无其他情况和继续拓展的空间；除此方法之外，还有无其他的方法，若有其他方法，这些方法之间在数学思想的应用上有无共同“语言”.案例中的每一问都给出了两种方法，体验到思考问题的多视角；解题后的验证是一种思维的反思，能弥补因一时不周而造成的缺陷，提高解题的准确性，所以解题后验证是解题成功的一个重要环节.H