基于非局部全变差和部分支撑已知的CS-MR图像重建方法

赵地，杜慧茜，韩宇，梅文博

(北京理工大学 信息与电子学院，北京 100081)



基于非局部全变差和部分支撑已知的CS-MR图像重建方法

赵地，杜慧茜，韩宇，梅文博

(北京理工大学 信息与电子学院，北京 100081)

提出一种基于压缩感知(CS)的磁共振(MR)图像重建方法.利用参考图像和目标图像结构的相似性，提取参考图像在小波域中L个大系数的索引集作为目标图像的已知支撑集，约束已知支撑集补集中小波系数的l1范数.此外，采用非局部全变差(NLTV)作为规整化项构造目标函数，通过快速合成分离算法(FCSA)重建目标图像.仿真结果证明，该方法能有效保留图像的边缘和细节信息，抑制噪声干扰，在相同采样数据量下，重建性能优于经典CS-MRI和其他同类方法.

核磁共振成像；压缩感知；非局部全变差；Modified-CS；快速合成分离算法

核磁共振成像(magnetic resonance imaging，MRI)技术在医学诊断中起着重要的作用，然而由于成像设备的物理特性和人体本身的生理特点等因素，成像速度慢，数据采集时间长是多年来难以突破的瓶颈.近年来提出的压缩感知理论(compressed sensing，CS)[1-3]利用信号的稀疏性作为先验信息，可以由少量观测值精确地恢复原信号.将CS理论应用到MRI领域可在保证成像质量的前提下，大幅缩短扫描时间，提高成像速度[4-7].Lustig等[4]首先提出了基于CS的MR图像重建模型(以下称经典的CS-MRI模型)：

(1)

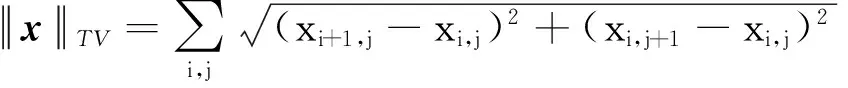
经典的CS-MRI只利用了图像的稀疏特性.而在实际的MRI应用中，往往需要在同一场景下不同时间段获取多幅MR图像.这种情况下，获取的多幅图像之间有着非常相似的结构，高分辨率参考图像可以为目标图像的重建提供更多的先验信息，从而进一步降低采样数据量.如文献[8-10]就是将目标图像建模为参考图像与差异图像的组合，利用差异图像的稀疏性，将目标图像的重建问题转化为对差异图像的CS重建.

不同于上述方法，本文不引入差异图像，而是直接利用目标图像与参考图像的结构相似性提出一种新的重建模型.模型中包括数据保真项和两个规整化项.由于目标图像与参考图像的结构相似，本文将参考图像在小波域中大系数的索引集作为目标图像的已知支撑集，约束已知支撑集补集中小波系数的l1范数，以降低采样数据量.同时还约束目标图像的非局部全变差(nonlocal total variation，NLTV)[11-13]，目的是为了保持图像边缘及细节信息，避免TV规整化引起的块状效应和图像质量的退化.本文提出的重建模型包含两个非光滑的规整化项，传统的求解方法(如共轭梯度法[4]，偏微分方程法[14])收敛速度慢，制约着MR成像的速度.本文采用近年来由J.Huang等[12，15]提出的快速合成分离算法(fast composite splitting algorithm，FCSA)求解目标图像.该算法将复杂的复合规整化问题分解为多个简单的子问题并行求解，收敛速度快，能够在提高重建精确度的同时降低计算的复杂度.仿真结果证明，本文方法在重建性能上优于经典方法和其他同类方法，可以在保证重建质量的前提下，进一步降低采样数据量，提高成像效率.

1 重建方法

1.1 重建模型

本文基于参考图像和目标图像之间结构的相似性，利用参考图像获取先验信息，并结合NLTV的优势，提出一种新的MR图像重建模型：

(2)

重建模型中第2项的理论依据来自N.Vaswani[16]提出的Modified-CS.该理论证明，若已知信号的部分支撑，则可通过约束该信号在已知支撑集补集上的l1范数，获得相同测量率下更为精确的重建.已知支撑集信息的获取需要根据实际应用确定.由于参考图像与目标图像具有结构相似性，其小波域支撑中具有较大幅值的小波系数遵循近似相同的分布，因此，参考图像Ir在小波域中的大系数的索引集可视为目标图像的已知支撑集T.本文约束目标图像在Tc上的l1范数作为规整化项，以提高重建精确度.

式(2)中第3项约束目标图像的NLTV范数，此规整化项可有效克服经典TV规整化带来的块状效应，保持图像的边缘及细节信息，同时抑制噪声干扰.对一幅定义在Ω上的图像x，其NLTV定义为[11-12]

(3)

式中：x(u)和x(v)表示像素u和v处的像素值(u和v为二维向量，表征像素点坐标).权重函数w(u，v)表征像素点u和v之间的差异被惩罚的程度，由下式给出：

(4)

其中，

(5)

(6)

定义了以像素u和v为中心，大小为m×m(m为奇数)的图块qx(u)和qx(v).

由式(4)定义的权重函数度量了图块qx(u)和qx(v)的相似性.对于每一对(u，v)，权重w(u，v)为标量，且具有非负性和对称性，即w(u，v)=w(v，u).Zx为归一化因子，参数σ制约图块间的相似程度.

经典TV仅考虑相邻像素点间的作用，故具有“局部性”.而式(3)定义下的NLTV，除考虑相邻像素点外，还包含更大范围(甚至整个图像域)，“非局部”的命名也由此而来.

1.2 算 法

对于经典的CS-MRI重建，一幅256×256的图像就需求解数万个参数，对于此类复杂的大规模优化问题，前人多采用共轭梯度法，偏微分方程法等求解，然而这些算法收敛速度慢，计算复杂度高，严重制约了其在实际MRI中的应用.近年来提出的TVCMRI[17]和RecPF[18]方法可以实现经典的CS-MRI图像的快速重建，但并未给出关于计算复杂度边界的理论证明.本文采用更为先进的FCSA算法求解所提出的重建问题，该算法基于变量可分离和算子可分离技术，将复杂的复合规整化问题分解为两个简单的子问题并行求解，然后对子问题的最优解进行加权平均，经过若干次迭代重建出目标图像.每次迭代中的复杂度边界为O(plogp)，其中p为待重建图像的像素个数[15].

应用FCSA算法求解本文重建模型的步骤如下：

步骤1 对参考图像进行小波分解，选取最大的L个小波系数的索引集作为目标图像的已知支撑集T.

fork=1toKdo

xg=rk-ρ

end for

上述算法中有关记号和函数的定义说明如下：

② 关于连续的凸函数g(x)的近似映射(proximalmap)定义为

(7)

式中ρ>0为标量.

③ 投影函数x=project(x，[l，u])定义为

(8)

由于本文中所用图像均为8-bit的灰度MR图像，因此选取l=0，u=255.

2 实验结果与分析

本文实验均在Matlab2011b环境下运行，PC平台配置为Pentium E5300，2.6 GHz CPU，2 GB内存.实验中所用MR图像的尺寸均为256×256.为了评估本文方法的重建性能，并分析参考图像提供的支撑信息和NLTV规整化项对重建的贡献，选取两组实际的MR图像进行仿真实验，并与下列3种方法进行比较：

① 经典的CS-MRI重建方法[4]，即式(1).

②l1-NLTV方法[12]，重建模型如式(9)：

(9)

③ Modified-CS-TV方法，重建模型如式(10).

(10)

以上各重建方法均采用FCSA算法求解，选定参数ρ=1.本文实验采用如图1所示的变密度采样模板获取k空间数据.NLTV中图块大小都选定为5×5(即m=5).对多幅MR图像进行实验可知，一般选择参考图像最大的前20%小波系数为目标图像提供已知支撑.

2.1 实验1

首先选取图2(a)为参考图像，2(b)为待重建的目标图像，它们来自同一病人脑部扫描序列.

图3显示了10%测量率下各种方法的重建结果.此实验中，选取参考图像最大的L=10 036个小波系数对应的索引集作为目标图像在小波域的已知支撑集，规整化参数λ=10-2，α=5×10-3.

从图3所示的实验结果可以看出，由于采样数据量有限，经典的CS-MRI方法无法获得清晰的重建图像.NLTV规整化项的引入，使l1-NLTV方法的重建性能有所提升，重建结果证明了NLTV较TV能更好地保持边缘及细节信息，并有效抑制噪声，提高信噪比.Modified-CS-TV方法利用了参考图像的支撑信息，重建质量较经典的CS-MRI方法也有明显改善.图3(d)为本文方法的重建结果，将NLTV和Modified-CS结合，利用更多的先验信息约束重建，同时消除了TV带来的块效应，获得了最好的重建效果.

表1列出了上述4种方法在10%测量率下重建目标图像的相对误差和峰值信噪比(PSNR)，表中数据也充分说明了本文方法的优越性.

图4中的曲线比较了各种重建方法在不同测量率下的相对误差，结果表明本文方法均能取得最好的重建结果.尤其是在低测量率下，优越性更为显著(在不同测量率下规整化参数的选取略有不同，范围为λ=10-3～10-2，α=5×10-3).

表1 各种方法重建图像的相对误差与PSNR

Tab.1 Relative errors and PSNR values of reconstructed images by different methods

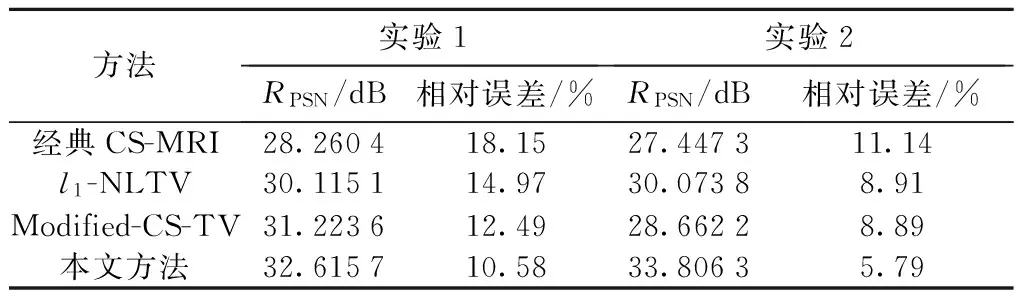
方法实验1实验2RPSN/dB相对误差/%RPSN/dB相对误差/%经典CS-MRI28.260418.1527.447311.14l1-NLTV30.115114.9730.07388.91Modified-CS-TV31.223612.4928.66228.89本文方法32.615710.5833.80635.79

2.2 实验2

本组实验选取图5(a)为参考图像，5(b)为目标图像.参考图像与目标图像之间存在对比度差异以及局部形变.图6和表1显示了15%测量率下各方法的重建结果.此处，选取参考图像在小波域中最大的10 536个系数的索引作为目标图像的已知支撑集，规整化参数λ=8×10-3，α=10-3.

重建结果显示出和上一组实验类似的结论.本文方法无论在相对误差数值还是视觉效果上都取得了最优的重建结果.由于扫描成像设备的局限性，原始目标图像中存在噪声，从重建图像可以看出，本文方法在很好地保留图像信息的前提下，一定程度上抑制了噪声干扰，提升了图像的视觉质量.

图7中的曲线显示了不同测量率下各种方法重建图5(b)得到的重建结果的相对误差(规整化参数选取范围为λ=10-3～10-2，α=10-3).从图中曲线可知，4种方法的重建误差都随着测量率的提高明显降低，而本文方法在不同测量率下均具有最低的重建误差.这充分说明，所提出的重建方法有效可行，能够在保证重建质量的前提下，进一步减少采样数据量.

本文给出了两组实验中规整化参数在不同测量率下的取值范围.多组MR图像重建实验验证，对同一目标图像，不同测量率下，最优规整化参数的选取在一定范围内具有鲁棒性，即选择同样参数，本文方法仍可在各测量率下获得优于经典CS-MRI及其他同类方法的重建性能.

3 结 论

本文提出一种新的利用参考图像结构信息的CS-MRI重建方法.利用已获取的高分辨率参考图像与待重建目标图像之间的结构相似性，从参考图像中提取目标图像的已知支撑集，以降低采样数据量.此外，该方法使用NLTV规整化，克服了经典的TV规整化带来的块状效应以及边缘和细节信息丢失的问题.实验结果表明，本文方法的重建性能优于经典的CS-MRI方法以及其他同类方法，能够在保证重建质量的同时进一步降低测量率，提高MRI成像速度.对于实际的MRI应用(动态MRI，介入式治疗等)和其他成像领域，具有实用价值.

[1] Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory，2006，52(4):1289-1306.

[2] Donoho D L，Elad M，Temlyakov V N.Stable recovery of sparse overcomplete representations in the presence of noise[J].IEEE Transactions on Information Theory，2006，52(1):6-18.

[3] Candes E J，Romberg J，Tao T.Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory，2006，52(2):489-509.

[4] Lustig M，Donoho D L，Pauly J M.Sparse MRI: the application of compressed sensing for rapid MR imaging[J].Magn Reson Med，2007，58(6):1182-1195.

[5] Jung H，Sung K，Nayak K S，et al.k-t FOCUSS: a general compressed sensing framework for high resolution dynamic MRI[J].Magn Reson Med，2009，61(1):103-116.

[6] Trzasko J，Manduca A.Highly undersampled magnetic resonance image reconstruction via homotopicl0-minimization[J].IEEE Transactions on Medical Imaging，2009，28(1):106-121.

[7] Haldar J P，Hernando D，Liang Z P.Compressed-sensing MRI with random encoding[J].IEEE Transactions on Medical Imaging，2011，30(4):893-903.

[8] Du H Q，Lam F.Compressed sensing MR image reconstruction using a motion-compensated reference[J].Magn Reson Imaging，2012，30(7):954-963.

[9] Peng X，Du H Q，Lam F.Reference-driven MR image reconstruction with sparsity and support constraints[C]∥IEEE International Symposium on Biomedical Imaging.Chicago，USA: [s.n.]，2011:89-92.

[10] Lam F，Haldar J P，Liang Z P.Motion compensation for reference-constrained image reconstruction from limited data[C]∥IEEE International Symposium on Biomedical Imaging.Chicago，USA: [s.n.], 2011：73-76.

[11] Zhang X Q，Chan T F.Wavelet inpainting by nonlocal total variation[J].Inverse Problems and Imaging，2010，4(1):191-210.

[12] Huang J，Yang F.Compressed magnetic resonance imaging based on wavelet sparsity and nonlocal total variation[J].IEEE International Symposium on Biomedical Imaging (ISBI).Barcelona: [s.n.]，2012:968-971.

[13] Lou Y，Zhang X，Osher S，et al.Image recovery via nonlocal operators[J].Journal of Scientific Computing，2010，42:185-197.

[14] He L，Chang T C，Osher S，et al.MR image reconstruction by using the iterative refinement method and nonlinear inverse scale space methods[R].[S.l.]: UCLA CAM，2006.

[15] Huang J，Zhang S，Metaxas D.Efficient MR image reconstruction for compressed MR imaging[J].Medical Image Analysis，2011，15:670-679.

[16] Vaswani N，Lu Wei.Modified-CS: modifying compressive sensing for problems with partially known support[J].IEEE Transactions on Signal Processing，2010，58(9):4595-4607.

[17] Ma S，Yin W，Zhang Y，et al.An efficient algorithm for compressed MR imaging using total variation and wavelets[C]∥Proceedings of Conference on Computer Vision and Pattern Recognition.Anchorage，USA：IEEE，2008:1-8.

[18] Yang J，Zhang Y，Yin W.A fast alternating direction method for TVL1-L2 signal reconstruction from partial Fourier data[J].IEEE Journal of Signal Processing，2010，4(2):288-297.

(责任编辑：刘芳)

Compressed Sensing MR Image Reconstruction Based on Nonlocal Total Variation and Partially Known Support

ZHAO Di，DU Hui-qian，HAN Yu，MEI Wen-bo

(School of Information and Electronics，Beijing Institute of Technology，Beijing 100081，China)

By exploiting the similarity of the structure between the reference and the target images, a novel compressed sensing (CS)-based reconstruction method was proposed for MR image.Indexes of theLlargest wavelet coefficients of the reference image were extracted and regarded as the known part of the desired target image’s support, and thel1norm of the wavelet coefficients belonging to the complement to the known support was constrained.Furthermore, the nonlocal total variation (NLTV) was utilized as a regularization term to construct the objective function.Then the target image was reconstructed via a fast composite splitting algorithm (FCSA).Experimental results demonstrate that the proposed method can preserve edges and details while suppressing noise efficiently.It outperforms conventional CS-MRI and other similar reconstruction methods under the same sampling rate.

magnetic resonance imaging;compressed sensing;nonlocal total variation;Modified-CS;fast composite splitting algorithm

2013-10-21

国家自然科学基金资助项目(61077022)

赵地(1986—)，女，博士，E-mail:dizhao0811@163.com.

杜慧茜(1972—)，女，博士，副教授，E-mail:duhuiqian@bit.edu.cn.

TP 391

A

1001-0645(2016)03-0308-06

10.15918/j.tbit1001-0645.2016.03.016