表面形貌对应力集中系数的影响研究
程正坤,廖日东,李玉婷,侯世远
(北京理工大学 机械与车辆学院,北京 100081)
表面形貌对应力集中系数的影响研究
程正坤,廖日东,李玉婷,侯世远
(北京理工大学 机械与车辆学院,北京 100081)
基于线弹性力学计算了机加工试样表面各点的应力分布,提出了等效应力集中系数的概念,该参量可以反映机加工表面的总体应力集中水平.采用谐波叠加的方式模拟表面形貌,提出了表面形貌有限元建模的新方法.分析了粗糙度的各表征参数对有效应力集中系数的影响.结果表明表面形貌各粗糙度表征参数对有效应力集中系数均具有明显的影响,各粗糙度表征参数与有效应力集中系数之间具有二次曲线拟合关系式.
表面形貌;有效应力集中系数;有限元
一般情况下,材料的疲劳强度随着表面粗糙度等级的提高而降低[1].表面形貌对疲劳特性的影响主要是由于表面形貌能产生应力集中,从而诱发疲劳裂纹的萌生,因此精确计算构件的表层应力分布对评估零件的疲劳特性至关重要.
针对表面形貌对应力集中系数的影响,Neuber[2]、Arola及Ramulu[3]分别给出了不同的半经验公式.研究表明,机加工表面形貌具有几何自相似和自仿射性,随着测量尺度和轮廓仪器分辨率的提高,表面形貌更精细的成分将会出现[4].而Neuber模型及Arola-Ramulu模型在预测表面形貌引起的应力集中系数时,均采用了粗糙度高度分布参数及轮廓谷底半径,这些表征参数与测量尺度及轮廓仪器分辨率密切相关.而且轮廓谷底半径的测量一般采用半径规,需测量关键的几个谷底的半径然后取平均值,这种测量方法操作困难且容易产生测量误差.后来,采用有限元方法分析表面形貌对应力集中系数的影响得到发展.Suraratchai等[5]采用样条插值函数拟合了实测机加工表面形貌,As等[6-7]采用贝塞尔插值函数拟合了磨削加工表面形貌,他们分别基于插值函数拟合的表面轮廓构建了实测表面形貌的有限元模型,然后基于线弹性力学分析了机加工表面形貌引起的应力集中系数.然而机加工表面形貌对疲劳特性的影响具有尺度效应,当表面粗糙度等级足够小的时候,机加工表面形貌对疲劳强度没有影响[8-10].因此在分析表面形貌对应力集中系数的影响时,表面形貌的高频成分可以不予考虑.
文中通过幅频特性分析提取出实际车削加工表面形貌的有用信息,然后采用谐波叠加的方式拟合了机加工表面形貌,提出了表面形貌有限元建模的新方法.基于线弹性力学计算了机加工试样表面形貌上各点的应力分布,提出了表面有效应力集中系数的概念,进一步分析了表面形貌的各表征参数与有效应力集中系数之间的关系.
1 表面形貌的模拟
机加工表面形貌可以看作是各态历经平稳的随机过程[8],可以通过幅频特性分析,提取表面形貌各阶谐波的幅值、频率和相位信息,然后采用谐波叠加的方式来模拟表面形貌.表面形貌可以拟合为
(1)
式中:W(x)为拟合表面形貌;Ai为第i阶谐波的幅值;fi为第i阶谐波的频率;φi是第i阶谐波的相位.实际测量的机加工表面形貌为Z(x),当拟合表面形貌W(x)满足方程(2)时,认为拟合表面形貌可以代替实际形貌来分析表面形貌对应力集中系数的影响.
(2)
式中cmin为会影响疲劳强度的最小粗糙度门槛值.
文献[10]表明,除掉机加工过程中产生的残余应力,机加工表面粗糙度参数Ra>0.1 μm将会对疲劳寿命有很大的影响.而当表面粗糙度参数Ra<0.1 μm,疲劳裂纹萌生源将由表面形貌轮廓谷底转向驻留滑移带或者晶粒边界位置,表面形貌对疲劳的影响将被消除.文中在模拟表面形貌时,将cmin值定为0.1 μm.
在本文研究中,车削加工了20根不同粗糙度等级的42CrMo高强度钢圆棒试样,然后采用TR300粗糙度测量仪对这20根圆棒试样沿轴线方向的表面形貌进行了测量.取样长度为4 mm,在取样长度范围内将粗糙度测量仪测得的表面形貌的数据点进行幅频特性分析,然后按式(2)要求提取所有有用的谐波信息,采用谐波叠加的方式拟合表面形貌.图1为粗糙度参数Ra=1.85 μm试样的表面形貌的幅频特性曲线,图2为该试样的表面形貌的拟合效果图.
2 表面形貌的有限元分析
在分析表面形貌对应力集中系数影响时,本文假定材料满足各向同性、均匀性假设,在计算应力集中系数时,只需考虑材料的线弹性行为.采用谐波叠加的方法拟合的表面形貌为高阶光滑函数,首先利用Abaqus软件建立了规则的有限元网格模型,通过Fortran语言编程更改有限元模型节点坐标,实现有限元模型表面为拟合的表面形貌函数W(x).网格类型为四边形二次完全积分单元.有限元模型中临近表面形貌的最小网格尺寸为1.3 μm.材料为42CrMo高强度钢,其弹性模量E=212 GPa,泊松比μ=0.28.
图3所示为表面形貌有限元网格模型,模型尺寸为4 mm×4 mm.均布拉伸载荷被施加在有限元模型左右两端边界上.提取表面形貌上所有节点沿加载方向的主应力,然后除以名义应力,可以得到表面形貌上各点的应力集中系数.图4所示为表面形貌与表面各点应力集中系数的对比图.

(3)
(4)
20根样件的表面形貌引起的最大应力集中系数及有效应力集中系数计算结果如表1所示.
表1 不同试件的粗糙度表征参数及应力集中系数
Tab.1 Roughness parameters and stress concentration factors of different specimens

试件Ra/μmRy/μmRz/μm ρ/μmKtmax KtβN11.8513.699.70451.661.470.0060N23.0713.3912.78371.681.510.0050N35.1922.1020.9592.482.040.0500N47.8232.7031.20282.151.860.0200N512.0647.8045.00202.732.560.0300N65.1925.7021.80212.291.970.0200N77.6331.5030.20142.502.130.0400N87.8832.0031.00222.171.880.0200N91.8815.509.60361.781.600.0100N101.9712.309.56362.051.620.0400N110.735.263.76421.391.280.0050N120.867.133.059201.091.030.0007N130.833.391.838501.171.060.0020N1411.6245.8943.68242.602.330.0500N1512.6751.3949.93302.542.230.0300N1612.2251.6847.56113.202.620.0500N1712.1851.8548.52202.552.390.0500N1812.4950.2448.24212.512.220.0300N191.689.817.20501.621.460.0040N201.609.286.98471.811.470.0160
表1结果表明,20根试件的有效应力集中系数的方差均控制在5%范围内,因此采用如式(3)所示的方法计算得到的有效应力集中系数能够有效表征车削加工试样表面整体应力集中水平.
拟合的表面形貌

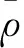
(5)
Neuber[2]提出了粗糙度对应力集中系数影响的一个半经验公式为
(6)
式中:Rz和ρ分别是微观不平度10点高度和缺口谷底曲率半径;λ为缺口间距与深度的比值.然而实际加工表面该λ很难测量,对于机加工表面,通常认为λ=1是合适的[11].根据式(6),Arola及Ramulu提出另一粗糙度对应力集中系数影响的半经验公式[3]为
(7)
采用半经验公式Neuber模型及Arola-Ramulu模型预测的20根试件的有效应力集中系数与基于有限元方法计算得到的有效应力集中系数进行对比,如图5所示.由图5可知,Arola-Ramulu模型及Neuber模型预测的结果与有限元计算的结果的相对误差大致能够控制在20%范围内,而Arola-Ramulu模型预测粗糙度引起的应力集中系数较为保守.
3 粗糙度表征参数对有效应力集中系数的影响
表面形貌的表征参数非常复杂,目前国际标准中用于描述二维表面形貌的粗糙度表征参数大致分为3类.① 高度分布参数,如轮廓算术平均偏差Ra、轮廓均方根偏差Rq、轮廓最大高度Ry、微观不平度10点高度Rz等;② 间距分布参数,如轮廓的平均波长Sm等;③ 混合特性参数,如轮廓的算术平均斜率Δa、轮廓的均方根斜率Δq、轮廓的算术平均波长λa、轮廓的均方根波长λq等.
目前粗糙度各表征参数对应力集中系数的影响鲜有报道,机加工表面形貌的粗糙度表征参数对应力集中系数的影响在本小节将得到详细的分析.本文分析机加工表面形貌对有效应力集中系数的影响时,实际测量的表面形貌的高频成分不予考虑,而表面形貌的粗糙度表征参数与轮廓仪器分辨率密切相关.在此,对拟合的表面形貌W(x)的各粗糙度表征参数进行计算,然后分析了拟合表面形貌W(x)的各粗糙度表征参数与有效应力集中系数之间的关系.
3.1 粗糙度高度分布参数对有效应力集中系数的影响
粗糙度高度分布参数对有效应力集中系数的影响如图6和图7所示.采用二次曲线拟合了粗糙度高度分布参数与有效应力集中系数之间的关系,如式(8)所示,相关系数分别为0.870,0.869,0.894,0.890.
(8)
3.2 粗糙度间距分布参数对有效应力集中系数的影响
粗糙度间距分布参数与有效应力集中系数的关系如图8所示.采用二次曲线拟合了粗糙度间距分布参数与有效应力集中系数之间的关系,如式(9)所示,相关系数为0.860.

(9)
3.3 粗糙度混合特性参数对有效应力集中系数的影响
粗糙度混合特性参数与有效应力集中系数的关系如图9~图10所示.采用二次曲线拟合了粗糙度混合特性参数与有效应力集中系数之间的关系,如式(9)所示,相关系数分别为0.921,0.912,0.789,0.788.
(10)
由图6至图10可以看出,尽管存在一定的离散性,但拟合表面形貌各粗糙度表征参数与有效应力集中系数之间相关性很明显,随着拟合表面形貌各粗糙度表征参数的增加,有效应力集中系数随之增加.
4 结 论
提出了表面形貌有限元建模的新方法,对20根车削加工圆棒试样的表面形貌进行了幅频特性分析,然后采用谐波叠加的方式拟合了表面形貌,基于线弹性力学分析了机加工表面形貌各点的应力分布,提出了有效应力集中系数的概念.得到以下结论.
① 采用Arola-Ramulu模型及Neuber模型预测的表面形貌引起的有效应力集中系数与本文所采用的有限元计算结果的相对误差大致能够控制在20%范围内,Arola-Ramulu模型预测表面形貌引起的应力集中系数较为保守.
② 尽管存在一定的离散性,但拟合表面形貌高度分布参数、间距分布参数及混合特性参数对有效应力集中系数均有很大影响.随着各粗糙度表征参数的增加,有效应力集中系数随之增加.采用数据拟合,各粗糙度表征参数与有效应力集中系数之间具有二次曲线关系.
[1] Bayoumi M R,Abdellatif A K.Effect of surface finish on fatigue strength[J].Engineering Fracture Mechanics,1995,51(5):861-870.
[2] Neuber H.Kerbspannungsleshre[M].Berlin: Springer Verlag,1958.
[3] Arola D,Ramulu M.An examination of the effects from surface texture on the strength of fiber reinforced plastics[J].Journal of Composite Materials,1999,33(2):101-86.
[4] Majumdar A,Tien C L.Fractal characterization and simulation of rough surfaces[J].Wear,1990,136(2):313-327.
[5] Suraratchai M,Limido J,Mabru C,et al.Modelling the influence of machined surface roughness on the fatigue life of aluminium alloy[J].International Journal of Fatigue,2008,30:2119-2126.
[6] As S K,Skallerud B,Tveiten B W,et al.Fatigue life prediction of machined components using finite element analysis of surface topography[J].International Journal of Fatigue,2005,27:1590-1596.
[7] As S K,Skallerud B,Tveiten B W.Surface roughness characterization for fatigue life predictions using finite element analysis[J].International Journal of Fatigue,2008,30:2200-2209.
[8] Aono Y,Noguchi H.Fatigue limit reliability of axisymmetric complex surface[J].International Journal of Fracture,2005,131:59-78.
[9] Miyazaki T,Aono Y,Noguchi H.A practical stress analysis for predicting fatigue limit of metal with axisymmetric complex surface[J].International Journal of Fracture,2007,143:355-367.
[10] Novovic D,Dewes R C,Aspinwall D K,et al.The effect of machined topography and integrity on fatigue life[J].International Journal of Machine Tools and Manufacture,2004,44:125-134.
[11] Arola D,Williams C L.Estimating the fatigue stress concentration factor of machined surfaces[J].International Journal of Fatigue,2002,24:923-930.
(责任编辑:孙竹凤)
Effect of Surface Topography on Stress Concentration Factor
CHENG Zheng-kun,LIAO Ri-dong,LI Yu-ting,HOU Shi-yuan
(School of Mechanical Engineering,Beijing Institute of Technology,Beijing 100081,China)
Machined surface topography was regarded as a stationary stochastic process, and the true surface topography was simulated by superposing series of cosine components by means of spectrum analysis.A new method was proposed to build a finite element model of surface topography.Based on linear elastic mechanics, the stress distribution induced by machined surface topography was investigated.And a concept of effective stress concentration factor was presented to reflect the total degree of stress concentration of machined surface topography.Moreover, the effect of each roughness parameter on effective stress concentration factor was analyzed.The results show that each roughness parameter of surface topography has an obvious effect on the effective stress concentration factor and there is a relation between the effective stress concentration factor and the various surface roughness parameters, which can be described with approximate quadratic equations.
surface topography;effective stress concentration factor;finite element
2014-07-24
国家部委基金资助项目(20140701)
程正坤(1986—),男,博士生,E-mail:zhengkun2009@bit.edu.cn.
廖日东(1972—),男,教授,博士生导师,E-mail:liaord@bit.edu.cn.
TH 123.4
A
1001-0645(2016)03-0231-06
10.15918/j.tbit1001-0645.2016.03.003

