三连杆双足步行机器人结构建模与运动分析

孙玲玲，赵俊卿，王　亭

（山东建筑大学理学院，山东济南250101）

三连杆双足步行机器人结构建模与运动分析

孙玲玲，赵俊卿*，王亭

（山东建筑大学理学院，山东济南250101）

双足机器人具有与人类相似的步行运动方式，对环境具有较好的适应能力，在机器人研究与应用中具有重要的地位。文章基于三连杆结构双足步行机器人模型，运用三次函数模拟其直线运动步态，运用拉格朗日方程描述其关节力矩，建立了机器人的运动学和动力学模型，阐明了机器人运动过程状态与关节力矩的变化规律及特点。结果表明：机器人支撑腿力矩为-350～350 N·m远大于摆动腿力矩；躯干倾角对各关节驱动力矩的影响比较复杂，即使躯干保持竖直，其驱动力矩也会在-130～130 N·m之间变化；增大步行速度，各关节力矩都会相应增大；躯干倾角对各关节驱动力矩的影响比较复杂，在实际应用中需要借助合理的驱动方法稳定驱动力矩，实现机器人整体的平稳运动。

分析力学；三连杆步行机器人；结构建模；步态规划；关节力矩

0　引言

在高危与复杂环境下，机器人以其独特的优势，成为代替人类作业的重要工具。与轮式或者履带式机器人相比，双足步行机器人具有更好的适应地面环境的能力，成为近年来研究的热点。双足步行机器人的研究涉及力学、仿生学、机械控制理论与控制工程、传感器信息融合、计算机图形学等多门学科，具有十分重要的学术意义和应用价值［1-4］。

随着机械设计与传感技术的不断发展，机器人研究的瓶颈问题已经不在于样机的研制，而是步行基础理论的突破。为此，国内外学者开展了大量的研究工作。宋宪玺建立了双足机器人的混杂动力学模型，并对三连杆平面双足机器人的运动进行了仿真［1］；槐创锋等建立了双足步行机器人腿的可参数化仿真模型，并分析了影响机器人稳定性能的参数［2］；乌海东等分析和配置了双足机器人的腿部自由度，以通用性的原则设置驱动器，生成了运动动画［3］；史耀强搭建了双足机器人的实验平台，并进行了多关节规划动作调试与分析［4］；曾鹤基于预观控制的仿人机器人的线性步态规划，通过倒立摆模型建立双臂摆动产生力矩与摆动角度之间的数学关系，控制生成的摆动角轨迹［5］；王健美等基于Matlab对双足机器人进行动力学仿真与仿生控制，实现了双足机器人低能耗的稳定行走［6］；贠今天等采用三次样条插值方法规划机器人的前向运动，得到各关节的平滑运动轨迹［7］；Farshimi等提出了一种被动双足机器人模型，并进行运动方程的推导与模拟参数的分析［8］；Liu等使用最优控制律并结合弹道参数的优化方法和微分动态规划，对五连杆双足机器人进行了行走控制仿真与评估［9］。可以看出，尽管研究人员对不同的机器人结构，采用不同的基础理论和研究方法，从不同的角度进行了探索，但系统、精确的数学模型还比较缺乏。

步行基础理论的突破需要建立在系统、完善的基础理论之上。基于人类双足运动的内在特点，建立精确的数学模型描述机器人的运动，是深入研究机器人步行理论、进行稳定性分析与控制的基础［10-16］。双足机器人的结构可以采用三、五、七、九连杆等多连杆模型［1-5，9］。文中采用三连杆结构，基于拉格朗日方程建立其动力学方程，用三次函数拟合其腿部运动，得到描述双足步行机器人运动的精确数学模型，并分析了其运动状态。对于更复杂结构机器人的运动描述，该理论具有重要的推广应用价值。

1　结构模型及建模

三连杆机器人结构模型如图1所示，AC和BC分别为机器人的支撑腿和摆动腿，长度分别为l1和l2，质量分别为m1和m2则l1=l2，m1=m2；机器人的上身用躯干CD表示，其长度为l3，质量为m3。为简便起见，假定腿部和躯干均为质量均匀分布的刚性连杆，因而AC、BC和CD的质心C1、C2、和C3分别位于相应连杆的中点。

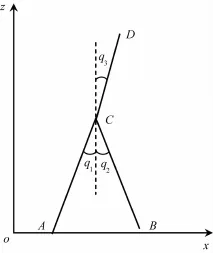
图1　三连杆机器人结构模型图

根据人体运动学资料，以中国中年男子为例，在竖直站立时，其重心在竖直方向的高度约为身体高度的55%～65%，并且重心位置随着运动状态发生变化［17］。假定三连杆机器人竖直站立时的重心位于髋关节C点以上、躯干CD的重心以下某处，即由式（1）表示为

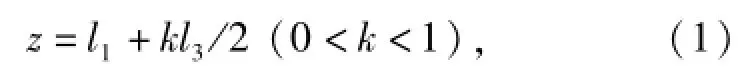
式中：z为重心，m；l1、l3分别为支撑腿长度与躯干长度，m；k为比例系数。

由质心的定义得到支撑腿与躯干质量分别由式（2）、（3）表示为

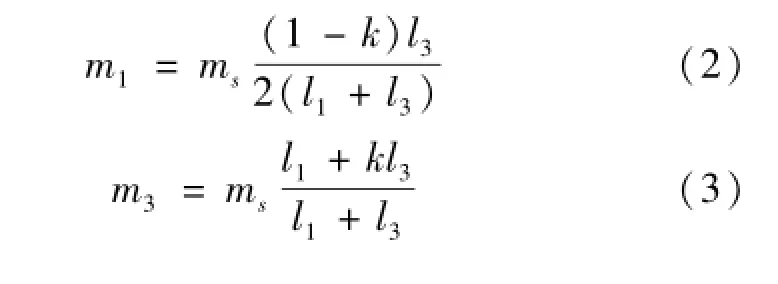
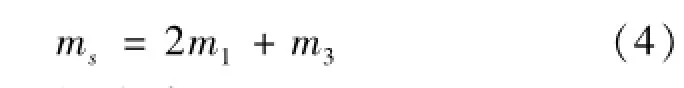
式中：ms为机器人的总质量，kg。

在计算中k为0.2，l1为0.55 m，l3为0.45 m，则m1为0.18 ms，m3为0.64 ms，重心位于身体高度的59.5%处，与管志光的研究结果相吻合［17］。

假定机器人在水平地面上沿x轴方向做步行运动，步行周期为T，步长为S。在任意时刻t，支撑腿AC、摆动腿BC和躯干CD的取向分别用角度q1、q2和q3表示，方向以y轴方向为正，如图1所示。支撑腿最大取向角用q0表示，在摆动脚着地的瞬间，设q1=-q2=q0，此时A、B的间距即为步长S。

在每个步长范围内，支撑腿的取向角q1用三次函数式（5）表示为

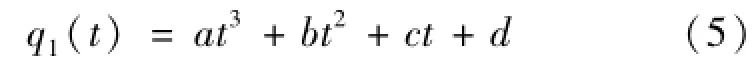
式中：t为时间，s；a、b、c、d为比例系数。

若q1（t）=-q2（t），且q1（0）=q0，q1（T/2）=0，q1（T）=-q0，则q1由式（6）表示为

考虑某个步行周期，设在任意时刻t，支撑腿AC位于角位置q1（t），角速度为，则支撑腿的动能由式（7）表示为

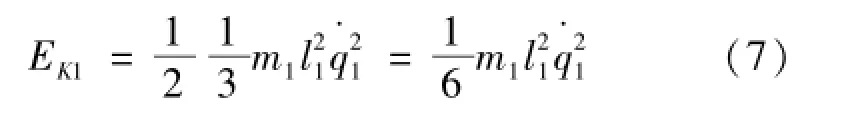
式中：Ek1为支撑腿动能，J；为支撑腿角速度，rad/ s。

以水平地面作为零势面，支撑腿的势能由式（8）表示为

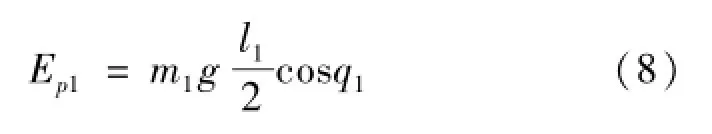
式中：Ep1为支撑腿势能，J；g为重力加速度，m/s2。对于摆动腿BC，其质心速度由式（9）表示为

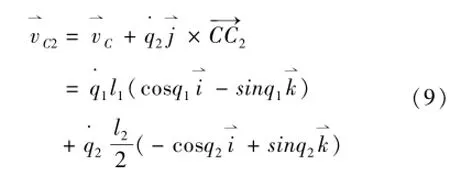
摆动腿的动能由式（10）表示为

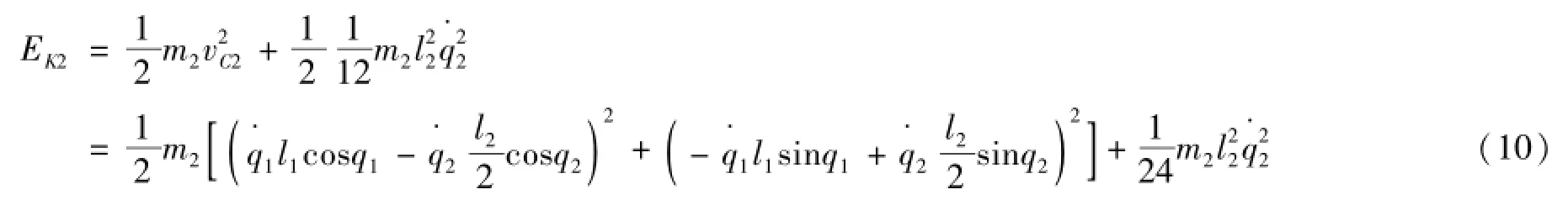
式中：Ek2为摆动腿动能，J。

摆动腿的势能由式（11）表示为

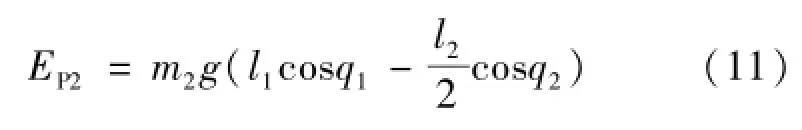
式中：Ep2为摆动腿势能，J。

对躯干CD，其质心速度由式（12）表示为

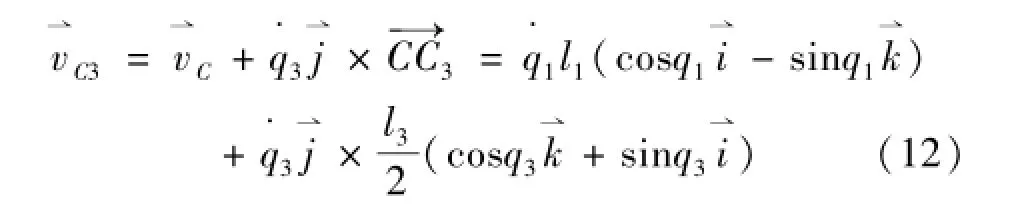
躯干的动能由式（13）表示为

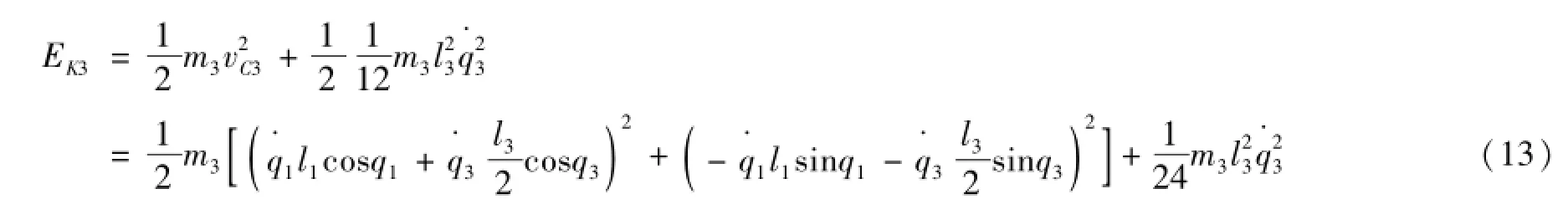
式中：Ek3为躯干动能，J。

躯干的势能由式（14）表示为

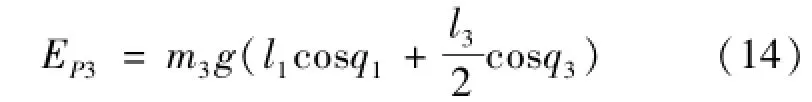
式中：Ep3为躯干动能，J。

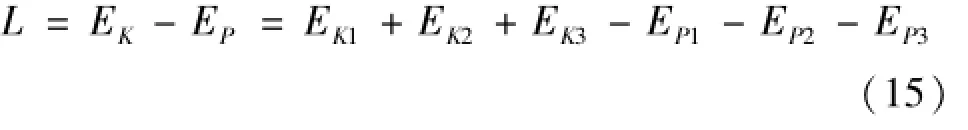
式中：Ek为系统总动能，J；Ep为系统总势能，J。

将拉格朗日函数分别对其自变量求导，得到式（16）～（21）为

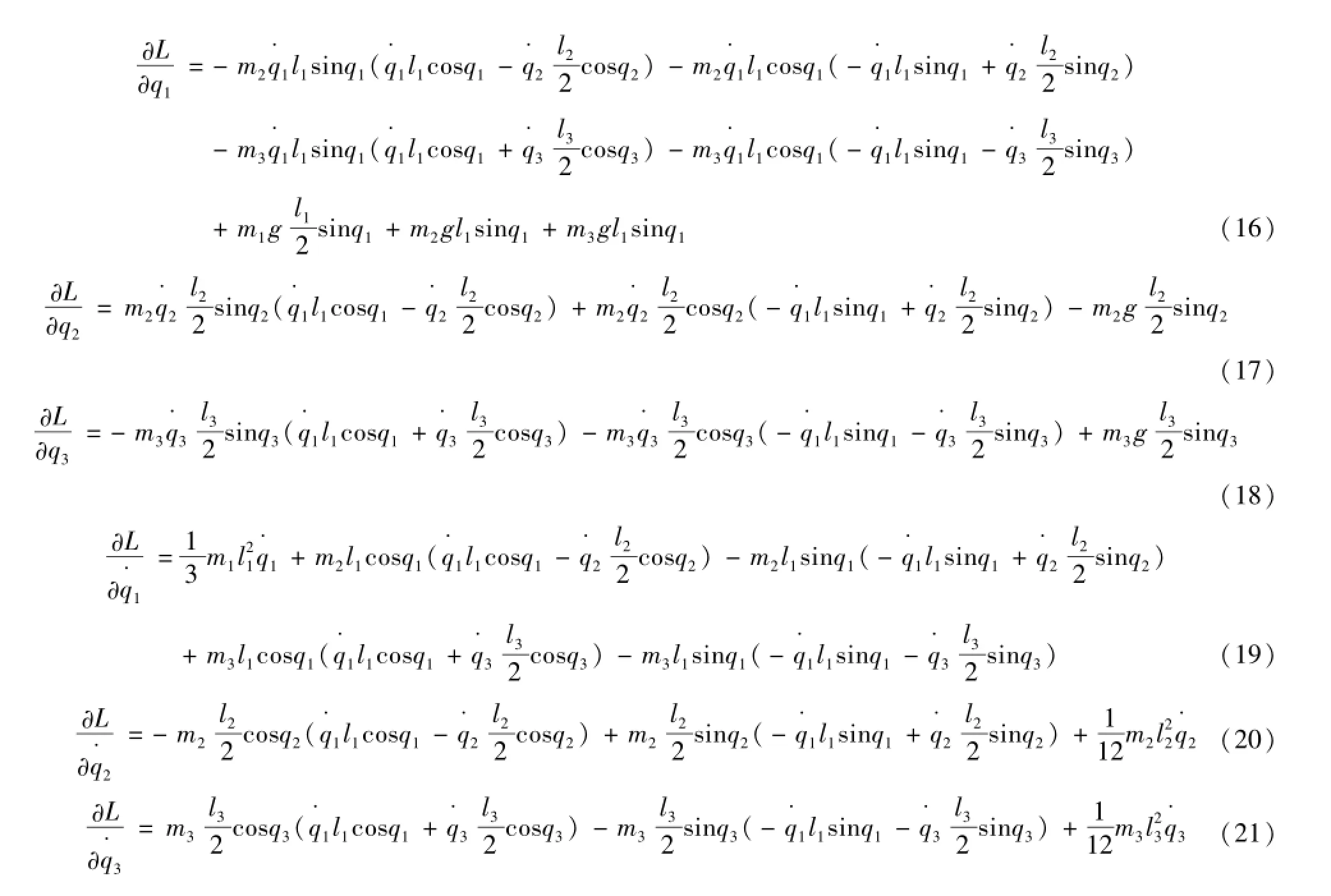
代入拉格朗日方程，各关节力矩由式（22）表示为

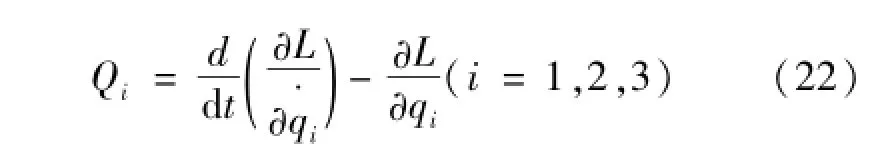
式中：Qi为各关节力矩，N·m；qi为各关节的角位置，°；为各关节的角速度，rad/s。

取i=1，得到支撑腿力矩Q1由式（23）表示为

取i=2，得到摆动腿力矩Q2由式（24）表示为

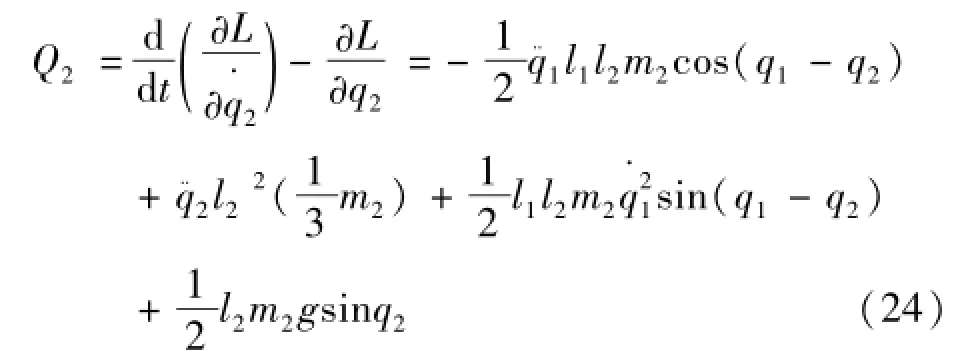
取i=3，得到躯干力矩Q3由式（25）表示为

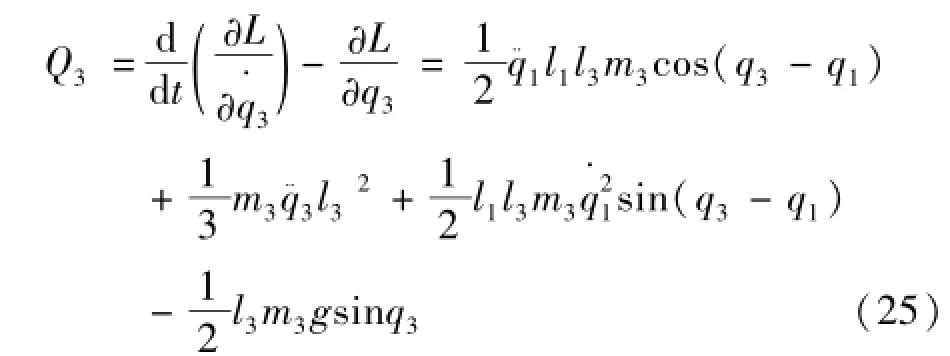
最终可将驱动力矩写成矩阵形式，由式（26）表示为

式中：

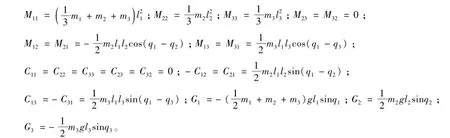
将式（26）简记为式（27）为

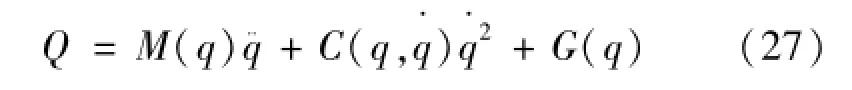
式中：M（q）是3×3的对称矩阵，称为系统的惯性矩阵；C（q）是3×3的反对称矩阵，与离心力和科氏力有关；G（q）是3×1的矩阵，为重力项。式（27）反映了关节力矩与关节变量、速度、加速度之间的关系。

2　模拟运动分析

取机器人总质量ms=50 kg，躯干取向角q3= 0°，步行周期T=3 s，支撑腿最大取向角q0=15°进行计算，计算结果如图2、3所示。由图2可知，在一个步长周期内，随着时间的延续，支撑腿取向角由q0变为，即向步行前方摆动30°。摆动角速度与y轴方向相反因而为负值，如图3所示，角速度大小在起、停时刻为0，t=T/2时最大，接近步长中心时角速度变化趋缓。

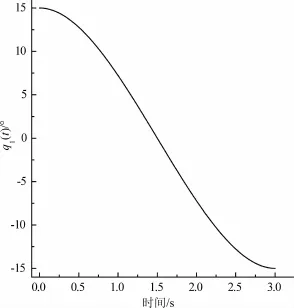
图2　支撑腿的角位置图

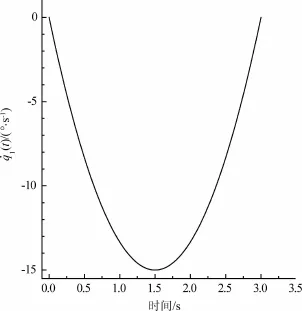
图3　支撑腿的角速度图

机器人的各关节力矩如图4所示。当T=3 s时，由图4（a）可以看出，支撑腿力矩范围为-350～ 350 N·m，摆动腿力矩为-85～85 N·m，支撑腿力矩远大于摆动腿力矩；竖直躯干的驱动力矩为-130～130 N·m之间，即使躯干保持竖直，随着腿部的摆动，作用于躯干的力矩也会随着时间发生变化。改变步行周期，取T=2 s，得到各关节的驱动力矩如图4（b）所示，可以看出，步行周期缩短为2 s，三个驱动力矩都相应增大，说明加快步行速度，需要增大各关节驱动力矩。

图4　支撑腿、摆动腿与躯干的关节力矩图

改变躯干的姿态，取躯干向步行前方倾斜的角度q3为0、3、6、9°，周期T=3 s，计算结果如图5所示。可以看出，躯干倾角对驱动力矩的影响是比较复杂的。在t1=0.25 s和t2=2.73 s附近，曲线相交于一点，在相交点前后不同的时间段，驱动力矩随躯干倾角的变化呈现出不同的趋势，随着躯干倾斜角度的增大，驱动力矩也相应增大，达到最小值与最大值的时间也相应提前。

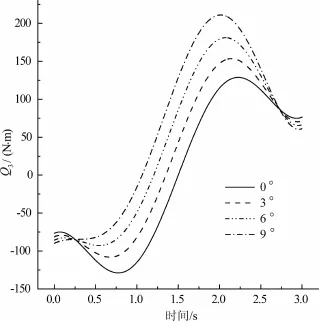
图5　躯干前倾角度对驱动力矩的影响图

3　结论

通过上述研究可知：

（1）三连杆双足步行机器人模型结构简单，图像清晰，能够较好地反映三次函数和拉格朗日方程在机器人运动学和动力学状态描述中的应用；通过改变机器人的质量、行走周期、躯干倾角、腿部摆动幅度等参量，可以实现对不同要求的机器人的控制，对于更复杂结构机器人的结构设计与运动控制具有一定的参考价值。

（2）当机器人总质量ms为50 kg，躯干取向角q3为0°，步行周期T为3 s，支撑腿最大取向角q0为15°时，支撑腿角速度在0～15°/s范围内平缓变化；支撑腿力矩在-350～350 N·m范围内变化，远大于摆动腿力矩变化范围-85～85 N·m；尽管躯干保持竖直，但其驱动力矩随着腿部的摆动在-130～130 N·m之间变化。通过缩短步行周期加快步行速度，各关节驱动力矩都相应增大。躯干倾角对各关节驱动力矩的影响比较复杂，在实际应用中需要借助合理的驱动方法稳定驱动力矩，辅之以躯干的灵活变化，实现机器人整体的平稳运动。

［1］ 宋宪玺.双足机器人的建模与稳定性分析［D］.合肥：中国科学技术大学，2010.

［2］ 槐创锋.方跃法.5连杆双足机器人建模和控制系统仿真［J］.系统仿真学报，2008，20（20）：5682-5686.

［3］ 乌海东，孔庆忠.双足机器人运动学分析与仿真［J］.机械制造与自动化，2014，43（1）：171-173，186.

［4］ 史耀强.双足机器人步行仿真与实验研究［D］.上海：上海交通大学，2008.

［5］ 曾鹤.仿人机器人的步态规划和步行控制研究［D］.广州：广东工业大学，2014.

［6］ 王健美，付成龙，黄元林，等.基于Matlab的双足机器人动力学仿真及仿生控制平台［J］.系统仿真学报，2011，23（5）：977-983.

［7］ 贠今天，杜萌萌，桑宏强，等.双足机器人结构设计与步态规划［J］.天津工业大学学报，2014，33（5）：80-83.

［8］ Farshimi F.，Naraghi M..A passive-biped model with multiple routes to chaos［J］.Acta Mechanica Sinica，2011，27（2）：277-284.

［9］ Liu C.G.，Atkeson C.G.，Su J.B..Neighboring optimal control for periodic tasks for systems with discontinuous dynamics［J］. Science China-Information Sciences，2011，54（3）：653-663.

［10］周雪峰.六自由度双足机器人步行研究［D］.广州：华南理工大学，2011.

［11］张世龙.双足机器人的步态规划及稳定性研究［D］.无锡：江南大学，2014.

［12］彭胜军，税海涛，杨庆，等.双足步行机器人转弯步态规划及其实现［J］.信息与控制，2010，39（6）：783-788，800.

［13］赵瑞林，孟彦京，王聪慧.教学型双足步行机器人直线行走步态稳定规划方法［J］.工业仪表与自动化装置，2014（5）：63-66.

［14］薛方正，陈强，厚之成.基于CPG的双足机器人多层步行控制器设计［J］.控制与决策，2015，30（3）：467-472.

［15］柯文德.基于人体运动相似性的仿人机器人运动规划关键技术研究［D］.哈尔滨：哈尔滨工业大学，2013.

［16］Jo H.S.，Mir-Nasiri N..Development of minimalist bipedal walking robot with flexible ankle and split-mass balancing systems［J］.International Journal of Automation and Computing，2013，10（5）：425-437.

［17］管志光.人体重心动态测试系统的研究［D］.青岛：山东科技大学，2005.

Modeling and motion analysis of a three-rigid-rod biped walking robot

Sun Lingling，Zhao Junqing*，Wang Ting

（School of Science，Shandong Jianzhu University，Jinan 250101，China）

Biped robot has a similar walking motion pattern with human beings，so it has better adaptability to the environment，and plays an important role in the research and application of the robot.This paper based on the model of biped walking robot with three link structures，according to the description of the linear motion gait and the design of joint moment，through cubic functions and Lagrange equation，establishes the model of kinematics and dynamics，and mainly explored the changing rules and characteristics of the state and joint torque of the robot motion process.The results show thatthe scope of joint torque driving the supporting leg is-350 to 350 N·m，and greater than the swinging leg torque.The trunk angle effecting on the driving torque of each joint is more complex，and its scope of driving torque is-130 to 130 N·m.ncreasthe walking speed，each joint torque will increase accordingly.The research methods and results have a certain reference value for the design and motion control of a robot with a more complex structure.

analytical mechanics；three-rigid-rod walking robot；structure modeling；gait planning；joint torque

O313.7

A

1673-7644（2016）04-0366-06

2016-05-20

国家自然科学基金项目（11204161）

孙玲玲（1991-），女，在读硕士，主要从事理论力学应用和有机半导体材料与器件等方面的研究.E-mail：834285178@qq.com

*：赵俊卿（1964-），女，教授，博士，主要从事有机半导体材料与器件和理论力学应用等方面的研究.E-mail：zjq@sdjzu.edu.cn