偶应力热弹性介质控制方程的推导

李　龙，魏培君

（北京科技大学数理学院应用力学系，北京100083）

偶应力热弹性介质控制方程的推导

李龙，魏培君

（北京科技大学数理学院应用力学系，北京100083）

非Fourier热传导的Lord-Shulman广义热弹性理论中包含了双曲型热传导方程，并且在广义热弹性介质中考虑了其微结构特性，引入了偶应力张量，偶应力研究可反映出材料的微尺度力学效应。文章基于Lord-Shulman广义热弹性理论，从能量守恒定律出发，分析了偶应力热弹性介质中的运动平衡方程、本构方程、能量方程以及边界条件的推导过程，并由此获得偶应力热弹性介质的运动控制方程和温度控制方程具体形式。结果表明：与经典热弹性理论的控制方程相比，基于Lord-Shulman理论的偶应力热弹性介质控制方程中的机械场与温度场相互耦合，而且在温度控制方程中存在含有弛豫时间的项，可使热信号以波动的形式和有限速度传播；而且当偶应力材料参数和弛豫时间取为零时，控制方程退化为经典理论的形式。

偶应力弹性理论；Lord-Shulman理论；广义热弹性；非Fourier热传导

0　引言

对于常规条件下的非稳态热传导问题，通常采用Fourier热传导定律来描述热流密度与温度梯度之间的关系，而且其精确度可以接受［1］。但是在一些极端条件下，例如在温度急剧变化时，由于热平衡过程的建立需要一定的时间，这类超常规的热传导现象中物理过程的时间间隔比达到局部热平衡的更短，Fourier定律中的准平衡假设将出现问题。因此，基于Fourier定律的热传导模型就不能准确描述这类现象，需要建立考虑热传播速度有限的非Fourier热传导模型。而广义热弹性理论考虑了非Fourier热传导模型，消除了传统热弹性理论中热信号传播速度无限大的物理学悖论。其中，Lord-Shulman理论［2］、Green-Lindsay理论［3］和Green-Naghdi理论［4］是主要的广义热弹性理论。Lord理论将一个通量率项合并到热传导Fourier定律中，并带有1个弛豫时间，包含了存在热流率项的由Fourier热传导方程推导出的双曲型热传导方程，建立了热信号传播速度有限的广义理论［2］。Green-Lindsay理论被称作是与温度变化率相关的热弹性理论，在本构方程中引入了温度率项，当所研究的物体有一个对称中心时，并不违反经典的热传导Fourier定律［3］。Green-Naghdi理论中引入了熵平衡思想和热位移的概念，提出了克服热波无限速度传播缺陷的不等式［4］。不同于经典理论，广义热弹性理论包含了双曲型方程，使热信号以波动的形式传播，成为了该领域中的研究热点。Chandrasekharaiah对热弹性第二声理论和双曲型广义热弹性理论进行了综述［5-6］。田晓耕等总结了包括不同类型广义热弹耦合问题的研究、发展和求解方法等广义热弹性问题在最近10年的研究进展［7］。任康乐等基于Lord-Shulman广义热弹性理论选取温度和位移及其一阶导数作为状态变量，结合Laplace积分变换并采用状态空间法，建立了功能梯度材料的一维广义热弹性响应的层合模型［8］。郭攀等基于Lord-Shulman广义热弹性理论模型提出了采用修正的时域间断迦辽金有限元求解方法［9］。王颖泽等基于Lord-Shulman广义热弹性理论构建了热冲击下有限厚度圆柱壳的广义热弹性模型，并借助Laplace变换和Bessel函数的渐进特性研究了有界边界轴对称结构受热冲击的广义热弹性问题［10］。

在广义热弹性理论的研究中，少有人考虑材料的微结构特性。实际上，微结构存在于任何材料当中，尽管经典弹性理论得到了普遍接受和广泛应用，但由于经典理论的运动学描述只有应变张量表达的平动变形，不能反映材料微尺度力学效应等问题。而引入了旋转变形为发展弹性理论和弹性动力学注入了新的活力。经典的弹性理论认为应力只与应变或其应变历史有关，表现为一阶简单材料。而研究表明在某些情况应力还与其应变梯度有关，表现为二阶或高阶材料［11-13］。Voigt首先提出，在连续介质理论中微元体表面除了存在应力矢量外，还有存在应力偶矢量的可能性［11］。其后，Cosserat等扩展了此理论并推导了场方程［12］。Truesdell等在弹性理论前提下给出了准确的理论推导［13］。不同于经典连续介质理论，一些广义的连续介质理论考虑了微结构效应，可以更加有效地描述一些力学现象。偶应力弹性介质中引入了旋转变形，除了外部的平动变形应变张量还考虑了经典弹性介质所没有涉及到的偶应力张量，反映了材料的微尺度力的影响。不同于微极弹性理论，偶应力弹性理论对每个质量点只考虑其旋转自由度，且偶应力场合应力场相互解耦而不考虑额外的微转动矢量。其中，Toupin和Mindlin等建立并发展了偶应力理论，其中Toupin建立了完全弹性固体有限变形的本构关系［14］，而Mindlin扩展研究了均匀各向同性的中心对称弹性固体，建立了修正的边界条件［15］。Aero等推导了对应线性理论的应力平衡方程和本构关系［16］。对于线弹性偶应力介质，存在一个额外的材料参数称为转动参量。它与剪切模量比的平方根有长度的量纲，是重要的材料参数，体现了偶应力弹性介质和经典弹性介质的本质区别。此材料参数的量级通常小于材料尺度，然而其影响可能与材料尺度的影响相当。张敦福等采用偶应力理论和有限单元法，对含充填层状岩体结构面边界层效应进行了研究［17］。吴延峰等基于该理论建立平面应变问题的有限元计算模型，研究拉力型锚杆锚固段界面上的剪应力分布、界面附近的边界层效应和偶应力的尺度效应［18］。苏文政等基于偶应力理论对一类周期性多孔固体类梁结构给出了分析其横向自由振动的等效连续介质铁木辛柯梁模型，推导了等效铁木辛柯梁的动力学微分方程［19］。贺丹等基于修正偶应力理论建立了含有1个尺度参数的复合材料斜交铺设层合Kirchhoff板模型，给出了四边简支反对称角铺设微尺度层合Kirchhoff板的解析解［20］。

现有文献中对考虑Lord-Shulman广义热弹性理论的偶应力热弹性介质控制方程的推导过程鲜有提及。文章将基于Lord-Shulman广义热弹性理论，在热弹性介质中考虑偶应力张量的存在，从热力学定律出发系统地推导偶应力热弹性介质的基本方程和边界条件，并讨论Lord-Shulman理论对于偶应力热弹性介质控制方程的影响。

1　偶应力热弹性介质控制方程的推导过程

1.1偶应力介质的运动平衡方程和边界条件

均匀各向同性的偶应力弹性介质，不仅存在六面体单元三个面上的三个方向的应力σij，还存在六面体三个面上的三个方向的偶应力μij。在任意表面下，法线方向nj的应力可以写成ti=σjinj，力偶可以写成mi=μjinj。采用国际单位制，并且令字符上方的点表示对时间的导数，字符下标的逗号表示对坐标的导数。则动量平衡方程和动量矩平衡方程分别由式（1）、（2）表示为

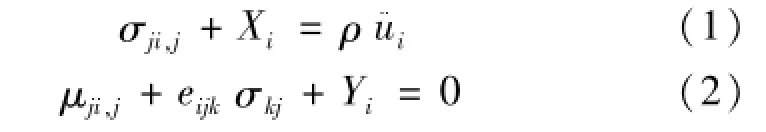
式中：σji，j为应力张量的散度，N/m3；Xi为外体力矢量，N/m3；ρ为质量密度，kg/m3；u¨i为位移矢量对时间的二次导数，m/s2；μji，j为偶应力张量的散度，N/ m2；eijk为笛卡尔坐标系下的Eddington张量；Yi为体力偶矢量，N/m2。

应力张量σij可以表示成对称部分和反对称部分的和，由式（3）表示为

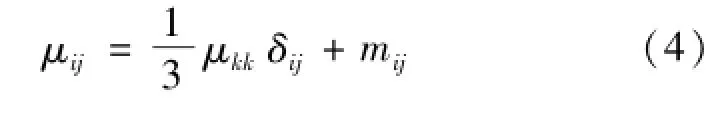
偶应力张量μij可以表示成球量张量和偏量张量的和，由式（4）表示为式中：δij为单位张量；mij为偶应力偏量张量，N/m，且mii=0。

式（2）两端同乘Eddington张量eimn，可以得到应力张量的反对称部分，由式（5）表示为

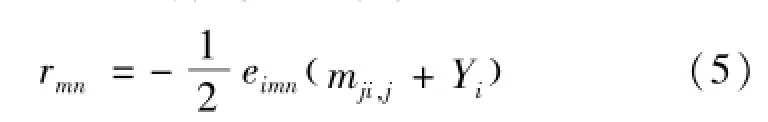
式中：rmn应力张量的反对称部分，N/m2；mji，j为偶应力偏量张量的散度，N/m2。

将式（3）～（5）代入式（1）中，可以得到式（6）为

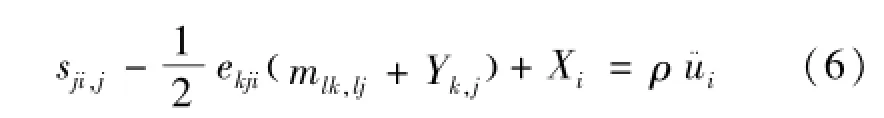
式（6）即为偶应力热弹性介质的运动平衡方程。

考虑能量守恒定律。对于介质的边界为A的任意体积V，忽略热源项，物体的动能和内能的增长率等于体力功率、面力功率和热量传入速率之和，由式（7）表示为

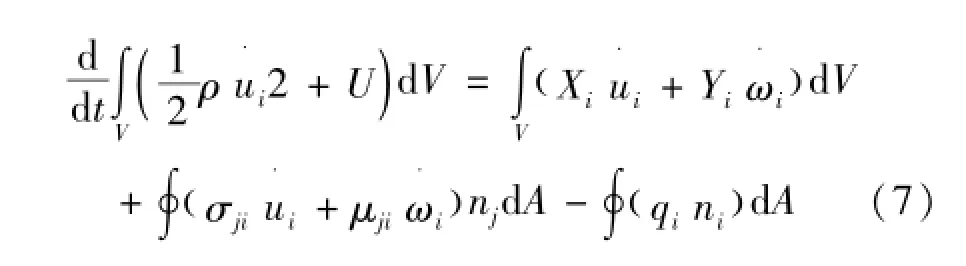
式中：U为内能，J/m3；ωi=eiklul，k/2为转动矢量；qi为热流矢量，J/（m2s）。

对于式（7）等号右边的第二项，分别由式（8）、（9）表示为式中：为转动矢量的时间导数，1/s；ni为方向矢量。

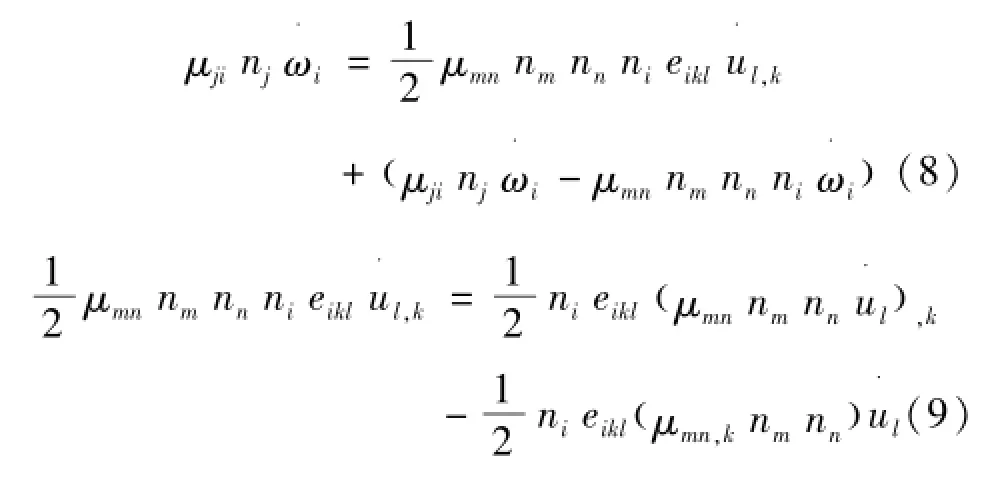
若物体表面光滑，则由式（10）表示为

因此在不考虑体力项和热流项时，式（7）可以由式（11）表示为

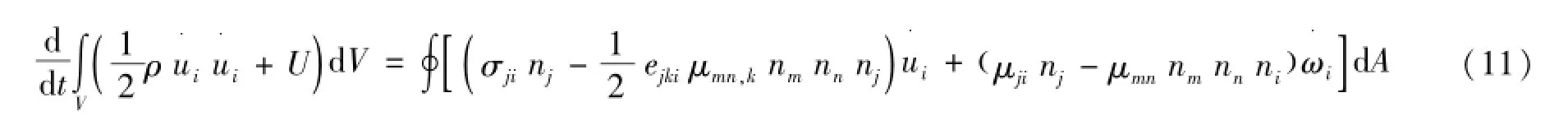
为了直观地描述边界条件的表达形式，设偶应力条件下修正应力和偶应力的切向分量分别由式（12）、（13）表示为

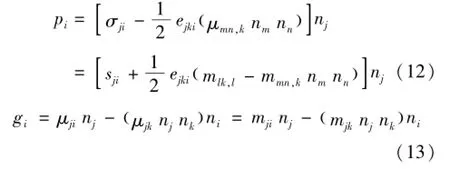
式中：pi为修正应力，N/m2；gi为偶应力的切向分量，N/m。

从式（12）、（13）可以看出，修正应力pi中既有应力张量部分，又包含了偶应力的法向分量。偶应力弹性介质的边界条件表达形式是与经典弹性介质所区别的地方之一。因此，式（11）可以写为式（14）

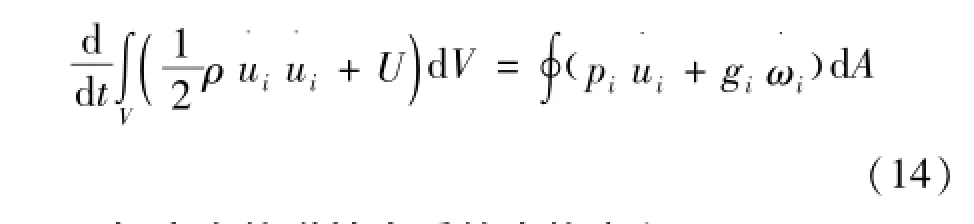
1.2偶应力热弹性介质的本构方程

对于能量守恒定律式（7），积分连续且对任意的体积V都成立，由散度定理可以得到式（15）为

式中：qi，i为热流的散度，J/（m3·s）。

考虑运动平衡方程式（1）、式（2）和边界条件式（12）、（13），可以得到式（16）为

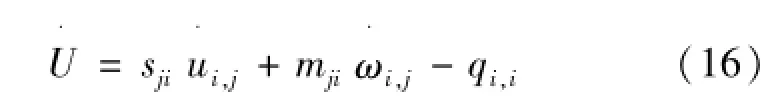
引入应变张量和扭转曲率张量，分别由式（17）、（18）表示为

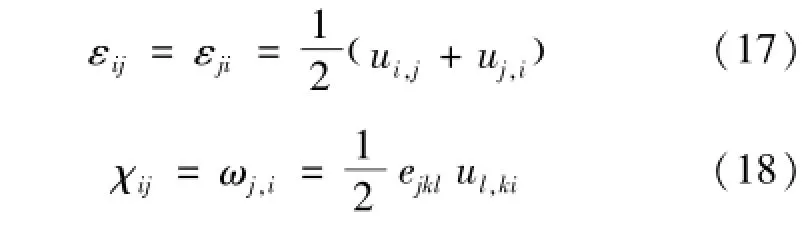
式中：εij为应变张量；χij为扭转曲率张量，1/m。因此，式（16）可以得到式（19）为

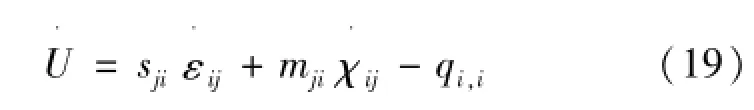
根据熵平衡定理，熵增率等于通过表面输送熵的流入率和通过热传导熵产率之和，由式（20）表示为

式中：S为熵密度，J/（m3·K）；Θ为熵流量，J/（m3·Ks）。

对式（20）利用散度定理，而且对任意的体积V都成立，由式（21）表示为

高速GPS和强震台网的另一个重要用途是提供近场地震波形数据，而这种数据对约束运动学震源过程有用。实际上，低频带的波形信息对反演震源时间函数特别有用。因此，我们需要通过强震记录得到速度或位移地震图，这对经验基线校正方法也是必要的。不进行基线校正，就需要对强震记录进行高通或者带通滤波，从而导致低频和静态地面形变信息的丢失，而这些信息对估计矩震级非常重要。

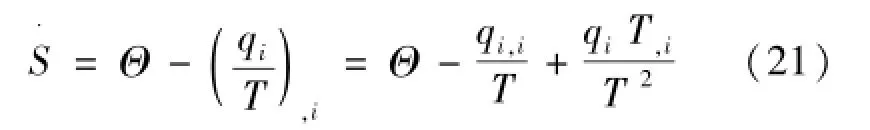
式中：T，i为温度梯度，K/m。

对每一个物质点都成立，而且与不可逆过程的热力学假设Θ≥0相一致。联立式（16）和式（19）可以得到式（22）为

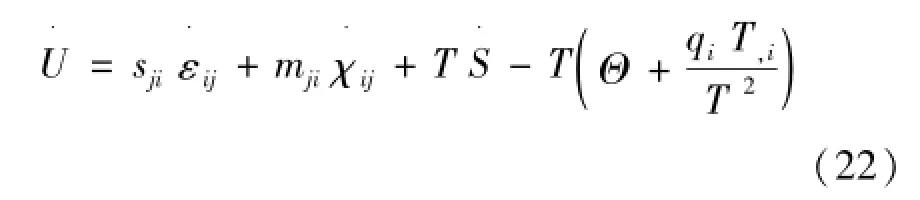
引入Helmholtz自由能函数，由式（23）表示为

式中：Φ为Helmholtz自由能函数，J/m3。

将式（23）代入式（21）可以得到Helmholtz自由能函数的时间导数，由式（24）表示为

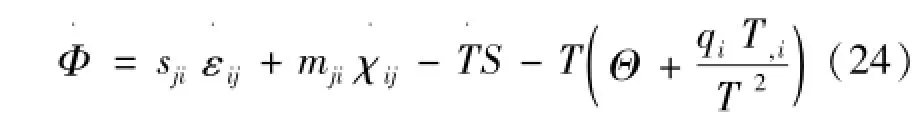
Helmholtz自由能函数是状态函数，可选取εij、 χij、T和T，i为独立变量，即可以得到式（25）为

若式（26）对任意的独立变量都成立，由式（27）表示为

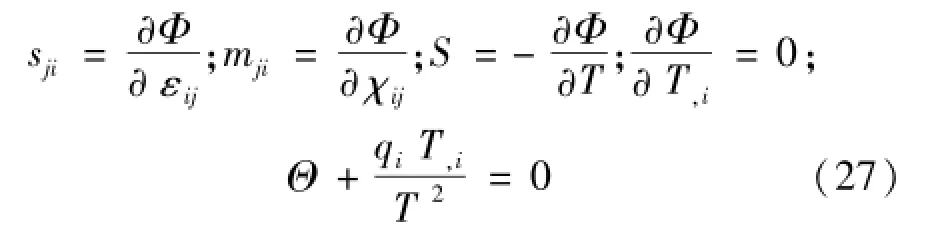
由式（27）可知，Helmholtz自由能函数与温度梯度T，i无关，其独立变量只有εij、χij和T，即Φ=。

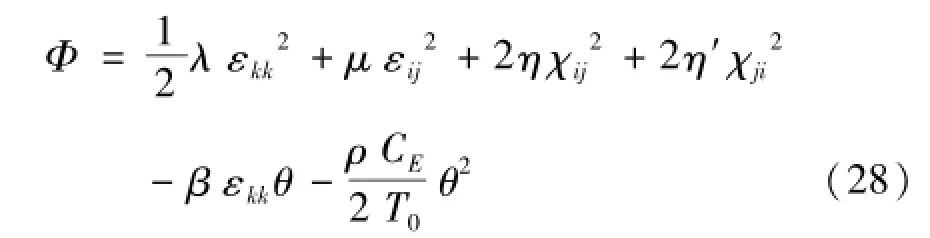
将式（28）代入式（27），可以得到式（29）～（31）为

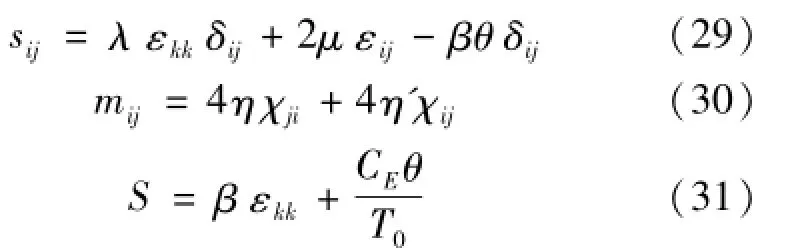
式（27）即为偶应力热弹性介质的本构方程，式（29）和（30）是有关机械量的本构方程，其中含有温度场的项；式（31）是有关热学量的本构方程，其中也含有机械场的项。可以看出，在考虑热弹性的影响时，偶应力介质中机械场与温度场相互耦合。

1.3基于Lord-Shulman理论的能量方程

当热力学假设Θ≥0成立时，式（27）满足热力学第二定律，由式（32）表示为

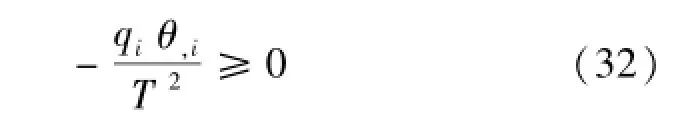
在均匀各向同性介质中，此不等式满足Fourier热传导定律，由式（33）表示为

式中：κ为热导率，J/（m·K·s）。式（33）是对热传导过程的一种简化表述，即Fourier热传导定律，忽略了热流的加速过程。考虑到热流加速而产生的弛豫时间，非Fourier热传导理论修正了热传导方程，考虑了热流率项，确保了热信号在介质中以有限的速度传播的特性，假设了一种热流qi和温度梯度θ，i更加广泛的关系式，由式（34）表示为

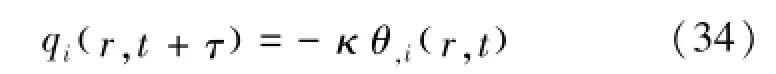
将式（34）左边一阶泰勒展开，可以得到式（35）为

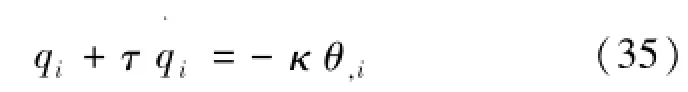
式中：τ为热流出现到温度梯度产生所需的弛豫时间，s。

由式（21）和（27），可以得到式（36）为将式（27）代入式（36），可以得到式（37）为

联立式（34）和（37），可以得到自由能形式的能量方程，由式（38）表示为

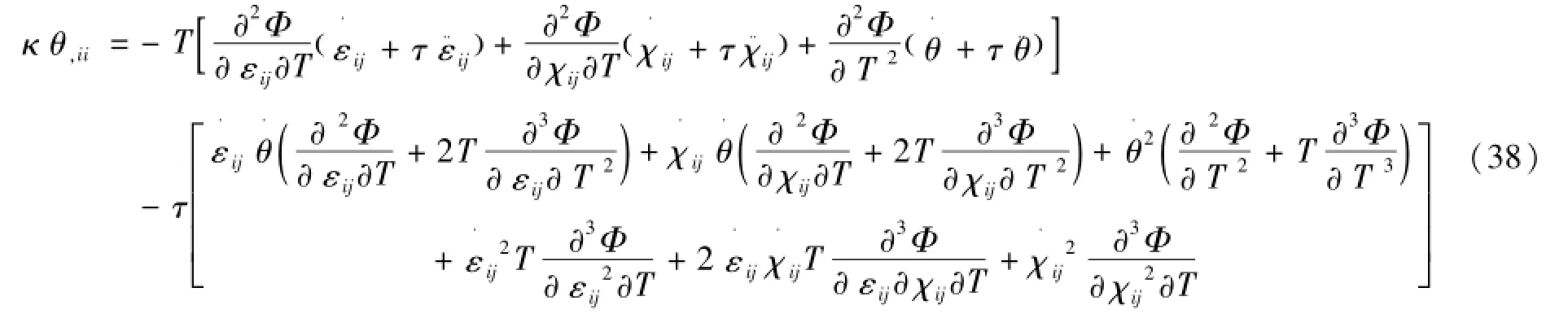
考虑线性理论假设，忽略式（38）等号右边的第二项，可以得到式（39）为

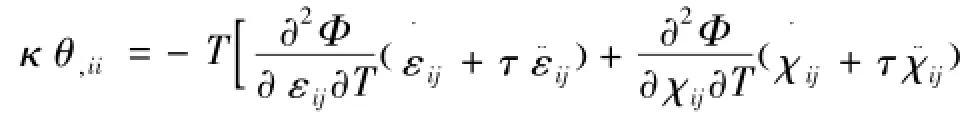
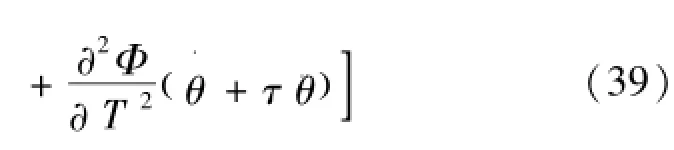
将式（28）代入式（39），可以得到式（40）为

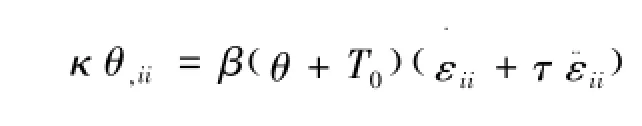
通常假设|θ/T0|≪1，能量方程可以化简为式（41）为

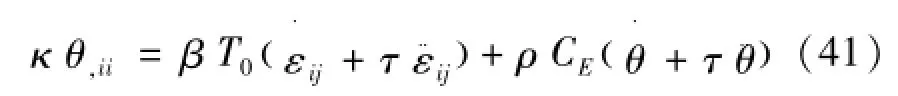
式（37）即为偶应力热弹性介质的能量方程。从中可以看出，方程中包含弛豫时间τ，是双曲型方程，这意味着热信号的传播是以波动的形式而不是扩散的形式，这是与经典热弹性理论下的偶应力介质能量方程所区别的地方。当τ超近于0时，能量方程退化抛物型方程，热信号的传播改为扩散的形式。

2　偶应力热弹性介质控制方程的导出

将本构方程式（29）～（31）代入运动平衡方程式（6）和能量方程式（41）中，可以得到偶应力热弹性介质的控制方程，分别由式（42）、（43）表示为

式（42）和（43）分别为偶应力热弹性介质的运动控制方程和温度控制方程。

以x方向为例，将控制方程以分量形式，分别由式（44）、（45）表示为

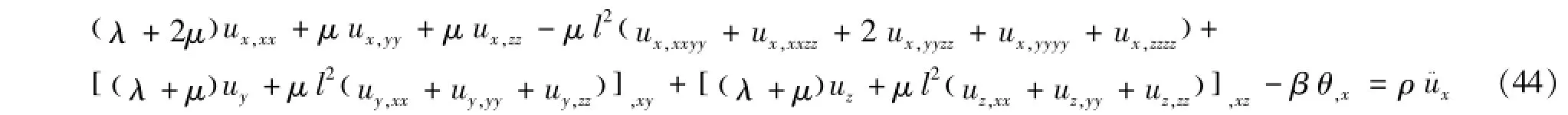
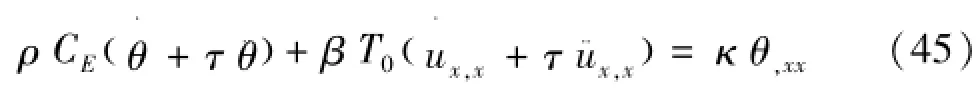
可以看出，与经典热弹性理论的控制方程相比，基于Lord-Shulman广义热弹性理论的偶应力热弹性介质的运动控制方程中含有偶应力特征参数l，温度控制方程中含有弛豫时间τ，分别体现了偶应力和非Fourier热传导对于热弹性介质的控制方程的影响。当运动控制方程中的参数l=0时，偶应力特征参数的影响消失，运动控制方程退化为经典热弹性理论的形式；温度控制方程中含有弛豫时间τ，是一个双曲型方程。由双曲型方程的性质，可以得到热信号的传播速度，由式（46）表示为

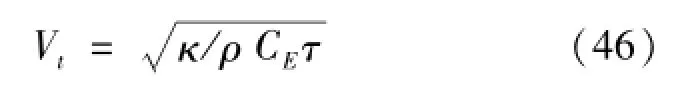
式中：Vt为热信号的传播速度，m/s。由于式（46）中热导率、质量密度和常应变下的比热均不为零，因此只有当弛豫时间τ=0时，热信号的传播速度才为无限大。这时温度控制方程由双曲型方程变为抛物型方程，退化为了经典热弹性理论形式，热信号也变成了扩散的形式，不再以波动的形式传播。

3　结论

通过上述研究可知：

（1）与经典热弹性理论控制方程相比，基于Lord-Shulman理论推导出的控制方程中机械场与温度场相互耦合，而且温度控制方程中含有弛豫时间项，使热信号以波动的形式和有限速度传播，体现了偶应力和非Fourier热传导的对于热弹性介质的控制方程的影响。

（2）当运动控制方程中的参数l=0时，偶应力的效应消失，运动控制方程退化为经典热弹性理论的形式；当温度控制方程中的弛豫时间τ=0时，温度控制方程变为抛物型方程，退化为经典热弹性理论的形式，而且热信号的传播也变成了扩散的形式。

［1］ 王洪钢.热弹性力学概论［M］.北京：清华大学出版社，1989.

［2］ Lord H.W.，Shulman Y..A generalized dynamical theory of thermoelasticity［J］.Journal of Mechanics Physical Solids，1967，15（5）：299-309.

［3］ Green A.E.Lindsay K.A..Thermoelasticity［J］.Journal of Elasticity，1972，2（1）：1-7.

［4］ Green A.E.，Naghdi P.M..A Re-Examination of the basic postulates of thermomechanics［J］.Proceedings of the Royal Society A Mathematical Physical&Engineering Sciences，1991，432（432）：171-194.

［5］ Chandrasekharaiah D.S..Thermoelasticity with second sound：a review［J］.Applied Mechanics Reviews，1986，39（3）：355-376.

［6］ Chandrasekharaiah D.S..Hyperbolic thermoelasticity：a review of recent literature［J］.Applied Mechanics Reviews，1998，51（12）：705-729.

［7］ 田晓耕，沈亚鹏.广义热弹性问题研究进展［J］.力学进展，2012，42（1）：18-28.

［8］ 任康乐，周凤玺，鲁庆华，等.功能梯度材料广义热弹性响应［J］.兰州理工大学学报，2012，38（2）：168-172.

［9］ 郭攀，武文华，吴志刚.非傅里叶热弹性的时域间断迦辽金有限元方法［J］.力学学报，2013，45（3）：447-450.

［10］王颖泽，王谦，刘栋，等.有限厚度圆柱壳热冲击问题的广义热弹性解［J］.应用数学和力学，2016，37（6）：644-654.

［11］Voigt W..Theoretische Studien Über Die Elasticitätsverhältnisse DerKrystalle［M］.Göttingen：KöniglicheGesellschaftder Wissenschaften zu，1887.

［12］Cosserat E.，Cosserat F..Théorie des corps déformables［J］. Nature，1909，81（2072）：242-246.

［13］Truesdell C.，Toupin R..The Classical Field Theories［M］. Berlin：Springer Berlin Heidelberg，1960.

［14］Toupin R.A..Elastic materials with couple-stresses［J］.Archive for Rational Mechanics and Analysis，1962，11（1）：385-414.

［15］Mindlin R.D.，Tiersten H.F..Effects of couple-stresses in linear elasticity［J］.Archive for Rational Mechanics and Analysis，1962， 11（1）：415-448.

［16］Aero E.L.，Kuvshinskii E.V..Fundamental equations of the theory of elastic media with rotationally interacting particles［J］. Soviet Physics-Solid State，1961，2（7）：1272-1281.

［17］张敦福，王相玉，李术才.偶应力对含充填层状岩体边界层效应的影响［J］.岩石力学与工程学报，2011（S1）：3288-3294.

［18］吴延峰，张敦福，张波，等.拉力型锚杆锚固界面剪应力分布偶应力理论分析［J］.岩土力学，2013，34（z1）：187-191，227.

［19］苏文政，刘书田.一类多孔固体的等效偶应力动力学梁模型［J］.力学学报，2016，48（1）：111-126.

［20］贺丹，杨万里.基于新修正偶应力理论的斜交铺设层合Kirchhoff板模型与尺度效应［J］.复合材料学报，2016，33（6）：1311-1317.

Derivation of governing equations of couple-stress thermoelastic medium

Li Long，Wei Peijun

（Department of Applied Mechanics，University of Science and Technology Beijing，Beijing 100083，China）

With the consideration of non-fourier heat conduction，the Lord-Shulman generalized thermoelastic theory contains a hyperbolic heat conduction equation，and the couple-stress is introduced to reflect the effect of microscale and the microstructural characteristics of materials.Based on the Lord-Shulman generalized thermoelastic theory，the article analyzes the derivation of the motion equations，the constitutive equations，the energy equations and the boundary conditions in the couplestress thermoelastic medium，obtaining the forms of motion governing equation and temperature governing equation.The results show that，compared with the governing equations of the classical theory，the ones based on Lord-Shulman theory in which the equations of the thermal field and the mechanical field are coupling with each other and the governing equations of temperature field contain the relaxation times item.So the propagation of thermal signal is in the form of fluctuation，and the velocity of it is finite，and the equations can also degenerate into the classical ones when letting the couple-stress constant and the relaxation time be zero.

couple-stress elasticity；Lord-Shulman theory；generalized thermoelasticity；non-fourier thermal conduction

O343.7

A

1673-7644（2016）04-0378-07

2016-08-01

李龙（1991-），男，硕士，助理工程师，主要从事弹性波理论等方面的的研究.E-mail：linkenzoo@163.com