基于穷举搜索法的地下岩土热物性参数分析

吴　迪，于明志，2*

（1.山东建筑大学热能工程学院，山东济南250101；2.山东建筑大学可再生能源建筑利用技术教育部重点实验室，山东济南250101）

基于穷举搜索法的地下岩土热物性参数分析

吴迪1，于明志1，2*

（1.山东建筑大学热能工程学院，山东济南250101；2.山东建筑大学可再生能源建筑利用技术教育部重点实验室，山东济南250101）

地下岩土热物性参数测量的准确性影响地埋管换热器设计的合理性，进而影响地源热泵系统初投资和运行性能。文章利用穷举搜索法结合参数估计方法对热物性参数组合值进行全域搜索，并获得地埋管循环水温度测量值与模型计算值之间的方差和最小值，通过模拟验证该方法计算结果的可靠性，并与优化方法计算结果对比分析。结果表明：穷举搜索法可以确定较为准确的热物性参数值；优化方法仅确定的导热系数具有可靠性，相对误差小于1%，但钻孔内热阻和容积比热计算结果相对误差可达到70%以上，可信度较差；在实际工程中，优化方法所得的导热系数的值与穷举搜索法所得的值接近，但钻孔内热阻相对偏差最高可达41.42%，相对应的容积比热相对偏差最高为67.98%。

岩土；热物性参数；穷举搜索法；优化方法

0　引言

地源热泵凭借其对环境污染小、使用寿命长、效能系数高等优势在近年来得到快速发展，地源热泵系统主要以浅层地表作为热源，利用地埋管中循环介质从其提取热量或向其释放热量，达到向室内提供热量或冷量的目的［1-2］。合理设计地埋管长度将直接影响到钻孔深度及个数，而地埋管设计的合理性与岩土热物性参数有着直接联系，另据Kavanaugh的研究显示，当地下土壤的导热系数或热扩散率发生10%的偏差时，地下埋管设计长度偏差为4.5%～5.8%，从而影响地源热泵系统初投资，所以，得到准确的岩土热物性参数值显得尤为重要［3-5］。国内外研究中提出的获取地下岩土热物性参数的主要方法有取样测试法和现场测试法，取样测试法是将现场取样后送至实验室进行测量，测量采用的模型主要有点热源模型［6］、线热源模型［7］和面热源模型［8］等。取样测试法存在的主要问题是由于水分散失等原因，导致试样与其原位状态相比可能发生一定变化。目前，国内外主要采用现场测试法。恒热流测试法是国际上普遍采用的获取地下岩土热物性参数值的现场测试方法，美国俄克拉何马州州立大学利用建立的大型沙箱实验平台，验证现场热物性测试可以得到较为准确的热物性参数值［9］。

恒热流测试法是在现场进行热响应实验，采用恒定功率加热地埋管循环水，循环水在埋管中循环流动并与周围岩土进行换热，根据测量得到埋管进出口位置循环水温度随时间的变化，得到从测试开始到热平衡过程中温度随时间的响应曲线。根据测试得到的数据结合地埋管与周围岩土传热模型进行计算，并利用参数估计法最终得到地下岩土的导热系数、容积比热等热物性参数值［10-11］。常用的传热模型有线热源模型［12］、空心柱热源模型［13］、实心柱热源模型［14］等，计算岩土热物性参数值通常采用斜率法［15］和参数估计法［16］。斜率法可以方便地得到岩土导热系数，但不能确定容积比热［17］；参数估计法可以同时确定导热系数、容积比热以及钻孔内热阻数值，在工程计算中被广泛应用［18-19］。参数估计法通常是利用最优化方法寻找根据模型计算得到的循环水温度与实验测量结果之间的方差和最小值，该目标函数方差和取得最小值时对应的岩土热物性数值即认为是测试得到的真实热物性参数值［20］。

利用优化方法可以快速得到符合要求的目标函数值，进而确定热物性参数值，但优化方法通常寻找到的是局部区域目标函数方差和极小值而不一定是全局区域最小值，且寻优结果受搜索初始值影响，这导致在具体实践中，输入的搜索初始值不同有可能导致得到不同岩土热物性参数值，从而影响地埋管换热器设计［21］。鉴于此，文中采用穷举搜索法，在岩土热物性参数值可能的范围内寻找目标函数方差和最小值，进而确定热物性参数［22］。

1　地埋管与周围岩土传热模型

由于线热源模型计算结果满足工程设计需求，且计算简单、适用性强［23］，所以文章采用的地埋管与周围岩土传热模型为目前广泛应用的线热源模型。线热源模型对地埋管及地下岩土进行了如下假设［24］：（1）大地视为无限大介质；（2）地埋管位于钻孔中心，并视为一根无限长的线热源；（3）地埋管周围回填材料及地下岩土均匀一致，且物性参数维持恒定；（4）钻孔内不考虑热量累积；（5）忽略岩土内的水分迁移、不同材质间的接触热阻。

基于上述假设，其控制方程，初始条件和边界条件由式（1）表示为

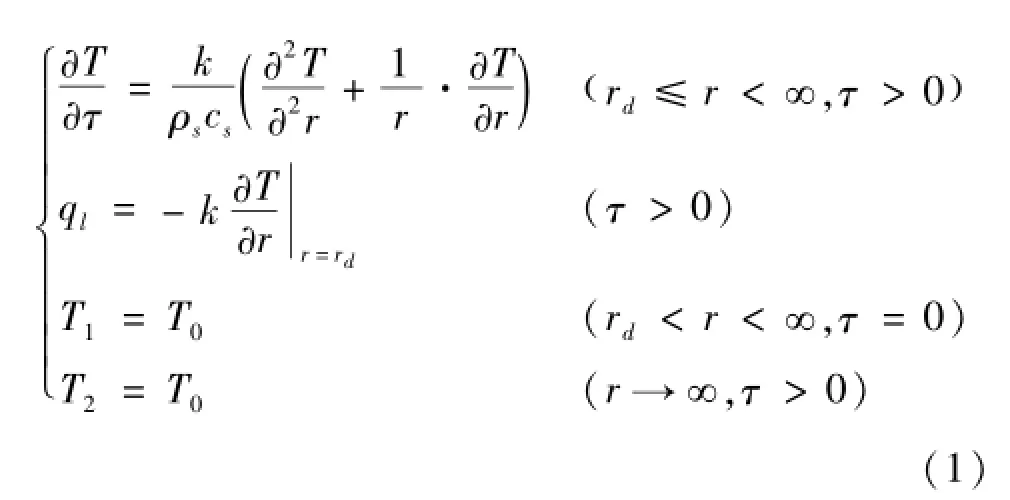
式中：T为τ时刻距离线热源中心r处的温度，℃；T0为土壤初始平均温度，℃；rd为钻孔半径，m；ql为埋管每延米换热量，W/m；ρscs为岩土容积比热，J/（m3·K）；k为岩土导热系数，W/（m·K）；τ为时间，s。

循环水平均温度Tcal与钻孔壁温Tw的关系式由式（2）表示为

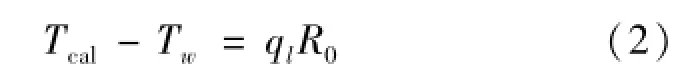
则循环水进出口平均温度Tcal［25］由式（3）表示为

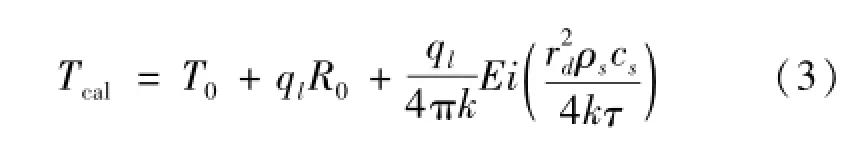
式中：R0为回填材料热阻，（m·K）/W；Ei（X）为指数积分函数，具体积分表达式由式（4）表示为

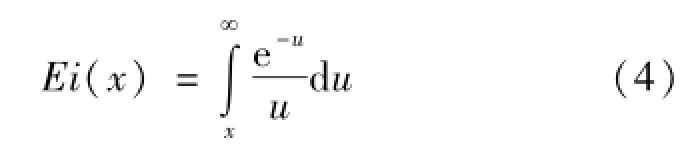
参数估计法目标函数为地下埋管与周围岩土传热模型计算得到的循环水平均温度与实际测量值之间的方差和［11］，由式（5）表示为

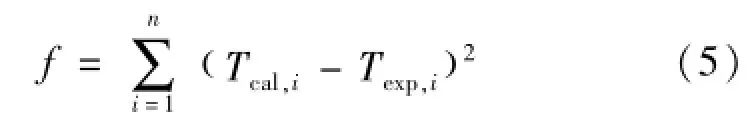
式中：Tcal，i为第i时刻由传热模型计算得到的地埋管内循环水平均温度，℃；Texp，i为第i时刻热响应实验测得的循环水平均温度，℃；n为数据测量组数。

2　地下岩土热物性参数估算主要方法

穷举搜索法是将岩土热物性参数可能取值范围内的不同数值组合带入到公式（3）中，得到循环水温度随时间变化的计算值，然后利用公式（5）计算循环水温度计算值与测量值之间的方差和，从中寻找到参数估计法目标函数方差和的最小值，此时对应的岩土热物性参数值即认为是所需测量的结果。

穷举搜索法将热物性参数的可能取值全部考虑在内，并逐一进行目标函数方差和的计算，比较得到方差和最小值。穷举搜索法与优化方法相比，优点是不受搜索初始值变化的影响，在给定的搜索域内，可得到唯一确定的目标函数方差和最小值，而不是某局部区域的极小值，从而确定其对应的物性参数。优化方法是通过研究优化途径及方案，最终寻找到局部最优解的方法，其计算速度快，可以快速寻找到符合要求的目标函数方差和及其对应的热物性参数值，但是找到的目标函数方差和一般是局部区域的极小值，而不是最小值，因此其结果可信度较穷举搜索法差，且优化方法受初始参数设定值的影响较大，计算结果不唯一。由于穷举搜索法要对全局范围内所有参数进行计算分析与比较，所以，穷举搜索法运算时间较优化方法长。

3　地下岩土热物性参数验证与分析

3.1地下岩土热物性参数估算模拟验证与分析

为了验证穷举搜索法计算结果的准确性，预先设定钻孔直径D、每延米换热量ql、岩土导热系数k、钻孔内热阻R0、岩土容积比热ρscs等参数值，并用以计算循环水温度值作为模拟的测量结果，然后利用穷举搜索法确定岩土热物性参数，将设定值与运算值进行对比分析。

采用两组参数设定值（见表1）分别进行验证。考虑到缩短搜索时间以及可能的岩土热物性参数值范围，文中选择的各参数搜索范围为0.4＜k＜6、0.005＜R0＜0.3和0.5＜ρscs＜6［26］。利用穷举搜索法的计算结果见表2，作为对比，同时采用复形调优法寻找目标函数方差和最优解，复型调优法适用于求解多变量最值问题，不需要求解目标函数偏导数，鲁棒性好，其结果见表3。为进一步验证两种计算方法结果的可信度，将模拟测试温度曲线与两种方法得到的计算温度曲线进行了对比，如图1、2所示。

由表2和3可知，穷举搜索法得到每组目标函数方差和均为0，即可以寻找到目标函数最小值，其对应的各参数值与设定值之间的相对误差也均为0，说明利用穷举搜索法可以准确地找到热物性参数值。而优化方法得到的结果与设定值之间存在一定误差，而且搜索初始值不同，得到的结果也不同。优化方法得到的导热系数受搜索初始值影响较小，而且与设定值之间的误差也不大，均在1%以内，目标方差和均小于1，但钻孔内热阻与容积比热受到搜索初始值的显著影响，而且较设定值误差偏大，可达到70%以上，最高分别为73.75%与81.67%。显然优化方法得到的导热系数准确度较高，但得到的钻孔内热阻和容积比热则可信度较差。如图1、2所示，两种方法的计算温度曲线对模拟测试温度曲线拟合均非常好。虽然优化方法在不同初始搜索值时得到的热物性参数不同，但其计算温度曲线与模拟测试曲线都几乎重合，由此可见计算温度曲线和测试温度曲线拟合良好并不能表明测试结果一定可靠。

表1　设定参数

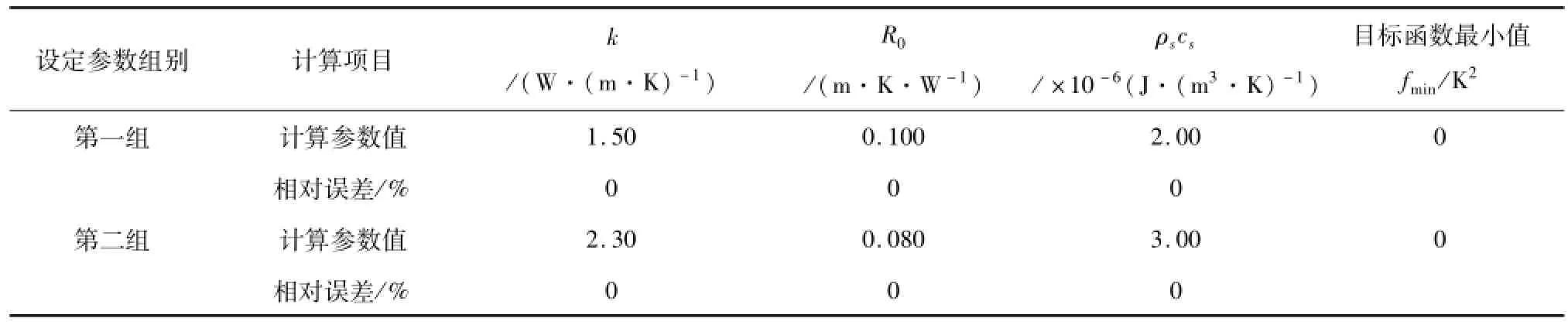
表2　穷举搜索法得到的岩土热物性参数

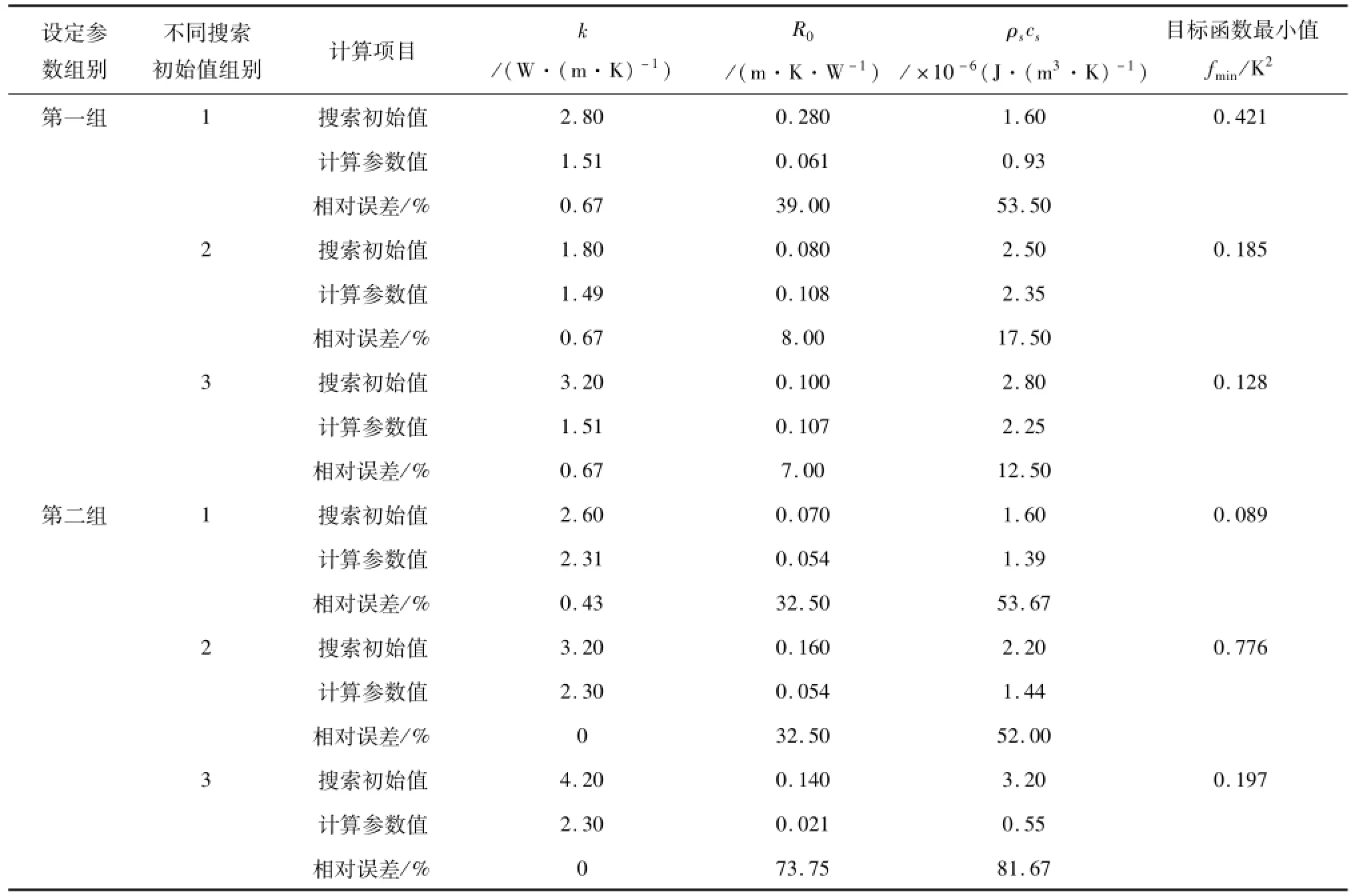
表3　优化方法得到的岩土热物性参数

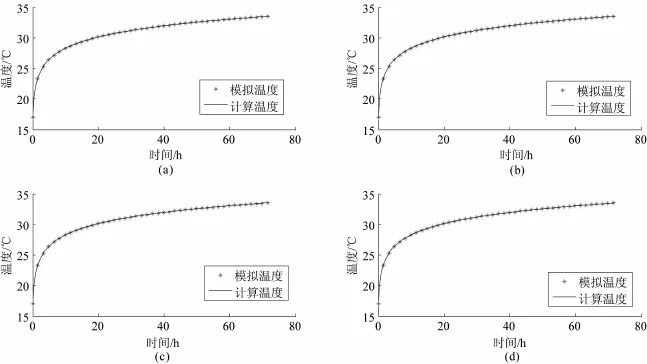
图1　第一组循环水温度随时间变化曲线图

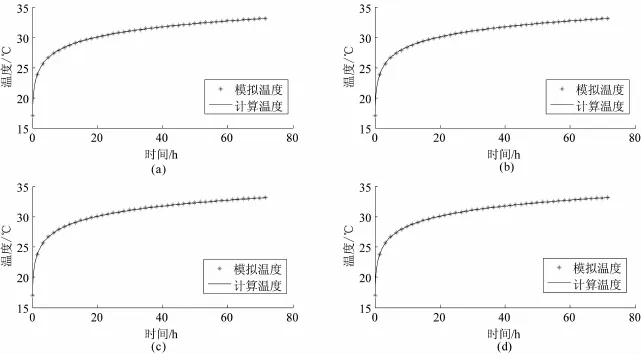
图2　第二组循环水温度随时间变化曲线图

穷举搜索法可以得到唯一一组热物性参数值，且目标函数方差和最小，计算温度曲线对模拟测试温度曲线拟合非常好，而优化方法却能找到多组不同的热物性参数值，显然穷举搜索法得到的热物性参数值与优化方法得到结果相比具有更高的可信度。

3.2实际工程应用案例分析

利用穷举搜索法分别对上海市（工程1）和青岛市（工程2）的两个工程项目进行了地下岩土热物性参数测量计算，实际测试工况见表4。现场测试得到的进出口循环水温度随时间的变化见图3、4中的实际测试温度曲线。另外，文中还采用优化方法对地下岩土热物性参数进行了计算，两种方法得到的结果见表5，两种方法利用岩土热物性参数计算得到的循环水温度见图3、4中的计算温度曲线。

表4　实际工程有关参数

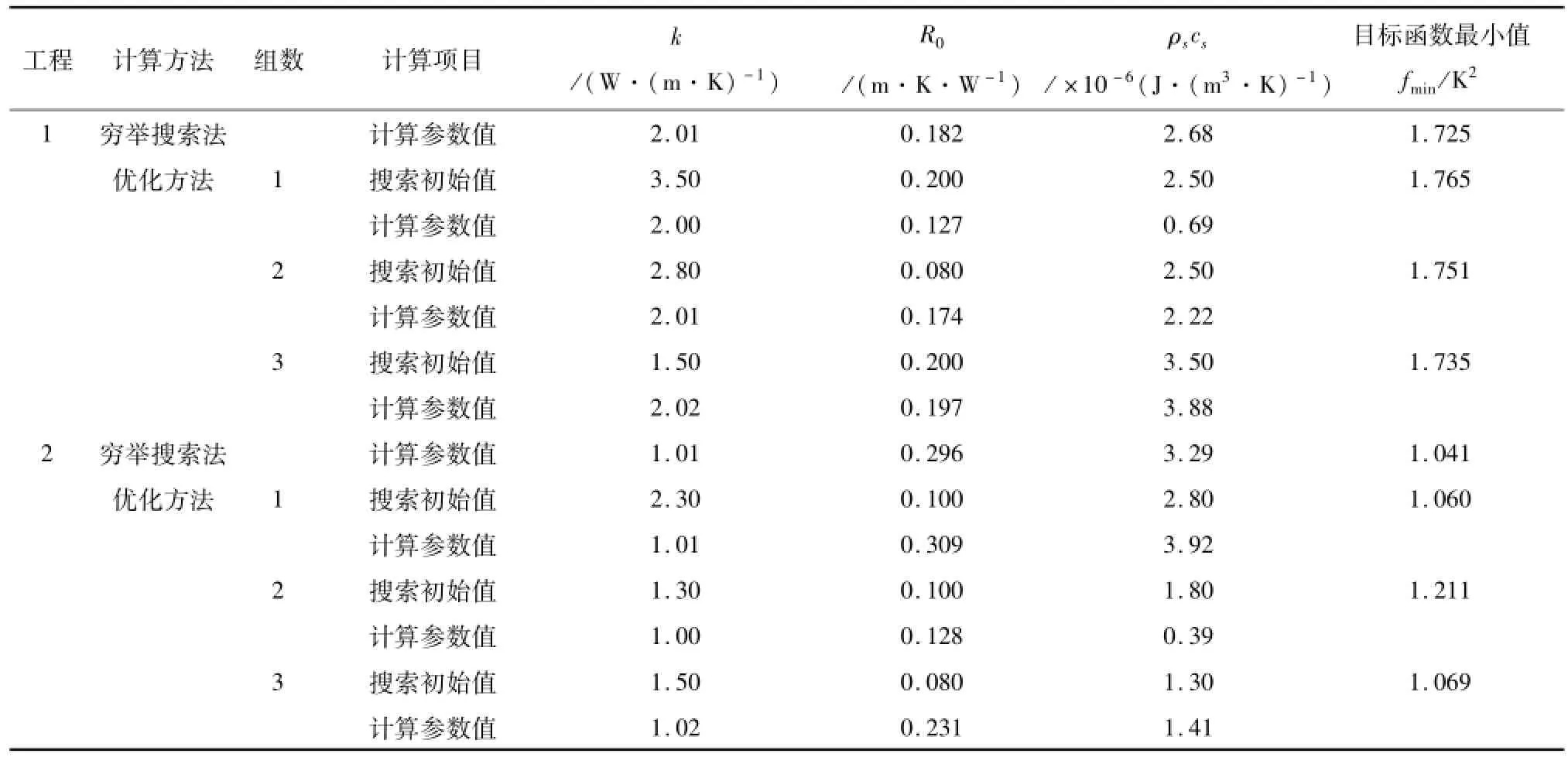
表5　穷举搜索法与优化方法得到的岩土热物性参数

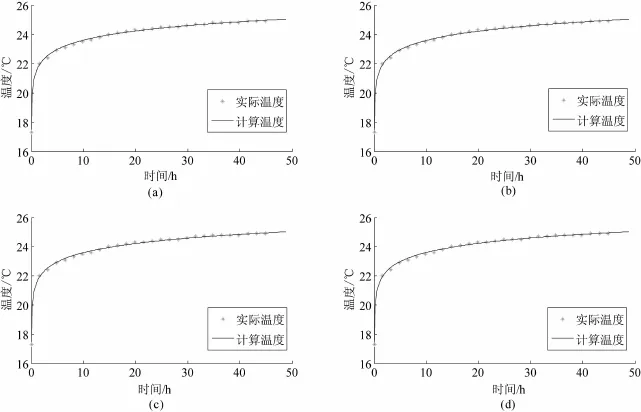
图3　工程1的循环水温度随时间变化曲线图

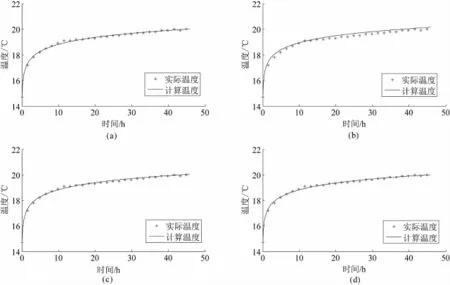
图4　工程2的循环水温度随时间变化曲线图

两种方法得到的导热系数值相对一致，不同搜索初始值时，优化方法得到的导热系数变化也不大，数值分别稳定在2.00～2.02 W/（m·K）、1.00～1.02 W/（m·K）之间，与穷举搜索法得到2.01 W/（m·K）、1.01 W/（m·K）基本吻合。工程1中地下土壤主要为含湿率较高的粘土、粉土，夹杂有粉砂、中粗砂；工程2中地下土壤主要由碎石构成，夹杂有粘土。粉砂岩的导热系数为0.8～4.0 W/（m·K），粘土岩的导热系数为1.8～3.0 W/（m·K）［7］，可以断定上述得到的工程1土壤导热系数可信性较高；碎石的导热系数为0.5～1.5 W/（m·K），所以对工程2的计算结果也在上述范围内，同样具有可信性。

优化方法得到的钻孔内热阻和容积比热受搜索初始值影响较大，工程1和工程2得到的钻孔内热阻最大值与最小值相对偏差可达21.60%和41.42%，容积比热最大值与最小值相对偏差分别为56.74%和67.98%。上述相对偏差显示，优化方法得到的钻孔内热阻、容积比热可靠性较差。此外，两个工程中穷举搜索法得到目标函数方差和最小值比优化算法得到的目标函数方差和极小值均要小。如图3、4所示，穷举搜索法得到的循环水计算温度曲线对实际测试温度曲线拟合较好。显然，穷举搜索法得到的热物性参数值具有较高的可信性。

由于优化方法得到的岩土导热系数受搜索初始值影响很小，而且计算速度快，如果只需要测量地下岩土导热系数，可采用优化方法。但如果还需确定容积比热或钻孔内热阻，由于优化方法的上述两参数计算结果对搜索初始值存在较大依赖性且相对偏差较大，因此在使用该方法时，要求使用者能对被测地点地下岩土热物性参数，特别是容积比热和钻孔内热阻，有较为接近实际值的估计，否则将很难得到较为真实的计算结果。而实际上，设计人员很难对地下岩土热物性作出接近实际值的估计，因此优化方法得到的地下岩土容积比热或钻孔内热阻可靠性很难保证。而穷举搜索法不存在搜索初始值的影响，仅得到唯一确定的热物性参数值，所以其结果更具可靠性。

4　结论

通过上述研究可知：

（1）穷举搜索法可以得到目标函数方差和最小值，进而确定准确唯一的热物性参数值，不受搜索初始值的影响，其得到的计算温度曲线对实际测试温度曲线拟合较好，计算结果具有较高的可信性。优化方法仅得到目标函数方差和极小值，其得到的岩土导热系数较为接近预设值，相对误差均小于1%，但钻孔内热阻及容积比热的结果与预设值相差较大，相对误差可达到70%以上，且各参数值随搜索初始值的不同而发生较大变化，结果可靠性较差。

（2）在工程1和工程2的热物性参数计算中，优化方法得到的导热系数值在2.00～2.02 W/（m·K）、1.00～1.02 W/（m·K）之间，与穷举搜索法得到2.01 W/（m·K）、1.01 W/（m·K）接近，可靠性较高，但钻孔内热阻最大值与最小值相对偏差可达21.60%和41.42%，相对应的容积比热相对偏差为56.74%和67.98%。显然，穷举搜索法得到的热物性参数值具有较高的可信性。

［1］ 刁乃仁，方肇洪.地埋管地源热泵技术［M］.北京：高等教育出版社，2006.

［2］ 刘明众.地源热泵特性分析及可行性研究［D］.淮南：安徽理工大学，2015.

［3］ Kavanaugh S.P..Field tests for ground thermal properties-methods and impact on ground-source heat pump design［J］.Ashrae Transactions，1998，104（2）：347-355.

［4］ 王沣浩，颜亮，冯琛琛，等.地源热泵岩土导热系数测试影响因素分析［J］.制冷学报，2012，33（4）：16-22.

［5］ 胡平放，孙启明，雷飞，等.岩土热物性测试若干问题探讨［J］.制冷与空调，2012，12（4）：109-111，94.

［6］ Alonso S.T.，Rey-Ronco M.A.，Carnero-Rodriguez F..Determining ground thermal properties using logs and thermal drill cutting analysis. First relationship with thermal response test in principality of Asturias，Spain［J］.Applied Thermal Engineering，2012（37）：226-234.

［7］ 杨文兵，丁云飞，官玲俊.热探针法测定含湿土壤的导热系数［J］.制冷空调与电力机械，2010，31（3）：13-15.

［8］ Gustavsson M.，Karawacki E.，Gustafsson S.E..Thermal conductivity，thermal diffusivity，and specific heat of thin samples from transient measurements withhotdisksensors［J］.ReviewofScientific Instruments，1994，65（12）：3856-3859.

［9］ Beier R.A.，Smith M.D.，Spitler J.D..Reference data sets for vertical borehole ground heat exchanger models and thermal response test analysis［J］.Geothermics，2011，40（1）：79-85.

［10］International Ground Source Heat Pump Association.Closed-Loop/ Geothermal Heat Pump Systems-Design and Installation Standards［M］.Oklahoma：Oklahoma State University，2007.

［11］Austin W.A..Development of an in situ system for measuring ground thermalproperties［D］.Oklahoma：OklahomaState University，1998.

［12］Ingersoll L.R.，Plass H.J..Theory of the ground pipe heat source for the heat pump［J］.ASHVE Transactions，1948，47（7）：339-348.

［13］Carslaw H.S.，Jaeger J.C.，Feshbach H..Conduction of heat in solids［J］.Physics Today，1962，15：74-75.

［14］于晓菲，于明志，张磊，等.基于实心圆柱面热源模型的岩土热物性测试方法［J］.化工学报，2012，63（S1）：84-87.

［15］Alonso-Sanchez T.，Rey-Ronco M.A.，Carnero-Rodriguez F.. Determining ground thermal properties using logs and thermal drill cutting analysis.First relationship with thermal response test in principality of Asturias，Spain［J］.Applied Thermal Engineering，2012（37）：226-234.

［16］艾克霍夫.系统辨识──状态与系统参数估计［M］.北京：科学出版社，1980.

［17］赵飞.现场岩土热响应测试及数据处理分析方法研究［D］.西安：西安建筑科技大学，2013.

［18］廖了，黄光勤，陈余量.岩土热物性参数的估算方法比选［J］.煤气与热力，2013，33（10）：1-3，7.

［19］Li M.，Lai A.C..Parameter estimation of in-situ thermal response tests for borehole ground heat exchangers［J］.Internation Journal of Heat and Mass Transfer，2012，55（9/10）：2615-2624.

［20］Pisello A.L.，Bobker M.，Cotana F..A building energy efficiency optimization method by evaluating the effective thermal zones occupancy［J］.Energies，2012，5（12）：5257-5278.

［21］Rose K.，Gurewitz E.，Fox G.C..Constrained clustering as an optimization method［J］.IEEE Transactions Pattern Analysis and Machine Intelligence，1993，15（8）：785-794.

［22］Engle J.A.，Legault K.R.，Rosati J.D..Sediment budget formulation via exhaustive search method［J］.Coastal Engineering Proceedings，2012，1（33）：121.

［23］Li M.，Lai A.C..Review of analytical models for heat transfer by vertical ground heat exchangers（GHEs）：A perspective of time and space scales［J］.Applied Energy，2015，（151）：178-191.

［24］张景欣，彭冬根，魏昊然，等.基于线热源模型的垂直U型埋管换热器的换热分析［J］.流体机械，2015，43（4）：75-79.

［25］Roth P.，Georgiev A.，Busso A.，et al.First in situ determination of ground and borehole thermal properties in Latin America［J］. Renewable Energy，2004，29（12）：1947-1963.

［26］肖衡林，吴雪洁，周锦华.岩土材料导热系数计算研究［J］.路基工程，2007（3）：54-56.

Exhaustive search method to determine the underground soil thermal properties

Wu Di1，Yu Mingzhi1，2*

（1.School of Thermal Engineering，Shandong Jianzhu University，Jinan 250101，China；2.Key Laboratory of Renewable Energy Utilization Technology in Building，Ministry of Education，Jinan 250101，China）

The accuracy of measured underground soil thermal properties affects the designing rationality ofground heat exchangers and then influences the investment and operation performance of the ground source heat pump systems.Together with the parameter estimation method，the exhaustive search method is used to determine the underground soil thermal properties by thoroughly searching the combinations of different soil thermal properties.The minimum variance between the measured and calculated circulating water temperature is to be obtained.However，the soil thermal parameters corresponds to the minimum variance are the results.After verifying the reliability verification of the exhaustive search method by simulation，the results are compared with those obtained by the optimization method.The result demonstrate that the exhaustive search method can obtain the more accurate group of soil thermal parameters.As comparison，though the optimization method can find the underground thermal conductivity with high credibility，the borehole thermal resistance and volumetric heat capacity are poor credibility.The relative error of underground thermal conductivity is less than 1%，but that of the borehole thermal resistance and volumetric heat capacity are more than70%.The results of thermal conductivity calculated by the optimization method range respectively from 2.00 to 2.02 W/（m·K）and from 1.00 to 1.02 W/（m·K）in these two projects.These results are close to the corresponding results of the exhaustive search method，2.01 W/（m·K）and 1.01 W/（m·K）.However，the borehole thermal resistance's highest relative deviation can be up to 41.42%.And corresponding volumetric heat capacity's highest relative deviation can reach 67.98%.

soil；thermal properties；exhaustive search method；optimization method

TU201.5

A

1673-7644（2016）04-0358-08

2016-05-18

国家自然科学基金项目（51176104）

吴迪（1991-），男，在读硕士，主要从事新能源与节能技术等方面的研究.E-mail：wudisjd@sina.com

*：于明志（1970-），男，教授，博士，主要从事传热传质、能源利用及节能等方面的研究.E-mail：yumingzhiwh@163.com