四边支承贴膜玻璃受弯承载性能分析

万成龙，卢　佳，孙诗兵，王洪涛

（1.北京工业大学材料科学与工程学院，北京100124；2.3M中国有限公司，北京100004；3.中国建筑科学研究院，北京100013）

四边支承贴膜玻璃受弯承载性能分析

万成龙1，3，卢佳2，孙诗兵1*，王洪涛3

（1.北京工业大学材料科学与工程学院，北京100124；2.3M中国有限公司，北京100004；3.中国建筑科学研究院，北京100013）

贴膜是防止非安全玻璃或钢化玻璃破裂后瞬时脱落的手段之一，为及时安全隔离并为维修提供时间，贴膜玻璃受弯承载性能研究对于贴膜玻璃的工程应用具有重要指导意义。文章基于有限元模拟计算和抗风压试验测试分析对四边支承贴膜玻璃受弯承载性能进行了分析。结果表明：膜层厚度不同时，玻璃贴膜前后挠度减小不明显，而贴膜后玻璃第一主应力减小约50%；在1、2、3和4 kPa均布风荷载作用下，挠度随着荷载值增加近似成线性变化，贴膜面正压挠度变形比负压挠度变形略大；挠度与均布荷载值呈近似线性趋势，随着均布荷载值增加，挠度测试值呈“先大于计算值，后小于计算值”的趋势，说明了模拟计算结果更为保守，修正后的模拟值与测试值更为接近。

四边支承；贴膜玻璃；受弯承载

0　引言

钢化玻璃在建筑门窗幕墙领域应用十分广泛，但钢化玻璃自爆以其突发性和脱落的不确定性成为钢化玻璃工程应用领域的难题。针对钢化玻璃自爆问题，除采用使用优质原片、进行均质处理等手段降低钢化玻璃自爆率外，还应在工程现场采取适当的防护隔离措施以确保人身财产安全，如采取绿化隔离带、雨棚等形式，在钢化玻璃自爆脱落时以最大限度降低损失。近年来，通过贴膜方式将自爆后的钢化玻璃整体保持在门窗幕墙框架上，从而及时更换处理，这方面研究已成为热点方向之一。

贴膜玻璃由玻璃与膜层连接成一个组合式结构，膜层一般为PET基材。基材为复合金属镀膜层，表面涂有耐磨层，背面涂有安装胶和外加的防粘保护膜，从而构成一种复合薄膜材料。

目前，建筑玻璃贴膜工程的研究主要集中在节能效果方面，而安全改造方面研究较少。龙文志对建筑玻璃贴膜的分类、膜材的选用、建筑玻璃贴膜的技术要点以及从工程应用角度对建筑玻璃贴膜相关标准进行了系统解读［1］；贺勇等对贴膜玻璃整窗的抗风压性能和保温性能进行了测试研究［2］；曹毅然等通过理论分析和实验研究得到玻璃系统的镀（贴）膜位置和热工参数之间的关系［3］；田学春等从贴膜种类、生产厂家、技术标准及施工要点等角度研究了玻璃贴膜在建筑节能中的应用［4］；高嘉明等通过对比实验室检测的贴不同隔热膜玻璃的特性参数，分析给出了可行而准确的玻璃贴膜节能效果的定量评估方法［5］；吴永昌等系统研究了建筑玻璃贴膜光学与热工性能，系统研究了贴膜产品的定义、构造、分类和分级，对比分析了贴膜玻璃与普通玻璃光谱的区别［6］；谢海容从理论上研究了贴膜玻璃窗的热传导模型、简化计算公式和传递到室内总热量的计算方法，现场实验测试表明太阳控制膜对太阳辐射强、空调时间比采暖时间长的地区的建筑有明显的节能效果［7］；楚洪亮等研究了普通玻璃窗和贴膜隔热玻璃窗在我国夏热冬冷地区和夏热冬暖地区典型城市的建筑节能效果［8］。

在安全改造方面，任鹏等对多组不同类型的贴膜玻璃试件进行了冲击试验，表明贴膜能够有效提高玻璃抗冲击能力且能有效避免玻璃受冲击后玻璃碎片的飞溅［9］；万成龙等首次提出了贴膜玻璃破碎后的安全性能指标——残余抗风压性能，研究了贴膜玻璃的残余抗风压性能，证明了边部构造合理的贴膜钢化玻璃在破碎后能承受比未贴膜钢化玻璃破碎后高的多的风压［10］；建筑玻璃贴膜应用技术规程提出了安全贴膜的最小厚度、贴膜与建筑支承构件的连接构造、外贴膜玻璃残余抗风压强度试验，对贴膜玻璃的施工工艺、验收和使用维护进行了规定［11］。

综上所述，贴膜玻璃的节能效果研究较为深入，而相关安全应用研究缺乏，仅有对贴膜玻璃的抗冲击性能、残余抗风压性能及边部构造的研究，缺乏贴膜对玻璃强度和刚度影响的研究。贴膜后玻璃表面受到贴膜材料的影响，尤其是贴膜面玻璃表面受到张拉力时，膜层的张拉力与玻璃本身的张拉力叠加，对玻璃的刚度和强度会产生一定的影响。

文章以贴膜对玻璃的受弯承载性能为研究对象，通过有限元模拟计算和风压加载试验的方法研究贴膜前后玻璃的强度和刚度变化，以明确贴膜对玻璃受弯承载性能的影响。研究对于节能改造和安全改造时贴膜玻璃的结构设计具有重要意义。

1　四边支承贴膜玻璃受弯承载性能研究方法

贴膜玻璃受弯承载性能主要研究贴膜对玻璃强度和刚度的影响。强度通过贴膜前后玻璃第一主应力的变化来反映，而刚度则是通过贴膜前后玻璃挠度变化来研究的。研究方法分为有限元模拟研究和试验分析研究，有限元模拟采用相应软件进行，试验分析采用静压箱法模拟均布风荷载的方法进行。

1.1有限元模拟

建筑工程中典型温度下玻璃特征是完全弹性的，玻璃通常不具有蠕变和松弛弹性。当玻璃面板变形较小时，可采用小变形理论计算外荷载作用下的玻璃面板内力和位移。大面积玻璃面板的实际位移一般要大于小变形理论所得结果，这是因为板弯曲变形会产生中面的拉应力，而小变形理论忽略了中面拉应力对位移和应力的阻止或抵消效应。所以对幕墙的玻璃面板，应采用精确的几何非线性方法进行分析和计算。

文章针对6 mm厚的玻璃，计算其在贴膜前后不同压力下的第一主应力变化和挠度，从而得到膜层对玻璃强度和刚度的作用。有限元计算结果内容较多，但用于工程分析一般取最大变形、最大应力或应变、支反力或力矩等，其中最大应力或应变应根据强度理论取值。玻璃为脆性材料，则应根据第一、第二强度理论，取最大主应力进行作为第一主应力［12-14］分析。

模拟用玻璃尺寸与实际测试板块同，为1930 mm×864 mm。贴膜基材为PET，膜厚分别为0.05、0.1和0.15 mm。贴膜玻璃是由一层贴膜和一层玻璃组成的复合结构。对于复合结构，ANSYS可以采用shell单元和solid单元来模拟。但shell单元无法考虑贴膜在层内相对滑移，计算值较实际偏小［15-19］。因此，膜片、玻璃的建模采用solid 45三维实体单元，该三维实体单元是8节点6面体单元，详细构造如图1所示。膜层和玻璃层为相同的实体单元，接触面采用共用节点连接。

图1　SOLID45单元图

在有限元分析时，对于工程中常用的四边支承玻璃面板（边长约为1000～3000 mm），每边划分出20～60个单元可保证精度；由于文章重点研究膜片对整个贴膜玻璃性能的影响，在实际划分网格时，需要在玻璃、膜片厚度的方向划分3个以上的网格，以满足计算需要［15-19］。玻璃及贴膜材料的力学性能参数见表1［20-22］。

表1　玻璃及贴膜材料力学性能参数

计算采用四边简支玻璃面板，为尽可能符合四边支承状态的约束情况，在左竖短边施加x、z向平动约束，在下长边施加y、z向平动约束，在其余两边施加z向平动约束，如图2所示［23］。在玻璃表面分别施加1、2、3、4、5 kPa均布荷载。同时，对未贴膜时的玻璃面板按类似处理计算。

图2　四边支承玻璃面板约束施加示意图

1.2抗风压试验

玻璃的抗风压试验，是通过测试玻璃面板在达到允许的最大相对面法线挠度时的风压值，从而确定玻璃板块的抗风压能力。相对面法线挠度是面法线挠度与两端测点间距离的比值，有框幕墙玻璃面板最大允许相对面法线挠度为玻璃面板短边边长的1/60。贴膜玻璃抗风压试验采用建筑幕墙门窗抗风压性能检测设备进行，其主要组成为压力箱、供压系统、测量系统及试件安装系统组成，贴膜玻璃抗风压试验装置如图3所示。

贴膜玻璃抗风压性能试验应分别进行正压和负压试验。正压和负压分别反映不同风向对幕墙的作用，正压反映幕墙门窗玻璃板块承受室外侧迎风面水平作用的风压力，负压反映幕墙门窗玻璃板块承受室外侧背风面水平作用的风吸力。对贴膜玻璃而言，贴膜面承受正压时玻璃向未贴膜一侧弯曲，未贴膜一侧承受表面张拉力，贴膜一侧承受表面压力；贴膜玻璃承受负压时，贴膜玻璃受力刚好相反，即未贴膜一侧承受表面压力，贴膜一侧承受表面张拉力。正负压加载示意如图4所示。可知，正压时未贴膜面表面仅承受玻璃本身弯曲带来的张拉力，由该张拉力抵抗正风压；负压时贴膜面除承受玻璃本身因负风压带来的张拉力外，还承受贴膜带来的表面张拉力。

图3　贴膜玻璃抗风压试验装置图

图4　正压负压加载示意图

此外，还应注意贴膜玻璃抗风压性能测试试件的制作。钢化玻璃为6 mm单片钢化玻璃，尺寸为1930 mm（宽）×864 mm（高）。首先将玻璃或贴膜玻璃放置于专用的铝合金型材框内，玻璃四边与型材框以至少5 mm厚的柔性垫块填充，两侧与铝合金框保证至少3.5 mm距离，先填塞柔性定位垫块或泡沫棒，再在外侧打注硅酮结构密封胶。安装于铝合金型材框架内的玻璃或贴膜玻璃试件四边通过夹具固定于风压测试设备洞口，试件安装如图5所示。

位移计是记录贴膜玻璃位移量的仪器设备。位移计的精度应达到满量程的0.25%，能较好地保证位移值的准确度，以使检测更为准确。位移计是测定构件的位移量的，其本身应该相对的稳定，因此位移计的安装支架在测试过程中应有足够的紧固性，并应保证位移的测量不受试件及其支承设施的变形、移动所影响。抗风压性能测试时，应至少布置3个位移计，位移计测点布置如图6所示，其中一个位移计位于面板中心，另两个位移计位于面板两侧，距离框100 mm内。

图5　试件安装图

挠度变形检测中，玻璃面板面法线挠度应按式（1）计算为

式中：fmax为面法线挠度值，mm；a0、b0、c0为各测点在预备加压后的稳定初始读数值，mm；a、b、c为某给定压力下各测点的面法线位移，mm。

即在某一压力下，面板最大位移出现在玻璃面板短边边长中点，以中间测点法线位移减去两端测点法线位移的平均值即为面法线挠度，其与有框幕墙玻璃短边边长的比值，即为测得的相对面法线挠度。面法线挠度的计算采用公式（1），是为了减去构件支承点的位移量，以使构件中部的位移值为真正的面法线挠度。

2　四边支承贴膜玻璃受弯承载性能分析

2.1有限元模拟计算结果分析

5 kPa均布荷载下6 mm未贴膜玻璃、贴膜玻璃（膜厚0.15 mm）的z轴最大变形量、第一主应力计算结果如图7所示。5 kPa时，6 mm未贴膜玻璃的挠度为19.95 mm，第一主应力为61.77 MPa；6 mm贴膜玻璃（膜厚0.15 mm）的挠度为19.855 mm，第一主应力为31.597 MPa。

图6　位移计测点布置图

图7　5 kPa均布荷载下6 mm玻璃贴膜前后挠度和第一主应力计算值图

由图7可知，5 kPa均布荷载下6 mm玻璃贴膜（膜厚0.15 mm）后挠度减少约0.1 mm，而第一主应力值减少约50%。

分别对未贴膜玻璃、贴膜玻璃（膜厚0.05、0.1和0.15 mm）在1、2、3、4和5 kPa均布荷载作用下的挠度和第一主应力进行模拟计算。不同压力均布荷载下贴膜前后玻璃挠度计算值如图8所示，均布荷载下贴膜前后玻璃第一主应力计算值如图9所示。

图8可以看出，未贴膜玻璃和贴膜玻璃在面均布荷载作用下，其z轴最大变形量与荷载呈线性变化趋势；与未贴膜玻璃相比，贴膜玻璃z轴最大变形量减小但不明显，说明贴膜玻璃的刚度有一定增加，但不明显；相同均布荷载下，不同贴膜厚度玻璃的挠度随着膜层厚度增加而减小但不明显，说明贴膜玻璃随着膜厚增加刚度有所增加，但不明显。

图8　贴膜前后玻璃挠度计算值图

图9可以看出，未贴膜玻璃和贴膜玻璃在面均布荷载作用下，其第一主应力与荷载呈线性变化趋势；与未贴膜玻璃相比，贴膜玻璃z轴第一主应力明显减小，约为未贴膜玻璃的一半，说明贴膜玻璃的强度增加了约1倍；相同均布荷载下，不同贴膜厚度玻璃的第一主应力随着膜层厚度增加而减小但不明显，说明贴膜玻璃随着膜厚增加强度有所改善，但不明显。

2.2挠度测试结果分析

膜层厚度为0.05、0.1、0.15 mm贴膜玻璃在不同均布荷载（正压）作用下挠度测试值如图10所示；膜层厚度为0.05、0.1、0.15 mm贴膜玻璃在不同均布荷载（负压）作用下挠度测试值如图11所示。

从图10、11可以看出，膜层厚度为0.05、0.1、0.15 mm贴膜玻璃挠度随着荷载值变化近似呈线性变化；贴膜玻璃膜层越厚，同一荷载作用下挠度普遍越大，但增加值很小。

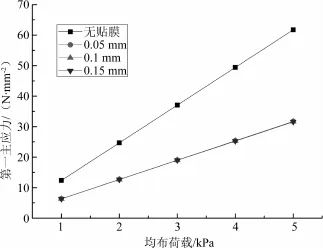
图9　贴膜前后玻璃第一主应力计算值图

图10　正压下贴膜玻璃挠度测试值图

图11　负压下贴膜玻璃挠度测试值图

同一压力（4 kPa）时正负压下挠度测试值见表2和图12。

图12可以看出，正负压挠度差值均在0.6～1.2 mm之间，说明贴膜面对玻璃挠度有一定影响，其中承受4 kPa相同压力时，贴膜面正压挠度变形与负压挠度变形大0.6～1.2 mm。

表2　6 mm厚玻璃同一压力（4 kPa）时正负压下挠度测试值

2.3模拟计算值与测试值对比分析

由于挠度计算采用的是弹性小变形模型进行的，而弹性小变形理论适用范围为：挠度不大于玻璃板厚度。因此，随着挠度与板厚之比加大，得到的挠度值有较大偏差，需按照相关标准规范予以修正［22］。JGJ 102—2003《玻璃幕墙工程技术规范》条文说明指出，四边支承玻璃面板采用了小挠度计算公式，考虑与大挠度分析方法计算结果的差异，将应力与挠度计算值予以折减，即按规范中公式6.1.3 -2及表6.1.2-2给出的折减系数对四边支承板进行折减。

图12　6 mm厚玻璃同一压力（4 kPa）时正负压下挠度测试值图

均布荷载下贴膜玻璃挠度计算值、修正值与测试值比较如图13所示。

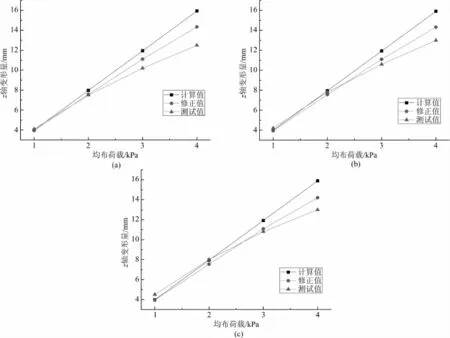
图13　均布荷载下贴膜玻璃挠度模拟计算与测试值比较图

图13可以看出，贴膜玻璃挠度计算值、测试值与均布荷载值呈近似线性趋势；随均布荷载值增大，贴膜玻璃挠度测试值呈先大于计算值，后小于计算值的趋势；在均布荷载大于一定值（约2 kPa）时，计算值大于测试值，说明计算值较为保守；修正后的计算值与测试值更为接近。

3　结论

通过对贴膜玻璃在不同风压下挠度和应力模拟和测试研究，得到如下结论：

（1）模拟计算结果表明，与未贴膜玻璃相比，均布荷载下玻璃贴膜后挠度减小但不明显，第一主应力值减小约50%，说明玻璃贴膜后刚度增加不明显，但强度增加了约1倍。膜厚的改变对贴膜玻璃的刚度和强度影响不明显。

（2）贴膜前后玻璃挠度试验研究表明，0.05、0.1、0.15 mm贴膜玻璃挠度随着荷载值变化近似呈线性变化。同一压力值下正负压挠度差值均在0.6～1.2 mm之间，说明贴膜面对玻璃挠度变形有一定影响，其中承受4 kPa相同压力时，贴膜面正压挠度变形与负压挠度变形大0.6～1.2 mm。

（3）挠度变形的模拟计算值和测试值比较结果表明，贴膜玻璃挠度计算值、测试值与均布荷载值呈近似线性趋势；随均布荷载值增大，贴膜玻璃挠度测试值呈先大于计算值，后小于计算值的趋势；在均布荷载大于一定值（约2 kPa）时，计算值大于测试值，说明计算值较为保守；修正后的计算值与测试值更为接近。

［1］ 龙文志.建筑玻璃贴膜［J］.新型建筑材料，2009，36（1）：72-74.

［2］ 贺勇，郭振黔，申屠文巍.中空贴膜玻璃在建筑节能外窗的应用［J］.墙材革新与建筑节能，2012（7）：56-58.

［3］ 曹毅然，张小松，杨伟华.双层中空玻璃镀（贴）膜遮阳效果的理论和实验研究［J］.建筑科学，2011，27（z1）：17-21.

［4］ 田学春，董孟能，谢厚礼.玻璃贴膜在建筑节能中的应用［J］.新型建筑材料，2009，36（8）：51-53.

［5］ 高嘉明，卢振，罗春燕.基于实测参数的玻璃贴膜节能效果评估方法［J］.建筑节能，2015（12）：91-93，114.

［6］ 吴永昌.建筑玻璃贴膜光学与热工性能研究［D］.广州：华南理工大学，2009.

［7］ 谢海容.贴膜窗户玻璃能耗的理论分析与实验研究［D］.长沙：湖南大学，2007.

［8］ 楚洪亮，孙诗兵，万成龙.贴膜隔热玻璃建筑节能效果模拟分析［J］.新型建筑材料，2015，42（12）：24-26，32.

［9］ 任鹏，王利民，何敏，等.贴膜玻璃抗冲击实验分析［J］.山东理工大学学报（自然科学版），2010，24（3）：10-13.

［10］万成龙，王洪涛，卢佳.贴膜玻璃残余抗风压性能试验研究［J］.建设科技，2014（12）：47-49，54.

［11］GJ/T 351—2015.建筑玻璃膜应用技术规程［S］.北京：中国建筑工业出版社，2015.

［12］原方，邵兴，陈丽，等.工程力学［M］.北京：清华大学出版社，2006.

［13］徐鹤山.ANSYS建筑钢结构工程实例分析［M］.北京：机械工业出版社，2011.

［14］李章政.弹性力学［M］.北京：中国电力出版社，2011.

［15］陶志雄，张其林，陈俊，等.四边简支夹层玻璃受弯承载力试验研究及有限元分析［J］.建筑结构学报，2010，31（10）：114-119.

［16］陶志雄，张其林，陈俊，等.基于ANSYS二次开发的夹层玻璃面板有限元分析［J］.计算机应用与软件，2011，28（5）：8-11.

［17］王勋，张其林，陶志雄，等.四边简支夹层玻璃承载性能理论和试验研究［J］.建筑结构，2012，42（2）：173-175.

［18］陈俊，张其林，谢步瀛.基于APDL的夹层玻璃面板非线性有限元分析［J］.计算机辅助工程，2010，19（1）：22-26.

［19］张治权.夹层玻璃落球冲击剥离性能研究［D］.杭州：浙江大学，2013.

［20］康小洪，聚对苯二甲酸乙二醇酯［EB/OL］.http：//baike. baidu.com/view/950058.htm#ref_［1］_950058，2012-08-13.

［21］塑料原料参数库.中塑在线［EB/OL］.http：//www.21cp.com/ techpara/14104.htm，2016-04-04.

［22］GJ 102—2003.玻璃幕墙工程技术规范［S］.北京：中国建筑工业出版社，2003.

［23］张其林.玻璃幕墙结构设计［M］.上海：同济大学出版社，2007

Analysis of flexural bearing performance of filmed glass supported
on four sides

Wan Chenglong1，3，Lu Jia2，Sun Shibing1*，et al.

（1.College of Materials Science and Engineering，Beijing University of Technology，Beijing 100124，China；2.3M China Ltd.，Co.，Beijing 100004，China；3.China Academy of Building Research，Beijing 100013，China）

The film is one of the methods to prevent non-safety glass or toughened glass instantaneous shedding after being broken off，which can provide enough time for security isolation measures and maintenance.Flexural performance research of filmed glass has an important guiding significance for the engineering application.Deformation along z axis direction and the first principal stress value of glass and filmed glass under 1，2，3，4 and 5 kPa uniformly distributed load are studied based on finite element simulation method.The results show that z axial deformation is not obvious for glass and filmed glass with different thickness film layer and first principal stress is reduced by about 50%after being filmed.z axis deformation with load change is approximately a linear change under 1，2，3 and 4 kPa，and deflection deformation of filmed glass under positive pressure is slightly larger than that of negative pressure.Comparisons of simulation and test show that z axis deformation is approximately a linear trend with uniformly distributed load value，and test values of z axis deformation are higher than those of the calculated and then less than the calculated with uniformly distributed load increasing，indicating that the simulation results are more conservative and the modified simulation values areclose to the tested ones.

four-side support；filmed glass；flexural bearing performance

TU524

A

1673-7644（2016）04-0350-08

2016-05-07

北京市科技计划课题项目（Z141100006014054）

万成龙（1983-），男，工程师，硕士，主要从事透明围护结构等方面的研究.wan_chenglong@163.com

*：孙诗兵（1963-），男，高级工程师，博士，主要从事建筑围护结构节能材料与技术等方面的研究.E-mail：sunshibing@bjut.edu.cn