巧破抛物线小题的几个实用结论

安徽省和县三中 范世祥

巧破抛物线小题的几个实用结论

安徽省和县三中 范世祥

纵观近几年全国各省市的高考题，抛物线时常作为一道小题来考查。一些考生因为一时未能找准思路，从而陷入大量烦琐的运算之中，即使解答出来了，也花了很大的“成本”，从而导致时间不够用，无法顺利完成后面的试题。为此，笔者总结了一些可以快速攻破抛物线小题的切实可行的结论，掌握、运用好这些结论可以取得“精、准、快”的解题效果。

一、弦端点坐标问题

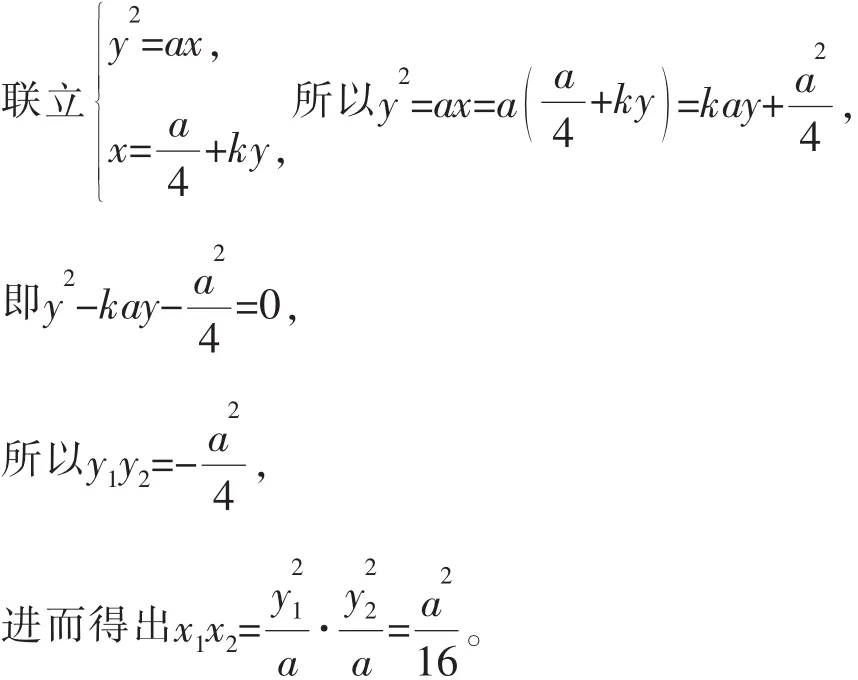
结论2 （结论1的推广）已知直线l与抛物线y2=ax（a＞0）相交于点A（x1，y1）、B（x2，y2），且与x轴相交于点M（m，0），则有x1x2=m2，y1y2=-am。（证明略）

例1 已知F是抛物线y2=x的焦点，点A、B在该抛物线上且位于x轴的两侧，O→A·O→B=2（其中O为坐标原点），则△ABO与△AFO面积之和的最小值是_______。

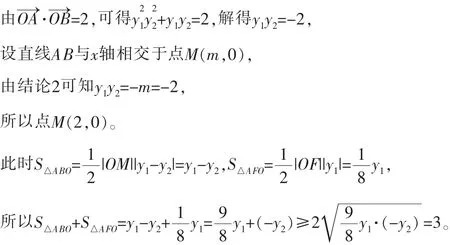
二、焦点弦长问题

结论3 已知AB是抛物线y2=ax（a＞0）的焦点弦，且A（x1，y1），B（x2，y2），点F是抛物线的焦点，则有。

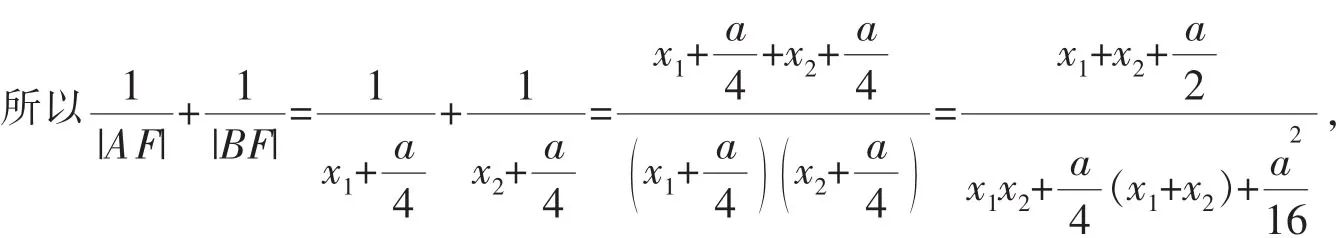
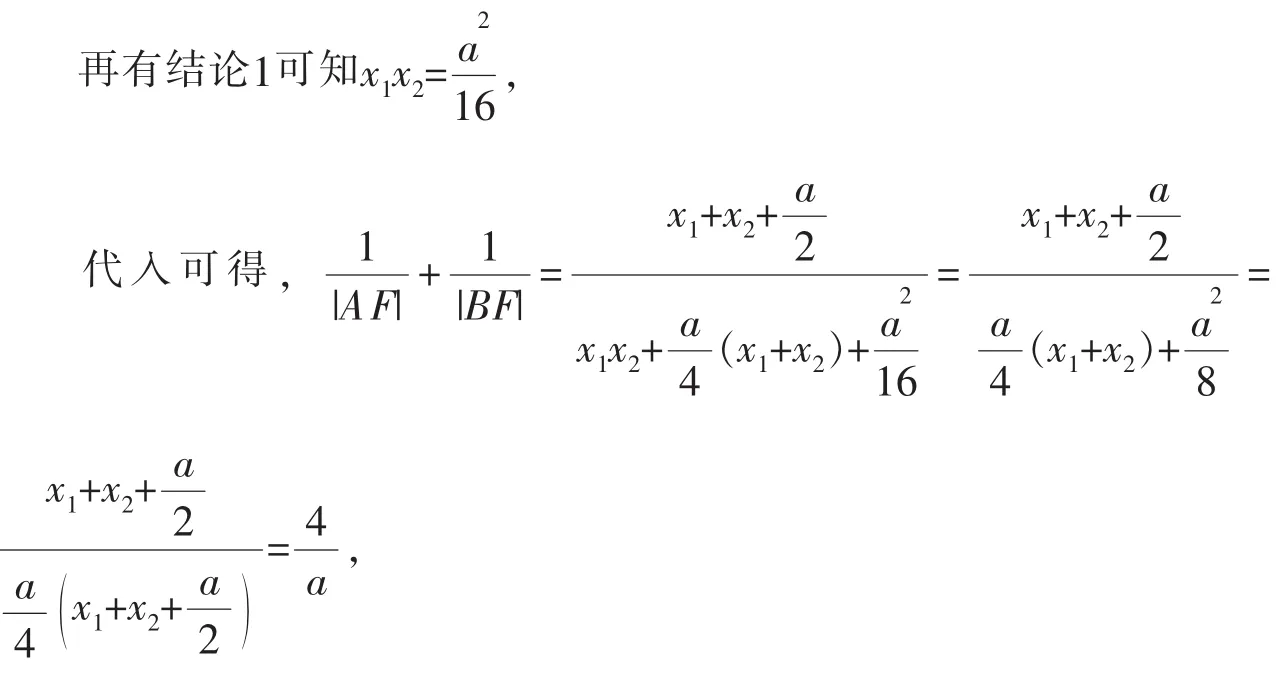
结论4 已知AB是抛物线y2=ax（a＞0）的焦点弦，且A（x1，y1），B（x2，y2），点F是抛物线的焦点，则有（θ为直线AB的倾斜角）。

例2 过抛物线y2=4x的焦点F的直线交该抛物线于A、B两点，若|AF|=3，则|BF|=_______。

三、焦点三角形面积问题

例3 设F为抛物线C：y2=3x的焦点，过F且倾斜角为30°的直线交C于A、B两点，O为坐标原点，则△OAB的面积为_______。

四、以极点和极线为背景的问题

结论6 设AB为抛物线的焦点弦，则该抛物以A、B为切点的切线的交点轨迹是它的准线；反之，由抛物线准线上任一点向抛物线引两条切线，切点为A、B，则AB为焦点弦。

证明 设抛物线y2=2px（p＞0），

则点A、B处的切线方程分别为y1y=p（x+x1）和y2y=p（x+x2），

设两切线的交点为M（x0，y0），则有y1y0=p（x0+x1），y2y0=p（x0+x2）。

这说明切点A（x1，y1），B（x2，y2）都在直线y0y=p（x+x0）上，

因此直线AB的方程为y0y=p（x+x0），

将焦点坐标代入直线AB的方程y0y=p（x+x0）后得到，

即两切线交点M（x0，y0）在准线l：上。

反之，设抛物线y2=2px（p＞0），点A（x1，y1），B（x2，y2），

因为抛物线在点A、B处的切线方程可分别表示为y1y=p（x+x1）和y2y=p（x+x2），且切线均经过，

这说明切点A（x1，y1），B（x2，y2）都在直线上，

结论7 若抛物线的两条切线相互垂直，则这两条切线的交点的轨迹是它的准线；反之，由抛物线准线上任一点向抛物线引两条切线，这两条切线必互相垂直。

证明 设自一点M（x0，y0）向抛物线y2=2px（p＞0）所引切线的方程为y=k（x-x0）+y0（k≠0），

即由抛物线的准线上任一点引抛物线的两切线必互相垂直。

解析几何中像这样可以引申、推广的规律有很多。只要我们平时经常总结、归纳同类题的解题方法，并注意探究和发掘变换事物中所蕴含的一般规律，就一定会有更多惊喜的发现。