一类非线性Schrödinger-Kirchhoff系统基态解的存在性
吴晓蕾
(吕梁学院数学系,山西离石033000)
一类非线性Schrödinger-Kirchhoff系统基态解的存在性
吴晓蕾
(吕梁学院数学系,山西离石033000)
文章主要利用变分方法讨论带有周期位势V(x),但不含(AR)条件的Schrödinger-Kirchhoff型方程基态解的存在性。
Schrödinger-Kirchhoff型方程;基态解;变分法;临界点
文章主要讨论下面的Schrödinger-Kirchhoff型方程
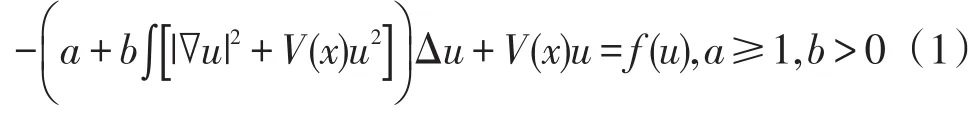
在(1)中,若V(x)=0,则对应的方程为kirchhoff型方程;若b=0,则对应的方程为Schrödingerpoisson方程。这种类型的方程起源于数学物理现象,且应用十分广泛。例如在研究定波逆射的时候,就涉及到此问题,其中方程的解为相应的扩散反应方程的稳定点,而这种反应扩散方程在化学动态系统现象中也形成了模型。近年来,国内外学者主要研究了这两类方程的超线性及渐进线性问题,周期及非周期性问题,径向对称问题等[1-3]。事实上,研究这类问题难点有两个:一是(ps)序列或(Ce)序列的有界性;二是嵌入的紧性。本篇文章在上述知识的基础上,利用变分方法克服了这两个问题,讨论了(1)的基态解的存在性。
为讨论方便,f∈C(R3,R),f(0)=0,
还需要满足下列假设条件:

对x∈R3,y∈Z3一致成立;

(H3)存在c>0,p∈(2,4)使得对任意s∈R+,|f(s)|≤c(s+|s|p-1);
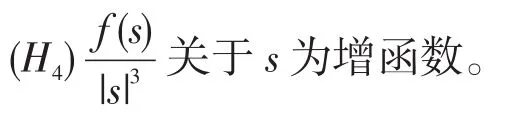
引理1若 {un}⊂M为I的一个(Ce)序列,即(1+||un||)I'(un)→0),而且有I(un)有界,则{}un有下列特点:
1)存在h>0,limn→i∞n f ||un||≥h;
2){un}⊂M有界;
证明1)由(H2),(H3)得F(s)≤εs2+Cεsp,则

由于p∈(2,4),ε→0,于是泛函I有下界。即
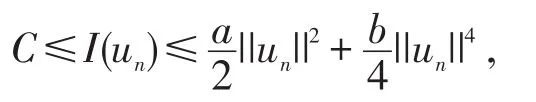
因此存在h>0,满足
2)假设{un}无界,令则||wn||=1,存在子列使得在M上,在(2≤p<6)上,wn→w;几乎处处在R3上wn→w。此时有下列两种可能情形。
情形1:若w≠0,我们有一方面
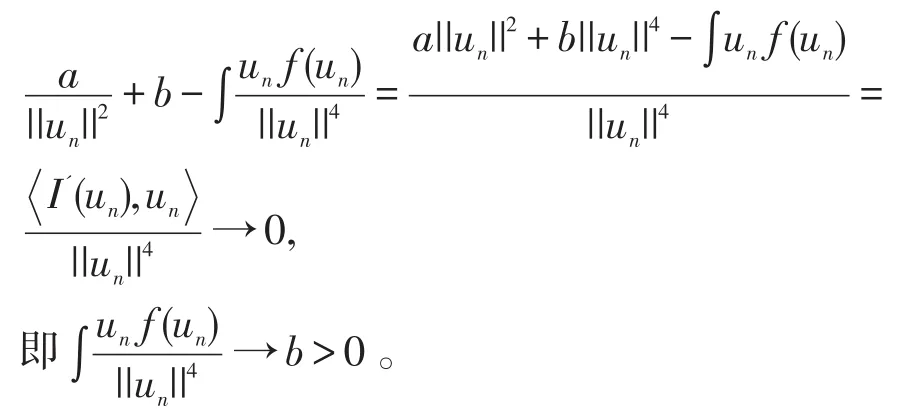
另一方面,在Ω={x∈R3|w(x)≠0}上

由于|Ω|>0,利用Fatou引理得
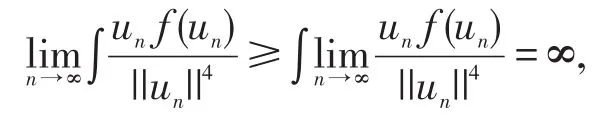
矛盾。
情形2:若w=0,取yn∈Z3,定义
vn=wn(x+yn),由于V(x)为周期函数,我们有||vn||=||wn||=1,|vn|p=|wn|p,I(vn)=I(wn),则存在弱收敛的子列{vn} ,在M上,;在上(2≤p<6),vn→v;几乎处处在R3上vn→v。若存在yn,满足
将会得到与w≠0同样的矛盾。假设存在yn,使,所以对任意p∈(2,4)有
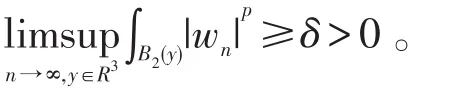
否则,将存在p∈(2,4),δ>0,zn∈R3满足
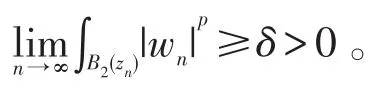
取yn∈B2(zn),B1(yn)⊂B2(yn),从而,即


而a≥1矛盾,因此{un}有界。
结合1)我们可得到下面矛盾

引理2V满足(V0),f满足(H2),(H3),则存在r>0,e∈M,||e||>r使得
证明由于I(u)有下界,则显然存在b,r有||u||=r}>I(0)=0。因为由(H2),(H3)得到存在C>0,任意M>0有F(s)≥Ms4-Cs2,于是
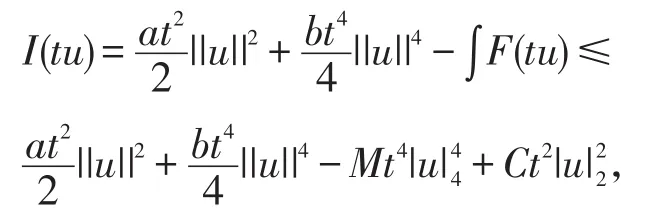
当M>0充分大,t→∞时,记e=tu,显然满足||e||>r且I(e)<0=I(0)。
由山路定理[4]知,存在(Ce)序列{}un满足
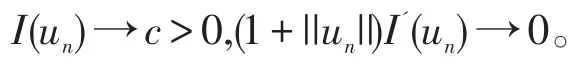
定理1V,f分别满足假设条件(V0),(H2)-(H4),则系统(1)至少存在一个基态能量解。
证明引理1,引理2说明了u为系统(1)的非平凡解,且I(u)≥c,接下来证I(u)=c。结合Fatou引理可得
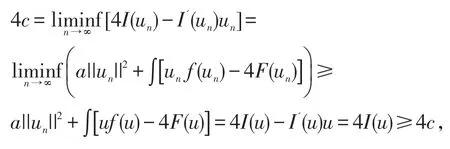
因此I(u)=c,u为系统(1)一个基态解。
[1]APRILE T D,MUGNAI D.Solitary waves for nonlinear Klein-Gordon-Maxwell and Schrödinger-Maxwell equations[J].Proc Roy Soc Edinburgh Sect A,2004(134):893-906.
[2]COCLITE G M,GEORGIEV V.Solitary waves for Maxwell-Schrodinger equations[J].Differential Equations,2004(94):1-31.
[3]WU X.Existence of nontrivial solutions and high energy solutions for Schrödiger-Kirchhoff ty-pe equations inRN[J].Nonlinear Anal.2011(12);1278-1287.
[4]王术.Sobolev空间与偏微分方程理论[M].北京:科学出版社,2009.
〔责任编辑 高海〕
Existence of the Ground State Solution for a Class of the Nonlinear Schrödinger-Kirchhoff System
WU Xiao-lei
(Department of Mathematics,Luliang University,Lishi Shanxi,033000)
In this paper,we study existence of the ground state solution for a class of the non-linear Schröddinger-Kirchhoff system with period potentialV(x)and without(AR)condition by variational method.
Schrödinger-kirchhoff system;the ground state solution;variational method;the critical point
O177.91
A
1674-0874(2016)03-0024-03
2016-03-08
吴晓蕾(1987-),女,山西运城人,硕士,助教,研究方向:非线性泛函分析与非线性微分方程。

