基于Lévy飞行的人工蜂群算法

程宪宝

（广州工商学院，广东广州510850）

基于Lévy飞行的人工蜂群算法

程宪宝

（广州工商学院，广东广州510850）

针对人工蜂群算法在后期容易陷入局部最优，且开发能力不足的缺陷，提出了一种基于Lévy飞行的人工蜂群算法，在寻找蜜源过程中，引领蜂转变成侦查蜂时，引入Lévy分布函数来调配原有的用0-1的随机数参与的贪婪算法，有效增加了算法的合理性。最后用5个有效的测试函数对改进的算法和原算法进行比较，结果表明，基于Lévy分布的人工蜂群算法较原算法在收敛速度和优化速度上都有显著提高。

ABC;优化；Lévy分布；仿真

人工蜂群算法[1](Artificial Bee Colony Algorithm,ABC)是一种以蜂群内部自组织和群体智能为基础的仿生学优化算法。ABC算法原理简单，参数少，易于实现，有较强的全局寻优能力，已经快速成为优化领域中强有力的全局优化工具之一[2-6]。同时，和众多的仿生学优化算法类似，ABC算法由于进化方式和选择策略的影响，该算法在接近全局最优解时，也存在搜索速度变慢、种群多样性减少、容易陷入局部最优等缺点,因此本文提出了一种基于Lévy（莱维）分布[7]的改进人工蜂群算法，可以有效提高算法后期全局最优的开发，并且局部搜索能力上比原算法有显著提高。

1 人工蜂群算法

1.1 ABC算法概述

ABC算法是模拟自然界中蜜蜂群体采蜜行为的一种智能算法。蜜蜂个体只能进行简单的动作，但是其群体却表现出非常智能的行为，在寻找蜜源、采集蜂蜜、传递信息等方面精准到位。在ABC算法中，将群体蜜蜂分为三种，引领蜂、跟随蜂、和侦查蜂。引领蜂负责采集蜂蜜和招募蜜蜂，跟随蜂根据引领蜂所传递的信息按一定的规则选择引领蜂进行跟随，侦查蜂负责开发新的蜜源。在寻优问题中，每个蜜源表示问题的一个可能解，蜜源质量的好坏用解的适应度值来表示。适应度值高的解所代表的食物源会优先被引领蜂采集，跟随蜂会在食物源的周围进行侦查，以期发现更优的蜜源，每发现一个蜜源，就会与原蜜源进行比较，如果新的蜜源的质量比原蜜源更好，则淘汰原蜜源，并随即在新的蜜源周围继续重复原来的搜索。经过这样多次搜索就可以确定适应度值最高的解，即问题的最优解。如果蜜蜂个体在一个蜜源附近经过Limit次的搜索都没有更新蜜源时，则放弃该食物源，并记录其适应度值，随即变成侦查蜂去寻找新的食物源。

1.2 ABC算法步骤

(1)问题的初始化

蜜蜂寻找食物源的过程就是寻优问题找最优解的过程。首先算法随机生成一个初始种群，这个初始种群中包含N个可行解，解的数量和引领蜂的数目相等。每个解xi(i=1,2,…N)用一个D维向量xi(xi1,xi2,…xiN)来表示。D指待解决问题的参数的个数，即问题的维数。初始解的生成引入一个随机参数，按照式1生成。

式中d∈(1,2,…N)，xid.min和xid.max分别是xid的上限和下限：rand为随机生成的在（0，1）之间均匀分布的随机数。

利用下式计算各蜜源的质量（适应度值）：

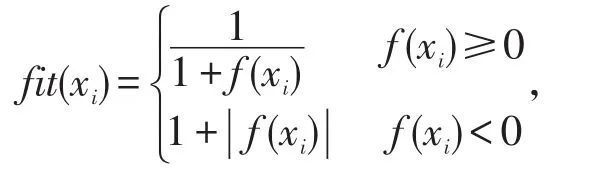
式中fit(xi)表示第i个食物源xi的蜜源质量，即第i个解的适应度值，f(xi)表示该点对应的目标函数值。

(2)引领蜂搜索

引领蜂会在每个食物源周围进行搜索，按照“贪婪算法”的思想进行优胜劣汰，在搜索次数未达到预定的次数之前，一直循环进行。ABC算法对食物源xi的邻域进行搜索，依据式（2）产生新的食物源vi(vi1,vi2,…viN)。

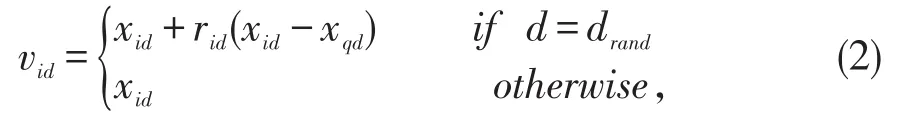
式中，q为[1,N]间的随机整数，且q≠i，即根据上式生成新的蜜源xq=(xq1,xq2,…xqD)，且xq与xi不同，drand为[1,N]之间的随机整数，rid∈[-1,1]是一个-1到1之间的随机整数，用来控制引领蜂邻域搜索范围。

由式(2)可以看出，随着xid和xqd的差值逐渐减小，新位置的产生的波动也越来越小，随着循环的进行，搜索会渐渐接近最优解，xid-xqd会自适应的减少，因此算法具有自适应的收敛性。

(3)跟随蜂的搜索

当引领蜂完成搜索后，会记下蜜源相关信息(质量、方向、距离等)飞回蜂巢，在特定区域以“8”字舞或“摇摆”舞或其它方式向跟随蜂传递蜜源信息。跟随蜂以轮盘赌的方式选择蜜源，质量好且距离近的蜜源会招募到较多的跟随蜂，蜜源i被跟随蜂选中的概率p(xi)依据式（3）产生。

跟随蜂根据引领蜂所传达的信息到达所选择的蜜源位置后，在蜜源周围利用式(2)进行邻域搜索，和引领蜂一样利用“贪婪算法”优胜劣汰进行选择。

(4)引领蜂和侦查蜂的转换

引领蜂根据“贪婪算法”选择后，如果经过Limit次后都没有更新蜜源，表明在当前邻域中所选择的蜜源已经是质量最好的，即当前解是局部最优解，从算法的角度讲，算法已陷入局部最优，该蜜源应该被放弃。此时，引领蜂转换成侦查蜂，算法根据式(1)重新生成新的蜜源。找到蜜源后侦查蜂又重新变成引领蜂，重复算法搜索过程。

(5)结束

如果搜索达到预先设定好的循环最大次数，或是根据所求问题精度需要，达到程序结束条件，则算法结束，完成搜索。

2 算法的改进

ABC算法存在问题的根本原因在于在后期无法保持群体的多样性，侦查蜂在寻找新的密源时，是采用0～1之间的一个随机数来调配“贪婪算法”，群体活动趋于统一，并且在寻找到局部最优解后无法快速向全局最优解前进，开采能力不足，算法很容易陷入局部最优。为此很多研究者采取了多种优化方法，并取得了一定的成绩。文献[8]加入局部搜索算子，对当前的最优蜜源进行局部搜索，以改进算法易早熟的缺点。文献[9]提出一种动态调整子种群个体数目，以增强其局部搜索能力。文献[10]在算法中引入一维正态云模型和新的概率选择策略来提高算法的后期搜索能力。

本文在前人研究的基础上，将符合自然界中飞行物种实际觅食习惯的Lévy飞行引入到算法中。研究表明很多动物和昆虫的觅食行为具有莱维飞行的典型特征[11]，目前，这种行为己经被运用到优化和优化探索方面[12]。在引领蜂经过Limit次搜索没有发现比当前蜜源质量更好的蜜源时，便和侦查蜂转换，此时采用Lévy（莱维）分布来代替随机分布如式（4）所示。Lévy分布其实是随机点分布的一种形式，在这种分布中，短距离的点分布与长距离的运动线之间相互参杂，研究表明Lévy对群体协作又相互独立的觅食者来说，是最理想的寻找策略。Reynolds等人对蜜蜂和果蝇觅食轨迹进行观察，发现其飞行轨迹中也呈现出Lévy Flight特征[13-14]

改进后算法的流程图如图1所示：

图1 改进算法的流程图

3 实验仿真

3.1 测试函数

为了验证改进的人工蜂群算法在实际的寻优过程中的有效性，选取5个常用的测试函数进行测试，并将改进的蜂群算法(LABC)和原算法(ABC)进行比较，这5个测试函数有两个单蜂函数和3个多峰函数组成，可以有效测试算法的寻优能力和抗干扰能力,见表1，仿真数据以最优值，最劣值，平均值和收敛性表示，收敛性=(最劣值-最优值)/平均值，可以反应算法的收敛速度。

表1 测试函数

3.2 仿真结果与分析

表2为仿真的结果。图2～6为改进算法对5个测试函数的求解变化趋势，其中，函数F1、F3为迭代次数为2000，D=60时的仿真效果，F2、F4、F5设置迭代次数为2000，D=30，每个函数的效果图都是50次优化平均得到的结果。

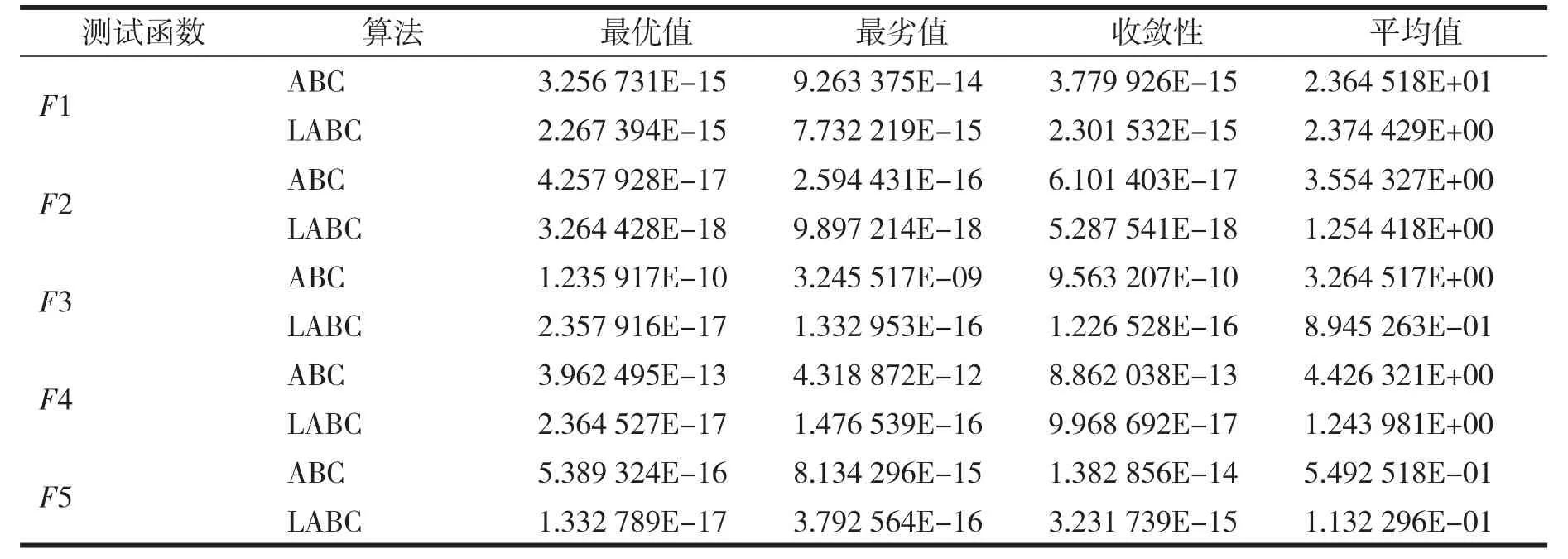
表2 两种算法的性能比较

图2 F1函数

图3 F2函数

图4 F3函数

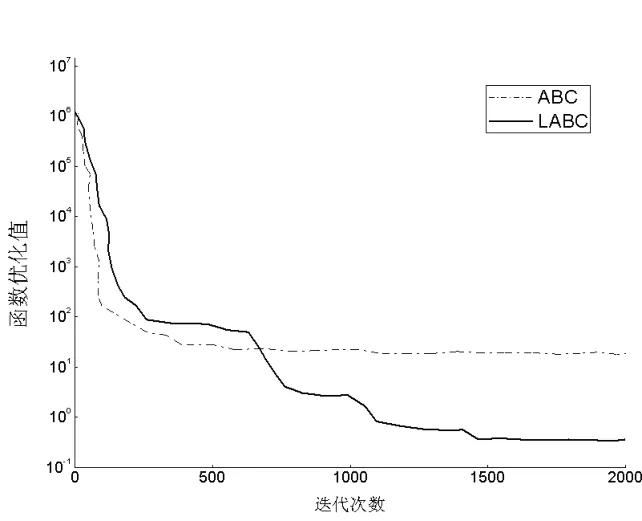
图5 F4函数

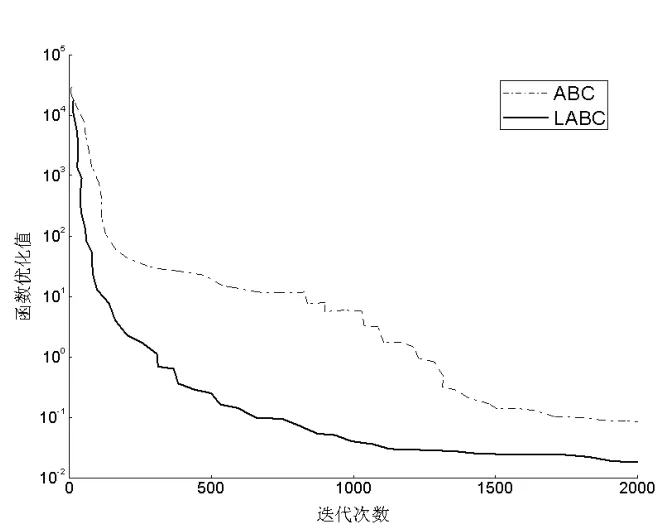
图6 F5函数

从仿真的结果可以看出，基于Lévy分布的人工蜂群算法与ABC相比，在收敛速度和寻优速度上都有所提高。

4 结束语

在当今科学研究领域，多学科相互交叉，相互渗透是现代科学技术发展的显著特点之一，各种仿生智能算法也越来越多的和其它理论结合起来以提高其优化效果。人工蜂群算法由于算法简洁，参数较少而在近年来受到广泛关注，但它和重多的仿生智能算法一样，容易坠入局部最优而放弃全局最优值，后期开采能力弱。本文将更符合昆虫觅食实际运动行为轨迹的Lévy分布加入到人工蜂群算法中，有效提高了算法的收敛速度、优化速度和算法的运行效率。

[1]KARABOGA D.An Idea Based On Honey Bee Swarm for Numerical Optimization[R].Turkey：Erciyes University,2005.

[2]PARK,J Y,HAN S Y.Swarm Intelligence Topology Optimization Based on Artificial Bee Colony Algorithm[J].International Journal of Precision Engineeringand Manufacturing,2013,14(1)：115-121.

[3]XU Y F,FAN P.A Simple and Efficient Artificial Bee Colony Algorithm[J].Mathematical Problems in Engineering,2013.

[4]BANSAL,J C,SHARMA H.Memetic search in artificial bee colony algorithm[J].Soft Computing,2013,17(10)：1911-1928.

[5]KASHAN M H,NAHAVANDI N.DisABC：A new artificial bee colony algorithm for binary optimization[J].Applied Soft Computing,2012,12(1)：342-352.

[6]KARABOGA N,CETINKAYA M B.A novel and efficient algorithm for adaptive filtering：Artificial bee colony algorithm[J].Turkish Journal of Electrical Engineering and Computer Sciences,2011,19(1)：175-190.

[7]SPRINGER X S,YANG.Firefly Algorithm,Levy Flights and Global Optimization[M].Research and Development in Intelligent Systems XXVI：Berlin,209-218.

[8]刘三阳,张平,朱明敏.基于局部搜索的人工蜂群算法[J].控制与决策，2014，15(1)：123-128.

[9]龙文,赵东泉,徐松金,等.子种群个体动态调整的人工蜂群算法[J].兰州理工大学学报，2015，41(6)：93-98.

[10]李仁兴,丁力.基于云模型蜂群算法的无人机航迹规划[J].计算机科学，2015，42(11A)：89-92.

[11]PAVLYUKEVICH.Levy flights,non-local search and simulated annealing[J].Journal of Computational Physics，2007，226：1830-1844.

[12]SHLESINGER M.Search research[J].Nature，2006，443：281-282．

[13]LIU C,YE C M.Bat algorithm with the characteristics of Levy flights[J].CAAI Transactions on Intelli gent Systems,2013,8(1)：240-246.

[14]XIE J,ZHOU Y Q,CHEN H.A bat algorithm based on Levy flights trajectory[J].Pattern Recognition and Artificial Intelligence,2013,26(9)：829-837.

〔责任编辑 高海〕

An Artificial Bee Colony Algorithm Based on Lévy Flight

CHENG Xian-bao
(Guangzhou Collage of Technology and Business,Guangzhou Guangdong,510850)

The artificial bee colony algorithm in the later is easy to fall into local optimum,and the lack of ability to develop This paper proposed a kind of artificial bee colony algorithm based on Lévy flight,in the process of finding nectar,leading bees turn into scout bees,the introduction of Lévy distribution function to allocate raw some 0-1 random number in the greedy algorithm,which effectively increased the rationality of the algorithm.Finally,the improved algorithm and the original algorithm are compared with 5 effective test functions,and the results show that the algorithm based on Lévy distribution has significantly improved the convergence speed and the optimization speed.

ABC;optimization;Lévy distribution;simulation

TP301.6

A

1674-0874(2016)03-0012-05

2016-03-09

程宪宝(1978-)，男，山东菏泽人，硕士，讲师，研究方向：智能计算及计算机应用。