一类时滞边界反馈控制系统的精确能控性研究

张 卓，杨 晨

（山西大学商务学院基础教学部，山西太原030031）

一类时滞边界反馈控制系统的精确能控性研究

张 卓，杨 晨

（山西大学商务学院基础教学部，山西太原030031）

研究一类具有时滞边界反馈控制的Euler-Bernoulli梁震动系统在初值条件下的精确能控性.作者首先选择了适当的状态线性空间M,引入了输入、输出算子B、C,并证明了系统可写成M上的状态反馈控制系统∑(A,B,C)。最终通过研究算子性质证明其在线性空间M上不具备精确能控性。

时滞；边界反馈控制；精确能控性

本文研究一类具有时滞边界反馈控制的梁震动系统

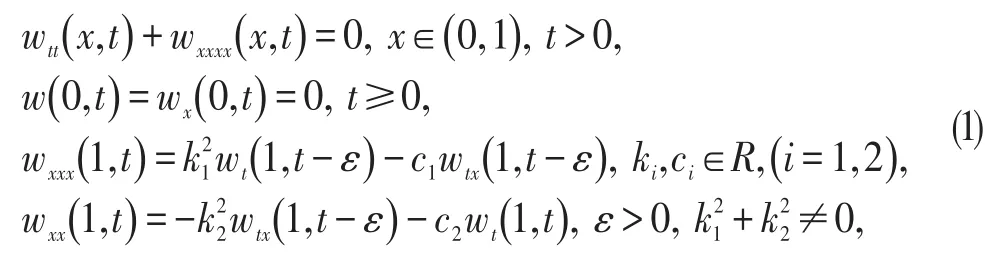
在初值条件

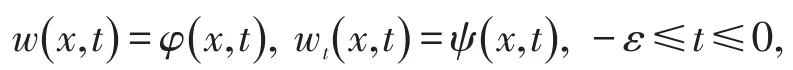
下的精确能控性。在该系统中,各变量的物理意义如下：w(x,t)为横向位移,wt(x,t)为速度,wx(x,t)=θ为旋转角,wtx(x,t)为角速度,-wxx(x,t)=M为弯矩,wxxx(x,t)=V为剪力。

Euler-Bernoulli梁震动系统的适定性、稳定性、精确能控性在工程，物理，化学，电子，机械，生物等诸多领域都有重要的研究价值，见文献[1-2]。在这些文章中，作者用基扰动法，牛顿迭代法，半群法等研究了具有边界控制的Euler-Bernoulli梁方程的适定性，稳定性，精确能控性等。但在实践中总是难以避免存在时滞，于是这方面的研究也很活跃，如文献[3]中关于时滞系统的稳定性、非线性、辨识、时滞消除与利用技术等方面的研究，取得了许多成果，包括时滞辨识、两种基于时滞方程的控制律的设计方法、时滞正反馈控制技术、时滞实验等。

不同于上述文章，为研究的需要，本文首先选取了适当的状态线性空间M,引入辅助系统，将其改写为M上的状态方程∑(A,B,C)。其中A是M上的强连续半群的生成元,B,C均为无界算子。作者最终是通过研究算子的性质证明该震动系统在线性空间M上是不具备精确能控性的。

1 预备知识

状态线性系统∑(A,B,-)精确能控性的相关知识：

（1）∑(A,B,-)在[0,τ]上的能控映射Bτ满足：

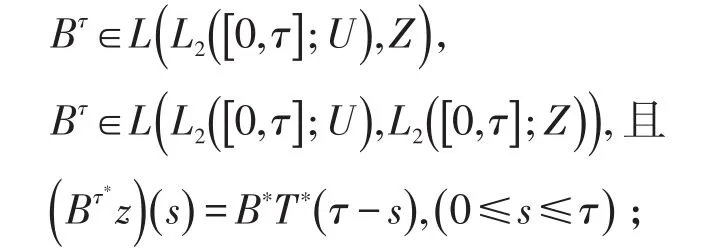
（2）∑(A,B,-)在[0,τ]上的能控域满足：

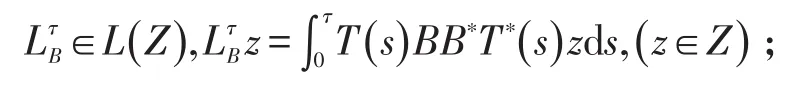
（3）∑(A,B,-)在[0,τ]上精确能控当且仅当对于某个γ＞0和∀z∈Z，下列条件之一成立：

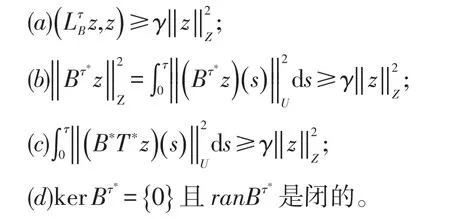
2 状态线性系统的建立

首先研究相应的无时滞系统：

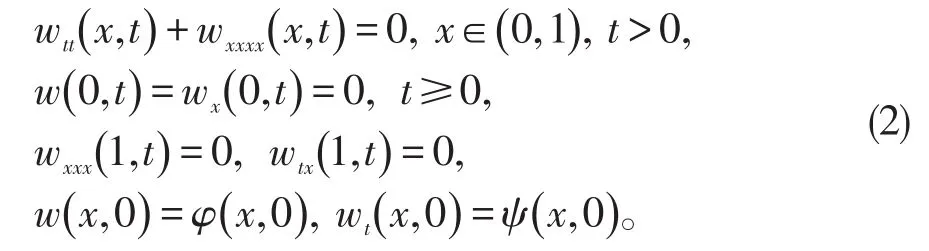
定义算子

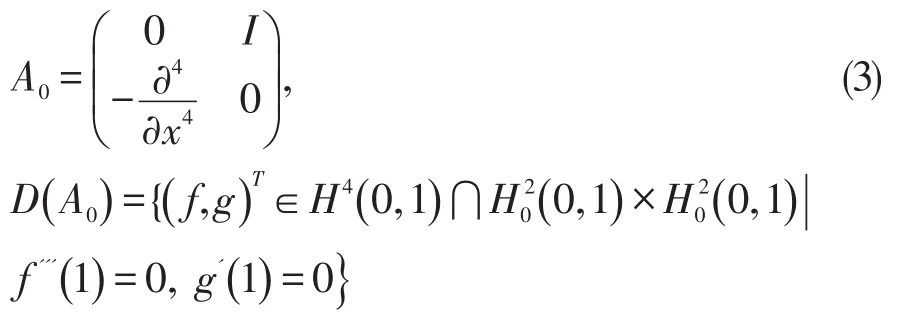
令x(t)=(w(·,t),wt(·,t))T, 其中w(·,t)是方程 (2)的解，则系统(2)可写成Cauchy方程：

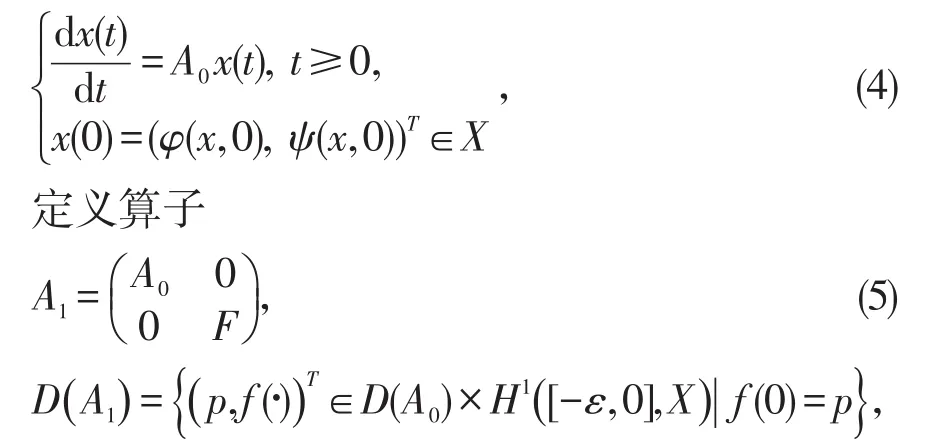
其中A0如(3)定义，M,及内积 ((p,f(·))T,(q,g(·))T)M见文献[1]。

这里H1([-ε,0],X)={f：[-ε,0]→X|f在 [-ε,0]上绝对连续，且f'(·)∈L2([-ε,0],X)} 。又D(A1)到M是紧嵌入,故A1有紧的预解算子。

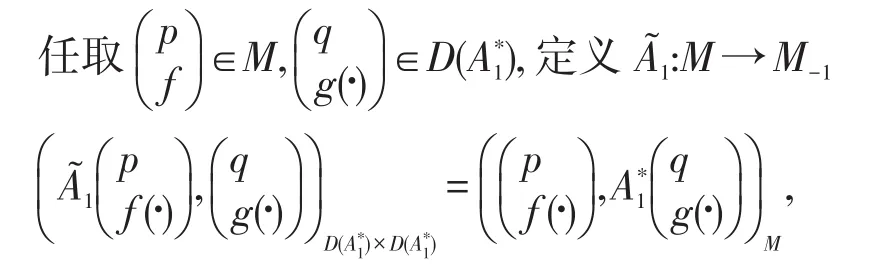
为A1的延拓算子，则为方便，仍用A1表示1。用同样的方法延拓A0，使A0∈L(X,X-1)。

令

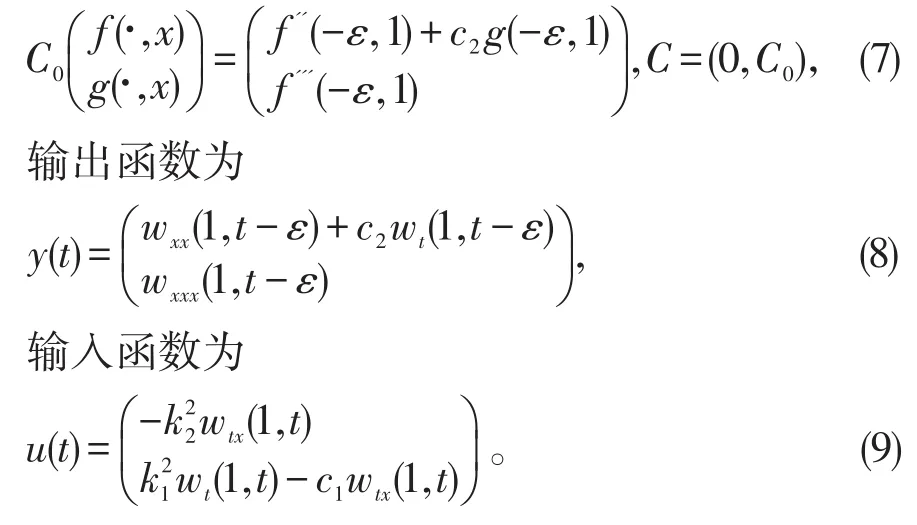
定理1 设A1如（5）定义C,u(t),y(t),如（6）～（9）定义，则系统（1）可写为M上的状态反馈控制系统：

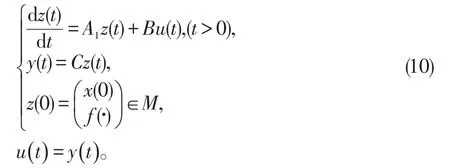
3 精确能控性

定理2 若B如（6）定义，则

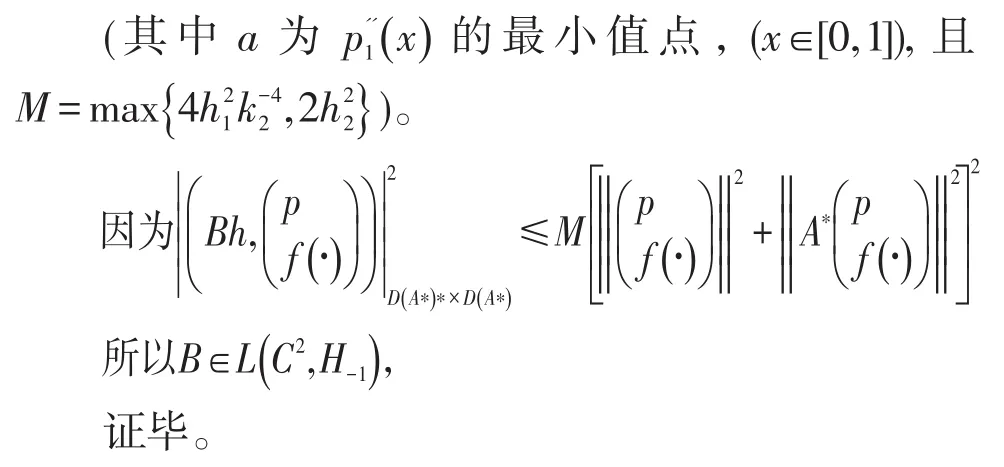
定理3设T(t)为A1生成的C0-半群，则∀ε＞0，系统(I)在[0,ε]上不精确能控。

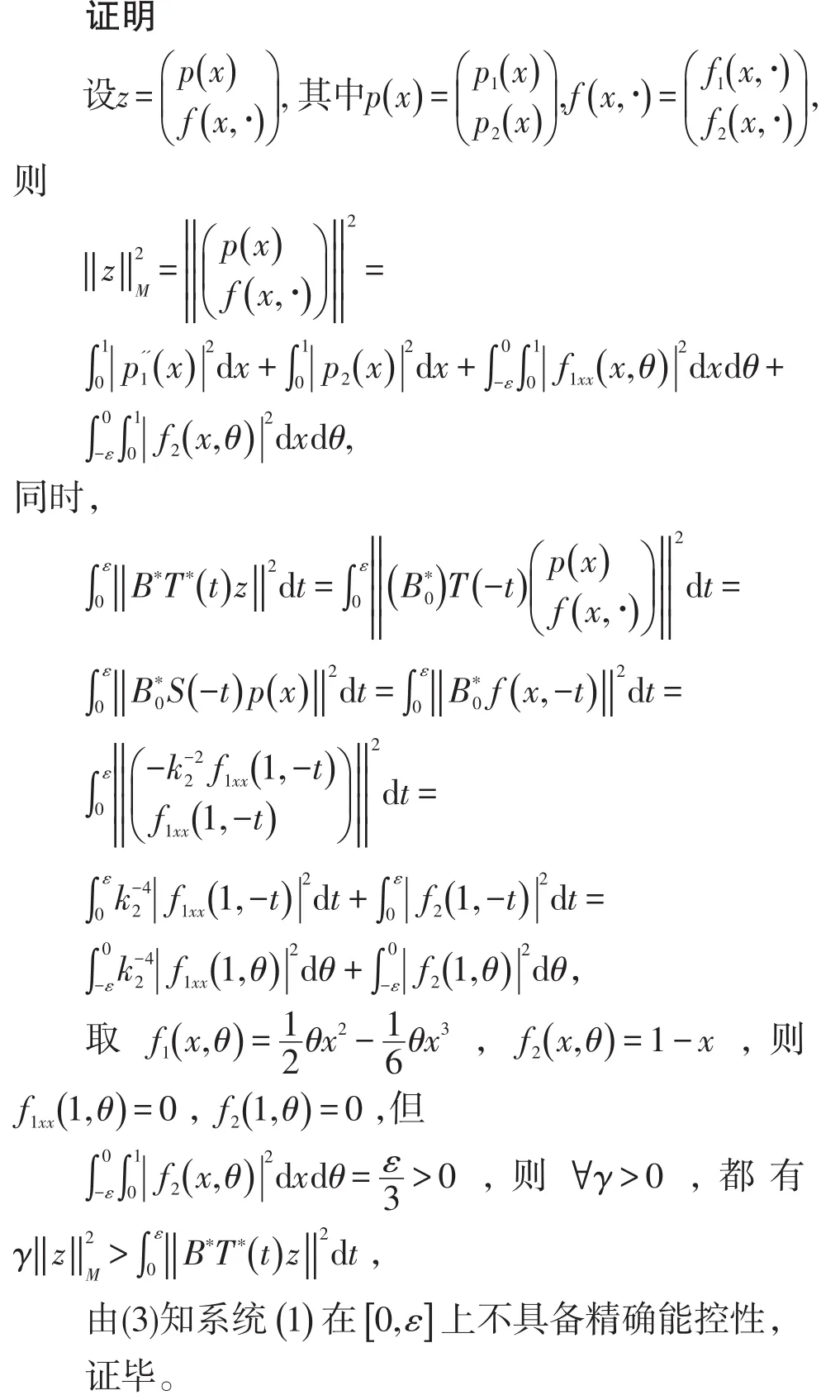
综上，通过选择适当的状态线性空间，改写系统，研究算子性质，文中证明了该类具有时滞边界反馈控制的Euler-Bernoulli梁震动系统在初值条件下是不具备精确能控性的。

[1]张卓.一类时滞边界反馈控制系统的适定性和稳定性研究[J].太原师范学院学报：自然科学版,2010(4)：34-36.

[2]周华成,寇春海.Euler-Bernoulli梁方程基于边界分数阶导数反馈控制的镇定[J].应用数学与计算数学学报,2015,29(2)：211-221.

[3]蔡国平,陈龙祥.时滞反馈控制的若干问题[J].力学进展,2013,43(1)：21-28.

〔责任编辑 高海〕

The Exact Controllability of the System with Small Delays in the Boundary Feedback Controls

ZHANG Zhuo，YANG Chen
(Basic Course Department,Business College of Shanxi University,Taiyuan Shanxi,030031)

In this paper,we mainly consider the beam systems with small delays in boundary feedback controls and boundary condition.Firstly,we formulate the systems as the state feedback control systems on the suitable Hilbert space H.Then we prove that B is admissible.In the end we prove that the system isn't exactly controllable on the state linear space M.

delay;boundary feed back;exact controllability

O175.21

A

1674-0874(2016)03-0020-04

2016-03-10

山西省自然基金资助项目[2013011003-3]

张卓(1983-)，女，山西太原人，硕士，讲师，研究方向：运筹学与控制论。