线性变换关于向量的指数

林大华,戴立辉

（闽江学院数学系，福建福州350108）

线性变换关于向量的指数

林大华,戴立辉

（闽江学院数学系，福建福州350108）

引入线性变换关于向量的指数概念，并对其进行探讨，得到了若干结论。通过线性变换关于向量的指数，刻画了幂幺线性变换的等价条件。

线性变换；向量；指数

线性空间的线性变换的某个幂为恒等变换时，称为幂幺线性变换。线性空间中的每一个向量，在幂幺线性变换的某个幂的作用下不变。根据线性变换与矩阵的关系，幂幺线性变换与幂幺矩阵一样有许多很好的性质，关于它们的研究结果也较为丰富[1-2]。

讨论较幂幺线性变换条件弱一些的线性变换，即线性变换的某个幂仅对线性空间中的某个向量作用时不变，由此引入线性变换关于向量的指数概念，并对其进行探讨。通过对线性变换关于向量指数的研究，刻画了幂幺线性变换的等价条件。

若无特别说明，所涉及到的数均为正整数。用Z表示整数集合，用a|b表示正整数a整除正整数b，[a1,a2,…,an]表示正整数a1,a2,…,an的最小公倍数。其他记号见文献[3]。

定义1设σ是数域F上线性空间V的线性变换，若对α∈V，存在最小正整数k，使得σk(α)=α，则称σ关于α的指数为k，否则称σ关于α的指数为∞。

用zσ(α)表示σ关于α的指数，用Zσ(α)＜∞ 表示σ关于α的指数为有限正整数。

显然，V的恒等变换1V关于V的任一个向量的指数都为1。而V的任意线性变换关于V的零向量指数都为1。

定理1设σ是数域F上线性空间V的线性变换，α∈V。σk(α)=α，则zσ(α)=k⇔ 由σm(α)=α，可推出k|m。

证明 (⇒)设m=pk+r(0≤r＜k),

若r≠0，则α=σm(α)=σpk+r(α)=σr(σpk(α))=

这与zσ(α)=k＞r矛盾，所以r=0，于是k|m。

(⇐)因为σk(α)=α，所以Zσ(α)=t≤k,且由必要性有t|k。另一方面由σt(α)=α及条件有k|t，故zσ(α)=t=k。

推论1设σ是数域F上线性空间V的线性变换，α,β∈V，则

（1）当zσ(α)=k时，有σm(α)=α⇔k|m;

（2）对k(≠0)∈F，有zσ(kα)=zσ(α)；

（3）当zσ(α)＜∞ ,zσ(β)＜∞ 时，有 |zσ(α+β)zσ(α)zσ(β);

（4）当zσ(α)=a,zσ(β)=b且 (a,b)=1 时 ，有zσ(a+b)=ab。

证明（1）(⇒)由定理1的必要性可得。

(⇐)由条件可设m=pk，于是有

（2）当zσ(α)=∞时，若zσ(kα)=m＜∞,

则有kσm(α)=σm(kα)=kσ,

于是由k≠0，有σm(α)=α，这与zσ(α)=∞,

矛盾，故zσ(kα)=∞=zσ(α)。

当zσ(α)=m＜∞时，有σm(α)=α，

于是σm(kα)=kσm(α)=kα，所以zσ(kα)=n＜∞且由定理1可得n|m。 另一方面，由kσn(α)=σn(kα)=kα及k≠0有σn(α)=α，于是由定理1可得m|n，故n=m，即zσ(kα)=zσ(α);

（3）设zσ(α)=a,zσ(β)=b，则σa(α)=α,σb(β)=β，于 是σab(α+β)=σab(α)+σab(β)=α+β,所以zσ(α+β)|ab，即zσ(α+β)|zσ(α)zσ(β);

（4）设zσ(α+β)=m，则由（3）可知m|ab。另一方面，由α+β=σam(α+β)=σam(α)+σam(β)=α+σam(β)可得σam(β)=β，于是b|am，从而由 (a,b)=1得b|m。

同样可得a|m。再由(a,b)=1得ab|m。

故m=ab，即zσ(α+β)=ab。

推论2设σ是数域F上线性空间V的线性变换，则集合Vσ={α∈V|zσ(α)＜∞}是σ的不变子空间。

证明 首先，由zσ(0)=1可知0∈Vσ，所以Vσ是V的非空子集。

其次，∀α,β∈Vσ, ∀k∈P，有zσ(α)＜∞,zσ(β)＜∞，于是由推论1的（2）（3）有

从而kα∈Vσ，α+β∈Vσ。

第三，∀α∈Vσ，设Zσ(α)=k＜∞，则

当k=1 时，由σ(α)=α有σ(σ(α))=σ(α)，于是Zσ(σ(α))=1，所以σ(α)∈Vσ。

当k＞1时，由σk(α)=α有σk-1(σ(α))=σk(α)=α,

于是Zσ(σ(α))≤k-1，所以σ(α)∈Vσ。

故Vσ是σ的不变子空间。

推论3设σ是数域F上线性空间V的可逆线性变换，α∈V，则

（1）当zσ(α)=k时，有σm(α)=σn(α)⇔k|(m-n);

（2）zσ-1

(α)=zσ(α)。

证明（1）由推论1可得

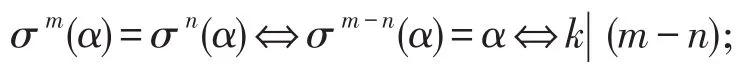
（2）若zσ(α)=∞ ，则 对 任 意 正 整 数m有σm(α)≠α，于 是 有(σ-1)m(α)≠α,所 以zσ-1(α)=∞=zσ(α)。

若zσ(α)=k，则σk(α)=α，于是 (σ-1)k(α)=α，所以zσ-1(α)=m＜∞ 且m|k。

另一方面，由 (σ-1)m(α)=α可得σm(α)=α，从而k|m。故m=k，即zσ-1(α)=zσ(α)。

推论4设数域F上线性空间V的线性变换σ关于α∈V的指数为k，则

（1）对任意正整数m，都存在小于k的非负整数r，使得σm(α)=σr(α);

（2）当 0≤p≠q＜k时，有σp(α)≠σq(α)；

（3）Sα={σm(α)|m∈Z,m＞0}={α,σ(α),σ2(α),…,σk-1(α)}。

证明（1）由定理1的必要性证明可得；

（2）不妨设p＜q，若σp(α)=σq(α)，

则有α=σk(α)=σ(k-p)+p(α)=σk-pσp(α)=σk-pσq(α)=σk-(q-p)(α)，

因为 0≤p＜q＜k，所以0＜k-(q-p)＜k，这与Zσ(α)=k矛盾，故σp(α)≠σq(α)；

（3）由（1）和（2）可得。

定理2设σ是数域F上线性空间V的线性变换，α,β∈V且Zσ(α)=k,Zσ(β)=l，若存在正整数p,q，使得σp(α)=σq(β)，则k=l。

证明 由推论4，可不妨设0≤p＜k,0≤q＜l，

因为σp(α)=σq(β)，所以α=σ(k-p)+p(α)=σ(k-p)+q(β)，β=σ(l-q)+q(β)=σ(l-q)+p(α)，

于是对任意正整数m，有σm(α)=σm+(k-p)+q(β)∈Sβ，σm(β)=σm+(l-q)+p(α)∈Sα，

从而Sα=Sβ，故由推论4中的（3）可得k=l。

推论5设σ是数域F上线性空间V的线性变换，α,β∈V且Zσ(α)＜∞,Zσ(β)＜∞，

若Zσ(α)≠Zσ(β)，则对任意正整数p,q，都有σp(α)≠σq(β)。

定理3设σ是数域F上n维线性空间V的线性变换，α1,α2,…,αn是V的一个基，则zσ(αi)＜∞(i=1,2,…,n)，

⇔σ是幂幺线性变换，且σ的幂幺指数（使σm=1V成立的最小正整数m）是[zσ(α1),zσ(α2),…,zσ(αn)]。

证明 (⇐)因为σ是幂幺线性变换，所以存在正整数m，使得σm=1V，从而有σm(αi)=αi(i=1,2,…,n)

故zσ(αi)＜∞(i=1,2,…,n)。

(⇒)令

zσ(αi)=ki(i=1,2,…,n)，k=[k1,k2,…,kn]

则由ki|k(i=1,2,…,n)，有σk(αi)=αi(i=1,2,…,n)。

于是∀α∈V，由

所以σk=1V，故σ是幂幺线性变换。

设σ的幂幺指数为m，则由σk=1V有m|k。

事实上，设k=pm+r(0≤r＜m)，若r≠0，则∀α∈V，有α=σk(α)=σpm+r(α)=

即σr=1V，这与σ的幂幺指数为m＞r矛盾，所以r=0，故m|k。

另一方面，由σm=1V，有σm(αi)=αi(i=1,2,…,n)，

于是ki|m(i=1,2,…,n)，从而k|m，故m=k，即m=[k1,k2, … ,kn]=[zσ(α1),zσ(α2),…,zσ(αn)]。

[1]唐建国,严青云.幂幺矩阵的充要条件[J].数学的实践与认识,2010，40（20）：172-176.

[2]林大华,戴立辉.幂幺矩阵的幂幺指数[J].数学的实践与认识,2012，42（18）：252-255.

[3]北京大学数学系几何与代数教研室前代数小组.高等代数(第三版)[M].北京：高等教育出版社，2003.

〔责任编辑 高海〕

Index of Linear Transformation on Vector

LIN Da-hua,DAI Li-hui
(Department of Mathematics,Minjiang University,Fuzhou Fujian,350108)

In this paper,we introduced and study the index of linear transformation on vector.We obtained some results of it and characterize some equivalent conditions of unipotent linear transformation.

linear transformation;vector;index.

O151.2

A

1674-0874(2016)03-0010-02

2016-03-10

福建省中青年教师教育科研项目[JB13164];闽江学院教育教学改革研究项目[MJUB2013033]

林大华（1959-），男，福建福州人，副教授，研究方向：代数学。