多维剖析“探”解法多重境界“究”推广

☉四川省苍溪中学　校李波

多维剖析“探”解法多重境界“究”推广

☉四川省苍溪中学校李波

每一年高考结束后，总会留下许多经典杰作供一线教师研读与品味.2016年高考数学四川卷注重传统的继承发扬和创新，在保留四川卷特色的同时，有意识地向全国卷靠拢，平稳过渡的特点相当鲜明.“突出考查数学基础知识、主干知识、基本数学方法和数学思想以及数学品质.”；同时试题也注重文化背景，引用了《数书九章》中的秦九韶算法；注重实际应用，将数学考查与社会生活紧密结合，如应用题的水资源问题.试卷的起点较低，出口较高，梯度比较明显，试卷的区分度非常好.

笔者特别关注了四川卷理科的第8题，不难发现，该题考查了考生对抛物线的性质、参数方程、三角形的重心公式、向量线性运算等知识的综合运用.立足于基础，注重技能和知识交汇的考查，凸显高考对能力的要求.本文从多个视角给出不同解法，并对该问题进行多层次的推广，如有不妥之处，还望同行批评指正.

【题目】设O为坐标原点，P是以F为焦点的抛物线y2= 2px（p>0）上任意一点，M是线段PF上的点，且|PM|=2|MF|，则直线OM的斜率的最大值为（）

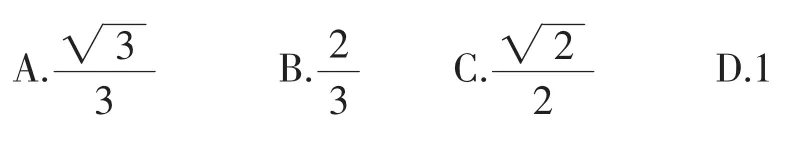
【答案】C

视角一、直译

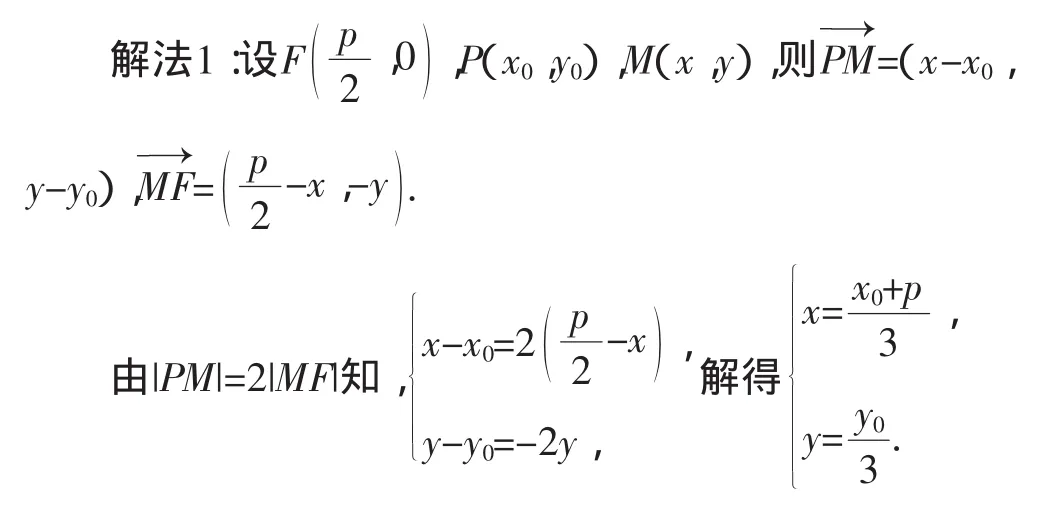
评析：在处理数学问题时，最常用的方法是直译法，即将题干中的已知条件直接代数化，需要注意的是，该方法“少想多算”，这与近几年高考题的命题特点是不相符的，因此，在平常教学中指导学生还是以“多算少想”为主.

上述解法1中，将x，y分别用x0，y0表示，得到的斜率表达式为，显然求该式的最大值直接考虑均值不等式；如果将x0，y0分别用x，y表示，得到的斜率表达式又是怎样？求其最值又该用什么方法？

视角二、函数思想

评析：利用函数单调性求最值是处理最值问题常用方法，简单易于操作，本题中采用代入消元法将目标函数由二元化为一元，从而将问题转化为一元函数求最值.解析几何中求最值常用的方法有：均值不等式、配方法、构造函数利用单调性求最值.

视角三、参数方程

解法4：设P（2pt2，2pt），M（x，y）（不妨设t＞0），则，由题易知解得所以M点坐标为），所以直线OM的斜率为当且仅当，即P点坐标为时，直线OM的斜率有最大值，故选C.

评析：针对点在圆锥曲线上的最值问题，可以考虑参数法，将坐标中两个变量化为一个变量，方便在求最值时使用均值不等式、配方、构造函数判断单调性.

视角四、平面几何性质

解法5：如图1，过P、M点分别作x轴垂线交x轴于Q、N两点，设P（x0，y0），易知△MFN与△PFQ相似.

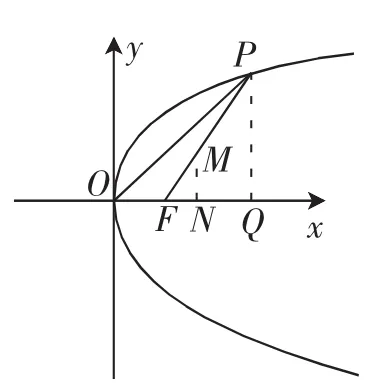
图1　

评析：“以形解题”是解决数学问题重要的思想方法，善于利用图形中的几何关系实现量与量之间的转化，从而简化计算过程，提高解题质量.

三角形重心是三角形三边中线的交点.性质比例为重心到顶点与到对边中点比为2∶1.本题中P、M、F三点共线，|PM|∶|MF|=2∶1.为此很容易联想到点M为三角形的重心.不妨在x轴在取一点Q（p，0），连接线段PQ，此时点M刚好为三角形△POQ的重心，从而引出解法6.

视角五、三角形重心的性质

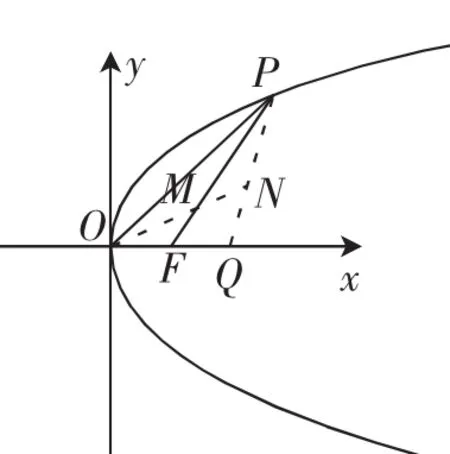
图2　

视角六、三角形重心公式

评析：“数形结合”的思想是高中阶段重要的数学思想，不少代数问题都有其几何背景.挖掘这些几何特征，“以形助数”能让问题的解决更直观简捷，也体现了命题人“多一点想，少一点算”的指导思想.笔者认为运用“数形结合”解决本题是高屋建瓴，拨开云雾的一种彻底理解题意的方法.

视角七、抛物线的定义法

解法8：如图1，在△OFP中，设|PF|=m，∠OFP=θ，θ∈（0，π），则|PQ|=msinθ，|FQ|=mcosθ，由|PM|=2|MF|知，|MN|=

即直线OM的斜率有最大值kOM=

图3　

视角八、向量的线性运算

【一般结论】

推广1设O为坐标原点，P是抛物线y2=2px（p>0）上任意一点，F（m，0）（m>0），M是线段PF上的点，且|PM|= 2|MF|，则直线OM斜率的最大值

证明：由题知，设P（x0，y0），则向量），即M点坐标为，由P（x0，y0）在抛物线上知当且仅当，直线OM的斜率有最大

说明：当点M为直角三角形的重心时，直线OM的斜率有最大值.

推广2设O为坐标原点，P是抛物线y2=2px（p>0）上任意一点，T（t，0），F（m，0），M是线段PF上的点，且|PM|= 2|MF|.

（1）若2m-3t≤0，则直线TM斜率无最值；

推广3设O为坐标原点，P是抛物线y2=2px（p>0）上任意一点，T（t，0），F（m，0），M是线段PF上的点，且|PM|= λ|MF|.

（1）若mλ-（λ+1）t≤0，则直线TM斜率无最值；

（2）若mλ-（λ+1）t>0，则直线TM斜率的最大值

推广4设O为坐标原点，P是抛物线y2=2px（p>0）上任意一点，T（0，t），F（0，m），M是线段PF上的点，且|PM|= λ|MF|.

（1）若mλ-（λ+1）t=0，则直线TM斜率无最值；

（2）若mλ-（λ+1）t>0，则直线TM斜率的最小值

（3）若mλ-（λ+1）t<0，则直线TM斜率的最大值

推广2、3、4的证明同推广1，在此就不在论述.

证明：由题知，设P（x0，y0），则向量，即M点坐标为

证明同推论5.

高考题是命题组集体智慧的结晶，高中一线教师在教学的过程中，应该充分利用高考题素材，潜心研究高考题，对高考题一题多解、多视角探究、变式、延伸，剖析其本质、背景.教师要有进行教育所需的扎实而宽厚的基础知识、专业知识以及研究能力，只有这样学生才能让跳出题海，一眼看透题、一题串一题，一题变多题.

1.周国溢.一道调研试题的多视角求解［J］.中学数学（上），2015（2）.