有效建构模型 凸显数学知识的本质——基于“小数意义”教学的一点思考

江苏省南通市如东县掘港镇环镇小学　李雪梅

有效建构模型凸显数学知识的本质——基于“小数意义”教学的一点思考

江苏省南通市如东县掘港镇环镇小学李雪梅

数学从内在的知识本身的特点来看，具有高度抽象和概括的特征。这一特征决定了数学的发展是一个知识的框架的构建过程。任何一个最简单的数学问题和数学对象，都是通过人类抽象思维，最后概括的结果。数学从开始的原始的概念，通过几个原始的概念再一次深化为抽象的另一个更具抽象的概念，数学的概念和逻辑关系，就是通过这样的不断地抽象和概括，就建立了数学的知识框架和网络。每一个人在学习数学的时候，主要是看对数学的理解是否知道知识内在的联系和抽象的关系，能否形成自己的知识框架，自己建立的知识框架是否科学和合理。对每一个学习数学的人来说，这是决定能否学好数学的关键。

教学小数的意义，典型的教法莫过于，让学生通过对生活实例的观察、比较以及操作等各种活动，然后抽象概括，得出“十分之几写成一位小数，百分之几写成两位小数，千分之几写成三位小数……”的结论。好多教师认为这样的教学是圆满的，但实际上学生对知识的认识是肤浅的，没有深度和厚度。这样的教学只关注了生活意义，没有知识的框架和知识间的网络，只有生活经验唤醒，没有理性总结；活动味过度，只有活动操作，没有回顾、思索、提炼。学生通过实例观察比较和画图操作等这些方式得出结论，都无可厚非，但这只是一种合情的归纳推理，没有深入问题的本质，“小数”的模型并没有真正在学生的脑子里建立起来。由于这一基本概念没有打牢，在后面的教学中学生出现各种理解上的错误也就可想而知了。只有深入知识的本质和来源，才能有效建立起数学模型。

究其原因，是教师对小数的意义缺乏最本真的理解，没有从数学的视界考虑教学问题。让我们先来看看小数的本质意义是什么。上网百度一下，我们就会知道：小数本质上是一种特殊的分数，即十进制分数。十进制分数是根据十进制的位值原则，把十进分数仿照整数的写法写成不带分母的形式，即分母是10n的（n为自然数）分数叫作“十进制分数”。任何一个“十进制分数”都能写成小数的形式，如7/10=0.7，7/100=0.07，等等。剖析它的本质意义，我们会发现这样一种知识框架：十进制分数和小数有着密切的联系，它们意义相同，只是形式不同，“意义”和“形式”是我们教学小数意义的关键词，所以在教学中我们不仅要让学生明白小数的意义，还要让学生理解怎样实现一种形式到另一种形式的转换。基于这样的认识，我们的教学就有了明确的目标：第一，使学生借助直观认识小数的意义，能理解小数和分数的联系，能根据分数写出相应的小数；第二，使学生在认识小数意义的过程中，体会数学知识之间的联系和数的扩展，培养观察比较、综合归纳和抽象概括等思维能力，进一步发展数感；第三，使学生主动思考，体会数的不同表示方式，产生对数的表达方式的兴趣。我们的教学思路就变得清晰而简单了，教师也很容易把握教学的重点和难点。因此典型的教法可以做以下的改进：

首先，通过生活实例让学生充分体会十进制分数的实际意义。例如，1厘米是1米的1/100，是1/100米；4厘米是1米的4/100，是4/100米；12厘米是1米的12/100，是12/100米。然后告诉学生：这样的分数还可以写成小数的形式：1/100米=0.01米；4/100米=0.04米；12/100米=0.12米。引导：这里都是几位小数？（两位）怎样的分数可以写成两位小数？（百分之几写成两位小数）

接着，还要让学生理解我们是怎样把百分之几转换成两位小数的，这是小数最本质的特征之一，也是很多教师在教学中疏忽的地方，这一部分教学可以这样板书：

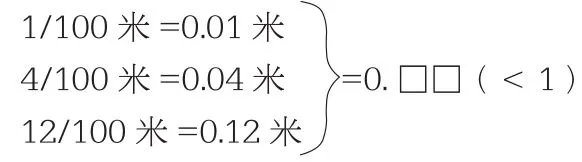
根据以上板书进行引导：在不满整数“1”的情况下，你有没有发现小数部分的数就是原来分数的什么？（分子）在不满整数“1”的情况下，分子最少是一位数，最多是两位数，所以百分之几写成两位小数。当分子是一位数的时候，把分子写在小数部分的第二位上，小数部分第一位添0占位；分子是两位数的时候，就把分子直接写在小数部分。

同理，（）=0.□□□（在不满整数“1”的情况下），分子最少是一位数，最多是三位数，所以千分之几写成三位小数。分子是一位数的时候，把分子写在小数部分第三位上，小数部分第一、二位都写0，分子是两位数的时候，就把分子写在小数部分的第二、三位，第一位写0，分子是三位数的时候，就把分子直接写在小数部分。通过这样的教学让学生体会小数是一种特殊的分数（即分子是10、100、1000……的分数），这种分数和小数只是形式不同而已，其实本质上是一致的，这一点特别重要。这样学生才能真正建立起“小数”的模型。对于一个学生来说，当一个学生明白了数学知识的本质，才能够通过学习建立合理的知识框架、合理的知识脉络。在学生每学完一阶段知识的时候，学生才能够自觉地梳理知识，构建知识框架。

这个例子都告诉我们，小学数学教学常常借用一些日常生活经验来表征数学概念，这无可厚非。如果仅仅习惯性地、直白地从生活意义去解读这些概念，所教数学概念的内涵就不那么深刻，就会发生偏差。这样，学生对数学概念掌握不牢靠也就成了必然的事情。而如果教师能有意识地让这些生活经验回归数学科学的本体，考究这些生活实例的数学意义，并适当利用这些实例的生活意义，那么设计的教学就完全有可能达到一种完美：既充分利用了学生的生活经验，又超越了经验层面，提升为初步理性的认识。

数学教学既需要上位的教育学、心理学一般教育理论的指导，更应该寻求以数学视野为基点的各种理性认识的指导。要提升课堂的教学效果和效率，需要教师对数学概念的精准理解，对数学思想方法的把握，对数学思维方式的运用。我们的数学教学就是要具体中见理性，浅显中见深刻，直白中见经典，这样才能凸显知识的本质，有效建构模型，彰显数学的魅力。