“绝对值”教学设计

江苏省淮安市淮阴区渔沟中学　吴　艳

“绝对值”教学设计

江苏省淮安市淮阴区渔沟中学吴艳

一、教学内容分析

绝对值问题是中学数学的一个重点和难点内容，也是高考的一个热点内容。绝对值内容贯穿整个中学数学教材，初中数学主要研究以绝对值的代数意义解决各种绝对值问题，本节课渗透着“分类讨论”和“数形结合”的重要数学思想，是初入初中的重要一课。

二、学生学习情况分析

学生数学钻研的精神相差较大，所以可适当对知识点进行拓展。中低等程度的学生占大多数，程度较高的学生占少数。学生之前已经学习了数轴，在已有的知识经验基础上学习，学生更容易参与其中。

三、设计思想

注重各个层面的学生，启发诱导式培养学生学会学习、学会探究是全面发展学生能力的重要前提，是初中新课程改革的主要任务。让学生在一定的情境中，运用已有的学习经验，并通过与他人（在教师指导和学习伙伴的帮助下）协作，主动建构而获得知识。

四、教学目标

1.知识与能力

①使学生掌握绝对值的概念及表示方法。

②使学生熟练掌握绝对值的求法和有关绝对值的计算问题。

③了解绝对值的几何意义，特别的，会用绝对值比较两个负数的大小。

2.过程与方法

自主学习，发现问题，解决问题。

3.情感态度与价值观

经历将实际问题数学化的过程，感受数学与生活的关系。

五、教学重点难点：正确理解绝对值的意义

六、教法与学法：教师讲授引导，学生小组交流、合作探究。

七、教学程序设计

（一）知识准备

1.在数轴上表示+2的点B在原点的______边，它与原点的距离为______个单位长度；表示-3的点A在原点的______边，它与原点的距离______个单位长度；表示+2的点在表示-3的点____边，它们之间的距离______个单位长度。

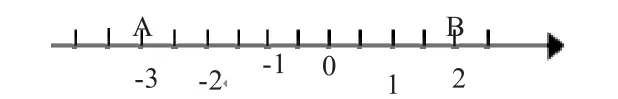
2.用“＞”或“＜”填空：

（1）-5____0（2）-7____-9（3）5____-10

（4）-4____4

（二）合作探究

【活动一】概念探究

在数轴上，表示+2的点与原点的距离是______，表示-3的点与原点的距离是______，表示0的点与原点的距离是______。

1.数轴上表示一个数的点与原点的距离，叫作这个数的绝对值

例如，表示-3的点与原点的距离是3个长度单位，所以-3的绝对值就是3。

表示3的点与原点的距离是3个长度单位，所以3的绝对值就是3。

表示0的点（原点）与原点的距离是0，所以0的绝对值就是0。

2.表示方法

通过上面的讨论我们知道3的绝对值是3，而—4的绝对值是4，那么它们的写法如下：

|3|=3；读作“3的绝对值”，|-4|=4；读作“-4的绝对值”。

3.自主练习

说出并写出数轴上A，B，C，D，E各点处的数所表示的绝对值。

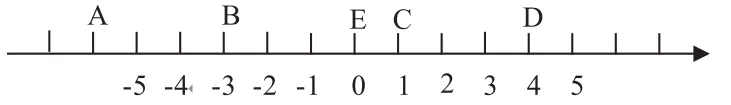
【活动二】绝对值的相关应用

例1求|4|、|-3.5|的值。

求有理数的绝对值，一般用代数意义求解，即正数的绝对值等于它本身，负数的绝对值等于它的相反数，0的绝对值是0。

例2比较－3与－6的绝对值的大小。

两个有理数比较大小时，首先要判断这两个数是正数、负数，还是零，然后再根据有关判定方法进行判定。借助数轴也可以比较大小，但用绝对值的方法更方便。

例3在数轴上表示各数，并写出它们的绝对值，-3，+2.5，－1，3.2，0。

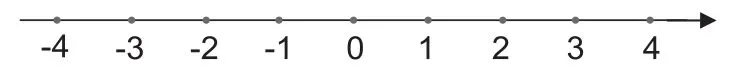
讨论：

（1）0有没有绝对值？如果有是多少，为什么？

（2）有理数绝对值的计算有没有什么规律可循？

排序：

（1）把原来的5个数按从小到大顺序排列：（）。

（2）把它们的绝对值按从小到大顺序排列：（）。

【活动三】展示交流

1.绝对值等于5的数是______；

2.绝对值小于5的整数有______；

3.绝对值大于1.5而小于4的整数有______；

4.|x|=9，则x=______；|y—3|=0，则y=______；

5.比赛中使用乒乓球的重量是有严格规定的。检查5只乒乓球的重量，超过规定重量的毫克数记作正数，不足规定重量的毫克数记作负数，检查结果如下：（）。

请指出哪只乒乓球的质量好一些？你能用绝对值的知识进行说明吗？

（三）课堂小结

本节课你有何收获？

（四）当堂达标

1.比较大小

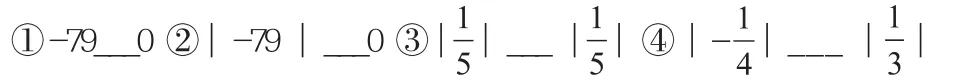
2.计算

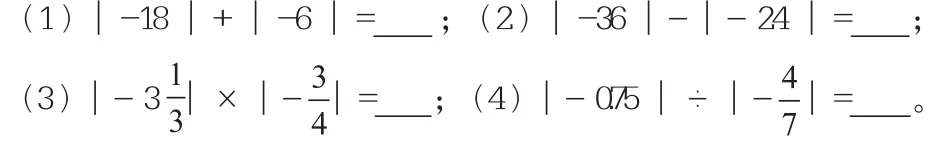
3.绝对值小于3的整数有________。

4.绝对值不大于4的非负整数有________。

5.绝对值大于2而小于5的整数有________。

6.把下列各数填入相应的集合里.

整数集合：｛｝；正数集合：｛｝；分数集合：｛｝。

（五）作业布置

完成课后作业

八、板书设计（略）

九、教学反思

1.让探究式教学走进课堂为学生的学习提供了多样化的活动方式，激发学生的兴趣，让学生积极参与。学生通过观察、猜想、推理等丰富多彩的活动达到了知识的主动构建与理解。

2.这些年数学给我们孩子们留下了什么？我想应该是学生遇到具体问题时那种思考问题的方式和解决问题的方法。华罗庚先生曾说：“数缺形时少直观，形缺数时难入微。”在引导学生观察图形后研究问题，要注意渗透数学思想方法的教学。