灵动的思维——几何直观在“数学广角”教学中的应用探析

广东省东莞市东城第三小学　李平龙

灵动的思维——几何直观在“数学广角”教学中的应用探析

广东省东莞市东城第三小学李平龙

“数学广角”是小学数学教学中一个非常重要的教学内容，它把重要的数学思想方法通过学生可以理解的、有趣的、容易接受的生活问题呈现出来，使学生通过观察、操作、实验、猜测、推理与交流等活动，初步感受数学思想方法的奇妙与作用，受到数学思维的训练，逐步形成有序地、严密地思考问题的意识。因此，通过在数学广角中的教学，使学生感受数学思想方法，提高他们的数学思维能力是重要的教学目标。在教学中我发现一部分学生对数学广角中的数学思想、思维过程感觉深奥难懂，任凭老师讲得口干舌燥，学生仍难以理解，最后教师只能无奈地放弃过程，直奔结果。学生只能是死记硬背老师总结出来的公式或规律，生搬硬套地解决问题。有感于此，我在近两年的教学中尝试着利用几何直观的方法来突破这个难点。“几何直观”是指利用图形描述和分析数学问题，探索解决问题的思路、预测结果。弗赖登塔尔说：“几何直观可以告诉我们什么是重要的、有趣的和容易进入的，当我们陷入问题、观念、方法的困扰时，几何可以拯救我们。”借助几何直观可以把复杂的数学问题变得简明、形象，促进数学的理解；通过对实物和图形进行观察，有利于信息提取和方法的促成；根据直观认识来研究图形的性质和相关问题有助于数学问题结构的揭示。

以下就结合近两年所上的数学广角的“找次品”“鸡兔同笼”“植树问题”“排列与组合”等课例反思几何直观在数学广角教学中的应用。

一、利用几何直观建立数学模型——启迪思维，帮助理解

当一个问题需要用数学方法来思考时，有时用几何方法能够最快最有效地解决，这也是几何直观的作用。

例如，在教学五年级“找次品”时，为了让学生理解用天平称一次就能从3瓶口香糖中找出少了3粒的那瓶。我拿出了一个天平放在讲台上，先拿两瓶上去称。

师：平衡吗？哪瓶少了3粒？

生1：不平衡。翘起来的那瓶少了3粒。

师：如果运气差一点呢（把少了3粒的那瓶换成另外一瓶）？平衡吗？哪瓶少了3粒？

生2：平衡，剩下没称的那瓶就少了3粒。因此，只要一次就能找出。

我利用天平称给学生看，这种最直观的方式让学生看到平衡和不平衡两种情况，然后在课件中用图示直观地呈现出来。在这个过程中，天平已经从实物抽象成了简图，口香糖的实物也抽象成了图片。实物称能让学生看到具体的数学模型，课件中的图片直观有利于学生思考和对比（图1）。

图1

从3瓶中找出较重或较轻的次品，其中渗透了排除的数学思想，这种数学思想在日常生活中有着广泛的应用，这既是学习本课的起点，又是学生需要理解的重要知识。以往自己上课或别的老师上课时，一般没有呈现用天平称的过程，而只是让学生通过模拟、画图、口头描述等来进行解释，在教学中我发现有些学生特别是学困生理解或解释起来很费劲。而这些困难的产生的根源就在于学生没有见到真正的实物模型，只是凭空想象，因此，我把天平实物引入了这节课的教学，这样的问题就迎刃而解了。

《数学课程标准》在教材编写建议中明确提出：“根据学生已有经验、心理发展规律以及所学内容的特点，一些重要的数学概念与数学思想应采用逐步渗透、深化、螺旋上升的方式编排。”人教版实验教材在编排“数学广角”时，主要是通过一些比较简单的事例渗透一些重要的数学思想方法，让学生在解决问题的过程中尝试从数学的角度寻求解决问题的策略，经历猜想、实验、推理等数学探索活动的过程，体会一些重要的数学思想方法。而在教学中，利用几何直观帮助学生逐步实现从感性思维向理性思维的过渡是必不可少的。

例如，在教学“找次品”时，我设计了四个层次的几何直观方式，

首先，利用天平称给学生看，这种最直观的方式让学生看到平衡和不平衡两种情况，然后在课件中用图示直观呈现出来（图2）。在这个过程中，天平已经从实物抽象成了简图，口香糖的实物也抽象成了图片。实物称能让学生看到具体的数学模型，课件中的图片直观有利于学生思考和对比。

图2

接着，学生从5个物品中找出较轻的次品时，我让学生用小圆片摆一摆。刚才的实物图片被小圆片所代替，箭头图则直观地呈现分的份数和每份的数量。

然后，在学生从9个物品中找出较重的一个次品时，手中的圆片已经不够用了，我把黑板上的圆片一边取下（图3），一边换成数字（图4），图示如下：

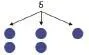
图3

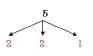
图4

最后，整节课的板书（图5）如下：

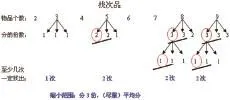
图5

在整节课的过程中，我利用不同的几何直观方式进行了巧妙的递进，先利用天平直接称口香糖（实物），然后利用圆片摆一摆（初步模型），再用数字代替圆片（数字模型），最后形成整个板书图（数形结合），引导学生经历了从实物—圆片—数字—文字的过程。极大地帮助了学生理解知识，在经历建模过程的同时启迪了学生的思维，提高了思维能力。

二、利用几何直观呈现思维过程——直观有序，深刻理解

恰当的几何直观方式能有效地呈现思维的过程，让学生清楚地理解思维的过程，这样对学生的思维能力培养起到积极的作用。

例如，在教学二年级“排列组合”时，有这样一个问题：用1，2，3能组成几个两位数。在听我们学校一位老师上课时，她向学生渗透的方法是（图6）：先在黑板上写好个位、十位，然后在下面依次去写数字，组成六个两位数，然后让学生说一说组数的过程和顺序，大部分学生都能掌握。

图6

但我在听课的过程中发现，有部分学生会出现重复或遗漏的情况。在我们成人的眼里看来，这样已经讲解得非常清楚了，为什么会出现这样的情况呢？通过分析发现，虽说这位老师也是采用了几何直观的方式让学生理解这部分知识，但更注重于结果的呈现，无法反映思维的过程。究其原因有两点：一是二年级孩子的思维水平是比较低的，我们成人觉得十分简单的过程在他们眼中并不简单，因此不能用我们成人的思维来类推他们的思维，二是在孩子们的眼中这样的图还不够直观，特别是这个图不能直观地反映“取数”的顺序和“组数”的过程。后来在教学中我采用另一种几何直观的图示来尝试解决这个问题。

结合板书，让孩子们边画边说（图7），先取1，剩下2和3，能组成12和13；再取2，剩下1和3，能组成21和23；最后取3，剩下1和2，能组成31和32。

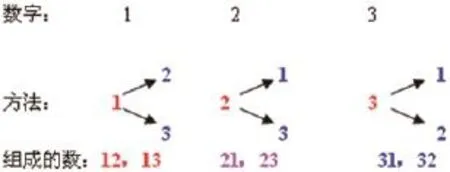
图7

课后发现，所教二（5）班的48个孩子不仅很喜欢这种直观画图的方式，而且都掌握了组数的方法，在后面的练习中极少出错。因此，通过恰当的几何直观的方法，能直观呈现思维的过程，帮助学生深刻地理解思维的过程。

三、利用几何直观启迪学生思考——数形结合，提炼总结

只有做到直观上的理解，才是真正的理解。几何直观能够启迪思考，帮助理解，因此，在日常教学中，要帮助学生借助几何直观进行思考，揭示研究对象的性质和关系，并且学会利用几何直观来学习和理解数学。

在“找次品”一课中，为了让学生理解“分3份”“尽量平均分”这两个规律，我先引导学生尝试从9个物品中找出较重的一个次品，画出示意图，然后把学生的方法呈现成以下几何直观图（图8）：

教学实录如下：

师：为什么都是分3份，但找到次品需要称的次数却不相同？（在借班上课时学生没有答出，我就追问，哪种方法称一次把范围缩得更小？）

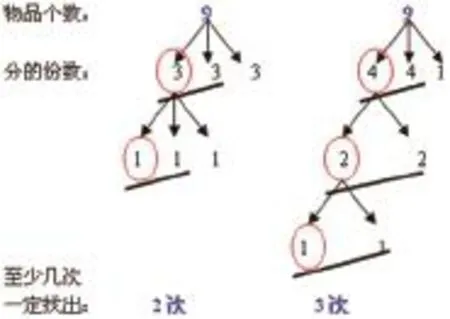
图8

生1：因为缩小的范围不同。第一种方法一次就把范围缩小到了3瓶，第二种方法一次只把范围缩小到了4瓶。

师：那怎样分就更有利于缩小范围呢？

生：平均分。

接着，我让学生从8个物品中找到较重的一个次品。反馈的信息如下（图9）：

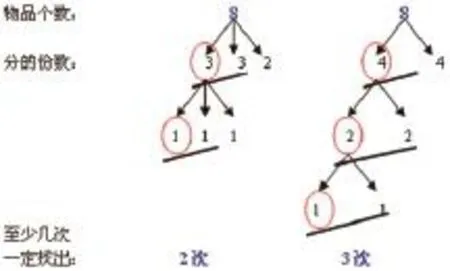
图9

教学实录如下：

教师先让学生讨论为什么第一种方法只要两次，第二种方法却要三次。

生1：因为第一种把范围缩得更小。

师：但第二种却是符合平均分的啊？

生1：因为第一种是分3份的。

生2：分3份更重要，刚才的9就是平均分成3份的。

师：那像8这样不能平均分3份的，怎么办？

生3：尽量吧。

师：没错，尽量平均分。

以上两个片断中，我都充分使用了几何直观的方法，短短的几次问答，就解决了学生理解“分3份”“尽量平均分”这两个找次品问题中潜在的规律，这就是几何直观的威力。上面的两个图巧妙地把数和形结合起来了，利用箭头图呈现分的份数和每份的多少，利用斜线直观地反映不平衡的情况，利用圆圈清楚地标示出称后缩小的范围，而整个图形实现了两种方法的对比。最后再通过恰当的提问引导学生从复杂的信息中找到内在的数学规律和思想。

综上所述，在数学广角甚至整个数学教学中，恰当地采用几何直观的方法进行教学，不仅可以提高学生的思维能力，还可以提高学生的学习兴趣和效率，达到事半功倍的效果。

［1］李军.正确理解“数学广角”编排意义，提高教学有效性［J］.山东教育，2009（31）.

［2］朱洪霞.几何直观在小学数学教学中的作用［J］.新课程（教研版），2009（01）.