DC规划的一些结论及推广
付 裕,马琳晶,李科科
(重庆师范大学,重庆 401331)
DC规划的一些结论及推广
付裕,马琳晶,李科科
(重庆师范大学,重庆 401331)
针对DC(difference of convex)规划,结合最优化理论和算法的相关知识,用不同的方法对DC规划中已有的一些定理和结论进行了证明。在此基础上,对其中一些结论进行了推广,并且阐述了一类DC规划和其对应的反凸规划的最优解之间的联系。最后利用L-次微分等相关知识,提出并讨论了一类特殊DC规划和其相关的一类凸规划的最优解之间的联系与区别。
最优化理论和算法;DC规划;反凸规划;最优解
DC(difference of convex)规划是非凸规划中很重要的一类规划问题,它在经济、管理和工程等领域有着广泛的应用。事实上,许多最优化问题,如不定二次规划[1]、弱凸规划[2]和广义几何规划[3-4]等,都是DC规划问题的特殊形式。许多方面的应用涉及的函数可以表示成2个凸函数的差,此时产生的优化问题可以表示为DC规划,例如聚类分析、选址问题、交通运输规划、多层次规划、多目标规划和工程设计等[5-9]。由于许多数学规划问题都可以转化为DC规划来求解,因此研究DC规划的理论和算法具有重要的理论意义和应用价值。
1 预备知识
定义1[10]定义在凸集X⊆Rn上的实值函数f称为X上的d.c.(或者DC)是指对于所有x∈X,f能表示成

(1)
其中,p,q是X上的凸函数。Rn上的d.c.称为d.c.函数(或者DC函数),式(1)称为f的d.c.分解(或者DC分解)。
定义2[10]全局优化问题称为d.c.规划问题,或者d.c.规划(DC规划),是指它具有如下形式:
(2)
其中X是Rn上的闭凸子集,且所有的函数fi是d.c.函数(i=0,1,…,m)。
不失一般性,令f0(x)=f(x)-g(x),并且对所有的i=1,…,m,令fi(x)=0,那么规划(2)可以转化为如下形式的规划:
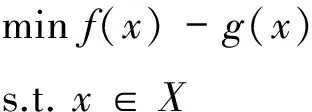
其中: f和g是Rn上的2个凸函数;X是Rn中的闭凸子集。
定义3[10]典范d.c.规划问题是指如下形式的优化问题:
其中c∈Rn,g∶Rn→R上是凸的,并且D是Rn的闭凸子集。
2 DC规划向典范形式的变换
子集F∈Rn称为d.c.集,是指它可以表示为F=DK,其中D和K是Rn中的两个凸集。在文献[10]中,R.Horst和N.V.Thoai给出了如下引理1和引理2,本文给出引理2的详细证明过程。
引理1[10](1)对于每一个集合M={x∈Rn∶di(x)≤0,di(x)是d.c.(i=1,…,m)}有一个d.c.集F∈Rn+1,使得(x,xn+1)∈F⟺x∈M。(2)每个d.c.集F={x∈Rn∶h(x)≤0,g(x)≥0},其中h和g是凸函数,可以描述成如下形式:
其中,函数d(x)是d.c.函数。
引理2[10]Rn中的每个d.c.规划可以转换成1个等价的Rn+2中的典范d.c.规划。
证明因为Rn中的每个形如问题(2)的规划等价于Rn+1中如下形式的规划:
(3)
定义gj(x,xn+1)(j=0,1,…,m)如下:
则规划(3)可写为如下等价形式:
(4)
设M和gj(x,xn+1)分别为:
M={xn+1∈R∶gj(x,xn+1)≤0
j=0,…,m, x∈Rn}
gj(x,xn+1)=pj(x,xn+1)-qj(x,xn+1)
j=0,1,…,m
其中pj和qj均为凸函数,并且令
那么M为
定义凸函数φ(x,xn+1,xn+2)、凸函数ψ(x,xn+1,xn+2) 和d.c.集F分别为:
φ(x,xn+1,xn+2)=p(x,xn+1)-xn+2
ψ(x,xn+1,xn+2)=q(x,xn+1)-xn+2
F={(x,xn+1,xn+2)∈Rn+2∶φ(x,xn+1,xn+2)≤0,
ψ(x,xn+1,xn+2)≥0}
那么,(x,xn+1,xn+2)∈F⟺x∈M成立,即规划(4)等价于规划min{xn+1∈R∶(x,xn+1,xn+2)∈F}。综上所述,引理2得证。
由引理1和引理2以及引理2的证明可得到命题1,该命题是引理2的推广形式。
命题1Rn中的每个d.c.规划可以转换成一个等价的Rn+k(k为正整数)中的典范d.c.规划。
证明由引理2的证明可知Rn中的每个形如问题(2)的规划等价于Rn+1中的形如(3)的规划。
因为规划(3)可以转换成一个与Rn+k中等价的如下形式的规划:
(5)
所以,Rn中的每个形如问题(2)的规划等价于Rn+2中的形如(5)的规划。
定义gj(x,xn+1,xn+2),j=0,1,…,m+1,如下:
那么规划(5)可写为如下等价形式:
(6)
设M和gj(x,xn+1)分别为:
其中pj和qj均为凸函数,并且令
那么M为
分别定义凸函数φ(x,xn+1,xn+2,xn+3)、凸函数ψ(x,xn+1,xn+2,xn+3)和d.c.集F如下:
那么(x,xn+1,xn+2,xn+3)∈F⟺x∈M成立,即规划(6)等价于规划
以此类推可得:Rn中的每个d.c.规划可以转换成一个等价的Rn+k(k为正整数)中的典范d.c.规划。
3 一类DC规划和反凸规划
考虑如下形式的DC规划:

其中:f和g是Rn上的2个凸函数;X是Rn内的闭凸子集。
利用1个辅助变量t(∈R),定义如下规划:
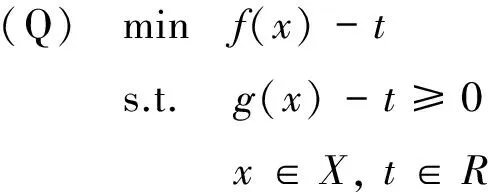
规划(Q)称为反凸规划[11]。
R.Horst和N.V.Thoai在文献[9]中给出了引理3,本文给出引理3的证明过程。
引理3[1]x*∈X是规划(P)的一个最优解,当且仅当存在t*∈R,使得(x*,t*)为规划(Q)的一个最优解。
证明
1) 充分性。因为x*∈X是规划(P)的一个最优解,所以对任意的x∈X有不等式 f(x*)-g(x*)≤f(x)-g(x)成立。令t*=g(x*),则对所有满足条件t≤g(x)的x(∈X)和t(∈R)有不等式 f(x)-t≥f(x)-g(x)≥f(x*)-g(x*)=f(x*)-t*成立,故(x*,t*)为规划(Q)的一个最优解。
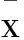
(7)
成立。因为(x*,t*)是规划(Q)的一个最优解,所以对任意的x∈X和t∈R有g(x*)-t*≥0和
(8)
此时不等式(7)可变为:
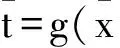
(9)
不等式(9)与(8)矛盾,所以,x*不是规划(P)的一个最优解。
综上所述,引理3得证。
由引理3和其证明过程可得以下命题:
命题2x*∈X是规划(P)的一个最优解当且仅当(x*,t*)为规划(Q)的一个最优解,其中t*=g(x*)。
4 一些特殊DC规划的最优性条件
先考虑一类DC规划:
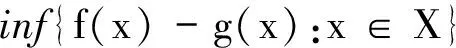
(10)
其中: f和g是Rn上的两个凸函数;X是Rn内的闭凸子集。
文献[12]给出了规划(10)的一个最优性条件,即引理4,并利用互反原理和集合的鲁棒性等知识对引理4进行了证明。本文将给出引理4的第2个证明方法。
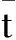
x∈X,t∈R}
证明
x∈X t∈R}
成立。
事实上,因为点x*∈X是问题(10)的一个最优解,对任意的x∈X有下列不等式成立:
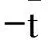
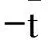


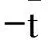

(11)
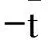
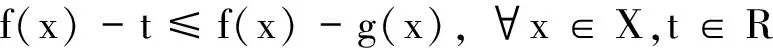
由x和t的任意性可知
(12)
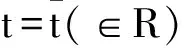
即点x*∈X是问题(10)的一个最优解。
综上所述,引理4得证。
下面考虑一类特殊DC规划:
(13)
其中:f是Rn上的凸函数;g是Rn上的连续可微凸函数,且ui 成立,且G(x)是Rn上的凸函数。因此,规划(14)为凸规划。 (14) 由DC规划(13)和凸规划(14)之间的联系,可得以下定理: (15) 综上所述,定理1得证。 本文利用最优化理论和算法的相关知识,使用不同于以前的方法对DC规划中已有的一些定理和结论进行了详细证明,并对其中一些结论进行了推广,阐述了一类DC规划和其对应的反凸规划的最优解之间的联系与区别。此外,本文还运用L-次微分等相关知识,提出并讨论了一类特殊DC规划和一类凸规划的最优解之间的关系。本文的内容和结果对研究DC规划具有重要的理论意义和应用价值,在此基础上,还可以进一步对DC规划的最优性条件和最优化算法进行研究和探索。 [1]ABSIL P A,TITS A L.Newton-KKT interior-point methods for indefinite quadratic programming[J].Computational optimization and applications,2007,36(1):5-41. [2]WU Z Y.Sufficient Global Optimality Conditions for Weakly Convex Minimization Problems[J].Journal of Global Optimization,2007,39:427-440. [3]TSENGA C L,ZHANB Y,ZHENGB Q P,et al.A MILP formulation for generalized geometric programming using piecewise-linear approximations[J].European Journal of Operational Research,2015,245(2):360-370. [4]SHEN P P,LI X A.Branch-reduction-bound algorithm for generalized geometric programming[J].Journal of Global Optimization,2013,56(3):1123-1142. [5]周波,钱堃,马旭东,等.一种新的基于保证定界椭球算法的非线性集员滤波器[J].自动化学报,2013,39(2):150-158. [6]ASTORINO A,MIGLIONICO G.Optimizing sensor cover energy via DC programming[J].Optimization Letters,2016,10(2):355-368. [7]DINH T P,HOAI A L T,PHAM V N, et al.DC programming approaches for discrete portfolio optimization under concave transaction costs[J].Optimization Letters,2016,10(2):261-282. [8]HOAI A L T,DINH T P.DC programming in communication systems:challenging problems and methods[J].Vietnam Journal of Computer Science,2014,1(1):15-28. [9]HOAI A L T,NGUYEN M C,DINH T P.A DC Programming Approach for Finding Communities in Networks Neural Computation,2014,26(12):2827-2854. [10]HORST R,PARDALOS P M,THOAI N V.Introduction to Global Optimization[M].Second Edition.Kluwer Academic Publishers,2000. [11]TUY H.Convex programs with an additional reverse convex constraint[J].Journal of Optimization Theory and Applications,1987,52(3):463-486. [12]郝斯特,帕达劳斯,托伊.全局优化引论[M].黄红选译.北京:清华大学出版社,2003. [13]HORST R,THOAI N V.DC Programming:Overview[J].Journal of Optimization Theory and Applications,1999,103(1):1-43. (责任编辑陈艳) Some Conclusions and Generalization of DC Programming FU Yu,MA Lin-Jing,LI Ke-ke (Chongqing Normal University, Chongqing 401331, China) For DC (difference of convex) programming, some theorems and conclusions of it were proved combined with the relevant knowledge of the optimization theory and method by using different methods. And on this basis, some of these conclusions have promoted. Furthermore, we expounded the relationship of the optimal solution between the type of DC programming and their corresponding reverse convex programming. Finally, the relation and difference between the optimal solutions of a special class of DC programming and its related convex programming were presented and discussed by using the knowledge of L-subdifferential and other related knowledge. optimization theory and algorithm; DC programming; reverse convex programming; optimum solution 2016-03-16 重庆市研究生创新训练项目(CYS16144) 付裕(1990—),女,四川巴中人,硕士,主要从事全局最优化研究,E-mai:619668521@qq.com。 format:FU Yu,MA Lin-Jing,LI Ke-ke.Some Conclusions and Generalization of DC Programming[J].Journal of Chongqing University of Technology(Natural Science),2016(10):163-168. 10.3969/j.issn.1674-8425(z).2016.10.026 O224 A 1674-8425(2016)10-0163-06 引用格式:付裕,马琳晶,李科科.DC规划的一些结论及推广[J].重庆理工大学学报(自然科学),2016(10):163-168.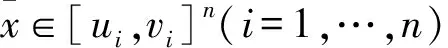
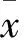
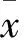





5 结束语

