基于灰色GM(1,1)联合预测模型的企业产值评估

朱　岚

(河海大学 商学院，南京 211100)



基于灰色GM(1,1)联合预测模型的企业产值评估

朱岚

(河海大学 商学院，南京 211100)

针对企业单位生产总值的预测问题，利用预测模型估计未来企业的发展规模以及经济能力。考虑到传统回归模型的不足，在灰色关联度和GM(1,1)模型的基础上提出了灰色G(1,1)联合预测模型。从灰色关联度出发寻找数据之间的关系，预测及加权生成模型关联系数，从而建立预测模型。最后根据2006—2012年企业生产的相关数据资料，利用该模型预测企业2013年的生产总值，预测结果说明该模型在预测方面是有效的。

灰色理论；灰色关联度；预测模型；GM(1,1)模型；生产总值；回归分析

当下中国推行财政分权制度，在这样的体制下地方政府在发展地方经济、引进投资、保障就业、提升地区 GDP增长等方面有着内在的动力[1-3]，这些经济指标在地方官员的考评机制中的地位也愈显重要。从1990年资本市场的建立，到现在20余年的发展历程充分说明公司企业已经成为国民经济发展的中坚力量，优秀的企业更是带动地方经济发展的重要力量[4-7]。优良的企业不仅拥有较高的经济资源利用效率，还能吸引更多外部的经济资源，在经过企业经营提高企业产值同时也对地方经济增长做出更多贡献，为企业所在地带来丰厚的“超额收益”。企业是提升地方经济水平最具活力的微观主体，是推动地方经济发展的源动力。企业的区域分布情况基本上反映了我国地方经济的发展状况，企业数量多、质量高的地区是经济较为发达的区域。具体地说，企业生产产值的增长带动地方GDP 持续增长，提高地方经济发展水平。对地方政府及企业而言，企业生产产值都是及其重要的衡量指标，从长远发展的角度来看地方政府部门以及企业本身对企业未来能够创造的产值更要密切关注，因此对于企业未来的产业产值的估计显得尤为重要。鉴于此，本文在现有文献的基础上研究合理估算企业未来产值的方法。

1　构建灰色联合预测模型

查阅以往的文献可知：对于多因素统计分析通常采用回归分析的方法[8]，即从事物之间的因果关系出发研究数据变化的规律，并且建立预测模型对后期未知数据进行预测。在预测模型比较重要的有马尔可夫模型、灰色预测模型等，其中灰色预测模型主要是利用原始数据累加生成序列建立模型进行数据预测，GM(1,1)模型是基础和核心[9-15]。为了克服基础模型预测精度不高以及模型仅从序列本身寻找数据变化规律的局限性，利用灰色关联度能通过刻画数据序列所对应曲线的相似程度的特性建立模型，实现精确度较高的数据预测[16]。我们将这种预测时间序列关系发展趋势且包含灰色关联度的GM(1,1)模型称为灰色联合预测模型。

1.1灰色关联度以及GM(1,1)模型

在传统的统计分析中，有一种利用位移差反应序列变量发展过程的邓氏关联度，但这种关联度在对序列间的关系量化的结果不唯一且不规范，量纲一化处理也不能发挥很好的作用[17-19]。在此给出一个关于灰色关联度较优的定义。

定义1设数列Xi=(xi(1),xi(2),…,xi(n)),i=0,1,2,…,m，称Δi(t)为序列Xi在t-1→t的数据增量，t=2,3,…,n，即

(1)

且有

(2)

这时，Ei为数值增量Δi(t)绝对值的平均值，∂i(t)为数值增量Δi(t)的均化值。

根据以上定义的变量值有：

(3)

(4)

其中，r0i(t)，r0i分别称为序列Xi与X0的灰色关联系数以及灰色关联度。

定义2设序列Xi=(xi(1),xi(2),…,xi(n)),i=0,1,2,…,m。当i=0时，称Xi为因变量序列；当i≠0时，称Xi为自变量序列。

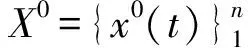
(5)

1.2模型关联系数的预测以及加权生成

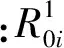
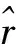
(6)

x0(k)与xi(k)的关联系数为

(7)

则r0i(k)成为由GM(1,1)模型的预测值以及序列Xi与X0的灰色关联度在λ下的生成值，可以看出r0i(k)受到序列之间的传统关联度以及发展趋势的双重影响，对于λ∈(0,1)，一般取λ=0.5。

1.3预测变量的预测公式推导

根据式(3)可知：

(8)

根据定义1的相关内容，对表达式进行推导可得：

1) 当X0是单调增长序列时，

2) 当X0是单调减小序列时，

由以上2个公式可以根据基期的数值计算下一时期的数值，完成预测工作。

1.4灰色联合预测模型的建立

在一般的应用回归分析中，因变量通常会受一个或多个自变量的影响，从而会表现出特定的性质，这些特征可以通过特定的函数关系来表现。作为影响因素的不同自变量对因变量产生不同程度的影响，可以用回归系数来表示影响程度，其回归系数越大表示影响作用越明显。同样地，对于建立的灰色联合预测模型，灰色关联系数体现了自变量序列对因变量序列的影响程度，测量自变量序列与因变量序列之间关联程度的灰色关联度也能表现出特定的函数关系，其中灰色关联系数越大表明自变量与因变量序列间的影响越大。那么，在这种意义上可以说回归系数与灰色关联系数有着相同的意义。

基于上面对于灰色关联度以及预测模型的理论分析，结合回归分析的方法以及回归模型的回归特性，现在就可以通过事物之间的因果关系建立灰色联合预测模型。

首先假设

那么灰色联合预测模型为：

(9)

2　预测模型的应用

通常用国内生产总值(GDP)的数值大小来衡量国家的经济规模，同样我们用企业结算期(一般情况下是以年为结算单位)内的生产总值(GDP)来表现一个企业的经济规模。根据相关经济专家的意见，选择该企业的生产总值(GDP)(X0，亿元)、企业固定资产投资(X1，亿元)以及企业贸易总额(X2，亿元)为变量的时间序列。为了更直观地表现本文提出的预测模型结果的精确性，用GM(1,1)模型、GM(1,3)模型、回归模型以及灰色联合模型同时进行预测，最后比较分析4种模型的预测结果。根据统计资料，整理出Y省的大型企业W在2006—2012年的上述3个量的具体数值，如表1所示。

表12006—2012年企业的GDP、固定资产投资以及贸易总额亿元

年份2006200720082009201020112012X08960096003102390116790136725183212208971X1327013700843199552117009188600109912X24699510061988541115381433117590

1) GM(1,1)模型

利用数据资料以及GM(1,1)模型的相关计算方法，计算得到a=-0.18,b=62 751.14，则模型预测公式为

计算得到：x0(8)=294 071.11。

2)GM(1,3)模型

同样地，可以得到 ：

代入数值计算得到：x0(8)=313 499.04

3) 回归模型

利用Eviews软件将表1中的数据进行处理，根据处理结果建立回归模型，即

x0=3.54x1-11.39x2+22 970.98

将统计资料中x1，x2的值代入上式可以得到第8年的生产总值x0(8)=261 500.11。

4) 灰色联合预测模型

根据本文的理论分析，首先可以根据式(1)计算序列的数值增量，结果见表2；其次根据式(2)计算序列数值增量的均化值，结果见表3；最后根据式(2)计算X0，X1，X2的灰色关联系数，结果见表4。

表2　2006—2012年企业的GDP、固定资产投资以及贸易总额的数值增量　亿元

表3　2006—2012年企业的GDP、固定资产投资以及贸易总额的数值增量均化值　亿元

表4　2006—2012年企业的GDP、固定资产投资以及贸易总额的灰色关联系数

从表4的数据可以得到关联系数的序列为：

R01=(0.97,0.86,0.85,0.89,0.57,0.78)

R02=(0.87,0.84,0.76,0.71,0.51,0.83)

从而计算得：r01=0.869 9，r01=0.738 9。

以下根据R01，R02建立GM(1,1)模型，利用式(6)以及式(7)计算得到关联系数的预测值以及加权预测值(λ=0.5)分别为：

r01(7)=0.737,r02(7)=0.671

现在就可以建立企业生产总值X0与企业固定资产投资X1、企业贸易总额X2的预测模型，根据式(9)可得：

(10)

通过查阅企业提供的资料可知：2013年该企业的固定资产投资以及贸易总额分别为138 016和217 993。将这些数据应用到式(10)中得到：

x0(7)=209 500,r01(7)=0.741

E0=20 001, ∂1(8)=2.125

计算得到固定资产投资X1的预测值为：

x01(8)=259 112.13

同理得企业贸易总额X2的预测值为：

x01(8)=239 312.11

利用资产投资与贸易总额的预测值以及公式(10)得到生产总值X0的预测值为：

x0(8)=0.538×259 112.13+0.462×

239 312.11=249 964.52

为了更加直观地看出4种模型预测结果的优劣，现将每个模型的预测结果与实际数值之间的误差计算出来如表5。

从表5中的数值看以明显地看出：灰色联合预测模型计算出的预测值与实际数值的误差百分数比其他3种模型的都要小，甚至与GM(1,3)模型的误差有几十倍的差距。从理论来看：回归模型预测精准度低主要是因为只取了企业近7年的相关数据，样本容量相对来说较小；GM(1,1)模型仅仅依据数据序列本身的规律去进行预测，而没有考虑到其他因素的影响；GM(1,3)模型的理论体系相对来说还不完善，没能处理好误差的累积影响，进而导致预测结果误差比较大；灰色联合预测模型是在以上模型的基础上，集合各个模型的长处，改进以往模型的不足，以及巧妙利用灰色理论的优点，因此才能得到比较精确的预测结果。

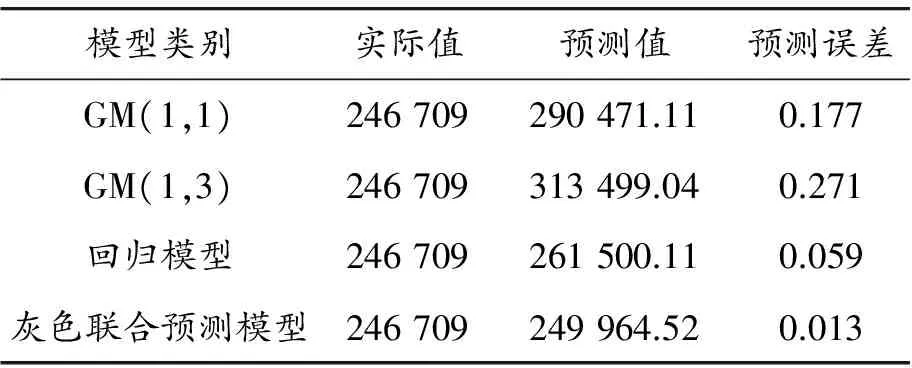
表5　2013年企业的生产总值(GDP)的预测值及误差比较

3　结束语

本文依据常规统计分析中经常用的回归分析理论，考虑到样本容量等相关影响因素对于因变量的影响，结合灰色理论的优点提出了一种新的预测模型。灰色联合预测模型从灰色关联度的角度分析事物发展变化的影响因素及其影响程度，通过GM(1,1)模型预测影响因素的变化趋势，然后按照回归分析的建模思想构建预测模型。经过实例的验证，该预测模型的预测结果比常规预测模型的结果更准确。需要注意的是，应用该模型进行预测计算时要求选择的数据样本量较小以及序列满足单调性，这样能确保模型预测的结果精确程度是一个理想的结果。

[1]段杰,张娟.基于灰色预测的深圳文化创意产业发展对经济增长贡献研究[J].中国人口资源与环境,2014(3):457-460.

[2]刘笑冰,陈建成,何忠伟.基于MGM(1,N)模型的北京创意农业发展灰色预测[J].中国人口资源与环境,2013(4):62-67.

[3]杨华龙,刘金霞,郑斌.灰色预测GM(1,1)的改进与应用[J].数学的实践与认识,2011(23):39-47.

[4]张子余,张天西.“真实销售行为”的动态选择与经济后果[J].南开管理评论， 2011(6):128-136．

[5]唐雪松,周晓苏,马如静.政府干预、GDP 增长与地方国企过度投资[J].金融研究，2010(8):33-48.

[6]李梦,李勇.市场化水平、所有制结构与经济周期[J].中国经济问题,2013(6):28-40.

[7]顾鸣润,杨继伟,余怒涛.产权性质、公司治理与真实盈余管理[J].中国会计评论,2012(3):255-274.

[8]TAYLOR G.K,XU R Z.Consequences of Real Earnings Management on Subsequent Operating Performance[J].Research in Accounting Regulation,2010(2):128-132.

[9]董奋义.基于新改进GM(1,1)模型的中国企业债券融资发展预测[J].中国管理科学,2007,15(4):93-97.

[10]张岐山.提高灰色GM(1,1)模型精度的微粒群方法[J].中国管理科学,2007,15(5):126-128.

[11]何昕,陈亚青.应用改进的灰色模型预测民航管制员数量[J].实验科学与技术,2010(2):28-30.

[12]祝华远，崔亚君，高峰娟.灰色预测模型在军机飞控系统故障预测中的应用[J].四川兵工学报，2014(6):44-46.

[13]王娜，涂建军，孙祥龙,等.基于灰色模糊评价法的耕地社会功能评价--以重庆市为例[J].西南大学学报(自然科学版)，2014(10):144-149.

[14]郑瑶，席泽敏，许杰.基于灰色关联分析的备件保障能力评估方法[J].四川兵工学报，2014，35(3):62-64.

[15]宋严.灰色关联分析与支持向量机相融合的网络安全态势评价[J].激光杂志，2015，36(4):147-150.

[16]任工昌,刘丽,苗新强.改进灰色模型在电力负荷中的预测分析及实现[J].工程设计与制造,2010(2):232-234.

[17]闫永权.基于频繁的Markov链预测模型[J].计算机应用研究,2007，24(3):41-46.

[18]李志强.山东省国民生产总值预测的灰色模型[J].山东农业大学学报(自然科学版),2008(2):263-266．

[19]GUNNY K A.The Relation Between Earnings Management Using Real Activities Manipulation and Future Per-formance:Evidence from Meeting Earnings Benchmarks[J].Contemporary Accounting Research,2010(3):855-888.

(责任编辑杨黎丽)

Assess of Enterprise Value Based on Grey GM(1,1)Forecasting Combined Model

ZHU Lan

(School of Business, Hohai University, Nanjing 211100, China)

This paper used the predictive model to estimate the scale of future development and economic capability about the prediction of gross production enterprises. Considering the shortcomings of traditional regression model, grey G(1,1) forecasting combined model gray correlation was raised on the basis of grey correlation degree and GM (1,1) model. We found the relationship between the data by gray correlation, and forecasted and weighted correlation coefficient in order to establish predictive models. Finally, according to the production data in 2006—2012, we used the predictive model to predict the corporate GDP in 2013, and the results showed the effectiveness of the model prediction.Key words: gray theory; gray relational grade; prediction model; GM (1,1) model; GDP; regression analysis

2016-04-04

国家社会科学基金资助项目(13zxb082)

朱岚(1990—)，女，江苏泰州人，硕士研究生，主要从事企业管理、人力资源管理研究，E-mail:zhulan0928@163.com。

format：ZHU Lan.Assess of Enterprise Value Based on Grey GM(1,1) Forecasting Combined Model[J].Journal of Chongqing University of Technology(Natural Science)，2016(10):175-180.

10.3969/j.issn.1674-8425(z).2016.10.028

O29；F275

A

1674-8425(2016)10-0175-06

引用格式：朱岚.基于灰色GM(1,1)联合预测模型的企业产值评估[J].重庆理工大学学报(自然科学)，2016(10):175-180.