基于双基链的快速标量乘算法研究

武永波，彭青松，高茂庭

（上海海事大学信息工程学院，上海　201306）

基于双基链的快速标量乘算法研究

武永波，彭青松，高茂庭

（上海海事大学信息工程学院，上海201306）

在有限域GF（2m）上，实现椭圆曲线密码体制（ECC）中关键运算是标量乘算法，该算法也是椭圆曲线密码体制中耗时最长、极易受到攻击的运算之一。为了提高椭圆曲线密码算法计算的安全性和效率性，从分析以2、3为底的双基链椭圆曲线标量乘特点出发，在现在有的双基链算法基础之上，提出一种新的快速标量乘算法。新算法中，通过应用米勒算法和2-3链相结合的方法，寻找出权重更小的双基链。此外，考虑到小权重也有其局限性。引入了技术Tate配对与2-3链相结合来提高算法效率，比基于贪心算法的双基链更加高效。经仿真实验比较分析和研究，表明该改进算法可以很好提高计算效率，并且同时能大大降低存储量。

椭圆曲线密码体制；标量乘法；双基数系统；Tate配对

0　引言

1985年，N.Koblitz和V.Miller各自独立地提出了椭圆曲线公钥密码体制 （ECC，Elliptic-Curve-Cryptographic），这是椭圆曲线理论在密码学中又一次全新的应用［1］。椭圆曲线密码体制的安全性是基于椭圆曲线上离散对数问题求解的困难性，并且目前还没有找到解决此问题的亚指数时间算法，具有一些其他公钥密码体制无法比拟的优点，例如在相同的安全强度下，具有系统参数和密钥尺寸短 （如160 bits的ECC和1024 bits的RSA具有相当的安全强度），选择机会较大等特点［2］。正因如此，十几年来，ECC一直是数学界、密码学界和计算机科学界所关注的重大课题。ECC加解密方面速度快、节省能源、节省带宽和节省存储空间，特别适用于ECC密码引擎协处理器的SIM卡、Smart卡和FPGA、ASIC芯片等的开发。凭借其诸如此类众多的优点，ECC技术在信息安全领域中发挥越来越大的作用［3］。

在ECC中，标量乘的计算决定着椭圆曲线密码体制的运算效率。所谓的标量乘即在域Fq上的椭圆曲线E上的一个点P和已知的一个整数n（即标量），计算nP的过程就是计算标量乘的过程，可以分为3级模块来完成：顶级模块为点乘运算；中级运算模块是把点乘运算分解成了有限域Fq上点加 （ECADD）和倍点（ECDBL）构成的Abel群上的运算；最底级的运算模块就是完成有限域模块上的所有运算，包括Fq上大整数的域乘法、域逆和域平方运算［4-5］。

椭圆曲线密码由于具有密钥短、安全性高等其他公钥密码体制所无法比拟的特点，近年来已经成为密码学领域研究的热点之一［1-2］。计算标量乘nP（又称点乘法）是最基本、最耗时的操作，在许多基于椭圆曲线的密码方案中，科学家已经提出多种形式多种方法来改进标量乘算法的运算效率：

（1）通过对标量n展开形式的优化，来提高运算效率，代表性算法有NAF表示、τ-adic表示、双基表示等［3-6］。

（2）引入预计算的窗口算法和comb算法等［3］。

（3）根据椭圆曲线的特点使用不同的坐标表示，例如仿射坐标、射影坐标和Inverted Edwards坐标［7］等。

因此，从抗多种功耗攻击的能力和系统计算性能优化两个方面考虑，本文结合基于贪心算法的双基数系统标量乘算法，给出了一种执行效率高和安全性强的防御方案。主要从标量n入手，通过tate配对来优化系数n的表示，使得标量n在基于tate配对的双基链基础之上展开，并且这样双基链展开速度更加高效，从而达到加快标量乘算法的目的。

1　基础知识

1.1椭圆曲线标量乘

设Fq是一个有限域，P是定义在有限域Fq上的椭圆曲线E（n）上的一点，n是一个大整数。根据椭圆曲线上点的加法公式将点P与自身相加n次，即椭圆曲线上的点乘nP的计算公式为：

若n＜0，Q=［-n］（-P）=-（-n）P，n称为标量，nP称为椭圆曲线标量乘法。一般的，将P+P+…+P记为nP，即nP=P+P+…+P。特别的，OP=O（O是无穷远点）。标量乘运算是椭圆曲线密码体制中的核心运算，加密和验证时都需要计算标量乘，它的运算速度决定着椭圆曲线密码体制的运算速度。因此，高效率标量乘运算的实现是设计椭圆曲线密码系统过程的关键之一［6-7］。

当然，影响标量乘法运算效率的因素很多，例如特殊的曲线的特性会有助于提高运算效率，如在ECDSA签名生成中，若点基点P是固定的，点乘算法可以利用一些与计算数据提高运算效率，而这些数据仅与P有关，与n无关。

1.2基于贪心算法的双基数系统

双基数字系统（DBNS，Double Base Number System）是其中每一个正整数n表示为形式的数字的总和或差的表示方案pbqt，即：

式（2）中的m是DBNS的汉明重量。

在本文中，主要考虑p=2，q=3，通过贪心算法可以很简单地找到一个表示整数n的方法。即，每次都寻找a和b的值，使得2a3b最接近指定的整数。

然后计算其差异，继续循环这个过程，直到0的时候停止算法。

贪心算法常用来求解整数的双基表达式，在文献［8］中提出了基于LineSearch方法的贪心算法，该算法在效率方面有着良好的表现。但是，贪心算法并不能保证多轮迭代后的结果仍然是最优的。在O（log n/loglogn）时间复杂度内利用贪心算法来求出其DBNS的形式［9］。

例：令n=841232，利用贪心算法可以求出n的DBNS表示：

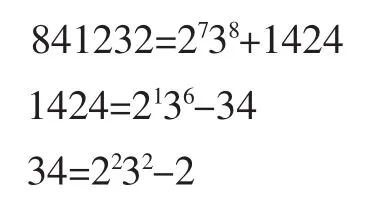
综上所述，841232=2738+2136-2232+2对于整个计算而言，最简单直接的方法计算双基链。因为它的形式下，一个双基链使得可能仅使用增加一倍和两倍的先前的部分结果，并与加法和减法累积达到nP。其中一个最有意义的就是如何就椭圆曲线的效率选择最合适的双基链，然而，这并不是那么简单的事情。通常情况下，这样计算出来的双基链并不适合椭圆曲线标量乘，因为通常不考虑数的双倍和三倍的最优化。例如，219+ 312是最短DBNS表示1055729。但是更佳组合运算在NAF中表示是220+213-210-24+1。为了获得更合适的双基链，需要提出改进的算法。

1.3基于Tate配对的双基链

设E（Fq）是组上的椭圆曲线有限域Fq，并且n和正整数q互质（一般情况下n为素数）。用E（Fq）［n］表示在Fq中的n拐点。令P∈E（Fq）［n］和Q∈E（F（qk））［n］，用DP和DQ表示E的两个除数，其中分别满足DP=（P）-（∞）和DQ=（Q）-（∞）。让fp是椭圆曲线的除子是div（fp）=n（P）-n（∞）的有理函数［4］。减少的Tate对τn为τn：E（Fq）［n］×E（Fqk）［n］→F*qk

定义为：

如果k>1且Q不具备Fq的有理性，可以避免与除数并简单的与点Q并行，这样就可以减小Tate就如上公式。

米勒算法可以很有效地计算Tate配对，它解决的主要问题是如何构造一个有理函数Fq，使得div（fp）=n（P）-n（∞）。米勒的思想是将加倍和加算法结合起来，标量乘［n］P上直线穿过在加法/加倍方法中使用的点的过程。

设［j］P和［k］P为椭圆曲线E上两个不同的点（均为P的倍数），其中j，k∈Z，经过这两点的直线l的除子为：div（fζp）=n（P）-n（∞）

div（ζjp，kp）=（［j］P）+（［k］P）+（-［j+k］P）-3（∞）进一步来说，穿过［j］P和-［j］P的竖线表示为ζjp，那么div（ζjp）=（［j］P）+（-［j］P）-2（∞）。

2　双基链标量乘算法的改进

双基数系统可以将标量n的双基数链表示的长度限制在o（logn/loglogn）范围内，这样就可以减少标量乘法中的上层计算。在底层域快速算法方面，可以直接计算3kP快速算法。通常情况下，计算Tate配对的一个重要部分是在DQ对每一个点S求值，米勒算法的主要思想是：任取点R，DP=（P+R）-（R），∀j∈Z，定义DjP=j（P+R）-j（R）-（jP）+（o）则存在有理函数fj使得div（fj）=DjP，特别地，fn=fP成立，因为P∈E［n］，使nP=0。

为了简化操作，两个条件写为：

（1）f1=1

米勒的算法对于nP用加法链计算FP，也就是说，（FP）=N（P）N（∞）。这个算法是通过将n用二进制位展开表示的，那么，可以将标量n用双基链表示，其中在米勒算法的基础上利用双基链表示标量n来计算标量乘。

算法1基于米勒算法的双基链

Input：bi，ti，n=，si=｛-1，1｝，b1≥b2≥…≥bm≥0，t1≥t2≥…tm≥0，P∈E（Fq）［n］，Q∈E（Fqk）［n］

Output：f=fn（Q）

1：if s1=1 then

2： f←1，Z←P

3：else

5：for i←1，2，…，m-1 do

6：u←bi-bi+1，v ti-ti+1

7：for j←1，2，…，v do

9：for j←1，2，…，u do

10：f←f2·，Z←2Z.

11：if si+1=1 then

13：else

15：return f

算法1中，尽管双倍乘法和三倍乘法取代了之前的加法减法，在实际场合中可以不用完全取代。因为至少存在一个u或v一定大于0，每次加法和减法都被组合为fj2或者fj3。并且在算法1的步骤9中，K.Eisentrager［11］曾这样提及过，可以用PZ，-3Z来表示一个抛物线穿过三次方程。评估函数成本中，使用抛物线方程则将会降低运算成本。

用α2，α3分别表示米勒算法中2倍和3倍的花销，点加和倍点相结合的总成本被写成α2+β2+。相似的，2倍和减法记为α2+β2-，3倍和加法相结合记为α3+β3+。

如果2Pi±Pi和3Pi±P作为组合操作被执行，那么希望β2+≠β3+和β2-≠β3-成立，然而，如果分开执行的操作（作为原始形式米勒算法），那么，将会导致β2+=β3+和β2-=β3-成立。当然相同的符号可以用于“标准”（非配对）标量乘法运算，其中α2，α3，β2+，β2-，β3+和β3-应解释为相关联的组的运行成本（无功能评估）。

3　基于Tate配对双基链算法

3.1最短双基链算法

如上所述可以将多个步骤组合操作并且执行，这样能降低算法运行成本。从而可以定义双基链C（i，j），其中i，j分别表示链表中2的指数和3的指数的最大值。也就是说其他项任意项±2a3b都满足a＜i，b＜j。

注意到ni，j和ni，j=0的情况，如果链表Ci，j存在最大项，则为正数。如果链表存在最大项，则为负数。

对于ni，j，如果li，j是最小的链表。其中包含子链表。Ca，b对于na，b来说，并且a≤i，b≤j那么Ca，b一定比na，b小。相似的加个负号也是一样的。

对于我们在数值实验中，我们使用的评估算法成本［6］，因为它们覆盖的整个范围内，我们感兴趣的是它们当然应该由具体的比例换成是否需要一个具体链。

由于双基链为基础，如果系数 α3/α2≈log23= 1.58496...（对应于基2和基3的相对长度扩展）。即使α3/α2与log23相差比较多，我们的算法仍然可以使用，但输出很可能接近单基表示在更有利的形式。

那么，令Ci，j是任意ni，j的双基链表。只要Ci，j！=0则有以下情况。

1、Ci，j=Ci-1，j（当且仅当ni，j=ni-1，j）

2、Ci，j=2i-13j+Ci-1，j（当且仅当ni，j=2i-13j+ni-1，j）

3、Ci，j=2i-13j+（当且仅当ni，j=2i-13j+）

4、Ci，j=Ci，j-1（当且仅当ni，j=n（i，j-1））

5、Ci，j=2i3j-1+Ci，j-1（当且仅当ni，j=2i3j-1+ni，j-1）

6、Ci，j=2i3j-1+Ci，j-1（当且仅当ni，j=2i3j-1+）

上面给出了Ci，j，由i，j其中任何一个减少或者增大，都可以看出链表相邻两项的关系。其中也包括同时增大同时减小。其关系如表1所示。

表1　Ci，j和 ni，j关系

表2　Ci，j中最大的项是2ij-13jor 2ij3j-1

定义 ij，就获得2ij3j-1＜2ij-13j≤nij，j=n

所以 nij-1，j≠nij，j而且 nij，j-1≠nij，j，那么 Ci，j一定会进入情况2，3，5，6。通过定义，其中链表中最大项，是2ij3j。

根据以上结果，得到的算法2。i和j都是从0开始，分别是从2和3的幂。

算法2最短双基链算法

Input：n>0

Output：

1：Cj←Ø，←Ø for each j

2：for i←0 to「log2（n+1）⌉do

4：if im＜i then

5：m←m-1

6：for j←0 to m do

7：find Ci，jandfrom sheet 1，cause Cj=li-1，j

8：find Ci，jandfrom sheet 2，cause Cj-1=li，j-1

9：Cj←Ci，j（Cj=li，j）

11：if i=ijthen

13： lj←min（Cj，）

14：return l

很显然，给定任意链Ci，j，以上所有条件均为互斥的。如果Ci，j链存在，那么，链中最大的项是r，r=2i-13j那么第二项如果是正，那么转到情况2，如果第二项是负，那么转到情况3。

如果链表中最大的项目r=2i-13j-1。那么第五项如果是正，那么转到情况5，如果第六项是负，那么转到情况6；如果r=2a3j的形式其中a≤i-2那么就只能是情况1；如果r=2i3b的形式其中b≤j-2那么就只能是情况4。

只有当ni，j=ni-1，j-1的时候，那么情况1和情况4同时发生。如果r=2a3b的形式其中a≤i-2，b≤j-2那么链表就会同时进入情况1和情况4。

虽然上面这个定理在寻找最佳双基链的算法中有些时候不是必须的。对于每一个j而言，都存在一个最小的链（如果没有j，那么可以完全忽略）。

3.2基于Tate配对双基链算法

在3.1所述链，我们仅仅对它们的汉明权进行了优化。然而，在实践中，这通常不是获得最快配对计算的最佳方法。根据基础组合运算，一些操作可被组合（例如加倍加入变成“加倍并加上”），并且2i3j可以将其改变（因为点加法和点减法在米勒的算法不同的效果）。

在本节中，我们考虑了成本与每一个类型的组合运算，从n的双基链表示米勒算法方面。由于我们的算法计算从最低一项的标量上升，但米勒的算法从最显著长期下降，我们必须调整我们评估相应的成本的方式。

此外，我们选择相结合的操作方式可能取决于有多少增加一倍和两倍的连续两项链之间进行。然后，我们需要分开链成子情况：

根据链的最大项的形式，可以将Ci，j分成三种情况：

最大项是形式2i3b而且b＜j，则

最大项是形式2a3j而且a＜i，则

最大项是形式2a3b而且a＜i和b＜j，则

对于Ci，j和Ci，j两种情况对于任何i，算法都仅仅保留一个副本。而该算法i=ij=「log2（（n+1）/3j⌉其中j的变化是有固定的i来决定的。因此，「log3（（n+1）/2j⌉∈｛「log3（（n+1）/3j⌉，「log2（（n+1）/3j⌉+1｝因此im=i-1等式可能成立，所以我们不需要考虑配对（im，m）。

正如上一节所讲，我们认为，对于任何i和j都存在C-1，j=Ø=Ci，-1，这样不处理负数的情况，也是与实际相联系的，算法会更加高效。在实际执行它会更有效分开处理这些情况，从来没有使用负指数。特别是，从定义可以得到ι0，0=0=

设n是一个正整数，则算法2返回最小双基链O（（log n）2）步骤O（（log n）4）位操作），以及需要O（（log n）3）内存位。

如果在链中的只计算2和3的权重 （例如，288被记录为一配对（5，2）），则每个链减小的内存需求到O（log n log log n）。如果它们被记录为它们的区别（再次以2的幂和3的幂）与前一项，每个链的内存要求为O（log n），所以算法2的内存要求可以降低到O（log n）2）位。

算法3预计算最小最优双基链算法

Input：n>0，计算α2，α3，β2-，β2+，β3-，β3+

Output：

2：for i←0 to「log2（n+1）⌉do

4：if im＜i then

5：m←m-1

6：for j←0 to m do

13：if i=ijthen

15：lj←min（Cj，）

16：return l

如果我们假设加速整数计算，每算法的步骤的成本降低到O（log n）时间位操作，并且该算法的总成本变得O～（（log n）3）位的操作。

此外，我们提出“正链”和“负链”，其中所有的术语具有相同的符号（除非在负链的项）的概念。

正链只能从ιi，j（而不允许任何），一直递增到ιi，j。同样，负链从（允许ιi，j）一直递增至个（最后期限为正），适应算法来做到这一点很简单。在提出的操作成本［6］，负链要比正链更有利（因为二者β2-和β3-是大约三小于β2+和β3+次），实验结果表明，其成本仅仅比最小链稍大。

4　算法实验比较和分析

本节将新提出的算法与第一节中提到的算法进行了性能的分析和效率的比较。对每个区间都随机选取大量的素数进行数值实验。其中实验中需要对比的5种算法分别是基于双基链的贪心算法、Dolce和Habsieger（+符号）无限制平均汉明权重算法、最小Tate双基链算法、最小负链算法和NAF理论值。实验中主要分别对5种算法的汉明重量和消耗的总成本进行比较，得出以下结论。

对每比特的汉明重量和每比特消耗的成本进行对比。结果示于图1和2。对于成本的评估，使用系数之间的比例［6］为：α2=1，α3=1.5705，β2-=0.1107，β3+=0.3648，和β3-=0.1047。

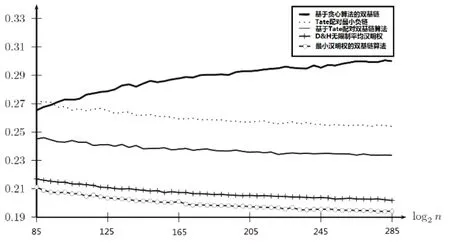
图1各算法每比特的汉明重量

图1中，由于n比较大，横坐标用log0n代替。粗线表示双基链贪心算法，+符号表示Dolce和Habsieger无限制平均汉明权重，o符号表示最小的汉明权，普通线为最小化Tate对成本，虚线表示最小负链，以及用于NAF理论值。

每个“标准”的二进制表示的位的平均汉明权重为0.50，而对于NAF它减少到0.33。从图1中，贪心算法的性能似乎减少为n的增加到慢慢变更接近一个NAF，无限接近于0.30。另外，Doche和Habsieger和我们的算法（被认为所有三种情况下）的基于树的方法的性能稍微增大为n个的尺寸增大，但远不可能接近所预期的用于DBNS的算法。

从图1中，似乎更合理考虑双基链如具有线性增长，汉明重量约为0.25/bit的最小化的负链，0.23为双基链具有为双基最小化成本和0.19链以最小的汉明权重。基于树的方法，我们观察的下限为每约0.20bit的汉明权重，而Dolce［10］和Habsieger算法大概为0.215（1/4.6419）。

在配对计算性能方面，双基链以最小的成本配对提供了一个近似的12.3%的涨幅比原来的 （标准二进制）米勒算法（1.152α2/bit），4.22%，较NAF-配对（1.069α2/bit），较贪心的双基链低3.48%，比最低1.40%。

图2　各算法每比特的平均配对成本

粗线表示双基链贪心算法，+符号表示Dolce和Habsieger的无限制版本，o符号表示最小的汉明权，普通线表示最小化Tate对成本，虚线表示最小化的负链），以及用于NAF理论值。

结合在 Dolce和 Habsieger（在实践中大概为1.74%［10］）超过双基链具有最小汉明权和1.06%。使用负链和真正最小双基链之间的差异似乎是小于0.065%，由于减少了开销，这可以通过从具有较简单的程序的增益进行补偿。需要注意的是在大约每比特1.025α2，优化的链可以被认为是绝对的下限米勒状算法，其成本仅仅只有2.59%。

5　结语

我们提出的这个算法，能够更加有效的将整数n进行双基链表示。我们描述了如何适应我们的算法以最小化表示的任一汉明权或优化的链上的tate配对计算的效果。这些算法也可以很容易地适用于其他情况下（尤其是如果各个Tate对操作的成本改变）。我们还介绍了负链，其提供接近最佳的性能，并允许以简化的配对执行的概念。

适应多基地数字系统保留为一个开放的问题。三基链（例如2-3-5链）是一个自然延伸和最有可能需要我们算法的立体版本。人们也可以考虑双基链具有较大的系数集合［5］。适应我们的算法，以这些表示将需要更新的表结构，以及最有可能的一组较大的可能链的每个位置（i，j）。此外，我们还必须考虑到较大的位数在米勒算法的费用设置的影响。

［1］Bernstein D J，Lange T.Fast Addition and Doubling on Elliptic Curves［A］.Asiacrypt 2007［C］.Lncs 4833，2007.29-50.

［2］Chevallier-Mames B，Ciet M，Joye M.Low-Cost Solutions for Preventing Simple Side Channel Analysis：Side-Channel Atomicity［J］. Ieee Transactions On Computers，2004，53（6）：760-768.

［3］Cryptanalysis of A Remote User Authentication Scheme for Mobile Client-Server Environment with Provable Security Based on ECC. Information Fusion，2013，41（4）：498-503.

［4］Mishra P K，Dimitrov V.Efficient Quintuple Formulas for Elliptic Curves and Efficient Scalar Multiplication Using Multibase Number Representation［C］.Proc.Of The 10th International Conference on Information Security.［S.L.］：Springer-Verlag，2007：390-406.

［5］王圆圆，殷新春.基于双基数子集表示的快速标量乘算法［期刊论文］-江苏大学学报（自然科学版），2009（3）.

［6］On the Security of an Improved Password Authentication Scheme Based on Ecc.Proceedings of the Third International Conference Information Computing and Applications（Icica 2012），Chende，China，Lncs 7473：181-188.

［7］Pang Shi-Chun，Tong Shou-Yu，Congfu-Zong，et a1.An Efficient Elliptic Curve Scalar Multiplication Algorithm Against Side Channel Attacks［C］.Proceedings of the 2010 International Conference on Computer，Mechatronics，Control and Electronic Engineering（Cmce2010），Springer-Verlag，Berlin：2010：361-364.

［8］Hedabou，M.，Pinel，P.，B'En'Eteau，L.：Countermeasures for Preventing Comb Method Against Sca Attacks.In：Deng，R.H.，Bao，F.，Pang，H.，Zhou，J.（Eds.）Ispec 2005.Lncs，Springer，Heidelberg 2005，3439：85-96.

［9］李忠，彭代渊.椭圆曲线标量乘法中标量的有效表示［期刊论文］-南京师大学报（自然科学版），2010，33（3）.

［10］许凯平，郑洪源，刘锦峰等.椭圆曲线密码体制中快速标量乘方法研究［J］.计算机工程与应用，2011，47（15）：112-115．

［11］Lu C Y，Jen S M，Laih C S．A General Framework of Side-Channel Atomicity for Elliptic Curve Scalar Multiplication［J］.Ieee Transactions on Computers，2013，62（3）：428-438．

［12］Abdulrahman E，Reyhani-Masoleh A.New Regular Radix-8 Scheme for Elliptic Curve Scalar Multiplication Without Precomputation［J］.Computers，Ieee Transactions On，2015，64（2）：438-451.

［13］白羽，范恒英．一种改进的椭圆曲线标量乘的快速算法［J］．西南科技大学学报，2011，26（3）：48-52.

［14］Mishra P K，Dimitrov V．Eficient Quintuple Formulas for Elliptic Curves and Effieient Scalar Multiplication Using Muhibase Number Representation［C］.Isc 2007：Proceedings of the 10th International Conference of Information Security，Lncs 4779.Springer-Verlag，2007：390-406．

［15］Adikari J，Dimitrov V S，Imbert L_Hybrid Binary-Ternary Number System for Elliptic CurveCryptosystems［J］.IEEE Transactions Computers，2011，60（2）：254-265．

［16］周梦，周海波.椭圆曲线快速点乘算法优化［J］．计算机应用研究，2012，29（8）：3056-3058.

［17］Purohit G，Rawat A S，Kumar M．Elliptic Chive Point Multiplication Using Mbnr and Point Halving［J］．International Journal of Advanced Networking And Applications，2012，3（5）：1329-1337．

［18］Mahdavi R，Saiadian A Efficient Scalar Multiplications for Elliptic Curve Cryptosystems Using Mixed Coordinates Strategy and Direct

Computations［C］.Cryptology And Network Security（Lncs6467）．2010：184-198.

Elliptic Curve；Scalar Multiplication；Double Base Number System；Tate Pairing

Research on Fast Scalar Multiplication Algorithm Based on Double-Base Chain

WU Yong-bo，PENG Qing-song，GAO Mao-ting
（School of Information Engineering，Shanghai University of Maritime，Shanghai 201306）

In order to improve the security of elliptic curve cryptographic algorithms and efficiency of the existing side-channel attacks and scalar multiplication algorithm on the basis of a new scalar multiplication algorithm is proposed.Scalar multiplication is the elliptic curve cryptosystem（ECC）of the basic operation，is also one of the most time-consuming and vulnerable to attack.Elliptic curve scalar multiplication，2-3 double-base chain represents an integer N，can improve the efficiency of the scalar multiplication.In a scalar Multiplication algorithm，to find the optimal 2-3 double-base chain will takes longer than scalar multiplication itself，the cost of pay more.New algorithm，the application of Tate pairing and 2-3 chain combination，to find out better 2-3 chain.In addition，than 2-3 chain based on greedy algorithm.Simulation results show that the improved algorithm can reduce the storage with improving the calculation efficiency.

1007-1423（2016）29-0003-08

10.3969/j.issn.1007-1423.2016.29.001

武永波（1992-），男，河南开封人，学生，专业方向为软件开发方法与软件项目管理彭青松，男，工学博士，管理学博士生，副教授，硕士生导师，研究方向为安全管理、智能信息处理高茂庭，男，教授，研究方向为数据挖掘、数据库与信息系统

2016-05-27

2016-09-20