稀疏PCA网络：一种核自适应的卷积神经网络

杨凌，司宁博

（兰州大学信息科学与工程学院，兰州　730000）

稀疏PCA网络：一种核自适应的卷积神经网络

杨凌，司宁博

（兰州大学信息科学与工程学院，兰州730000）

卷积神经网络因其具有的能够处理高维数据和易于并行化的特点，近年来在图像处理相关问题中受到广泛应用。相比于目前所流行的使用大量图片集构建深层网络的设计方法，稀疏PCA网络更注重卷积核的构建。传统的卷积核构建方法需要大量计算时间或复杂的图像特征提取知识，稀疏PCA网络使用简单的PCA基向量来构建卷积核，并加入聚类步骤，从而引入自适应性与稀疏性。在结果上，稀疏PCA网络相比传统的PCANet在图像分类实验正确率上有所提高，相较于其他深度学习模型也获得了较好的结果。

卷积神经网络；PCA；稀疏表达；自适应；图像分类

0　引言

神经网络是一种模仿动物神经系统的模型，在机器学习问题中应用广泛。近年来，由于人们所处理的问题越来越大规模化，如何有效地从数据中提取特征成了机器学习中的重要问题。神经网络具有灵活的结构，可监督式地进行分类学习，也可无监督地提取特征。受到动物视觉皮层的部分激活这一特性的启发，卷积神经网络在其基础上采用了部分连通的结构，这使得它的模型参数大大减少，并且能够更好地学习到数据的局部特征［1］，被大量应用于图像与语音等问题中。卷积神经网络采用局部卷积核来提取特征，可以通过反向迭代算法训练出卷积核，从而替代传统的人工设计特征方法。

主成分分析法（PCA）是一种用于特征提取和数据降维的无监督学习方法，它能够找到数据的最大变化方向。从特征的角度来看，这些主要的变化方向即是数据的特征。因此，PCA基向量可以作为卷积核应用于卷积神经网络中。事实上，马毅等人提出的PCANet［2］就是用PCA基向量作为卷积核构建的三层网络，取得了和其他深层网络模型相近甚至更好的效果。为了更好地适应图像的局部特征，在PCANet的基础上，本文使用聚类算法构建出了一个过完备的PCA基向量词典，在特征提取时，自适应地在词典中找到对应的卷积核，使得每个图像片变为一个稀疏表达。

本文首先介绍了卷积神经网络模型以及传统的PCANet，之后介绍加入了聚类步骤的稀疏PCA网络，最后用稀疏PCA网络在CIFAR 10数据集子集上与其他深度学习模型进行了实验对比。

1　卷积神经网络

卷积神经网络从结构上可分为两个部分：卷积层和池化层。卷积层和池化层可叠加，从而构建出深层网络。图1是一种简单的卷积神经网络，由Y.LeCun等人提出［1］。

1.1卷积层

卷积层是将输入图片与多个卷积核进行卷积运算，从而得到多张特征图。每一个卷积核作为一个特征提取器，在整张输入图片上滑动，计算卷积，寻找出可能的边缘，纹理或者边角特征。使用多个卷积核，可以对输入图片的某一位置提取不同的特征。特征图表示了输入图片在对应位置上对于某种特征的激活程度，如果对应位置处的小区域图像片符合卷积核所代表的特征，则会得到较大输出。对于一张尺度为N×N的输入图片X和一个尺度为m×m的卷积核W，经过卷积运算的特征图Y的尺度为（N-m+1）×（N-m+1），特征图Y上每个点可表示为：

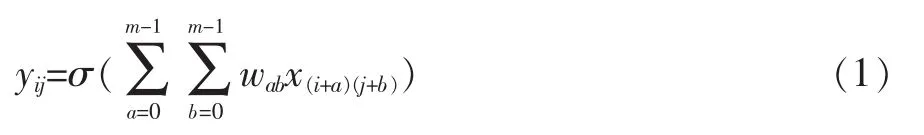
其中yij为特征图Y在（i，j）位置处的输出，xij为输入图片在（i，j）位置处的灰度值。wab为卷积核W在（a，b）位置处的值。σ（）是激活函数。通常，卷积层会将卷积结果输入一个非线性函数，将结果作为最终特征图中的值。常用的激活函数有sigmoid函数和近年来广泛使用的ReLU函数［3］。对于sigmoid函数，卷积层最终输出为：

对于ReLU函数，卷积层最终输出为：

1.2池化层

池化层又称下采样层，是对卷积层输出的特征图进行局部下采样。一般常用最大值下采样和平均值下采样。如果池化窗口维度是k×k，那么最大值池化输出为该k×k区域的最大值，平均值池化输出该k×k区域的平均值。通过池化操作，特征图的分辨率减小，并且给特征引入了平移与旋转不变性［1］，这使得模型更具鲁棒性。

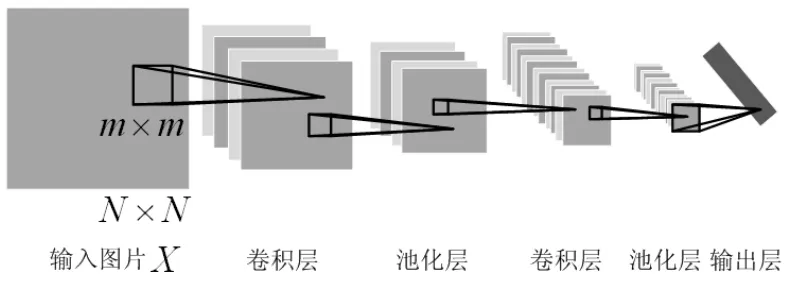
图1　卷积神经网络

图中输入图片大小N×N，第一层卷积核大小m× m；经过第一次卷积运算生成大小为（N-m+1）×（N-m+ 1）的特征图；第一层池化窗口大小k×k，经池化下采样后输出的特征图大小为第二层卷积和池化进行同样的操作。

2　PCANet

卷积神经网络的卷积核作为特征提取器，通常采用随机初始化，再通过反向迭代算法修正更新的方法获得［4］。近年来受深度学习理论影响，Ng.Y等人使用RBM预训练得到卷积核［5］。与之相对地，J.Bruna等人使用小波函数作为一组固定的卷积核［6］，也取得了较好的效果。而马毅等人所设计的PCANet结构更简单，能适应不同数据和问题，成为了深度学习图像分类问题的基线实验［2］。

从结构上看，PCANet是一个三层线性网络，前两层为PCA基向量的计算和卷积计算特征图，第三层是一个输出层。如图2所示。下面将分层详细介绍PCANet。

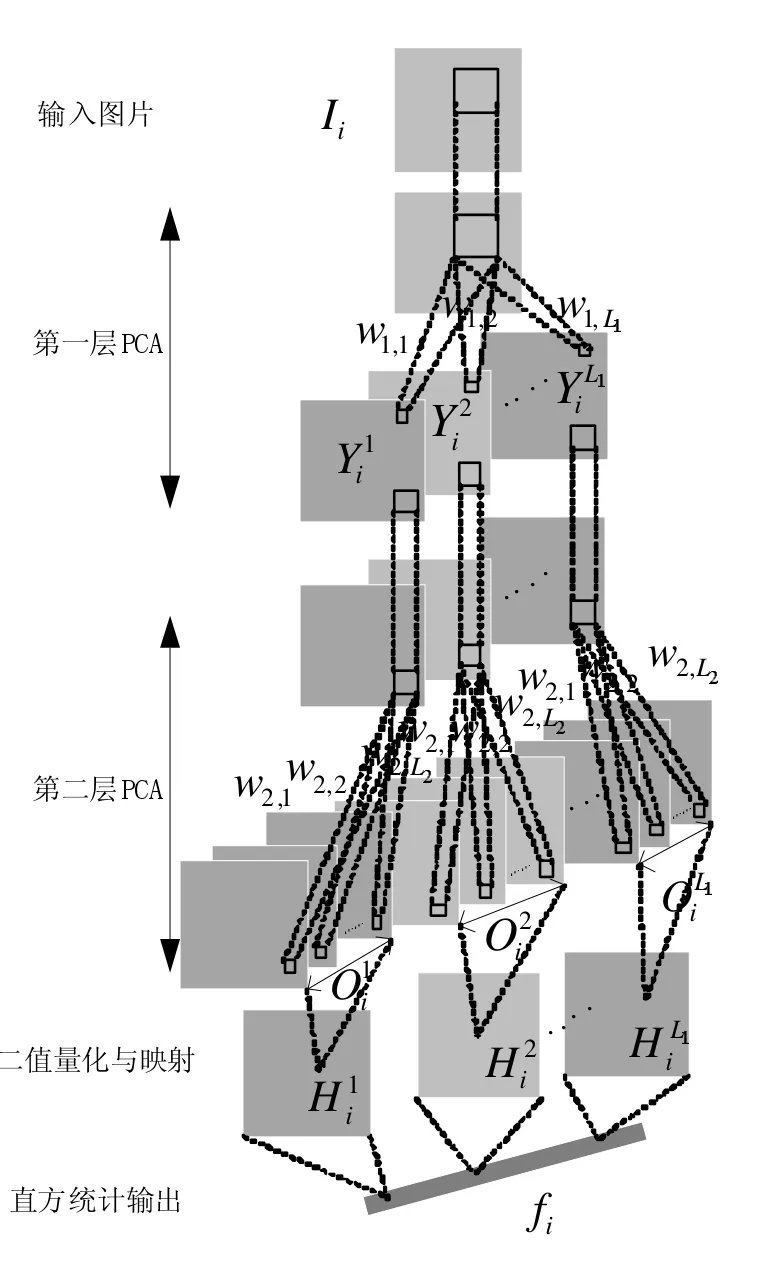
图2　PCANet

输入图片Ii是训练数据集中的第i张图片，经过第一层PCA网络的L1个卷积核w1，1…w1，L1，产生第一层特征图每张特征图经过L2个第二层卷积核w2，1…w2，L2生成一组输出，记为O1i…OLi1；经过二值量化与映射为整图H1i…HLi1，最后直方统计为向量fi作为最终输出。

2.1第一层PCA

PCANet的第一层网络首先利用数据集中的样本离线计算PCA基向量，之后利用这些PCA基向量作为卷积核，对输入图片计算特征。

离线计算PCA基向量的过程如下：对于所有的输入图片，首先进行分片操作，找出所有像素点位置处的小片，在这些小片集合上计算出PCA基向量，小片大小即卷积核大小。对于N张大小为m×n的输入图片集合｛I｝Ni=1，小片大小k1×k2，滑动窗口遍历所有图像获得小片集合，并将每个小片分别展开为一个k1k2维向量，得到xi，1，xi，2，...，xi，m'n'∈Rk1k2，其中xi，j表示第i张输入图片的第j个位置处的小片展成的向量；对于步长为1的滑动窗口遍历，一张输入图片可以提取m'n'个小片，其中，m'=m-「k1/2⌉，n'=n-「k1/2⌉。通过去均值，构建出数据集中所有小片展成向量组成的矩阵∈Rk1k2×Nm'n'作为数据矩阵，其中一层网络的PCA基向量是数据矩阵X的协方差矩阵XXT的特征向量。记w1，i为第i个特征向量，下标1表示第一层网络，则W1=［w1，1，w1，2，…，w1，L1］为第一层网络中XXT前L1个主特征向量组成的矩阵。

在PCA基向量计算结束后，PCANet进入第一层的特征提取阶段。每一个特征向量作为一个卷积核，在输入图片上滑动做卷积运算，生成特征图。其中，第l个卷积核对第i张图片所产生的特征图为：

2.2第二层PCA

第二层网络与第一层结构相同，也经过计算PCA基向量和卷积特征提取两步。

第二层网络的输入是上层卷积得到的所有特征图Yli。PCANet使用同样的分片和去均值操作，计算第二层PCA基向量。将Yli分片，去均值并向量化，写成矩阵形式，得到其中表示在特征图Yli的第j位置处小片所展成的向量去均值的结果。对于第l个卷积核，记经过它卷积产生的所有N张特征图的分片向量集合为矩阵将所有L1个核经过卷积、分片、去均值后的结果连接，可得到数据矩阵Z=［Z1，Z2，…，ZL1］。对数据矩阵Z做PCA分析，即计算ZZT的特征向量，获得第二层网络的卷积核，记为W2=［w2，1，w2，2，…，w2，L2］，其中w2，L2为ZZT的第L2个特征向量，下标2表示第二层网络。

在得到第二层L2个卷积核之后，PCANet开始第二层的特征提取。对于每张由上层网络产生的特征图Yli1，经第二层L2个卷积核的卷积输出为对应到最初的一张原始输入图片，经过两层PCANet网络共产生了L1L2张特征图。

2.3输出层

PCANet的输出层将特征图片做了二进制哈系运算，并转化成直方图统计向量，作为最终输出。

对于最初输入的一张图片，第一层网络首先将其转为L1张特征图，每张特征图经第二层网络又转为L2张特征图。首先对这L2张图经过Heaviside阶越函数进行二值化，然后对这L2张二值图，将每个相同位置像素点的值视为一个L2位二进制数中的一位，于是L2张二值图可转为一张整数图，记为Hli，表示第i张输入图片的第l张第一层特征图生成的整数图，其值域为［0，2L2-1］。将这张整数图平均分为B个块，在每个块上统计［0，2L2-1］中每个整数出现的次数，输出为一个2L2维的向量。对于一张原始输入图片，经过两层网络以及二进制哈希和分块直方图统计运算之后，输出的特征向量为：

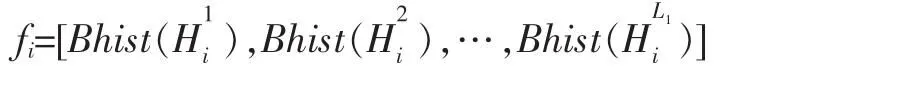
其中Bhist（）为分块统计直方图并将结果展成向量的算子。

3　稀疏PCA网络

PCANet所使用的卷积核是一组PCA基向量，所以经卷积计算得到特征图是基于PCA词典的表达系数。受到这一启示，我们通过构建过完备词典而得到了输入图片的稀疏表达，利用过完备词典更好的表达图第片的局部细节。通常，我们可以使用KSVD来计算过完备词典［7］，然而M.Elad等人证明使用过完备词典的稀疏编码是不稳定的［9］。因此，我们利用了图片的非局部特征［10］，从图像自身特点出发，通过对小图像片聚类，将不同类型的图片组成一个集合，对每个集合计算PCA基向量，构建过完备词典，从而使图像片能够被稀疏表达。聚类与词典构建是稀疏PCA网络的预训练步骤，如图3所示。

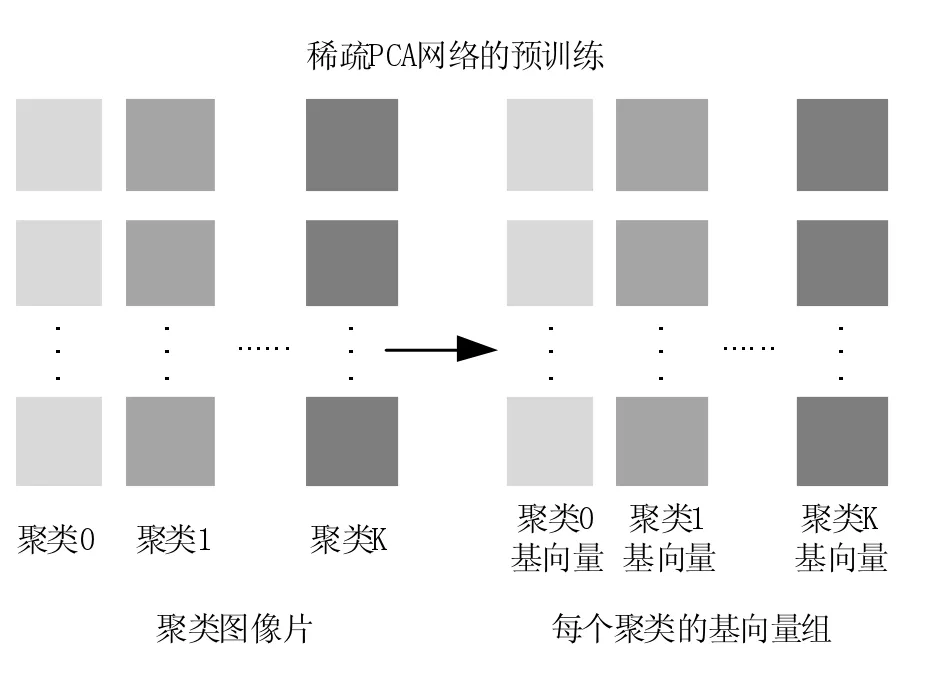
图3　稀疏PCA网络的预训练

分为图像片聚类和聚类PCA基向量计算两步。

3.1图像片聚类

为了将不同类型的小图像片聚类在一起，我们没有使用图像本身的灰度值或RGB值，而是先对图像进行高通滤波，提取出纹理特征，在高频图像域对图像片聚类。这是因为，高频滤波器可以在低层次图像处理中增强有意义的特征［8］。通常，这种对于高频图像片的聚类方法应用与低层次的图像恢复问题中［11］，以学习到更好的词典来表达出局部特征。在卷积神经网络里，卷积核即是词典，因此我们将这种低层次图像处理方法应用于使用卷积神经网络进行的图像分类问题中。

对于灰度图，我们直接在灰度域上进行高通滤波；对于RGB图像，首先我们将其转为YCbCr图像，只取亮度域通道，对其进行高通滤波。图4是一组原始图片，YCbCr亮度域图片以及高频图片的对比。可以看到，经过亮度通道高频滤波之后，图像的纹理，边缘特征被突显出来。将所有图片做这种转换，并提取出每个像素点位置处的小片。

图4　高频滤波特征突显

图中第一列为RGB图像，第二列为YCbCr亮度域图像，第三列为亮度通道高通滤波后的图像，纹理特征突出。

在小片集合中，首先过滤掉所有光滑片，光滑片的选取准则是设定阈值，如果小片的方差小于这个阈值则认为它是光滑片。这样做是为了保留下具有纹理和边缘等特征的片。之后，在剩余的片中，使用K-means聚类方法，将小片聚为K类，这样可使得具有相似特征和结构的小片聚为一类。将过滤掉的光滑小片记为第0类，则所有的小片被聚为K+1，表示如下：

｛Patches0，Patches1，...，PatchesK｝

3.2构建过完备词典

对于光滑片组成的第0类，使用一组固定的DCT基作为其对应的词典；对于其他的非光滑小片集合，分别对应聚类中的小片集合计算它们的PCA基向量，作为对应的词典。对于大小为k1×k2的图像片，我们取前M个基向量，因此可以将词典表示为：

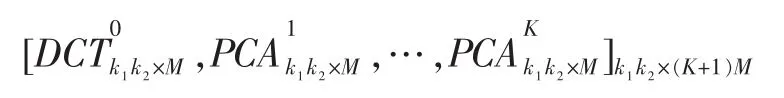
其中DCT0是k1k2×M维的矩阵，表示光滑图片对应的一组DCT基向量。PCAj是k1k2×M的矩阵，表示第j类小图像片的PCA基向量。

3.3卷积核自适应与稀疏表达

小图像片的聚类和过完备词典构建是稀疏PCA网络的预训练步骤。经过预训练后，对于一张输入图片，首先找到所有位置处的小片，对每个片，在KMeans计算出的K个聚类中心中寻找最近的中心，找到所属的类。属于同一类的图像片具有相似的特征，因此我们从过完备词典中选择该聚类对应的基向量作为一组卷积核。如果该小图像片属于第j类，那么此时自适应选择的词典为：

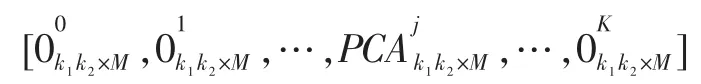
其中0k1k2×M为k1k2×M的全0矩阵。

将这个词典作为卷积核与小片做卷积运算，得到的表达系数为：

我们只取对应的第j组卷积核计算出的表达系数放入特征图的对应位置。稀疏PCA网络的结构如图5所示。

4　图像分类实验

在图像分类实验里，稀疏PCA网络作为一个特征提取器，为最终的分类器提供输入特征。我们使用了CIFAR 10物体分类数据集的子集，来和几种结构相似，并在图像分类国际比赛中获得较好成绩的神经网络模型［12］：PCANet，ConvNet［13］，ScatNet［6］以及一个22层的深层网络GoogLeNet［14］进行实验对比。其中，Goog-LeNet使用softmax分类器，其他模型均使用线性SVM作为分类器。

实验表明，稀疏PCA网络作为PCANet的改进，对于小样本数据集，实验结果在识别错误率上有了下降，并且在训练时间和错误率上均优于复杂的深层网络。

4.1实验数据集：CIFAR 10

CIFAR 10是一个用于物体识别的彩色RGB图片数据集［15］，共包含10个类别，由50000张训练图片和10000张测试图片组成。其中，每张图片是一个维度为32×32的RGB图片。图6是CIFAR 10部分样例。

我们对CIFAR 10数据集进行采样，保留了10种类别图片的数量比例，构建出包含1000张训练图片和1000张测试图片的小样本数据集。

输入图片Ii上的每个小图像片将会被划分到一个聚类中，随后使用该聚类的PCA基向量p1，1…p1，L1作为卷积核进行第一层卷积运算。

4.2参数设置

实验中使用了和PCANet一样的网络层数以及卷积核个数，即两层网络，第一层40个卷积核，第二层8个卷积核，小图像片大小为5×5。在预训练阶段使用KMeans将小图像片聚为两类。训练过程中，每个小图像片将自适应地在两组PCA基向量中选择卷积核。图7为使用K-means聚类出的两个类小图像片计算得到的PCA基向量，即第一层网络的卷积核。

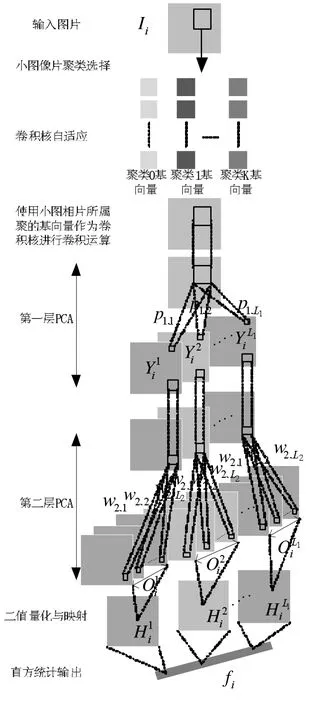
图5　稀疏PCA网络

图6　CIFAR 10彩色图片分类数据集数据示例图中的三列图片分别属于car，ship，cat类

图7　

4.3实验结果比对

使用CIFAR 10采样得到的子数据集，分别在稀疏PCA网络，PCANet，ScatNet，22层的GoogLeNet和一个3层的ConvNet上进行训练。实验结果使用错误率作为评判标准。我们所使用的计算机CPU为主频1.7GHz的Intel Core i5。

各模型的识别错误率如表1所示，训练与测试总时间如表2所示。可以看到，稀疏PCA网络在相同训练集和测试集的情况下，获得了最低的错误率。由于GooLeNet是一个22层的深层网络，在数据集规模较小的情况下容易陷入过拟合，使得错误率较高。在运行时间方面，ConvNet使用反向传播算法不迭代修正卷积核，需要大量时间训练；稀疏PCA网络和PCANet运行时间基本相当；相比ScatNet，由于稀疏PCA网络和PCANet使用了简单的PCA基向量作为卷积核，训练时间相对更少。

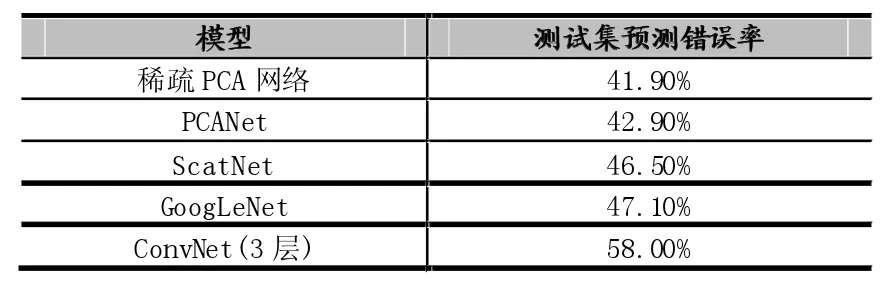
表1　各模型在CIFAR 10子集上的识别错误率

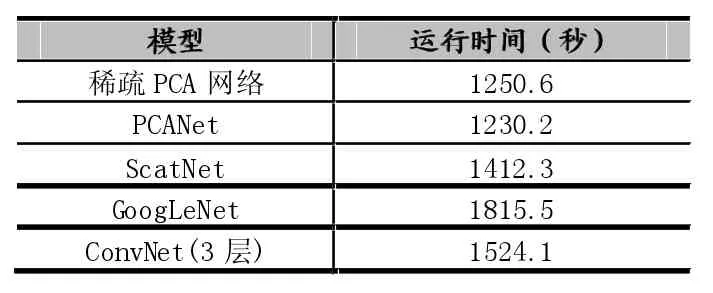
表2　各模型在CIFAR 10子集上的训练与测试运行时间

5　结语

稀疏PCA网络是PCANet的改进，是一种利用图片相似性聚类，进行特征稀疏表达的核自适应卷积神经网络。经实验证实，稀疏PCA网络在图像分类实验上可获得比结构类似的模型更低的错误率，并在训练时间上远小于深层神经网络。

［1］LeCun.Y，Bengio，Yoshua.Convolutional Networks for Images，Speech，and Time Series［M］.The Handbook of Brain Theory and Neural networks，Michael A.Arbib（Ed.）.MIT Press，1998，3361（10）：255-258.

［2］Chan.T.H，Jia.K，Gao.S，Lu.J，Zeng.Z，Ma.Y，PCANet：A Simple Deep Learning Baseline for Image Classification［J］.IEEE Transactions on Image Processing，2015，24（12）：5017-5032.

［3］Alex.K，Sutskever，Ilya，Geoffrey E.H.ImageNet Classification with Deep Convolutional Neural Networks［C］.Advances in Neural Information Processing Systems 25，Curran Associates，Inc.2012：1097-1105.

［4］LeCun.Y，Boser.B，Denker.J.S，Henderson.D，Howard.R.E.Backpropagation Applied to Handwritten Zip Code Recognition［J］. Neural Computation，1989，1（4）：541-551，.

［5］Lee.H，Grosse.R，Ranganath.R，Ng.Y.Convolutional Deep Belief Networks for Scalable Unsupervised Learning of Hierarchical Representations［C］.Proceedings of the 26th Annual International Conference on Machine Learning.ACM，New York，NY，USA，2009：609-616.

［6］Bruna.J，Mallat.S，Bacry.E.Intermittent Process Analysis with Scattering Moments［J］.The Annals of Statistics.2013，35（8）：1872-1886.

［7］Aharon.M，Elad.M，Bruckstein.A.K-SVD：An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation［J］. IEEE Transactions on Signal Processing.2006，54（11）：4311-4322.

［8］Freeman，W.T.Example-Based Super-Resolution［J］.Computer Graphics and Applications，IEEE.2002，22（2）：56-65.

［9］Elad.M，Yavneh.I.A Plurality of Sparse Representations Is Better Than the Sparsest One Alone［J］.IEEE Transactions on Information Theory.2009，55（10）：4701-4714.

［10］Dong.W，Zhang.L，Shi.G，Li.X，Nonlocally Centralized Sparse Representation for Image Restoration［J］.IEEE Transactions on Image Processing.2013，22（4）：1620-1630.

［11］Yang.J，Wright.J，Huang.T.S，Ma.Y.Image Super-Resolution Via Sparse Representation［J］.IEEE Transactions on Image Processing.2010，19（11）：2861-2873.

［12］Krizhevsky.A，Hinton，G.Learning Multiple Layers of Features from Tiny Images［D］.Department of Computer Science，University of Toronto.2009

［13］Zeiler，Matthew.D，Fergus.R.Visualizing and Understanding Convolutional Networks［C］.Computer Vision，ECCV 2014，Proceedings，Part I.2014：818-833.

［14］Szegedy.C，Liu.W，Jia.Y，Sermanet.Going Deeper with Convolutions［C］.2015 IEEE Conference on Computer Vision and Pattern Recognition.2015：1-9.

［15］Russakovsky.O，Deng.J，Su.H，Krause.J.ImageNet Large Scale Visual Recognition Challenge［J］.International Journal of Computer Vision.2015，115（3）：211-252.

CNN；PCA；Sparse Representation；Self-Adaptation；Image Classification

Sparse Pcanet：a Kernel Adaptive Convolutional Neural Network

YANG Ling，SI Ning-bo
（School of Information Science and Engineering，Lanzhou University，Lanzhou 730000）

Convolutional Neural Network（CNN）has the ability of training on high dimension data，and it is inherently parallel.Because of this，it is widely used in image problems.Current trend is to train large image dataset on a deep architecture CNN.Different from this，sparse PCANet mainly focus on the designing of convolutional kernels.Traditional ways take a lot of time to train kernels or need to have some knowledge on the feature extracting，sparse PCANet simply uses PCA bases，and by adding a clustering step，the self-adaptive ability and sparse property are introduced in sparse PCANet.In the image classification experiment，sparse PCANet has a better accuracy than the traditional PCANet in image classification experiment，and the result also outperforms other deep learning models.

1007-1423（2016）29-0026-07

10.3969/j.issn.1007-1423.2016.29.006

杨凌（1966-），女，副教授，硕士，甘肃张掖人，兰州大学，研究方向为人工神经网络及非线性电路司宁博（1990-），男，硕士，甘肃平凉人，兰州大学，研究方向为深度学习和图像识别

2016-08-11

2016-09-30