三轴天线数字化标校方法

余庆丰，黄祖军，李玉广，戴戴强

（中国人民解放军总参谋部61764部队，海南 三亚 572000）

三轴天线数字化标校方法

余庆丰，黄祖军，李玉广，戴戴强

（中国人民解放军总参谋部61764部队，海南 三亚 572000）

针对天线系统跟踪精度低的问题，提出三轴天线数字化标校方法。通过分析三轴天线指向角度记录信息，制作误差曲线，并根据误差曲线的走向寻找其中的数学规律，进行数字化标校，实现降低天线系统误差的目的。测试结果表明，该方法较好地实现了误差补偿功能，提高了天线系统跟踪精度。

三轴天线；角度误差；数字化标校；跟踪精度

0 引 言

为消除天线的过顶盲区，达到过顶跟踪的目的，采用三轴天线座是最有效的途径之一［1］。三轴天线自上而下由天线反射体、俯仰轴系组合、方位轴系组合、第三轴系组合，以及驱动减速装置、汇流装置及安全保护装置等组成，是比较常见的卫星跟踪天线［2］。三轴天线是星地通信链路的重要组成部分，其捕获卫星的精准度影响数据的可靠性和稳定性。从测量跟踪天线的工作过程看，目标、电磁波传播的空间、天线和馈线、跟踪接收机、伺服系统、天线转动设备、数据传递、显示及记录设备都是天线测量系统的组成部分，这些部分都可能给角度测量带来误差［3］。误差会直接影响天线的精度和通信数据的误码率。

三轴天线的误差影响因素很多，主要包括零位误差、大盘不水平、电机轴不匹配、重力下垂引起的俯仰误差、电波折射误差等［4-5］。无论是哪一种误差，最终都会表现为天线定位不准，测量角度与实际角度产生偏差。三轴天线零位误差、大盘水平度和光电轴匹配度降低、重力下垂等因素引起的方位误差和俯仰误差，造成天线系统数字引导跟踪精度低，导致天线在个别位置的指向精度无法满足稳定可靠捕获卫星的技术需求，影响卫星数据正常通信［2］。为有效解决问题，本文提出三轴天线数字化标校方法。该方法具有补偿方位角和俯仰角指向误差的功能，提高天线系统跟踪精度，确保卫星数据稳定可靠跟踪通信。

1 三轴天线角度误差修正模型

1.1 设计思路

对三轴天线的指向角度信息记录文件进行分析，并分析三轴天线角度误差曲线特点和误差影响因子，形成三轴天线数字化标校方法。该方法主要是对角度信息进行补偿，使补偿后的新角度信息对星精度更高，满足三轴天线快速可靠捕获卫星的技术需求。

1.2 方位误差数字化标校

1.2.1 方位误差曲线特点。分析三轴天线方位指向误差曲线可发现，误差与天线角度信息有一定的关系。经过5 0圈次的误差曲线分析发现，方位角速度越大，误差偏移量越大，相关性的大小与一些天线的系统误差因素有关，如图1所示。

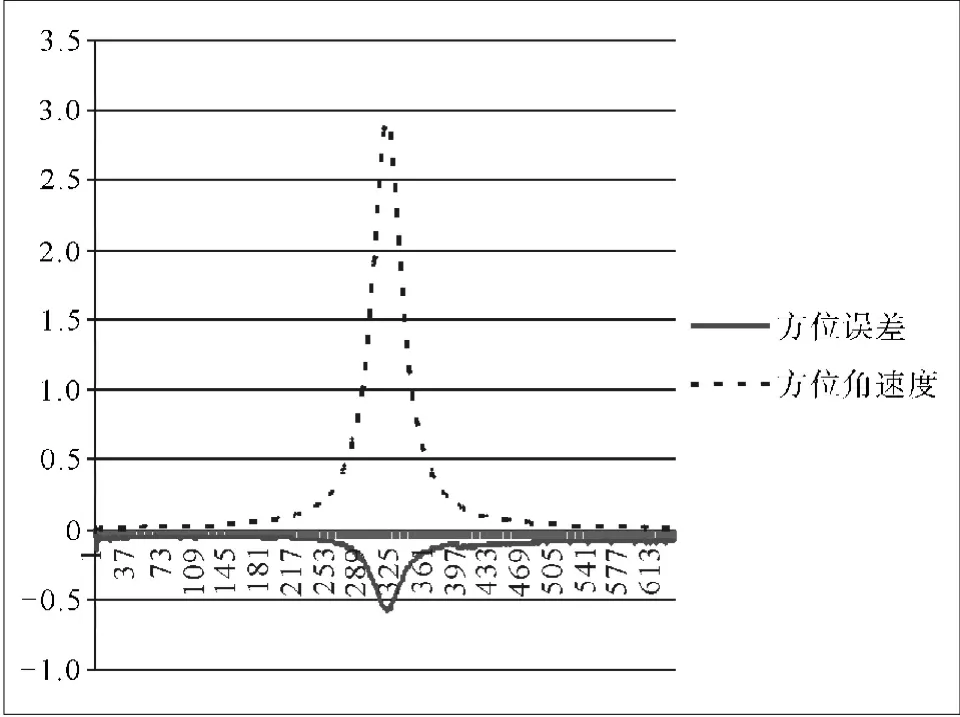
图1 50圈次的三轴天线方位误差曲线和方位角速度曲线

1.2.2 方位误差补偿方法。由1.2.1可知，方位误差与方位角速度存在相关关系，系数为Ka。建立方位误差数字化标校模型为：

其中，A'n为第n秒的方位修正后的角度，An为第n秒的方位引导值，Ka为方位角速度对误差曲线的影响系数，C为偏移量。

计算50圈次的Ka值和C值，进一步分析可发现，K a与倾斜轴角度和最高俯仰角度有关。

（1）当最高俯仰角度小于某度时，Ka=0，C=-0.05。

（2）当最高俯仰角度大于某度时，当第三轴处于某范围内时，Ka=-0.118，C=-0.05；当第三轴处于某范围内时，Ka=0.103，C=-0.05；当第三轴处于某范围内时，Ka=-0.183，C=-0.05。

（3）其他圈次均取Ka=0，C=0。

1.3 俯仰误差数字化标校

1.3.1 俯仰误差曲线特点。分析三轴天线俯仰的指向误差曲线可发现，误差与天线角度信息有一定的关系。对50圈次的误差曲线分析发现，误差曲线的共同点是俯仰轴的误差曲线左端是左高右低近似直线，右端是左低右高，即表示俯仰角度越低，正误差越大，而中间部位与方位角速度直接关联，俯仰误差曲线左右两端进行补偿，使其恢复水平，如图2所示。

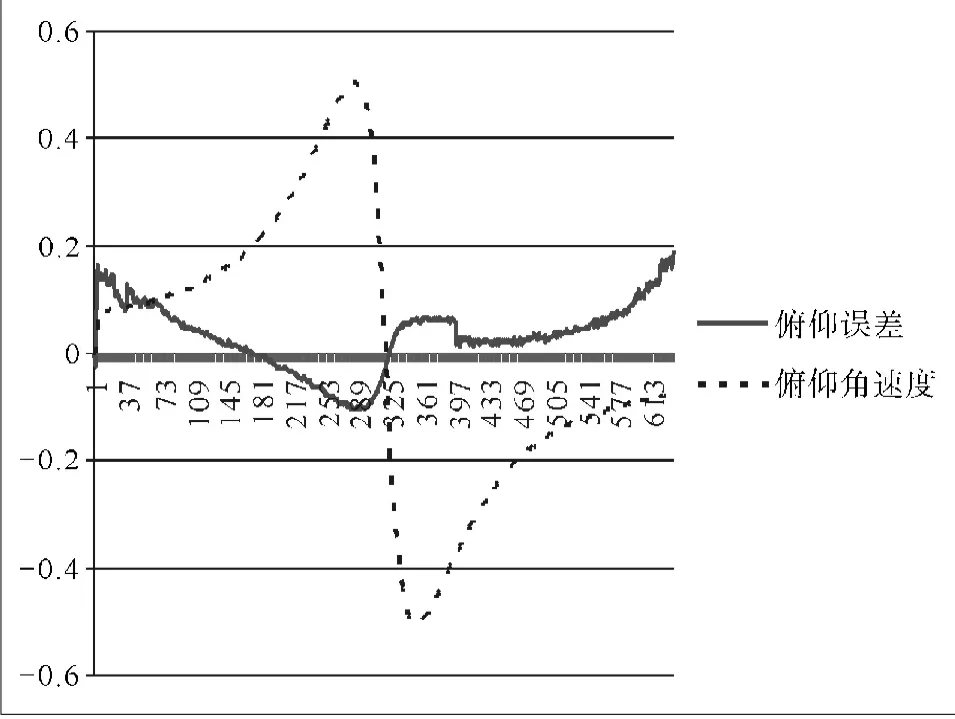
图2 50圈次的三轴天线俯仰误差曲线和俯仰角速度曲线

1.3.2 俯仰误差模型。由1.3.1可知，俯仰误差与俯仰角速度存在相关关系，系数为Ke1。50圈次的三轴天线俯仰误差曲线减去俯仰角速度影响之后的误差曲线，如图3所示。

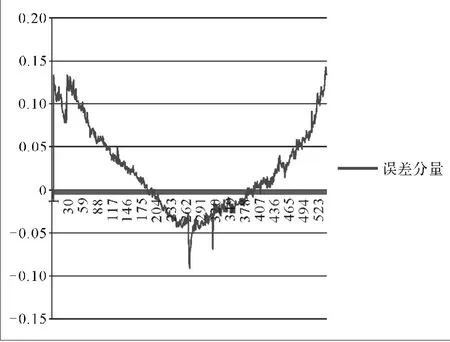
图3 50圈次的三轴天线俯仰误差曲线减去俯仰角速度影响之后的误差曲线

排除俯仰角速度的影响之后，误差曲线变成一个近似抛物线的曲线，采用抛物线去拟合，依抛物线的中点上俯仰最大角度所对应的时间点建立俯仰误差模型为：

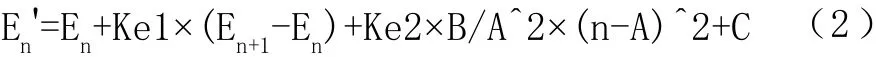
其中，En为第n秒的俯仰角度，A为俯仰最高对应的n值（可在eph文件中查询），Ke1为俯仰角速度对误差曲线的影响系数，Ke2取值为1或0（分别代表误差曲线中有没有包含抛物线曲线），A，B，C均为抛物线的参数。

观察50圈次的抛物线（排除了俯仰角速度影响的误差曲线）之后，形状和特征点基本一致，A由数字引导文件中的俯仰最大角度对应的时间点确定，Ke2的取值为1或0。

计算50圈次的系数。对Ke1值变化曲线进一步分析发现，K e1与第三轴角度和最高俯仰角度有关。

（1）当最高俯仰角度小于某度时，Ke1=0，Ke2=0，B=0，C=0.106。

（2）当最高俯仰角度大于某度时，A可查阅数字引导文件中俯仰角度最大的点对应的时间，B=0.18，C=-0.03。当第三轴处于某范围内时，Ke1=-0.162，Ke2= 1；当第三轴处于某范围内时，Ke1=0.113，Ke2=1；当第三轴处于某范围内时，Ke1=-0.254，Ke2=1；当第三轴处于某范围内时，Ke1=0，Ke2=1；第三轴处于某范围内时，Ke1=0，Ke2=1。

（3）其他圈次均取Ke1=0，Ke2=0，B=0，C=0。

1.4 角度误差修正模型

综合1.2和1.3所述，三轴天线角度误差补偿模型可表示为：

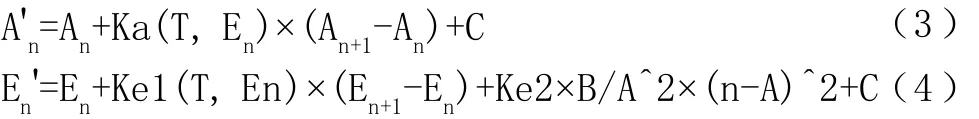
其中，T为天线第三轴角度，A'n为第n秒的方位补偿后的角度，An为第n秒的方位引导值，Ka为方位角速度对方位误差曲线的影响系数（关于天线第三轴角度和俯仰角度的函数），C为偏移量；En'为第n秒的俯仰补偿后的角度，En为第n秒的俯仰引导值，A为俯仰最高对应的n值（可在eph文件中查询），Ke1为俯仰角速度对俯仰误差曲线的影响系数（关于天线第三轴角度和俯仰角度的函数），Ke2取值为1或0（分别代表误差曲线中有没有包含抛物线曲线），B，C均为抛物线的参数。

2 测 试

2.1 单圈次误差修正测试

以单圈次为例进行补偿修正，方位误差和俯仰误差均得到了较大程度的改善。单圈次的三轴天线方位和俯仰修正前后误差曲线比较如图4～图5所示。

2.2 多圈次误差修正测试

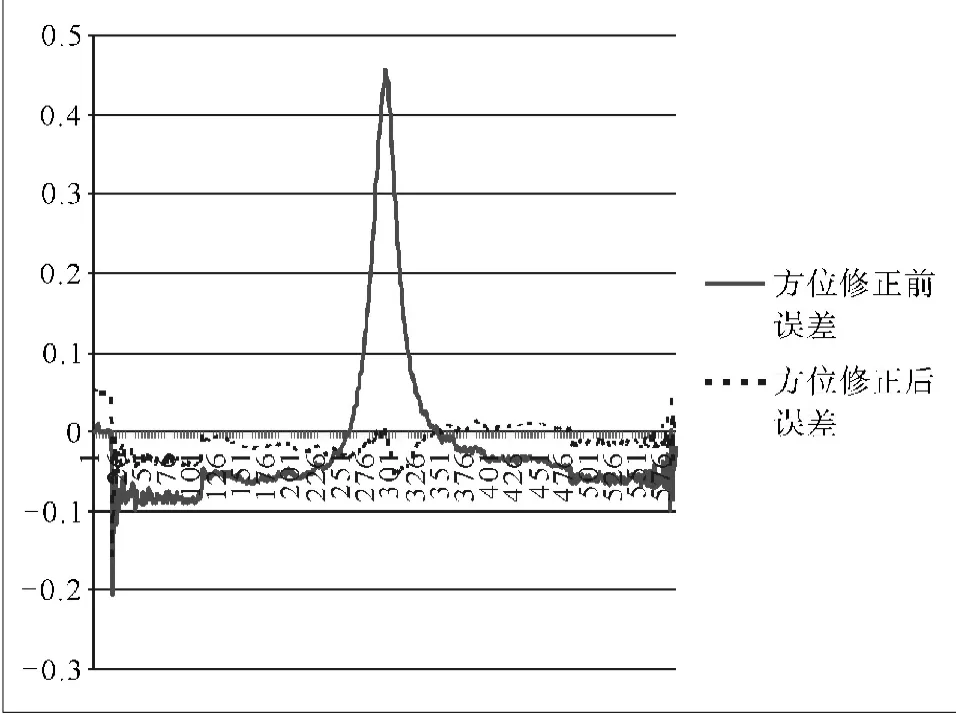
图4 单圈次的三轴天线方位修正前后误差曲线比较

以35圈次为例进行补偿修正，均取得比较好的修正效果，误差值均呈现较大幅度的降低。最大俯仰角度为横坐标，误差值为纵坐标，对35圈次的三轴天线方位修正前后最大绝对误差进行比较，修正后最大绝对误差平均降低了45.6%，修正效果比较明显（见图6）；对35圈次的三轴天线方位修正前后平均绝对误差进行比较，修正后平均绝对误差平均降低了52.2%，修正效果比较明显（见图7）；对35圈次的三轴天线俯仰修正前后最大绝对误差进行比较，修正后最大绝对误差平均降低了61.3%，修正效果比较明显（见图8）；对35圈次的三轴天线俯仰修正前后平均绝对误差进行比较，修正后平均绝对误差平均降低了61.5%，修正效果比较明显（见图9）。

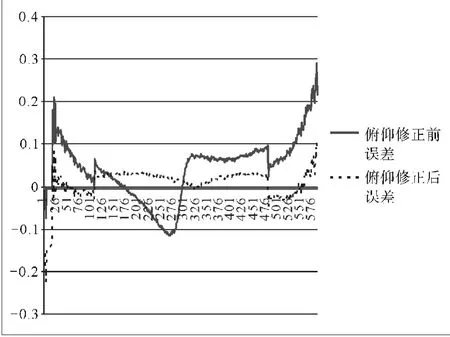
图5 单圈次的三轴天线俯仰修正前后误差曲线比较

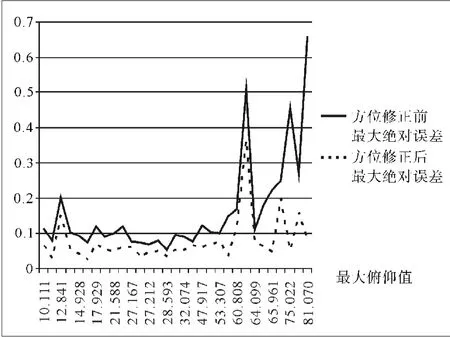
图6 35圈次的三轴天线方位修正前后最大绝对误差比较

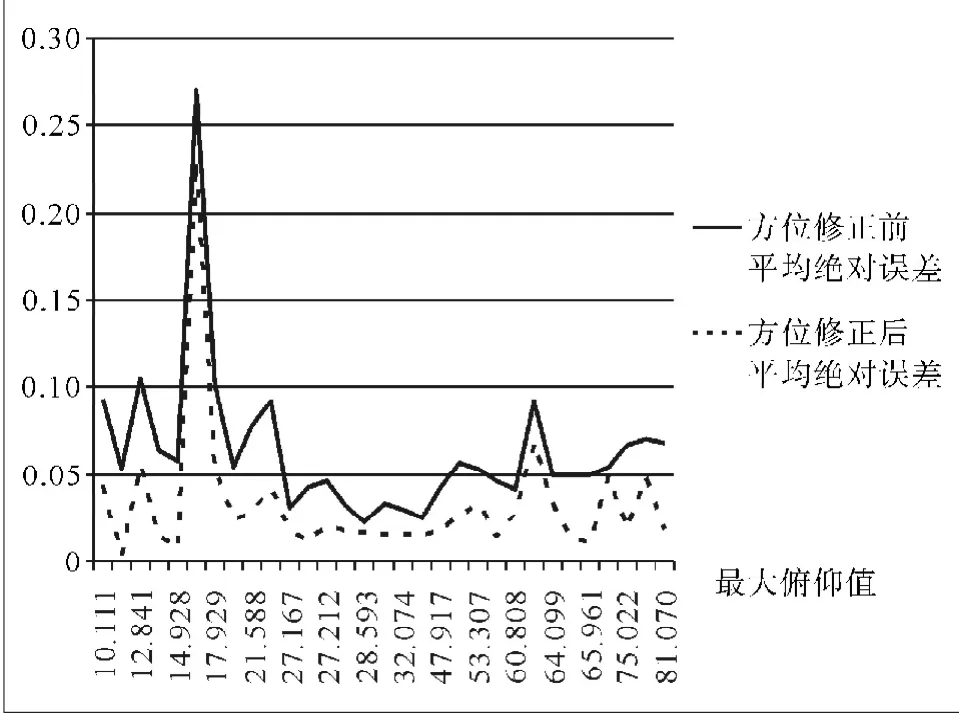
图7 35圈次的三轴天线方位修正前后平均绝对误差比较

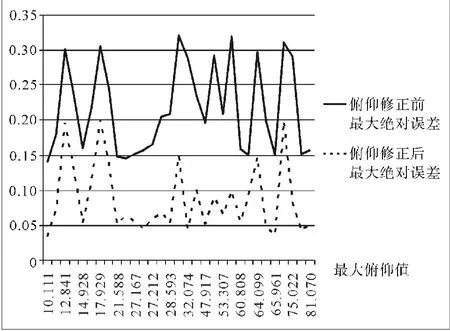
图8 35圈次的三轴天线俯仰修正前后最大绝对误差比较

测试结果表明，三轴天线数字化标校方法能较好地实现误差补偿功能，补偿后其方位和俯仰角度误差大幅度下降，最大绝对误差和平均绝对误差均降低了4 5%以上，补偿效果显著，实现了预期的设计目的。

3 结 论

由于零位误差、大盘不水平、电机轴不匹配、重力下垂引起的俯仰误差、电波折射误差等因素导致天线系统的对星精度降低，导致一些天线无法全程对卫星进行可靠的跟踪，个别位置可能出现丢星现象。因此，提高天线系统指向角度对星的精准度有着重要的意义。对于三轴天线系统，提高天线系统的对星精度常见的方法是星体标校和常规标校等。本文提出的三轴天线数字化标校方法与常见的方法不同，通过分析三轴天线指向角度记录信息，制作误差曲线，并根据曲线的走向，寻找其中的数学规律，进行数字化标校，实现降低天线系统误差的目的。该方法可较好地实现误差补偿功能，应用前景广阔，对其他天线系统误差补偿具有借鉴及指导意义。

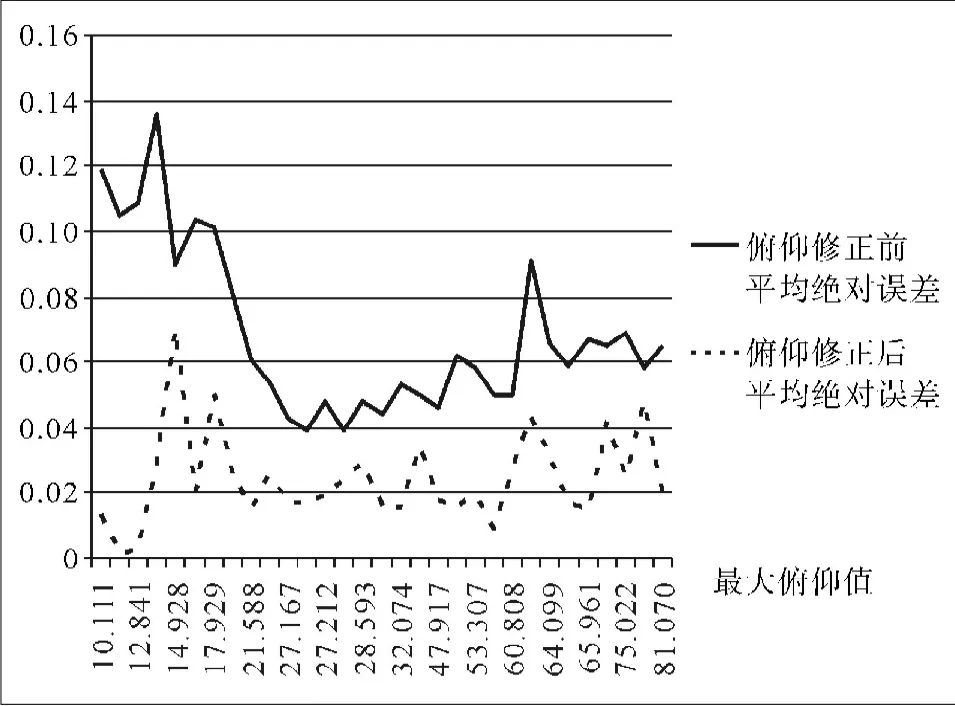
图9 35圈次的三轴天线俯仰修正前后平均绝对误差比较

［1］卓普辉.有关天线过顶跟踪的探讨［J］.电子机械工程，2010，26（3）:43-45.

［2］张腊梅.某地面雷达天线座设计［J］.电子机械工程，2007，23（5）:27-30.

［3］王永华，王万玉.三轴天线角度标校方法［J］.现代电子技术，2014，37（13）:81-84.

［4］王万玉，张宝全，陈刚.俯仰/方位座架轴系误差分析及标校［C］//中国空间科学学会空间探测专业委员会第十九次学术会议论文集:下册.北京:中国空间科学学会空间探测委员会，2006:150-153.

［5］王晶.某型雷达更换天线座底盘误差分析［J］.现代电子技术，2010，33（15）:60-62.

［责任编辑：吴志荣］

Digital Calibration Method of Three-axis Antenna

YU Qingfeng， HUANG Zujun， LI Yuguang， DAI Qiang （61764 Forces of the General Staff Department of the Chinese People's Liberation Army， Sanya， 572000， China）

Digital calibration method of three-axis antenna is recommended considering the low tracking precision of antenna system.It is discussed that error curves can be worked out by analyzing the pointing angle records of the three-axis antenna.And by analyzing the error curve， mathematical rule can be figured out and then the digital calibration can be made in order to diminish errors in antenna system.Test results reveal that this method helps realize the error compensation quite well and improve the tracking precision of antenna system.

Three-axis antenna； Angle errors； Digital calibration； Tracking precision

10.13669/j.cnki.33-1276/z.2016.062

TN820.4

A

1671-4326（2016）03-0057-04

2016-06-04

余庆丰（1988—），男，广东惠来人，中国人民解放军总参谋部61764部队工程师，硕士；

黄祖军（1982—），男，湖南郴州人，中国人民解放军总参谋部61764部队工程师；

李玉广（1983—），男，天津人，中国人民解放军总参谋部61764部队工程师，硕士；

戴戴强（1985—），男，湖南长沙人，中国人民解放军总参谋部61764部队助理工程师，硕士.