人口普查净误差率的估计

丁杨，杜艾卿，胡桂华

（重庆工商大学a.宣传部；b.数学与统计学院，重庆 400067）

人口普查净误差率的估计

丁杨1，杜艾卿2，胡桂华2

（重庆工商大学a.宣传部；b.数学与统计学院，重庆 400067）

人口普查的基本目标是估计其净误差率。以美国为代表的诸多国家通常使用基于配对样本的双系统估计量估计实际人口数，并以它为标准估计人口普查的净误差率。瑞士则通过构造基于非配对样本的普查人口数与实际人口数的比率估计量的方法来估计净误差率。利用实际数据资料和有关公式，瑞士普查局估计了2000年人口普查的净误差率，普查遗漏率和普查错误计数率。实证结果表明，瑞士2000年人口普查计数质量较高。

人口普查；人口普查的质量评估调查；双系统估计量；Jackknife方差估计量

一、引言

人口普查的基本目标是获得某一标准时点上的全国和各个地区以及不同人口统计特征（年龄、性别和城乡等）的人口数目。为了实现这一目标，必须对普查标准时点上的人口进行准确登记。为了评估人口普查人口数目的计数质量，需要在人口普查登记工作结束之后1个月左右，紧跟着再做一次旨在评估人口普查质量的调查[1][2]（事后计数质量评估抽样调查），根据这次调查的结果估计人口普查数目的净误差率[3]。

估计净误差率的经典方法是，先使用事后计数质量评估抽样调查和人口普查这两套配对样本资料构造的基于捕获-再捕获模型的双系统估计量估计实际人口数[4][5]，然后根据公式（实际人口数－普查登记人口数）/实际人口数估计净误差率。目前，美国、乌干达、澳大利亚和中国等国是采用这种经典方法。此前，笔者曾在有关的论文中对经典方法进行了介绍和解读[6][7]。但是，瑞士则是采用了不同于上述经典方法的另外一种路径。那就是，先利用非配对双观察样本资料计算普查人口数与实际人口数的比值，然后用1减去它得到净误差率。本文将详细解读瑞士2000年人口普查质量评估方案的独特思路、缘由和净误差率估计量及其方差估计量的构造。瑞士2010年人口普查质量评估资料尚未对外发布，仍在修改完善中。

构造目标人口总体实际人口数的双系统估计量，从原则上说要求对目标人口总体进行普查登记的名单（E普查名单）和事后计数质量评估再普查追溯性登记名单（P普查名单）对同一个对象进行配对观察[8－10]。当采用抽样调查时，典型的做法是如同美国2000年人口普查质量评估方案那样，以适当的地理小区（例如街区群）为单位抽取样本，然后在样本的每一个地理小区（街区群）中配对获取该地理小区（街区群）的人口普查登记名单（E样本名单）和事后计数质量评估抽样调查追溯性登记名单（P样本名单）。用这种配对获取的两套名单方可寻找二者的重叠部分（即匹配部分）；方可将两套名单的（不含错误计数的）人数连同二名单重叠匹配的人数代入“捕获-再捕获”模型像估计池塘中鱼的数目那样估计目标总体的实际人口数[11]。

然而，瑞士2000年人口普查质量评估方案中的最终样本却并不是如同上面所说的配对样本。在最终样本中，E样本是从初始样本中的“人口普查人口名单抽样框”中抽出来的，而P样本则是从初始样本的“居民建筑物抽样框”中抽出的，因而E样本名单和P样本名单之间不能进行匹配性比对以寻找两个名单之间的重叠部分。至于匹配人数，则是E样本名单和P样本名单分别各自去寻找自己的“配对伙伴”之后各自与自己的“配对伙伴”进行比对得出来的。可见，无法把瑞士2000年方案所得到的数据直接移植到“捕获-再捕获”模型中去构造双系统估计量。或者说，在瑞士2000年方案中所构造的“双系统估计量”是对规范的双系统估计量进行了某种变通性处理以后写出来的。既如此，我们就有必要把这种变通性处理的原因明确地指出来，从而得以做到在基本理论上清楚明晰。

本文的创新性在于：它不是仅仅简单地叙述瑞士2000年人口普查质量评估方案中所设计的工作方法、计算方法，而是深入到方案的背后，讲解作为一个工作方案文件所不可能阐述的，方案中所内蕴的一系列理论问题。由于瑞士2000年与以美国为代表的另外一些国家的人口普查质量评估方案一样，都是运用基于“捕获-再捕获”模型的人口数目双系统估计量来估计人口普查净误差率，但是却循行了与美国[12]等国不同的另外的路径，所以该文把瑞士方案提高到“捕获-再捕获”模型理论与应用体系的高度，在与美国方案的比较研究中来解读瑞士方案[13]，这就使该文远远超出了工作方案推介的层次而进入到理论研究的高级层次。

该文对制订我国2020年人口普查质量评估方案具有重要的参考价值与借鉴意义，能优化或丰富我国人口普查质量评估方法体系。

二、瑞士2000年抽样方案

瑞士2000年抽样方案的基本框架是这样的：以全国为范围，先对邮政区分层，分别在各层用不放还的与抽样单位规模大小成比例的方法抽取邮政区；再在抽取出来的每个邮政区中对邮寄区分层，分别在各层用不放还的与抽样单位规模大小成比例的方法抽取邮寄区；又在抽取出来的每个邮寄区中对建筑物分层，分别在各层用不放还的与抽样单位规模大小成比例的方法抽取建筑物。把经过这样三阶段抽样得到的建筑物样本做为初始样本。

为便于抽取以人为单位的最终样本，对抽取建筑物中的住宅全面调查登记。对每一个住宅，登记的内容包括邮政编码、房间号码、所在街道地址、建筑物编号、建筑物的建筑时间、人口规模等。对住宅中的个人，登记在人口普查标准时点上居住在这个住宅中的人口统计特征信息（年龄、性别、婚姻状况、讲什么语言、公民身份和在普查日和事后计数质量评估抽样调查日期间居住地址是否有变化，等等）。

依据所获得的上述住宅及其个人信息从初始建筑物样本中抽取最终样本。最终样本的抽取路径有两个：一是从依据初始样本建筑物编制的“人口普查人口名单抽样框”中以人为单位使用不重复抽样方法抽取55375人（E样本）；二是先依据抽取的样本建筑物编制“住宅建筑物抽样框”（含建筑物17992个），然后从中使用不重复抽样方法抽取88%的建筑物（15877个），最后把这些抽取建筑物中的所有在质量评估调查中登记的人口全部保留下来作为P样本（共49883人）。

对P样本人口的匹配性比对办法是，与其所在或相邻近住宅建筑物的“普查登记人口名单”进行比对。比对结果可能是：①匹配，即在“普查登记人口名单”中找到了与其相同的人口；②未匹配，即未在“普查登记人口名单”中找到了与其相同的人口；③悬而未决，即是否能在“普查登记人口名单”中找到与其相同的人口还需要进一步收集其他相关信息才能确定；④须从P样本中剔除，即不属于P样本范围内的人口。对悬而未决人口数按匹配人口数或未匹配人口数占匹配和未匹配人口总数的比例在匹配人口数和未匹配人口数之间进行分配。

对E样本人口的匹配性比对办法是，与其所在住宅建筑物的在初始样本抽出之时编制的“质量评估调查登记人口名单”进行比对。比对的结果可能有三种：①在人口普查中正确计数，即E样本中的这个人与本小区“质量评估调查登记人口名单”匹配，或者虽然未匹配但在后续调查中确认该人是普查中的一个正确计数；②在人口普查中错误计数，即E样本中的这个人被证实是普查地址登记错误、重复登记、宠物被当作人登记，等等；③悬而未决，即E样本中的这个人是普查正确计数还是普查错误计数还需要其他有关信息才能确定。对悬而未决人口数按普查正确计数人数或普查错误计数人数占它们两者之和的比例在它们之间进行分配。

由于瑞士方案中所构造的估计量也属于双系统估计量范畴，因此也须如美国方案中的双系统估计量一样，遵循在登记概率相同的人口总体中构造估计量的原则。为此，分别对“普查资料样本”和“事后质量抽样调查资料样本”中的各个个人按照事先选定的与登记概率有关的若干标志进行抽样后分层（今后用层标v表示一个事后层）。

同美国、中国等国方案相比，瑞士方案的抽样设计有两个明显的特点：一是最终样本的样本单位级别低（建筑物和个人，美国街区群，我国是普查小区）；二是分别独立抽取“普查资料样本”和“事后质量抽样调查资料样本”（我国和美国对这两套资料是用配对样本的方式来观测的）。由于上述二个特点，所以瑞士方案估计量及其方差估计量的构造与美国、中国等国不同。

三、普查净误差率估计量及其方差估计

（一）第v事后层实际人口数及其他估计量

为便于说明问题，先考虑直接用配对初始样本构造估计量的情形，然后再考察进一步抽取独立次级样本以后发生了什么变化。为了区别这两种情况，凡是有关配对初始样本的数据记号，一律在它的右上角加注角标mis，它们是matched initial sample（配对初始样本）每个单词的第一个字母；凡是有关独立次级样本的数据记号，一律在它的右上角加注角标iss，它们是independent second-stage sample（独立次级样本）每个单词的第一个字母。

先假设一个拥有总体全面调查人口登记名单的场景：假设拥有对瑞士全国人口进行普查登记的全面名单（E普查名单）和对瑞士全国人口进行事后计数质量评估再普查追溯性登记的全面名单（P普查名单），并且用性别、年龄、所讲的语言和公民身份等标志对名单中的人口进行交叉分层划分成了121个交叉层（v层）。现在把第v层中正确进行普查登记的人数记做，把v层中进行事后计数质量评估再普查追溯普查时点居民的登记人数记做，把两个登记之间匹配的人数记做CEv，则瑞士全国人口总体中第v层实际人口数的双系统估计量为：

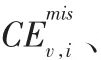
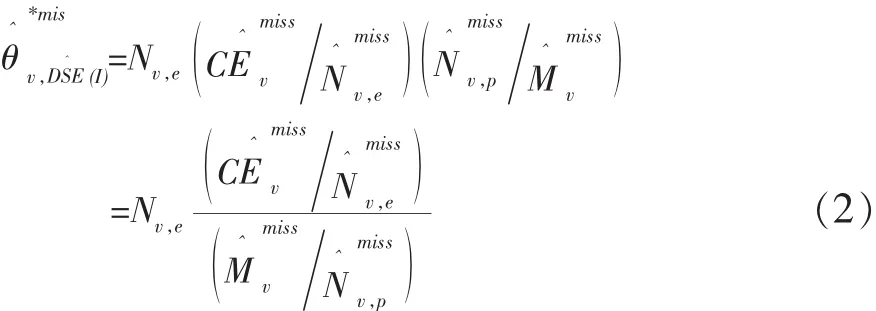
现在来定义总体的两个比率指标。其一，定义：

为v层总体普查正确登记率，它是人口普查登记名单中正确登记人数与全部登记人数的比率，相应地，1－Rv，ce为人口普查的错误登记率；其二，定义：

式（4）为v层总体事后计数质量评估再普查登记与普查登记的匹配率，它是事后计数质量评估再普查追溯登记名单中与普查登记匹配的人数与事后计数质量评估再普查追溯登记名单人数的比率，相应地，1-Rv，m为事后计数质量评估再普查登记与普查登记的未匹配率。这里有必要强调的是，联合国、瑞士、美国、英国、乌干达、南非和中国等均是把1-Rv，m叫做为人口普查的遗漏率。其理由是，1-Rv，m的分母是事后计数质量评估再普查登记的人口数，分子是事后计数质量评估再普查中进行了登记但人口普查却将其遗漏的人口数。但本文认为，这样做的缺陷有二：一是1-Rv，m的分子和分目都缺少了同时被普查和事后计数质量评估再普查遗漏的人口数；二是无法保持平衡关系式，即人口普查的净误差率等于普查遗漏率与普查错误登记率之差（净误差率的分母是目标人口总体的实际人口数），例如，瑞士2000年普查净误差率、普查遗漏率和普查错误登记率分别为1.41%、1.64%和0.35%。

此外，还要将式（4）与式（3）相比再定义一个比率指标（它将在稍过些时候用到）：

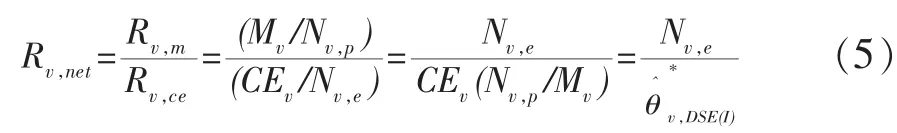
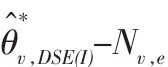
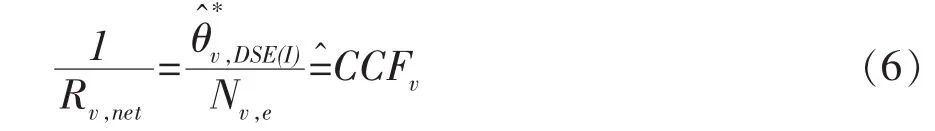
CCFv称做人口普查数字修正因子。

现在回到式（2）。我们看到，式（2）中的两个比率可以分别充当式（3）和式（4）的估计量，即，首先，

可作为式（3）的估计量，这个估计量是用配对样本中各邮政区的人口普查登记名单（E样本名单）资料构造的；其次，

可作为式（4）的估计量，这个估计量是用配对样本中各邮政区的事后质量抽样调查追溯性登记名单（P样本名单）以及它与配对样本中各邮政区的人口普查登记名单（E样本名单）相匹配部分的资料构造的。

请注意，式（7）、式（8）以及式（2）是在假定对邮政区样本进行配对观察的场景下写出来的。然而，实际情况是，在瑞士2000年方案中，邮政区样本只不过是抽样调查的初始样本，在初始样本的基础上又进一步抽取了最终样本。即，一方面从初始样本的人口普查登记名单中抽取了一个人口样本当做E样本；另一方面从初始样本的住宅建筑物名单中抽取了一个住宅建筑物样本，再通过对这些住宅建筑物中的人口进行观察登记形成了一个P样本。面对手中所掌握的此种最终样本，瑞士2000年方案采取了一个关键的措施：变更式（3）和式（4）的估计量。即，不使用对邮政区样本进行配对观察场景下的式（7）和式（8），而改为用手中所掌握的最终样本去为式（3）和式（4）构造新的估计量。它们是：其一，用

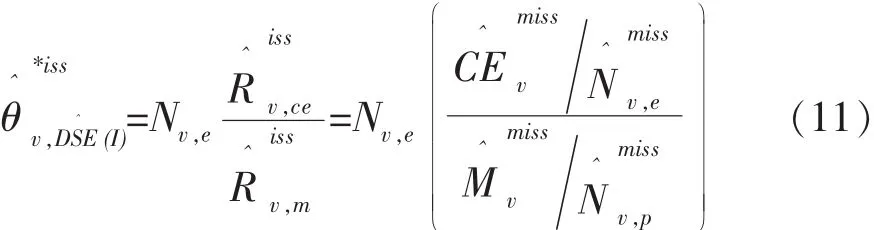
下面对式（11）中的两个比率进行说明。

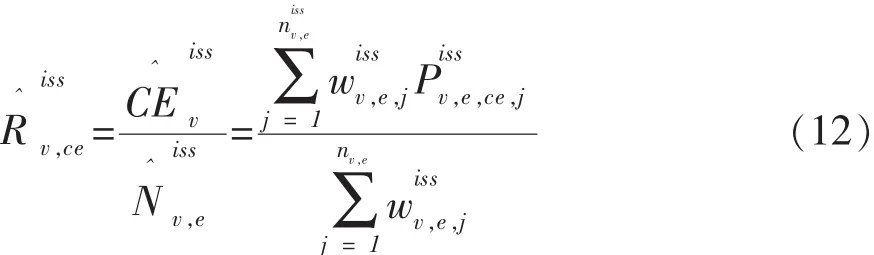
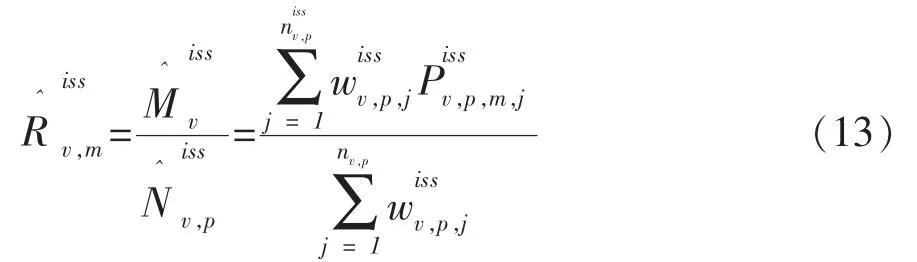
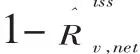
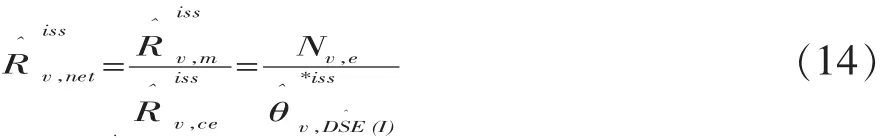
在瑞士2000年方案中采用了以人为抽样单位的次级样本获取E样本的有关数据，这与使用住宅建筑物次级样本去获得E样本的有关数据相比，方案中所采用的抽样策略可能会使估计量的精度有所得益。

（二）行政区域人口数估计量

行政区域指的是全国或是其它级别的行政区（如城市）。行政区是或大或小的地理区域。在前面所划分的各个v层，可以是针对全国范围的，也可以是针对某一个其他级别的行政区的。

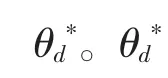
式（15）中，由下面的式（16）计算。即

（三）全国实际人口数、净误差率估计量及其方差估计

为此，先要给出全国普查人口数与实际人口数比值Rnet的定义。这可以仿照式（5）来完成，即定义：

由式（14）和式（16）知，在v层有：

于是，假定在不划分v层的全国相应地有：

由式（19）写出

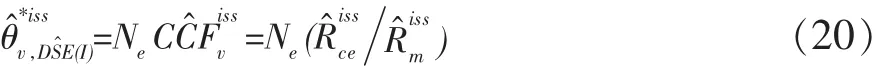
用式（20）做为式（17）中分母的估计量，写出的估计量为：

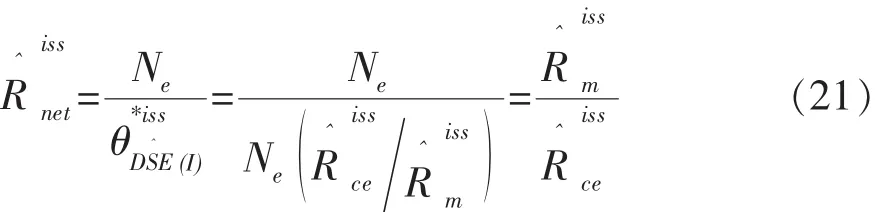
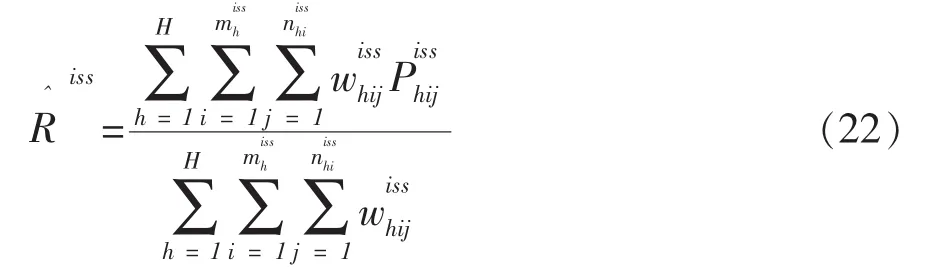
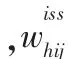
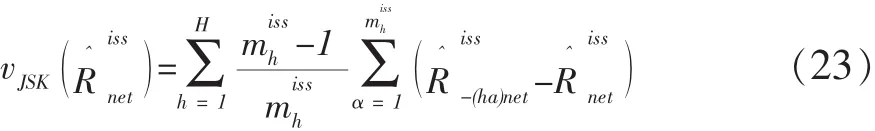
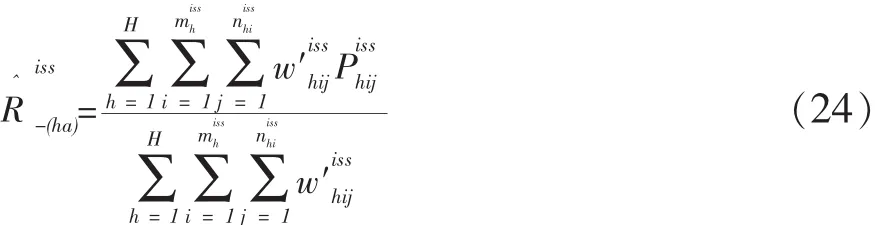
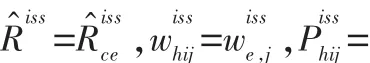
四、实证分析

本文实证数据及结果来源于文献[14]。该文献利用瑞士普查局采集的个人资料和前面的有关公式使用多种统计软件估计了瑞士2000年人口普查的正确计数率、遗漏率和净误差率以及它们的抽样标准差。

由于是第一次进行人口普查质量评估，因而经验不足，于是瑞士普查局在实证分析中从美国聘请了有关的专家指导，也使用了美国提供的统计软件系统。整个估计包括4个基本程序：一是采集数据；二是数据处理；三是估计，包括初步估计和最终估计；四是与美国、英国、澳大利利亚、新西兰估计的人口普查净误差率进行比较。

有关的最终估计结果如表1。

表1 普查正确计数率，匹配率，人口普查数字修正因子，净覆盖和净误差率及它们的标准误差

对表1中的数据，进行如下分析：

第一，总的覆盖率为98.59%，相应的净误差率为1.41%；匹配率为98.4%，遗漏率为1.6%；普查正确计数率为99.65%，普查错误计数率为0.35%。按联合国规定的净误差率标准来看，瑞士2000年人口普查是较为成功的，因为其净误差率在2%以下。另外，遗漏率是错误计数率的约5倍，这说明瑞士2000年人口普查遗漏比重复、地址登记错误等错误计数情况严重。这意味着，在2010年人口普查中要把如何控制遗漏作为普查工作的重点来抓。

第二，从性别来看，男性的净误差率高于女性，而普查正确计数率和匹配率均低于女性，但高于或低于的幅度不大。这一方面说明，男性的普查登记质量不如女性，另一方面也说明，男性净遗漏的人口数多于女性。出现这种状况的主要原因是，男性在普查期间外出的机会多于女性，以及男性在报告自己的个人信息时没有女性那么细心。

第三，从年龄结构来看，净误差率的变动幅度较大。其中，20～31岁组的净误差率最大，为2.84%，而年龄组60～79岁的净误差率最小，为0.82%。这是因为20～31岁组人口外出旅游、学习、出国、经商等机会多于60～79岁年龄组的人口。其他年龄组的净误差率在0.82%～2.84%之间。另外还值得注意的是，20～31岁组的普查正确计数率和匹配率最低，换句话说，普查错误计数率和遗漏率最高。这说明，20～31岁年龄组的普查登记质量最差及遗漏的人口最多，因而是下一次人口普查登记工作关注的重点人群。

第四，从是否为瑞士公民来看，本土瑞士人的遗漏率和净误差率最低，分别为1.28%和0.98%，而居住在瑞士但未获得瑞士永久性资格的外国人的遗漏率和净误差率最高，分别为8.12%和3.48%。出现这种情况的主要原因是，有些外国人在普查期间离开了瑞士，或者对普查不够重视，或受语言水平所限而无法填写普查表。

第五，从婚姻状况来看，单身者普查正确计数率最低（99.50%）和净误差率最高（1.72%），已婚者普查正确计数率最高（99.77%），净误差率最低的是鳏夫的0.79%。这说明婚姻状况影响人们参与普查的态度和质量。单身者流动性大，鳏夫流动性小，这是他们净误差率差异大的根本原因。

第六，从讲的语言来看，讲德语和罗曼什语人口的普查正确计数率最高（99.67%）和净误差率最低（1.28%）。这主要与讲这两种语言的人口占的比例大（72%）有关。讲意大利语人口只占4.3%，他们的普查正确计数率最低（99.47%）。

第七，从人口居住区的范围来看，居住区范围大的净误差率最大（1.77%），其次分别是居住范围小和中等的1.12%和1.02%。一种可能的解释是，人口居住范围大，普查登记难度也大，相应发生遗漏的概率也大。

第八，从城乡来看，一方面，乡村普查正确计数率最高（99.68%），其次分别是城镇和城乡结合地区的99.65%和99.64%；另一方面，乡村的净误差率也最低（1.07%），其次分别是城乡结合部和城镇的1.34%和1.82%。这与乡村人口对普查的重视程度大于城镇和城乡结合部人口有关。换句话说，乡村人口能够积极主动参与人口普查，因而被普查遗漏的概率小。

五、结语

从以上论述可以看出，构造双系统估计量的双系统资料，应当是在一个地理区域“总体”层面上的配对资料。但就瑞士2000年人口普查质量评估调查方案来说，抽取初始样本以后所形成的“质量评估调查登记人口名单”和“普查登记人口名单”属于这种配对资料；但是，分别从“普查登记人口名单抽样框”和“住宅建筑物抽样框”这两个抽样框中独立抽取最终样本后，由这两个最终样本分别形成的“质量评估调查登记人口名单”和“普查登记人口名单”就不再属于上述那种配对资料，因此不能用这两个名单进行匹配性比对，从而也就无法直接构造双系统估计量。所以，瑞士不能通过构造配对双系统资料的双系统估计量估计实际人口和人口普查净误差率，而只能通过非配对双样本估计普查净误差率。

瑞士2000年人口普查质量评估方案涉及的估计量包括普查净误差率估计量、普查遗漏率估计量和普查错误计数率估计量及其方差估计量等。瑞士普查局利用非配对双样本人口资料和这些估计量对2000年瑞士普查的净误差率、普查遗漏率和普查错误计数率进行了估计。本文对估计结果做了分析。分析结果表明，瑞士2000年人口普查质量较高，净误差率1.41%没有超过联合国规定的2%的较好标准。

[1]陈培培，金勇进.对我国人口普查数据质量评估的若干思考[J].现代管理科学，2014（9）：3-5.

[2]贺本岚，金勇进，巩红禹.人口普查事后质量抽查的有关问题：国外经验及借鉴[J].商业经济与管理，2010，227（9）：93-96.

[3]金勇进，张喆.抽样调查中的权数问题[J].统计研究，2014，31（9）：80-84.

[4]陶然，金勇进.普查事后抽查的理论分析与经验启示[J].调研世界，2010（4）9-12.

[5]胡桂华，廖歆.捕获-再捕获模型的统计学原理[J].统计与信息论坛，2012，27（9）：8-13.

[6]胡桂华.人口普查误差刍议[J].统计与信息论坛，2011，26（11）：12－18.

[7]胡桂华.论人口普查质量评估统计量[J].统计与信息论坛，2011，26（4）：3－7.

[8]胡桂华.人口普查覆盖误差估计方法综述[J].统计与信息论坛，2013，28（9）：39－46.

[9]胡桂华，莫锦萍，涂火年.基于捕获-再捕获模型的双系统估计量模型式框架[J].徐州工程学院学报，2012，27（4）：23－29.

[10]胡桂华.行政记录在人口普查质量评估中的应用[J].徐州工程学院学报，2011，26（3）：21-34.

[11]胡桂华.美国2000年和2010年人口普查质量评估方法解读[J].数理统计与管理，2010，29（2）：262-276.

[12]胡桂华.人口普查净误差构成部分的估计[J].统计研究，2011，28（3）：90-100.

[13]U.S.Bureau of the Census.Accuracy and Coverage Evaluation of Census 2000：Design and Methodology[M].Washingtion：U.S.Census Bureau，2004.

[14]Anne Renand.Coverage Estimation for the Swiss Population Census 2000[M].Stockholm：Swiss Federal Statistical Office，2004.

Net Error Rate Estimation for the Population Census

DING Yanga，DU Ai-qingb，HU Gui-huab
（a.Propaganda Department；b.School of Math and Statistics，Chongqing Technology and Business University，Chongqing 400067）

Basic aim for population census is to estimate its net error rate.Many countries represented by America usually use dual system estimator based on matched samples to estimate true population，and to estimate net error rate according to it.Swiss estimates net error rate by means of constructing rate estimator between census population and true populationm based on nomatched samples.Swiss Census Bureau estimated net error rate，omission rate，and erroneous count rate for Swiss population census 2000.The empirical results show that Swiss population cenus 2000 had higher count quality.

Population Census；Quality Assessment Survey for Population Census；Dual System Estimator；J ackknife Variance Estimator

C829.1

A

1007-0672（2016）01-0018-08

2015-05-27

本文获国家社科基金项目“人口普查净误差估计中的三系统估计量研究”（15BTJ011）、国家社科基金项目“我国人口普查质量评估方法研究”（10XTJ003）、教育部人文社会科学研究规划基金项目“行政记录在人口数目估计中的应用研究”（13YJA910004）、全国统计科学研究计划重点项目“多系统模型在人口普查质量评估中的应用”（2012LZ044）、全国统计科学研究计划重点项目“人口行政记录与政府统计：国外经验及启示研究”（2013LX04）、重庆工商大学2014年研究生教育教学改革研究项目（2014YJG021）“统计学专业研究生《政府人口统计调查》课程设置方案研究”资助。

丁杨，女，四川达县人，重庆工商大学宣传部干事，研究方向：学生宣传统计；杜艾卿，男，湖北武汉人，重庆工商大学数学与统计学院助教，研究方向：人口普查质量评估理论与方法；胡桂华，男，湖北武汉人，重庆工商大学数学与统计学院教授，研究方向：人口普查质量评估理论与方法。