抽象函数对称问题的求解与拓展

侯有岐　白丽萍

(陕西省汉中市405学校，723312)



抽象函数对称问题的求解与拓展

侯有岐白丽萍

(陕西省汉中市405学校，723312)

一、引例

2016年全国高考数学文理科试卷中有这样两道题:

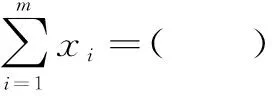
(A)0(B)m(C)2m(D)4m

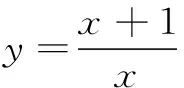
(A)0(B)m(C)2m(D)4m

这两道题貌似接近,实则相去甚远,它们代表了本质上完全不同的两类函数图象的对称问题.

事实上，根据函数图象的概念及对称图形的定义，不难证明以下结论：

推论1若函数y=f(x)定义域为R,且满足条件f(a+x)=f(a-x),则函数y=f(x)的图象关于直线x=a对称.

推论2若函数y=f(x)定义域为R,且满足条件f(x)=f(2a-x)),则函数y=f(x)的图象关于直线x=a对称.

可以看出，函数f(x)满足的条件中x的系数一个为1,另一个为-1时,相应解析式相加除以2,可得y=f(x)图象的对称轴方程.

推论3若函数y=f(x)定义域为R,且满足条件f(a+x)=f(a-x), 又若方程f(x)=0有n个根,则此n个根的和为na.

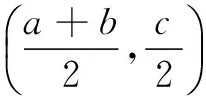
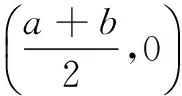
推论2若函数y=f(x)定义域为R,且满足条件f(a+x)+f(a-x)=0(a为常数),则函数y=f(x)的图象关于点(a,0)对称.

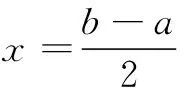
推论1函数y=f(x-a)与函数y=f(a-x)的图象关于直线x=a对称.

推论2函数y=f(a+x)与函数y=f(a-x)的图象关于直线x=0对称.

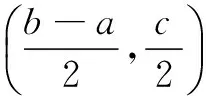
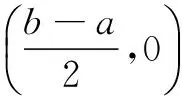
在理解并记忆以上定理及推论时,极易混淆,因而造成很多学生对这两道高考题解答时出错.

二、试题解答

根据上述结论，不难得到上述两道试题的具体解答过程如下：

题1因为y=f(x),y=|x2-2x-3| 都关于x=1对称,所以它们的交点也关于x=1 对称.

因此选B.

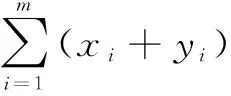
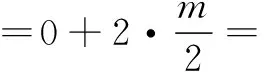
故选B.

三、本质挖掘

常用结论中四个定理的本质完全不同.定理1是探讨一个函数的图象本身关于某条直线的对称的问题,即自身轴对称问题；定理2是探讨一个函数的图象本身关于某点的对称的问题,即自身中心对称问题；定理3是探讨两个函数的图象关于某条直线的对称的问题,即相互轴对称问题；定理4是探讨两个函数的图象关于某点的对称的问题,即相互中心对称问题.解题时要注意它们的区别.

进一步拓展问题，不难证明上述四个定理的更一般形式：

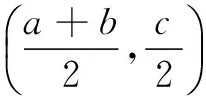
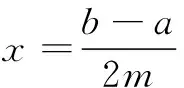
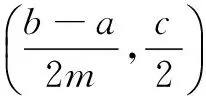
读者不妨自行给出相应证明.