宏细观结合各向异性砂土的变形特性模拟

李学丰， 孔　亮， 袁　琪， 王燕昌

(1. 宁夏大学 物理电气信息学院，宁夏 银川 750021； 2.青岛理工大学 理学院，山东 青岛 266033)



宏细观结合各向异性砂土的变形特性模拟

李学丰1， 孔亮2， 袁琪1， 王燕昌1

(1. 宁夏大学 物理电气信息学院，宁夏 银川 750021； 2.青岛理工大学 理学院，山东 青岛 266033)

采用宏细观结合的方法建立本构模型对各向异性砂土的变形特性进行模拟.该方法用组构张量定义了一新的各向异性状态变量，考虑该变量对临界状态线的影响建立各向异性模型.引入状态变量后，模型的临界状态面和其他状态面都随各向异性程度的不同而偏离静水压力轴，临界状态方程、硬化准则和剪胀方程都是孔隙比、围压、加载模式和各向异性变量的函数，模型用一组参数可以描述不同围压和密度的砂土各向异性强度-变形的力学响应.通过对各向异性砂的强度和含细观特性分析的试验变形模拟，初步验证了模型的合理性.

砂土; 宏细观; 强度; 各向异性

砂土的力学响应与其细观特性紧密相关.天然砂土沉积过程中颗粒定向排列形成了其细观原生各向异性；在主应力方向变化或非比例加载等条件下，导致其细观结构发生了演化，表现出应力诱使各向异性，加剧了土体变形、强度与破坏的复杂性.因此，砂土各向异性深层的机理都可以统一到其细观特性.由于各向异性的普遍性以及它对砂土一些难点问题(如地震液化、循环剪切、应变局部化破坏和非共轴特性等)有显著影响，因此国内许多学者都进行了研究[1-3].Yamada等[4]，Arthur等[5]，Abelev等[6]试验研究表明：在其他条件相同时，大主应力面与沉积面重合时抗剪强度最高，砂土的抗剪强度整体上随大主应力方向角的增大而降低；Oda[7]通过细观观测发现，土体沉积时颗粒长轴定向排列结构在加载后期加载过程中变化甚微，Oda的模型试验也证实，不考虑地基土的强度各向异性可能会导致过高计算地基承载力30%～50%，使工程设计偏于危险.这些理论和试验等现象的根本原因是砂土原生各向异性的存在.

原生各向异性主要的描述方法为：根据原生应力状态和固结历史来定义屈服面与静水压力轴夹角的初始应力状态方法[8]和各向异性张量的方法[9],定义边界面或屈服面的中心点可以随着塑性变形发展而移动的运动硬化方法[10],还有直接从细观颗粒间的作用建立细观结构的描述方法[11],以及用组构张量的描述方法[12-13].然而这些方法都不同程度地存在参数多、参数不易确定和物理意义不明显、数学表述复杂、工程应用复杂等缺点，而且大多数模型只做了定性分析，定量描述比较少.因此，为了更合理地模拟砂土强度和变形特性，本文在以往建立的砂土本构模型[3]和各向异性破坏准则[14]的基础上，将宏细观结合定义的一个新的各向异性状态变量引入本构模型，考虑砂土细观组构和应力状态对模型的临界状态、峰值状态、应力转化状态、剪胀方程和硬化准则的影响建立本构模型.使用Toyoura砂的强度试验结果和结合细观分析的变形试验结果进行模型验证.

1　宏细观结合的各向异性描述特点

组构张量是细观力学确定的内部状态变量，用以表达土体颗粒排列特征的参量，它由材料内在各向异性和密度共同确定.因此基于组构张量研究土体宏观力学关系实质上是一种宏细观结合的方法，详细见文献[14]，这里重点对新定义的各向异性状态变量引入本构模型后的特点进行分析.

1.1各向异性状态变量的定义

宏细观结合方法思路是将细观定义的组构张量和加载应力的单位张量结合，形成一个组合张量，然后用组合张量的不变量定义一个各向异性状态变量，用该变量反映土体细观结构对宏观现象的影响.

组构张量采用Oda等[15-16]定义的形式

(1)

式中：a为可以测量的各向异性参量，其大小表示了土颗粒方向和参考面方向各向异性的程度.

在复杂应力状态下主应力轴相对于土体组构会发生旋转，旋转后组构张量满足以下关系:

(2)

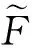
将组构张量和应力张量形成组合张量，用组合张量的两个不变量可定义一个新的各向异性状态变量

(3)

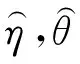
1.2各向异性状态变量的特点

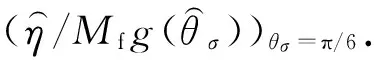
图2a中的基准点也为常规压缩点，图中Mcs=1.25，对于常规三轴压缩点A≡0，各向异性不影响该状态点的强度.从图中可以看出,随组构张量和应力几何关系的变化，各向异性状态变量变化的关系，同样在材料参数确定的基准点计算值为0.

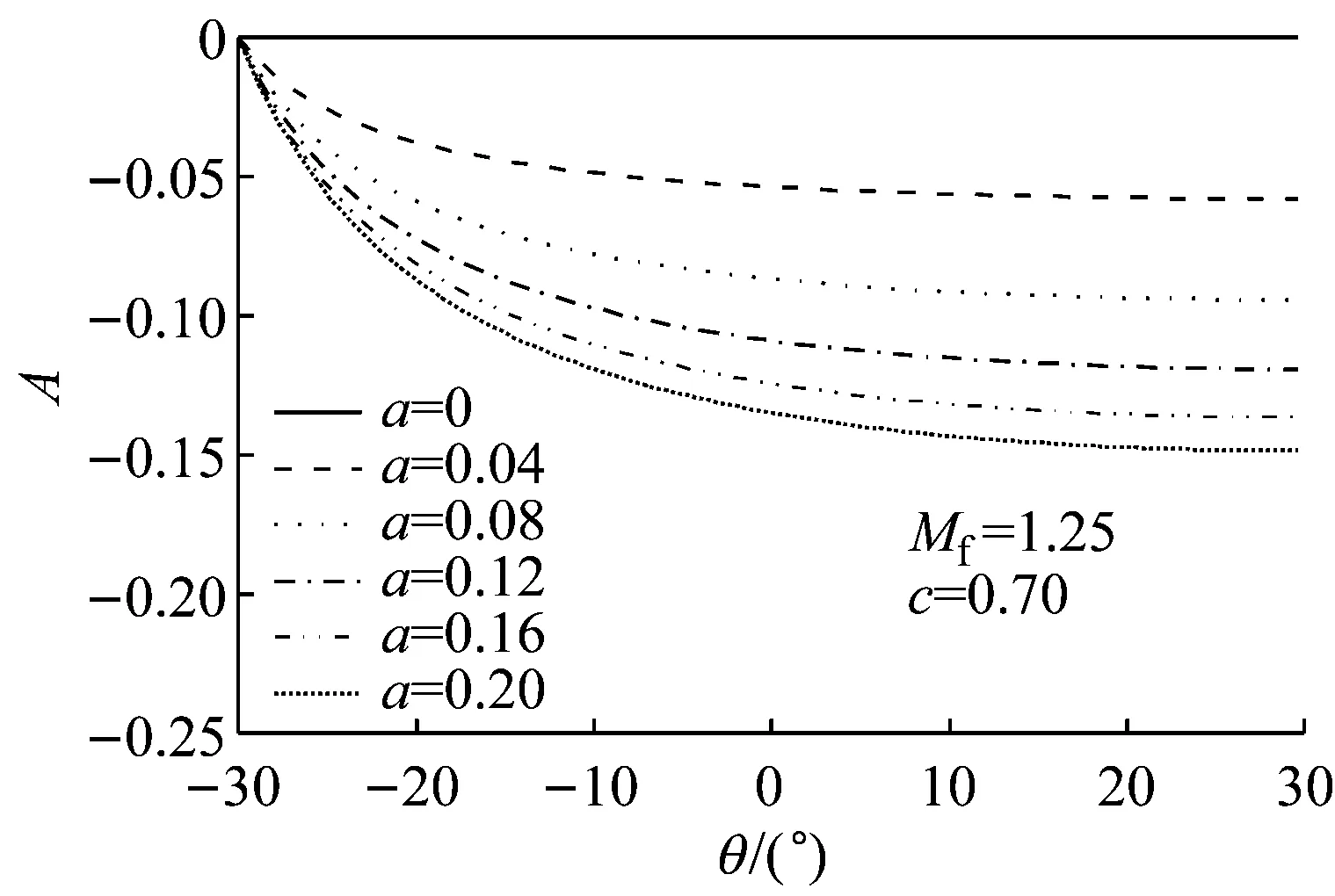
a 随各向异性程度变化规律

b 随中主应力系数的变化关系图1　各向异性状态变量与各向异性幅值的关系Fig.1　Anisotropic state variable vs anisotropic index

图1和图2表明基准点的选择对各向异性状态变量的影响较大.同时，基准点又是确定模型材料参数的试验点，试验点确定后，各向异性状态变量可以描述其他状态点对本构关系的影响.

本文定义的各向异性状态变量和现有状态变量[12,17-18]相比，具有以下特点：

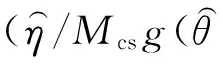
(2) 物理意义更清晰.本构关系一般采用常规三轴压缩试验来确定模型参数，试验土样不同程度存在各向异性，确定的模型参数已经包含了各向异性的影响，理论上常规三轴压缩确定的模型参数在这种应力状态下各向异性的影响应该不计.这也符合许多试验结果，如Ishihara[19]试验表明：常规三轴压缩试验条件下受原生各向异性影响较小，这与以上的理论分析一致；另外，Yang等[20]的试验结果也证明了这一点.

(3) 各向异性状态变量使用了基准点的思路，各向异性状态变量引入破坏准则后，在常规三轴压缩点自然符合试验结果.

(4) 模型建立中可以简化其描述形式.本构模型的材料状态、剪胀性以及硬化规律都与各向异性相关，定义的状态变量包含了较广的应力状态信息，这样可以简化本构关系，有助于砂土本构的描述.

a 随各向异性程度变化规律

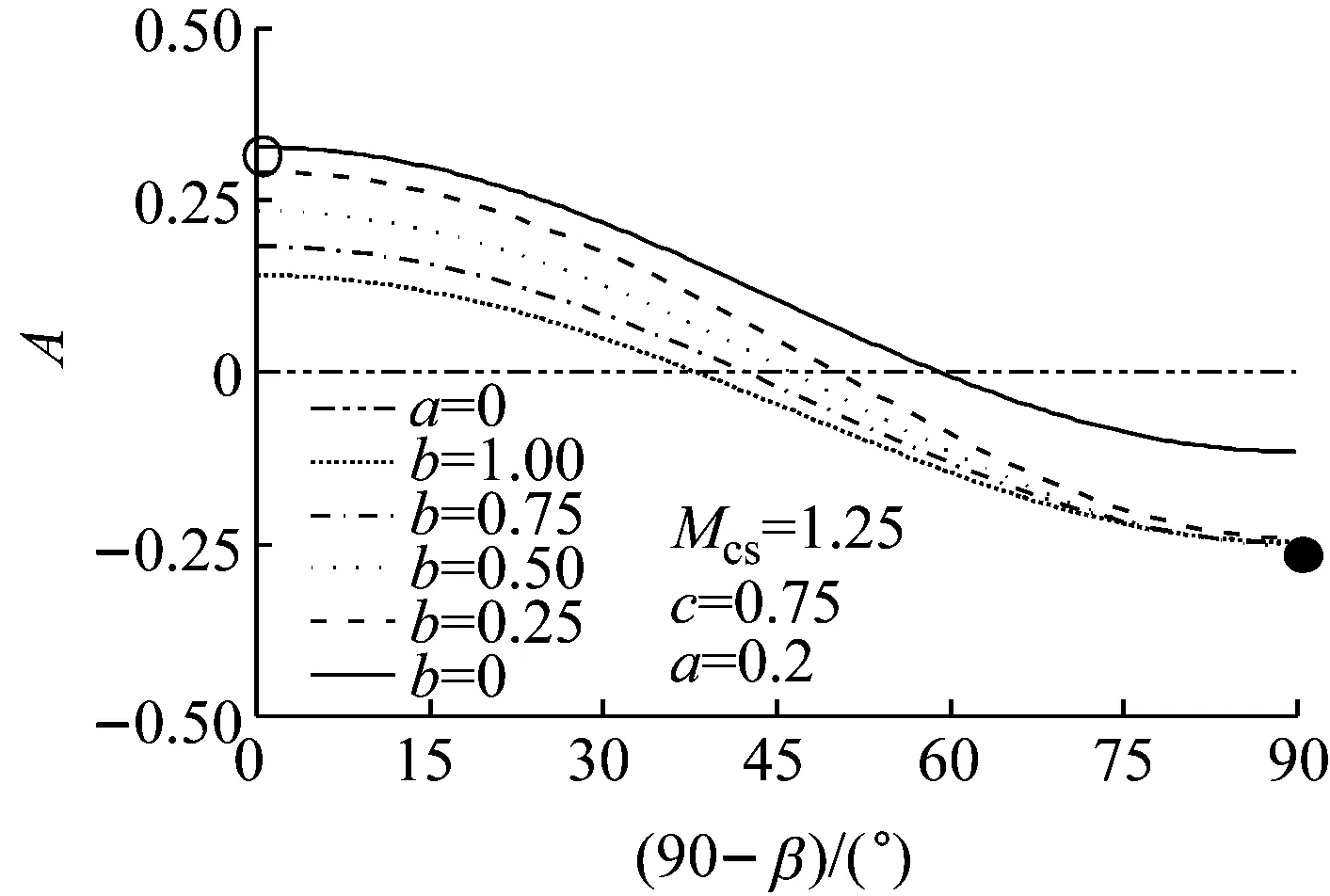
b 随中主应力系数的变化关系图2　各向异性状态变量与旋转角关系Fig.2　Anisotropic state variable vs rotation angle

1.3各向异性临界状态线的特点

越来越多砂土试验结果表明其临界状态线不惟一，其根本原因由于其各向异性的存在，各向异性的深层机理又可以归因其细观特性，因此砂土细观特性对其临界状态线有实质性影响.

根据Poulos等[21]认为砂土颗粒形状形成的各向异性主要对其临界状态线斜率影响较大，因此结合作者宏细观方面的工作[14]，参考Yang等[20]对临界状态线研究成果，将式(3)定义状态变量引入临界状态线得到

(4)

式中：eΓ，λc和ζ均为材料常数;p为平均有效应力；pa为大气压力；t为模型参数.t受三个因素(加载模式、各向异性和主应力相对组构旋转角)的影响.t通过常规三轴压缩和拉伸临界状态试验由式(4)得到.

2　模型框架

2.1屈服面

屈服面采用如下形式

(5)

式中：q为广义剪应力；M为硬化内变量；g(θσ)是θσ的函数，g(θσ)采用椭圆型[22]差值函数.

2.2硬化规律

硬化规则采用增量双曲线形式[23]，即

(6)

式中：G为弹性剪切模量；hs为模型参数，其取值可以用hs=(h1-h2e)得到，h1和h2为模型常数；Mp为峰值应力比，受状态参数的影响，其表达式为

(7)

式中：Ψ(A)为参考been等[24]状态参数的概念定义的状态参数，Ψ(A)=e-e(A);e为当前孔隙比;e(A)为式(4)定义的形式，kp是模型参数.从式(7)表达式可以看出Mp不是一个常数，是A的函数，与砂土细观组构相关.

2.3剪胀性

对于剪胀性，采用了Gajo和Muir Wood提出的方程[25]并考虑各向异性，将方程修正为

(8)

式中：d0为模型参数；Md为状态转换应力比，Md=Mcsg(θσ)e-kdΨ(A),Md不是一个常量，而是A的函数；kd为模型参数.当Ψ(A)>0时，砂土处于松散状态，加载时发生剪缩;当Ψ(A)<0时，砂土处于密实状态，加载产生剪胀现象.A由砂土组构张量定义，因此，Ψ(A)非常直观地将砂土细观特性和当前状态联系起来，将各向异性对剪胀的影响进行了量化.

综上所述，各向异性状态变量由砂土组构张量定义，将其引入本构模型之后，实际上将材料的细观特性和宏观方程联系起来.砂土细观参量变化时，临界状态线、硬化规律和剪胀方程也随之变化，模型采用宏细观结合的方法描述砂土的各向异性.

3　模型的验证与分析

3.1模型参数的确定

与各向同性模型相比，本文各向异性模型增加两个参数，即a和t.对于a，根据文献[20]取a=0.12.对于t，笔者等在文献[26]做了确定和大量三轴试验分析.根据文献[20]对Toyoura砂的试验，模型参数t由式(4)得到t=0.26，这样确定的参数对π平面上各向异性砂土的强度有较好描述，尤其是三轴压缩和三轴拉伸试验点.其他模型参数取值和文献[20]中Toyoura砂模型参数相同.

3.2模型参数验证

图3主要针对各向异性参量a和模型参数t两个参数进行验证.由于t是参考文献[20]宏细观结合的试验通过式(4)确定，也间接验证参数的符合性.本文选用不同沉积角度Toyoura砂的三轴试验结果对两个各向异性模型参数进行验证.试验的中主应力系数为0，与常规三轴压缩试验的加载方式一致.

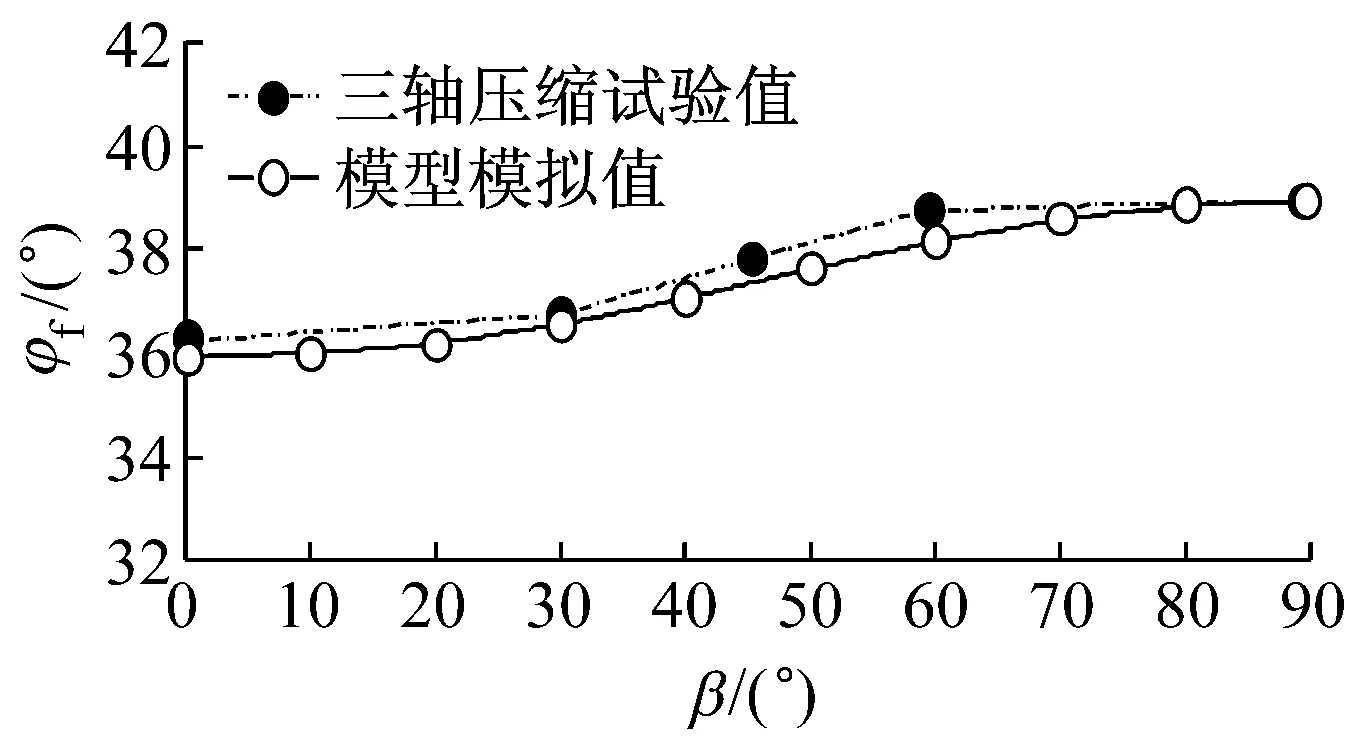
a 松砂

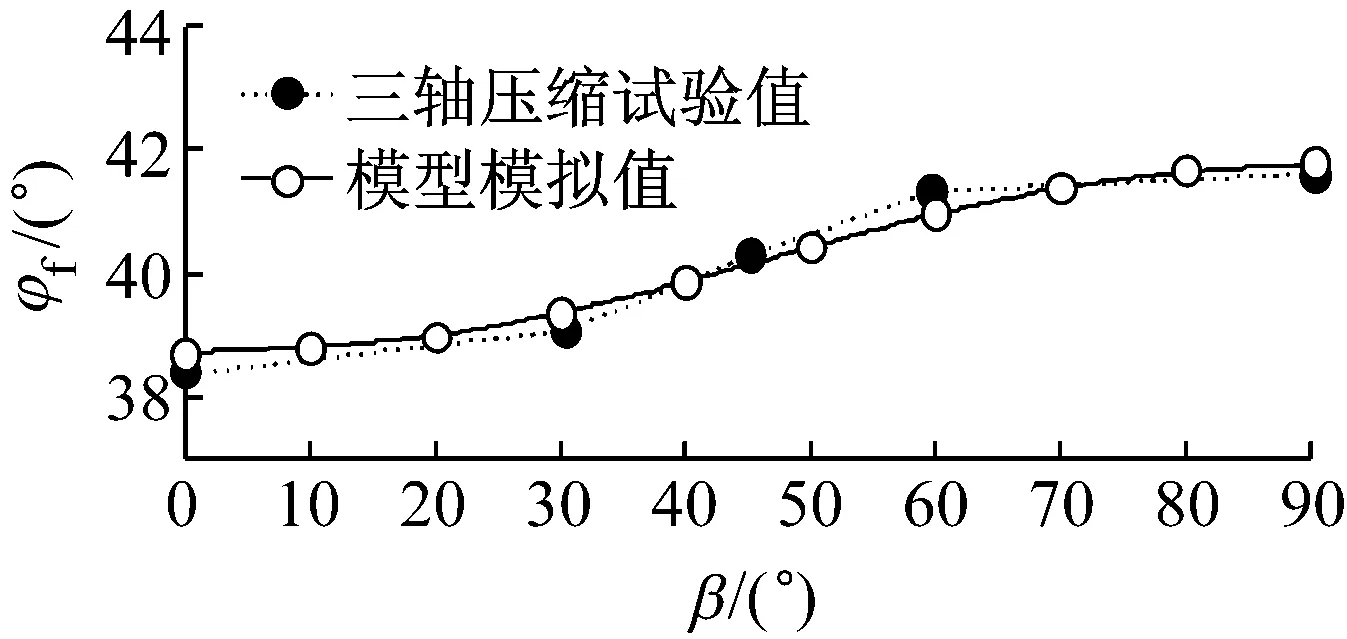
b 密砂图3　不同沉积角度Toyoura砂的三轴试验 强度关系(围压98 kPa)

Fig.3Strength relation of Toyoura sand with different angles of bedding plane to major stress in Triaxial test(at a confining pressure of 98 kPa)

图3中给出了Lam等[27]对Toyoura松砂和密砂的试验结果.试样采用不同沉积角度、同一围压下进行三轴压缩试验，松砂和密砂试验都得到随沉积角度的增加强度单调递增的规律.另外，Oda等[16]对Toyoura密砂和Abelev等[6]许多不同类型砂的真三轴试验也得到了相似的结论，因此图3中的规律具有一定普遍性.图3中的模拟可以看出确定的各向异性参数能够描述三轴条件下，同一围压、同一中主应力系数、不同沉积角度松砂和密砂的各向异性强度特性.

3.3各向异性对强度的影响

细观特性对强度的影响主要体现在π平面上.关于π平面上组构对强度影响的几何关系详见文献[14].图4为 Lam等[27]π平面上三个区间的试验结果及本文模拟.试验采用撒砂法制样，e=0.71，围压98 kPa，φf=42.5°.图4表明模型预测的峰值强度在三个区间表现出明显的各向异性，区间Ⅱ，Ⅲ相对区间Ⅰ的主要变化是大主应力轴相对沉积面旋转了90°，可见主应力方向变化对砂土峰值内摩擦角影响较大.总体上，各向异性强度曲线中心自然偏离了各向同性破坏曲线的中心(静水压力轴)，而且随着a的增大，破坏曲线的中心偏离越远，当a=0.12时在整个三个区内较好反映破坏强度；区间Ⅱ，Ⅲ要比区间Ⅰ的峰值内摩擦角小2°～5°，当 中主应力系数b=0和b=1时，模型预测和试验结果接近，各向异性细观参数能够反映Toyoura砂的原生各向异性对强度的影响.

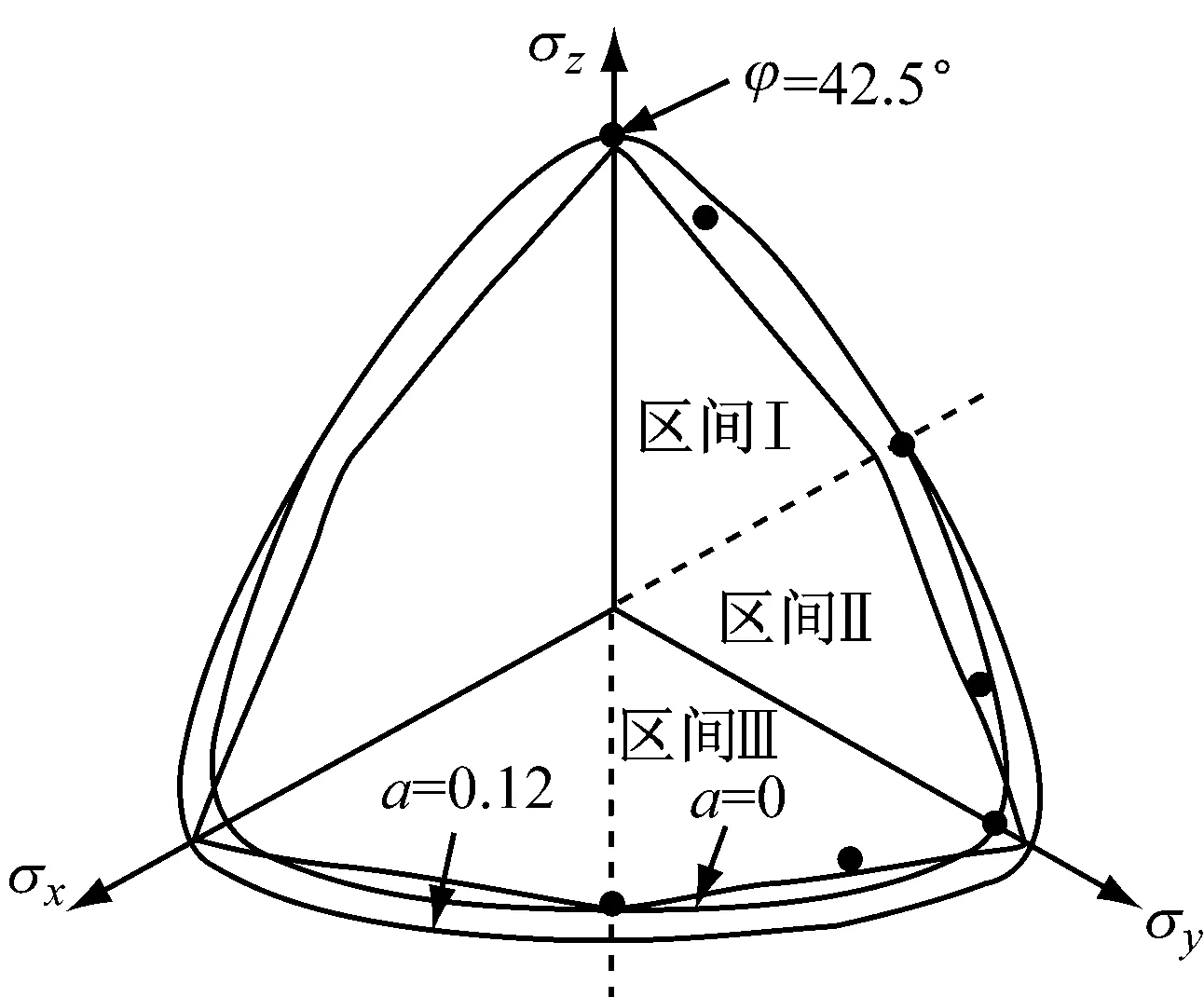
图4　各向异性Toyoura砂强度关系Fig.4　Strength relation of Toyoura sand

3.4三轴排水试验验证

三轴排水试验选用Oda[7,16]结合细观分析的试验结果.试验都选用Toyoura砂.Oda[16]采用两种颗粒含量的Toyoura砂进行试验，即Toyoura砂B和Toyoura砂D.其中B的细观颗粒含量主要以扁平颗粒为主，相对而言D则是球形颗粒含量较多，具体细观观测结果见文献[7].

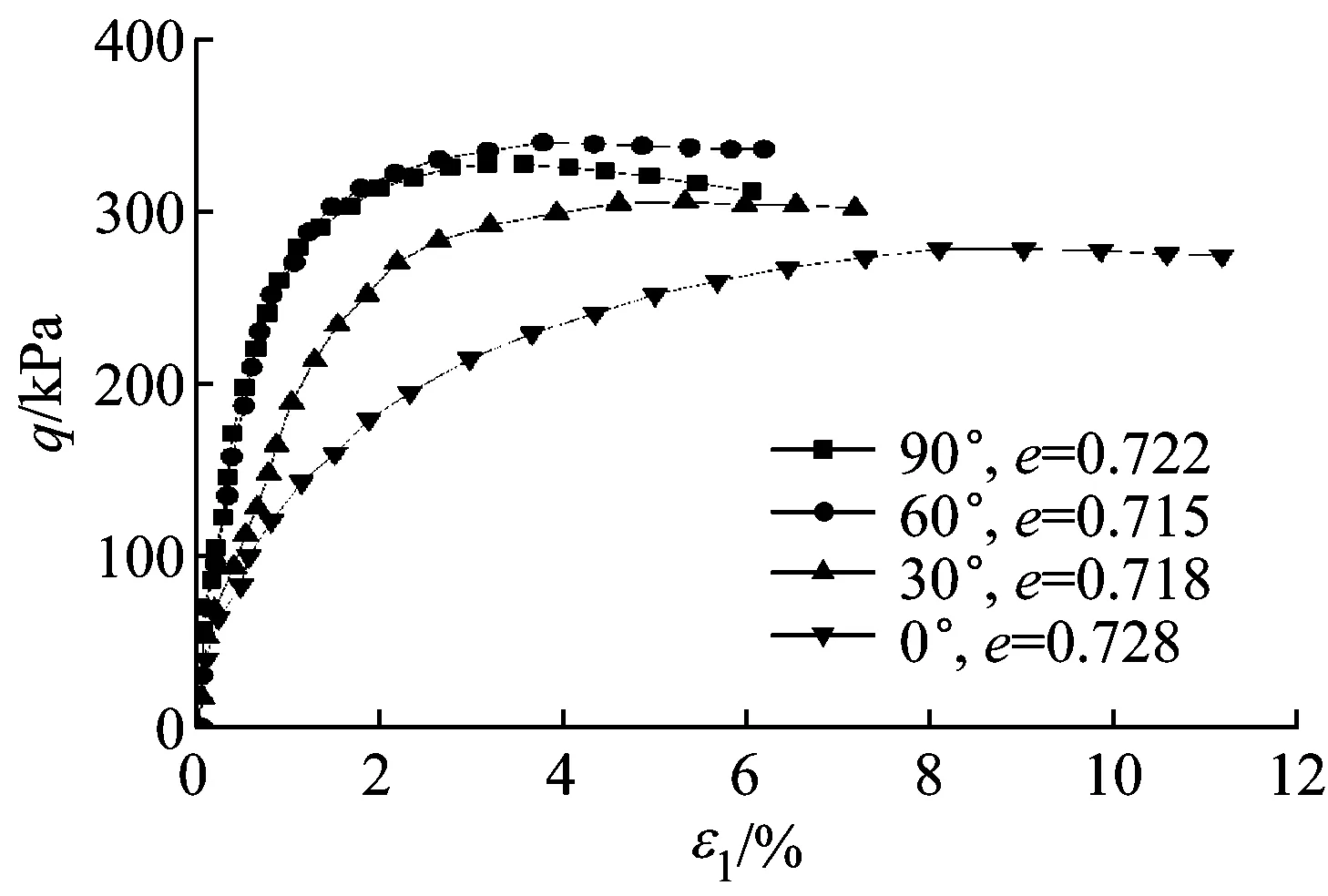
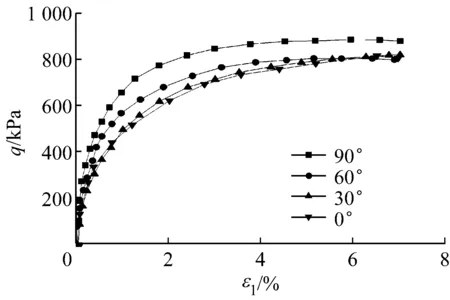
先对同一围压不同沉积角度的试验结果进行验证.选取两种围压和两种孔隙比的试验结果.图5为Oda[16]的试验结果，围压是98 kPa，孔隙比为e≈0.722，采用了90°，60°，30°和0°四种沉积角度的试样进行试验，图6为模型模拟.图7为Oda[7]的试验结果，围压是196 kPa，孔隙比为e=0.65～0.68，也采用了90°，60°，30°和0°四种沉积角度，图8为模型模拟；试验结果显示砂土的强度、剪胀特性和砂土颗粒的细观颗粒组成、颗粒形状、沉积方式的影响很大，其最大值和最小值相差50%左右.两个试验结果有一点不同之处是图5的试验强度和剪胀性随沉积面变化是60°时强度最大，而图7的试验结果则是随沉积面变化单调降低，目前关于Toyoura砂三轴排水试验规律多数是单调递减趋势.从图6和图8的模型模拟可见，各向异性模型能够较好描述随各向异性砂沉积面角度变化，强度和剪胀性单调减小的规律.

a 应力-应变

b 应变-体变图5　B型砂在围压98 kPa下的试验结果Fig.5　Results of sand B at a confining pressure of 98 kPa

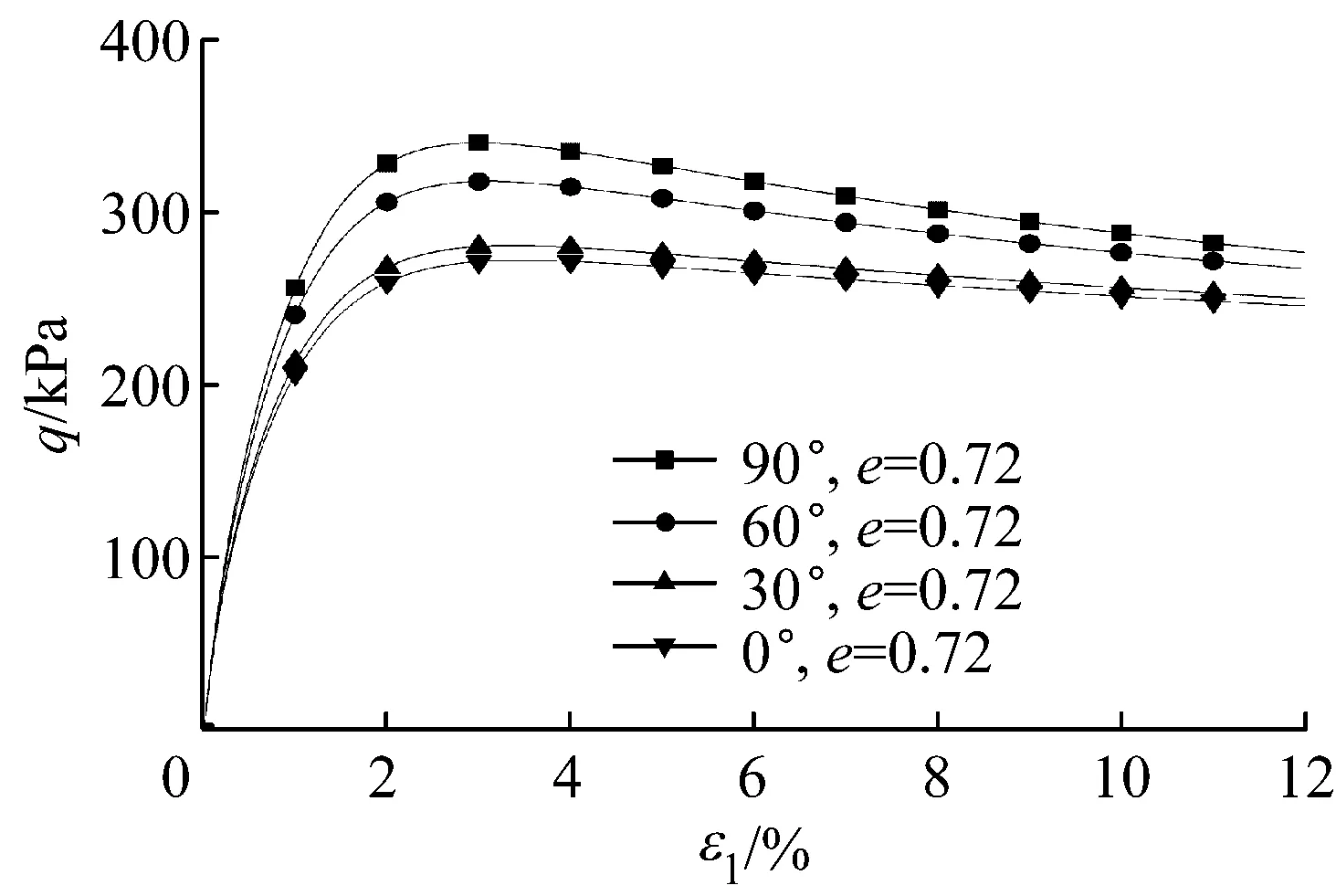
对同一沉积角度、同一围压不同孔隙比的试验验证.图9为Oda[16]的B型Toyoura砂试验结果，围压是98 kPa，沉积面角度固定为90°，采用三种孔隙比，即e=0.672，e=0.722和e=0.782.图10为本文的模拟结果，可以看出模型能够较好描述对同一围压和同一沉积角度试验所得到的强度和剪胀特性.

a 应力-应变

b 应变-体变图6　B型砂在围压98 kPa下的模拟Fig.6　Simulation of sand B at a confining pressure of 98 kPa

a 应力-应变

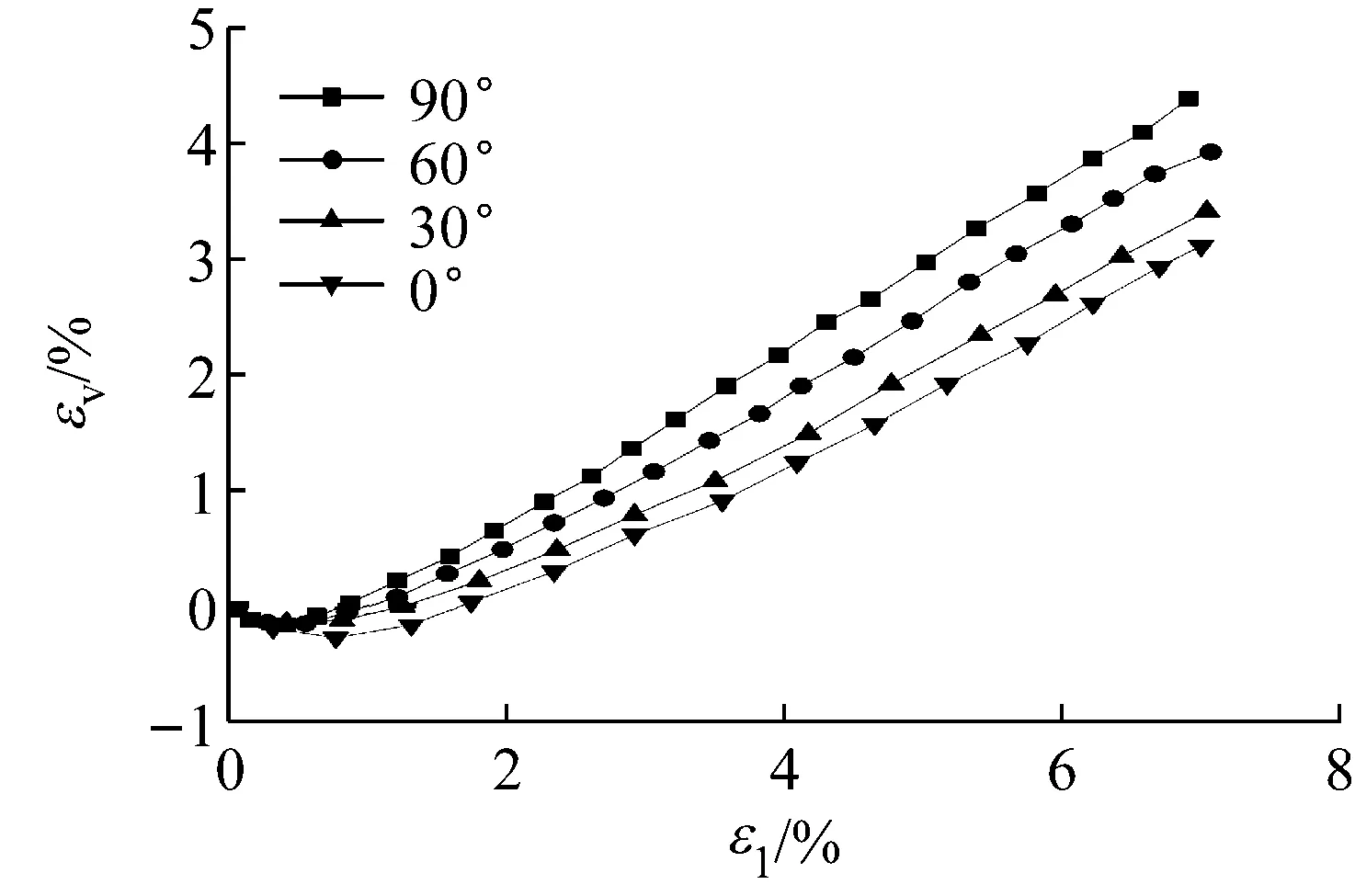
b 应变-体变图7　在围压196 kPa下的试验结果Fig.7　Results at a confining pressure of 196 kPa

综上所述，通过对多组各向异性Toyoura砂的排水三轴试验模拟验证，参考了砂土细观组构分析结果，本文模型使用一组参数能够较好描述在多种条件下砂土表现的各向异性强度和剪胀规律，充分说明了模型采用的描述各向异性方法的合理性.

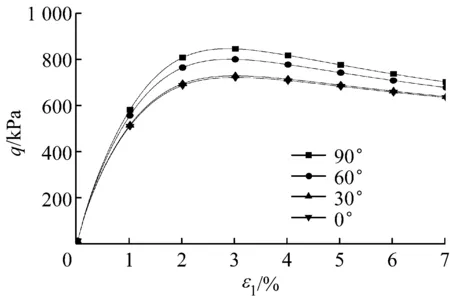
a 应力-应变

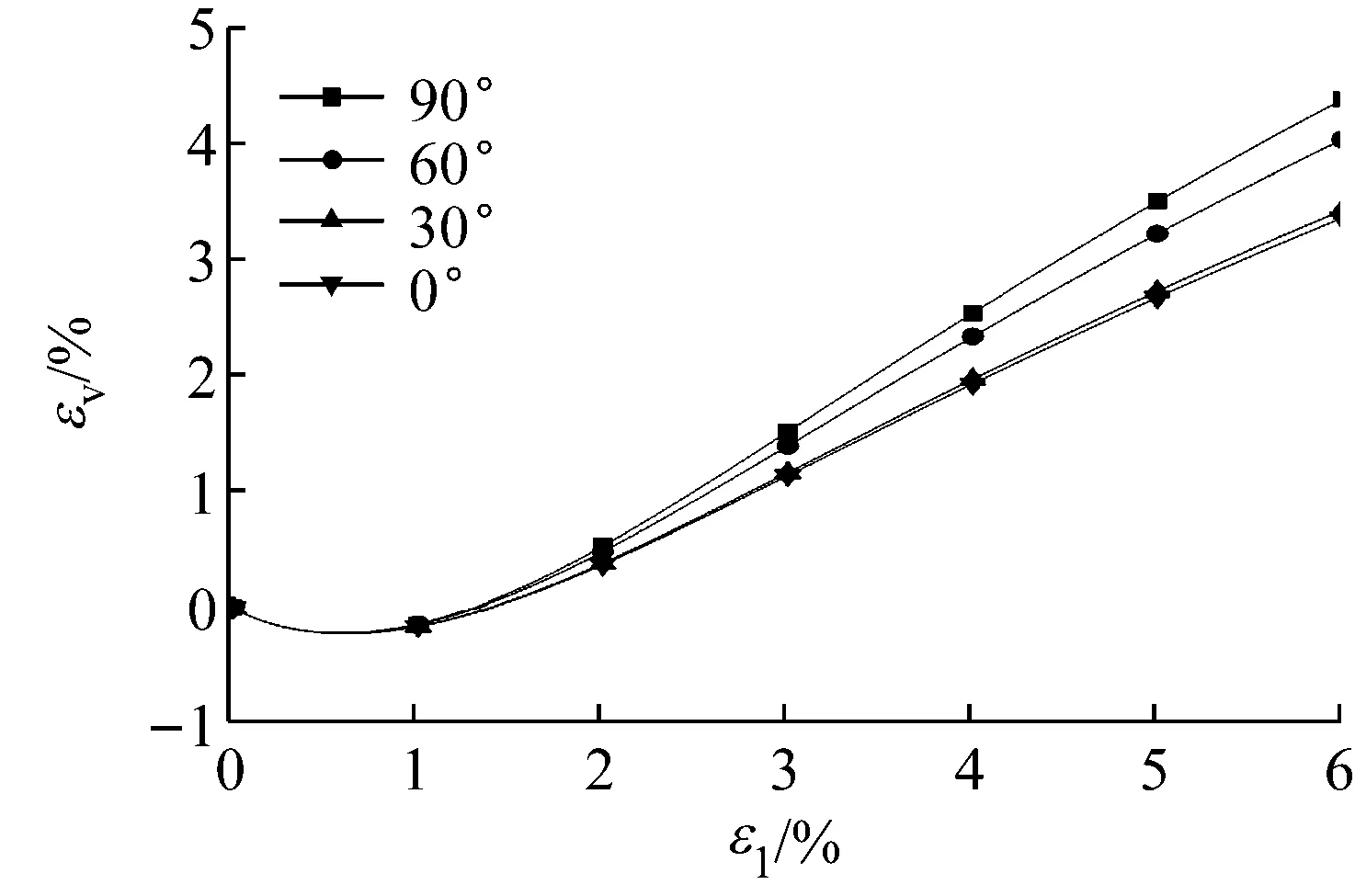
b 应变-体变图8　在围压196 kPa下的模拟Fig.8　Simulation at a confining pressure of 196 kPa

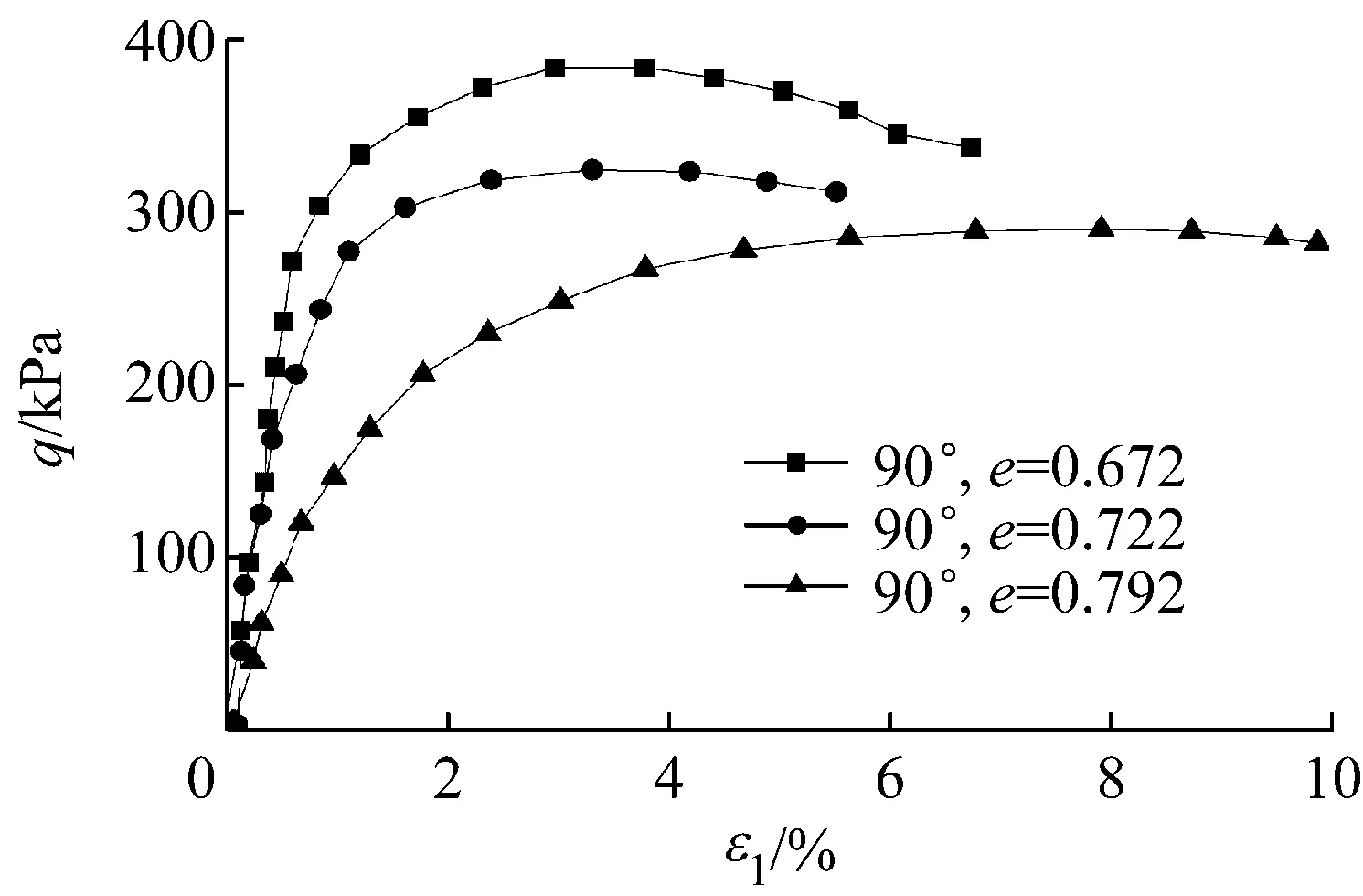
a 应力-应变

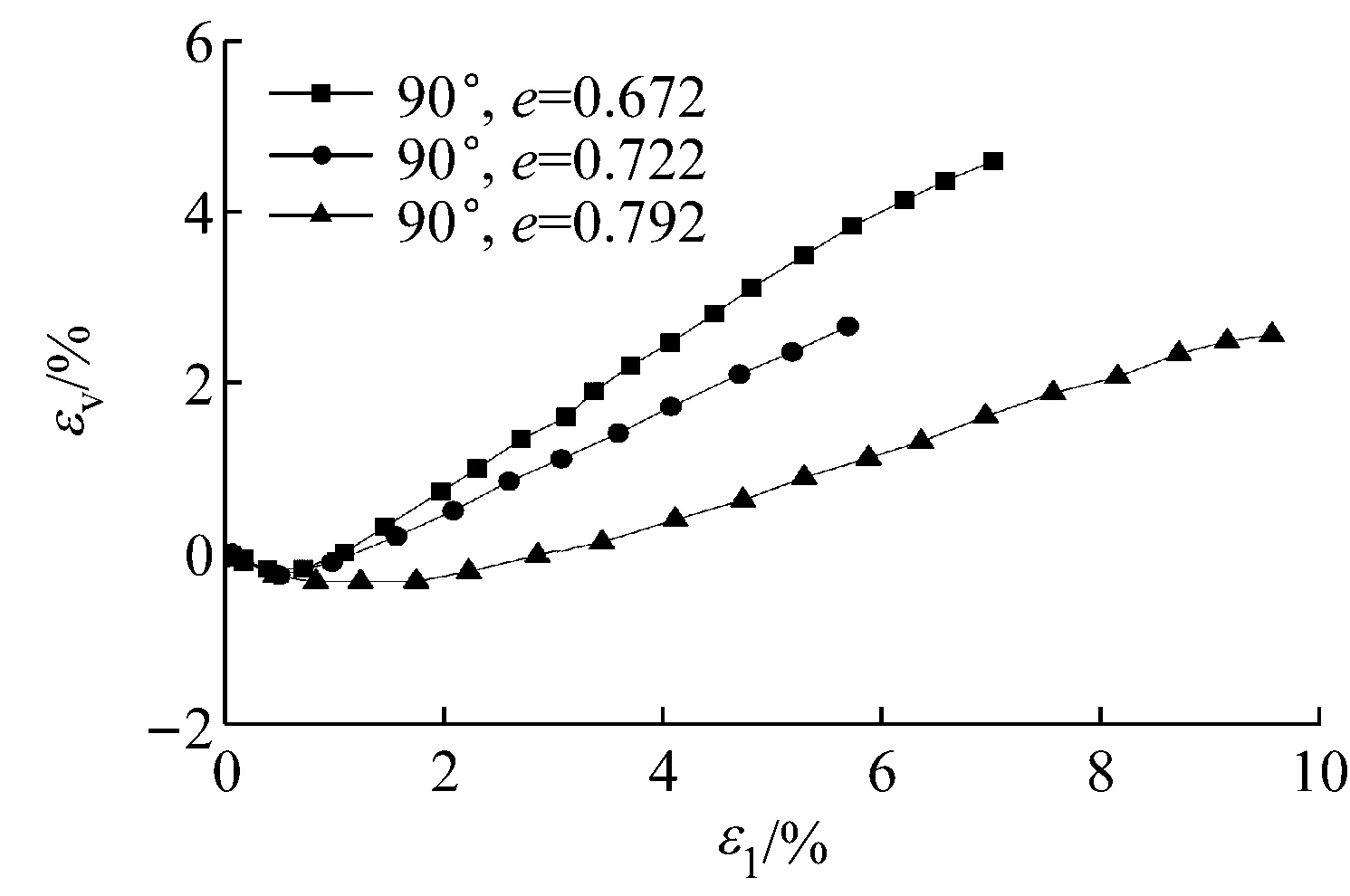
b 应变-体变图9　围压98 kPa相同沉积角度的试验结果

Fig.9Results at a confining pressure of 98 kPa with the same angle of bedding plane

4　结语

采用宏细观结合的方法建立本构模型对各向异性砂土的变形特性进行了模拟.该方法将新定义的各向异性状态变量引入本构模型来描述其宏观各向异性.各向异性状态变量引入模型后，临界状态线、硬化准则和剪胀方程都是各向异性状态变量、孔隙比和围压的函数，模型可以从细观角度解释更广的力学响应.

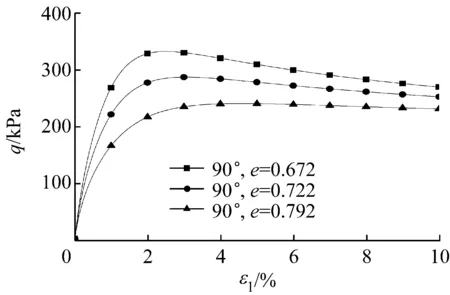
a 应力-应变

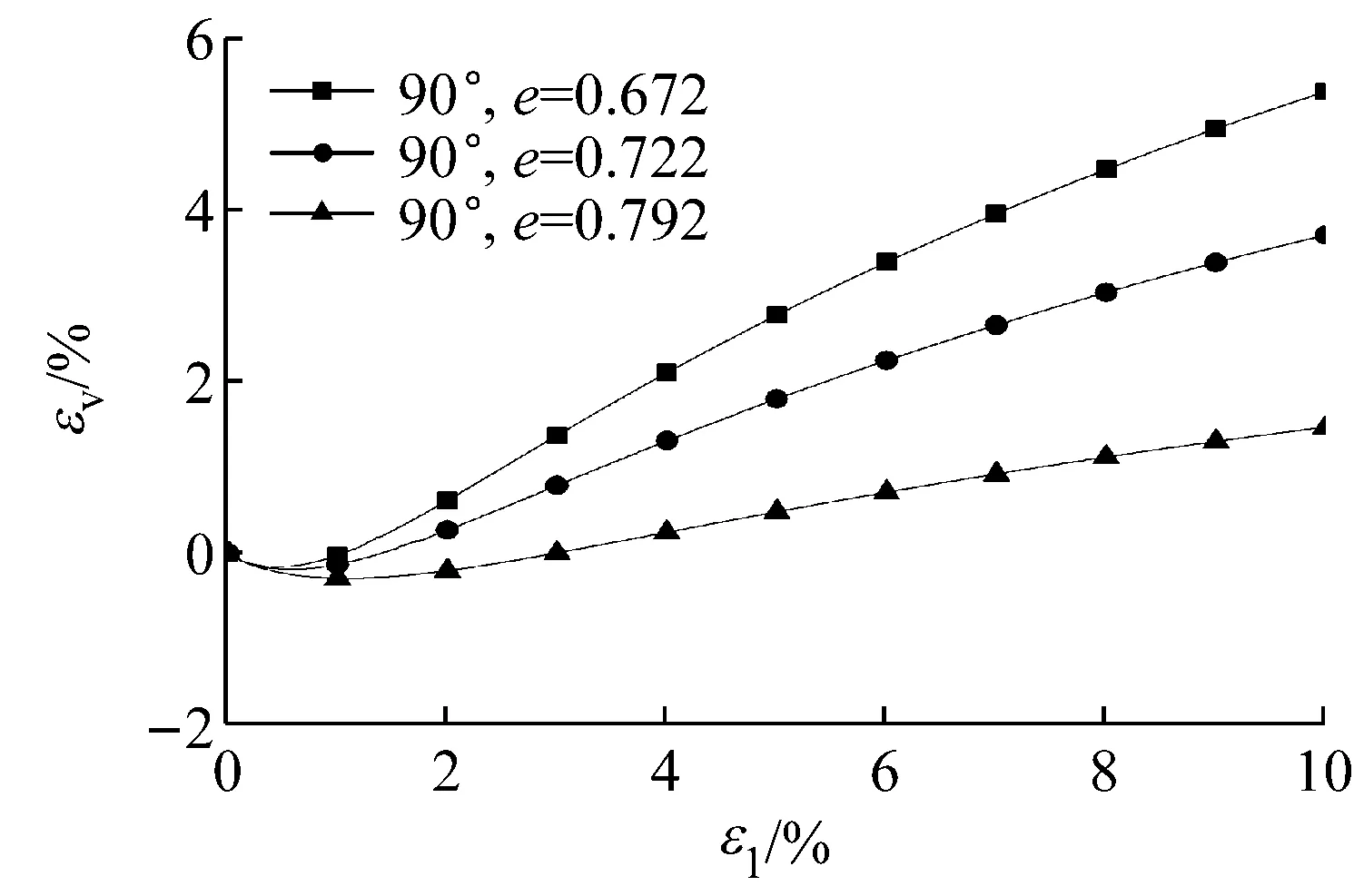
b 应变-体变图10　围压98 kPa相同沉积角度的模拟

Fig.10Simulation at a confining pressure of 98 kPa with the same angle of bedding plane

细观组构对砂土的临界状态线影响较大，它也是临界状态线不惟一的内在原因.通过各向异性状态参量，细观特性对临界状态线在π平面上的位置和形状影响较大.同时，当材料细观结构为各向异性时，各向异性状态变量随中主应力系数的变化而变化，因此，引入各向异性状态变量后，临界状态线将受细观组构、孔隙比、围压和加载模式的影响.利用Toyoura砂两种不同制样方法和细观结构的定量分析数据和三轴试验结果，初步验证了模型的有效性.

[1]CAI Zhengyin, LI Xiangsong. Deformation characteristics and critical state of sand[J].Chinese Journal of Geotechnical Engineering, 2004, 26 (5):697.

[2]Yao Y P, Kong Y X. Extended UH model: Three-dimensional unified hardening model for anisotropic clays[J]. Journal of Engineering Mechanics, 2012, 138(7): 853.

[3]黄茂松, 李学丰, 贾苍琴. 基于材料状态相关理论的砂土双屈服面模型[J].岩土工程学报, 2010, 31(11): 1764.

HUANG Maosong, LI Xuefeng, JIA Cangqin. A double yield surface constitutive model for sand based on state-dependent critical state theory[J]. Chinese Journal of Geotechnical Engineering, 2010, 31(11): 1764.

[4]Yamada Y, Ishihara K. Anisotropic deformation characteristics of sand under three-dimensional stress conditions[J]. Soils and Foundations, 1979, 19(2): 79.

[5]Arthur J R F, Menzies B K. Inherent anisotropy in a sand[J]. Geotechnique, 1972, 22(1): 115.

[6]Abelev A V, Lade P V. Effects of cross-anisotropy on three-dimensional behavior of sand I: Stress-strain behavior and shear banding[J]. Journal of Engineering Mechanics: ASCE, 2003, 129(2): 160.

[7]Oda M. Experimental study of anisotropic shear strength of sand by plane strain tests[J]. Soils and Foundations, 1978, 18(1): 25.

[8]Ohta H. Analysis of deformation of soils based on the theory of plasticity and its application to settlement of embankment[D]. Kyoto: Kyoto University, 1971.

[9]Dafalias Y F. Anisotropic critical state soil plasticity model[J]. Mechanics Research Communications, 1987, 13(6): 341.

[10]Rouainia M, Muir W D. A kinematic hardening constitutive model for natural clays with loss of structure[J]. Geotechnique, 2000, 50(2): 153.

[11]Houlsby G T, Sharma R S. A conceptual model for the yielding and consolidation of clays[J]. Geotechnique, 1999, 49(4): 491.

[12]Li X S, Dafalias Y F. Constitutive modelling of inherently anisotropic sand behavior[J]. Journal of Geotechnical and Geoemvironmental Engineering: ASCE, 2002, 128(10): 868.

[13]Pietruszczak S, Mroz Z. Formulation of anisotropic failure criteria incorporating a microstructure tensor[J]. Computers and Geotechnics, 2000, 26, 105.

[14]李学丰, 黄茂松, 钱建固. 宏细观结合的砂土各向异性破坏准则[J]. 岩石力学与工程学报, 2010, 29(9): 1885.

LI Xuefeng, HUANG Maosong, QIAN Jiangu. Failure criterion of anisotropic sand with the method of macro-micro incorporation[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(9): 1885.

[15]Oda M. Initial fabrics and their relations to mechanical properties of granular materials[J]. Soils and Foundations, 1972, 12(1): 17.

[16]Oda M. The mechanism of fabric changes during compressional deformation of sand[J]. Soils and Foundations, 1972, 12(2): 1.

[17]Wan R G, Guo P J. Effect of microstructure on undrained behaviour of sands[J]. Canadian Geotechnical Journal, 2001, 38(1): 16.

[18]Dafalias Y F, Papadimitriou A G, Li X S. Sand plasticity model accounting for inherent fabric anisotropy[J]. Journal of Engineering Mechanics, 2004, 130(11):1319.

[19]Ishihara K. Liquefaction and flow failure during earthquakes[J]. Geotechnique, 1993, 43(3): 351.

[20]Yang Z X, LI X S, Yang J. Quantifying and modelling fabric anisotropy of granular soils[J]. Geotechnique, 2008, 58(4): 237.

[21]Poulos S J, Castro G, France J W. Liquefaction evaluation procedure[J]. J Geotech Eng, 1985, 111(6): 772.

[22]William K J, Warnke E P. Constitutive model for the triaxial behavior of concrete[C]∥International association for bridge and structure engineering proceedings. Bergamo:[s.n.],1975:117-131.

[23]Li X S, Dafalias Y F. Dilatancy for cohesionless soils[J]. Geotechnique, 2000, 50(4): 449.

[24]Been K, Jefferies M G. A state parameter for sands[J]. Geotechnique, 1985, 35(2): 99.

[25]Gajo A, Muir-Wood D. A kinematic hardening constitutive model for sands: The multiaxial formulation[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1999, 23(9): 925.

[26]黄茂松, 李学丰, 钱建固. 各向异性砂土的应变局部化分析[J].岩土工程学报, 2012, 34(10): 1885.

HUANG Maosong, LI Xuefeng, QIAN Jiangu. On strain localization of anisotropic sands[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(10):1885.

[27]Lam W K, Tatsuoka M. Effect of initial anisotropic fabric andσ2on strength and deformation characteristics of sand[J]. Soils and Foundations, 1988, 28(1): 89.

Deformation Analysis of Anisotropic Sand Using the Method of Macro-meso Incorporation

LI Xuefeng1, KONG Liang2, YUAN Qi1, WANG Yanchang1

(1. School of Physics Electrical Engineering, Ningxia University, Yinchuan 750021, China; 2. School of Sciences, Qingdao Technological University, Qingdao 266033, China)

The deformation analysis of anisotropic sand was conducted by employing the constitutive model with the method of macro-meso incorporation. A novel anisotropy state variable which is properly defined in the term of fabric tensor was imployed and a constitutive model for anisotropic sand was proposed with incorporation of the novel anisotropy state into the critical state line(CSL). After the introduction of the novel anisotropy state, the critical state surface and other state surfaces of the model offset from the axes of hydrostatic pressure for the degree of anisotropy. The CSL, the harding rule and the dilatancy equation of model are the function of void ratio, confining pressure, shear-mode and anisotropy variable. One set of model constants can simulate well the strength-deformation responses of sand under different confining pressures and different densities. The simulation of strength experimental data and the simulation of the deformation results for Toyoura sand contained analysis of microstructure verify the proposed method can be validated from the verification.

sand; macro-meso; strength; anisotropy

2015-01-28

国家自然科学基金(51368050,11572165)；宁夏自然科学基金重点项目(NZ13001)；宁夏科技支撑计划(2013年)

李学丰(1976—)，男， 副教授, 工学博士，主要研究方向为环境岩土工程及岩土本构理论.E-mail:lixuefeng1928@163.com

TU443

A