盾构隧道管片接头的易损性分析和评价

黄宏伟， 沈贤达， 王　飞， 张东明

(1. 同济大学 土木工程学院， 上海 200092； 2. 同济大学 岩土及地下工程教育部重点实验室， 上海 200092；3. 上海防灾救灾研究所， 上海 200092)



盾构隧道管片接头的易损性分析和评价

黄宏伟1,2， 沈贤达1,2， 王飞3， 张东明1,2

(1. 同济大学 土木工程学院， 上海 200092； 2. 同济大学 岩土及地下工程教育部重点实验室， 上海 200092；3. 上海防灾救灾研究所， 上海 200092)

管片接头是盾构隧道结构力学性能的薄弱和关键部位.从抗弯、抗剪及抗渗三个方面，提出接头易损性评价方法.在轴力、弯矩和剪力作用下，考虑接头自身健康状况，并以混凝土、螺栓的应力状况和渗漏水作为评价指标，建立接头易损性评价模型.建立管片接头力学解析模型，分析接头的力学响应，并建立管片接头三维有限元精细化模型，对比验证解析模型的正确性.通过蒙特卡洛计算，获得大量计算样本，并在此基础上构建管片接头易损性的贝叶斯网络.根据接头易损性贝叶斯网络，分析接头易损性，并结合现场监测，反分析盾构隧道管片接头的健康状况，更新接头易损性预测，指导盾构隧道的正常运营维护.

盾构隧道； 管片接头； 易损性分析； 贝叶斯网络

盾构隧道结构的主要病害如过大的收敛变形、纵向不均匀沉降、渗漏水和裂缝等，在很大程度上与管片接头变形和损坏有关.接头是盾构隧道结构薄弱且较敏感的部位.无论从整环衬砌结构受力安全还是接头局部承载与防水使用安全出发，对接头的分析研究都是必不可少的关键环节.Lee K M等[1]和张冬梅等[2]认为接头的刚度是影响盾构隧道结构径向变形的关键因素.合理、有效、方便地评价接头的健康状况，有助于隧道整体结构的健康评估.

针对盾构隧道管片接头，已有较多的相关研究.林光俊[3]进行了东京一共同沟工程的管片接头实体试验的加载试验.Zhang Wenjun等[4]、郭瑞等[5]和赵明等[6]分别针对接头的抗弯、抗剪、抗渗性能，做了模型试验，得到在轴力、弯矩、剪力下，接头抗弯、抗剪的力学规律和接头渗漏水机理.李剑[7]通过对运营隧道的现场健康状况检测，考虑隧道结构耐久性，评价隧道结构性能.目前，针对接头的研究主要是对各影响因素单独进行确定性分析，未能综合考虑各个影响因素及其不确定性.然而，盾构隧道所处的地质环境存在较大的变异性，由于施工和运营环境的影响，结构自身的健康状况也存在不确定性.因此，提出一种能综合考虑外界扰动和接头自身的健康状况，并考虑不确定性的评价方法，有很强的现实意义.

易损性分析作为一种能综合考虑各影响因素及其不确定性的方法，能合理、有效地评估事物的状态，找到薄弱环节，为未来的决策和安全措施提供依据.近几年，易损性分析已逐渐在土木工程领域中引起重视.黄栩等[8]通过分析灾害强度I与承险体自身抵抗能力R的函数，评价上部基坑开挖对盾构隧道易损性的影响.于刚等[9]采用损伤场景对结构性能的影响程度(CI)和损伤场景占结构体系总体规模的比例(MI)两个参数进行桥梁易损性分析评价.Saeidi等[10]根据易损性曲线分析隧道开挖对上部建筑物的影响.然而，现有研究方法虽能简单评价结构易损性，但未综合考虑各因素的不确定性，且无法根据结构当前状况，推测其他病害发生的概率并反分析结果自身健康状况，指导结构的运营维护.

而贝叶斯网络可将概率统计应用于复杂领域，能综合考虑各影响因素的关系，是进行不确定性推理和反分析的有效工具.贝叶斯网络能科学预测结构的易损性等级，并依据监测数据，反分析结构的受力和健康状况.Sousa等[11]、周健等[12]已将贝叶斯网络运用到隧道施工的风险评价中，但至今没有学者通过贝叶斯网络评价盾构隧道运营阶段的易损性.因此，结合盾构隧道接头受力特点，本文提出基于贝叶斯网络的盾构隧道接头易损性评价方法，评价接头的安全性能，分析接头的薄弱环节.

本文先构建接头易损性贝叶斯网络结构，再通过接头模型解析求解，分析接头完成力学、防水等目标的条件概率，以此建立盾构隧道接头贝叶斯网络模型，从而研究接头易损性，找到接头损伤的关键部位.根据现场监测结果，通过贝叶斯网络的反分析功能，分析最有可能的致病因素，从根源上处理病害，指导隧道的加固和修护.

1　管片接头易损性模型的构建

结构的易损性(vulnerability)是指结构容易受到伤害或者损伤的程度，在一定强度的意外荷载作用下结构发生失效的概率[13].易损性的概念起源于控制工程，然后逐渐运用于电力系统、人类和社会学系统、金融系统、生命线工程.与此同时，随着工程师对结构易损性认知水平的提高，结构易损性的研究逐渐得到重视，现在易损性已成为工程风险分析中最基本的元素之一.结构易损性分析可整体评价结构的安全性能，对加强局部危险点，提高结构整体安全性能有较强的指导作用.

易损性模型的构建应先明确致险因子和易损性评价指标，然后建立致险因子与易损性评价指标之间的关系.本文以接头所受的弯矩、轴力和剪力为致险因子，考虑接头健康状况，以螺栓、混凝土的应力及渗漏水为评价指标，建立接头易损性评价模型.

在设计规定服役期限内，盾构隧道结构随着运营时间的增长，由于环境、受力等因素，结构的健康状况会下降，安全性和耐久性能逐渐衰减.隧道衬砌外侧一般承受较大的水土压力作用，受到水、土环境直接影响，非常可能发生渗透问题.同时水土中的氯离子、硫酸盐等有害物质将随水体迁移，可能接触并腐蚀衬砌结构.而隧道结构内侧一般直接与空气接触，主要受空气中的水蒸气、CO2和SO2等有害气体的影响.接头连接螺栓与空气直接接触，且渗漏水会锈蚀螺栓，接头螺栓的健康状况也会随服役时间的增加而恶化.因此，混凝土因碳化、氯离子腐蚀以及管片拼装受损导致承载能力下降，钢筋和螺栓因锈蚀导致有效截面减小，混凝土和螺栓性能下降均会影响接头的工作性能[8].

除了接头自身的健康状况，接头的受力状况对其易损性的影响也很大.在弯矩的作用下，接头张开量随弯矩的增加逐渐变大.当弯矩过大，接头处混凝土可能会被局部压溃，接头螺栓受拉屈服.此时，接头抗弯刚度迅速减小，接头产生较大的张开量.本文以接头混凝土和螺栓的应力作为易损性指标，结合接头自身的健康状况(混凝土强度折减系数和螺栓截面锈蚀率)，分析在轴力和弯矩作用下，接头的抗弯易损性.

混凝土应力的安全等级可由使混凝土材料达到屈服和破坏状态的应力确定.本文采用的管片混凝土强度等级为C55，混凝土本构模型参考张厚美等提出的Saenz三折线简化模型[14].如图1所示.图中：σa为直线段a点的应力；σb为(b点)临界应力，σb=0.75σc；σc为塑性变形段(bc)的最大应力，取混凝土轴心抗压强度,σc=35.5 MPa.取εc=0.002.将模型分为三段折线Obcd′，其中取cd′段为水平直线.根据混凝土材料的临界应力和最大应力，混凝土应力安全状况等级如表1所示.

螺栓拉应力的安全等级可由使螺栓达到屈服和破坏状态的应力确定.本文采用的螺栓强度为5.8级，假定螺栓受拉的应力-应变关系为弹塑性，如图2所示.

图1　混凝土应力-应变曲线Fig.1　Stress-strain curve of concrete表1　接头混凝土应力安全等级表Tab.1　Safty scales of joint concrete stress

接头混凝土应力/MPa安全等级0～26.625C1:混凝土应力尚未达到屈服临界点,接头刚度较大,接头混凝土处于健康状态.>26.625～35.500C2:混凝土应力超过屈服临界点,刚度逐渐降低,接头混凝土处于警戒状态.>35.500C3:局部混凝土压溃,接头混凝土处于危险状态.

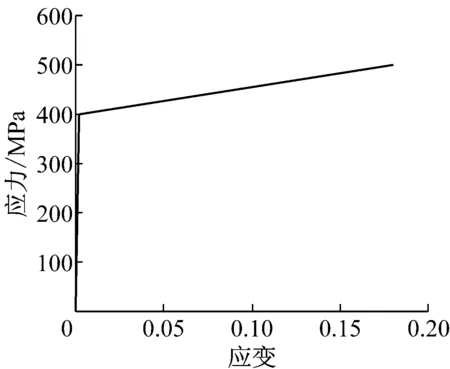
图2　螺栓应力-应变曲线Fig.2　Stress-strain curve of bolt

螺栓屈服拉应变取0.002，弹性模量取Eb=2.0×105MPa.根据螺栓的屈服应力，螺栓的应力安全状况等级如表2所示.

表2　螺栓拉应力安全等级表Tab.2　Safty scales of tensile stress in bolt

在剪力的作用下，混凝土之间的摩擦力不足以抵抗接头所受的剪力时，接头会产生相对滑移，形成错台.此时，螺栓承担大部分剪力作用，并可能受剪破坏.结合接头自身的健康状况，本文研究在轴力和剪力作用下，接头的抗剪易损性.根据螺栓是否受剪或受剪破坏，接头剪应力安全状况等级如表3所示.

表3　螺栓剪应力安全等级表Tab.3　Safty scales of shear stress in bolt

弹性密封垫的工作状态对接头的防水性能影响非常大.由于弯矩和剪力的作用，弹性密封垫可能会因接触面所受压力不足以及接触面积下降导致防水性能下降[6]，当接头张开量大于6 mm，或者管片间错动大于8 mm时[15]，接头抗渗性能受到较大影响，本文以此为接头渗漏水易损性评价指标.

2　接头易损性分析

2.1多因素影响的贝叶斯网络模型

本文采用贝叶斯网络分析接头易损性.贝叶斯网络是一个带有条件概率表的有向无环图.网络的每个节点代表一个变量，节点之间的有向连接表示变量之间的条件依赖关系.其中，节点A指向的所有节点为节点A的子节点，节点A被称为其所有子节点的父节点.贝叶斯网络以贝叶斯公式为基础，通过有向无环图定性地描述了变量之间的依赖和独立关系，并用条件概率定量地描述了变量对其父节点的依赖关系.因此，要构建完整的贝叶斯网络需分两步，即构建贝叶斯网络结构和学习条件概率表.

贝叶斯公式：设事件D的样本空间S，A为D的基本事件，基本事件B1，B2，B3,…，Bn互不相容，B1∪B2∪B3∪…∪Bn=S,1≥P(A)≥0，1≥P(Bi)≥0，i=1,2，…，n，则由乘法法则与条件概率公式有

(1)

式(1)为贝叶斯网络在数据分析与概率推理时应用的贝叶斯公式，运用基本事件的先验概率来推导事件的后验概率.式中P(Bi)表示事件Bi发生的先验概率,P(Bt|A)表示在事件A发生的条件下事件Bt发生的后验概率.

运用贝叶斯网络进行盾构隧道接头易损性分析，需要构造所描述问题的网络结构.由接头易损性模型可知，外力和接头自身健康状况都会对接头抗弯、抗剪、抗渗性能造成影响.因此，本文着重研究不同健康状况的接头受到轴力、剪力和弯矩复合作用时，接头的力学响应.以混凝土应力、螺栓拉应力、螺栓剪应力和接头抗渗漏水性能作为指标评价接头易损性，构建贝叶斯网络结构，如图3所示.

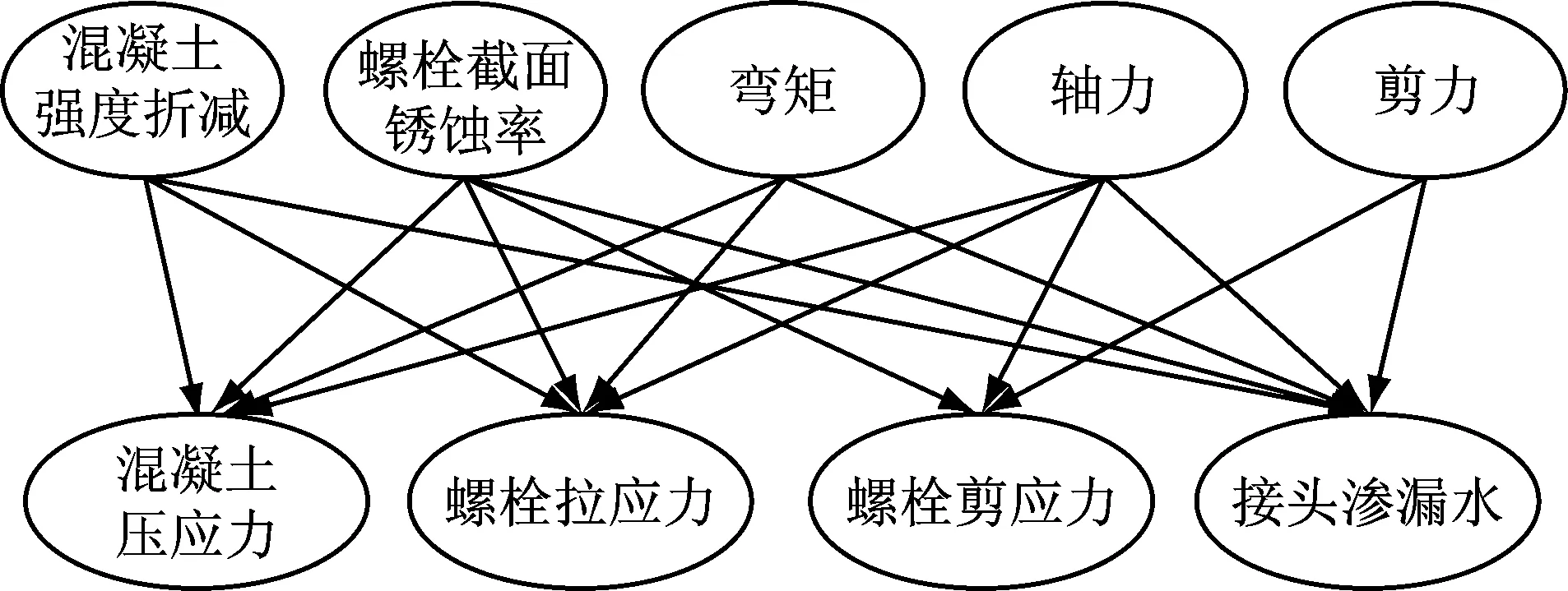
图3　接头易损性的贝叶斯网络结构图Fig.3　Bayesian network structure of vulnerbility of joints

2.2接头模型参数

确定贝叶斯网络结构后，需分析各相关变量之间的依赖关系，通过参数学习，获得条件概率表.本文采用解析计算的方法建立贝叶斯网络学习案例集，并计算各个指标的条件概率.力学解析模型包括接头抗弯力学模型和接头抗剪力学模型.本文基于上海典型盾构隧道环向接头构建分析模型，并作了一定的简化.具体构造形式如图4所示，管片为混凝土直接接触，不设传力衬垫.

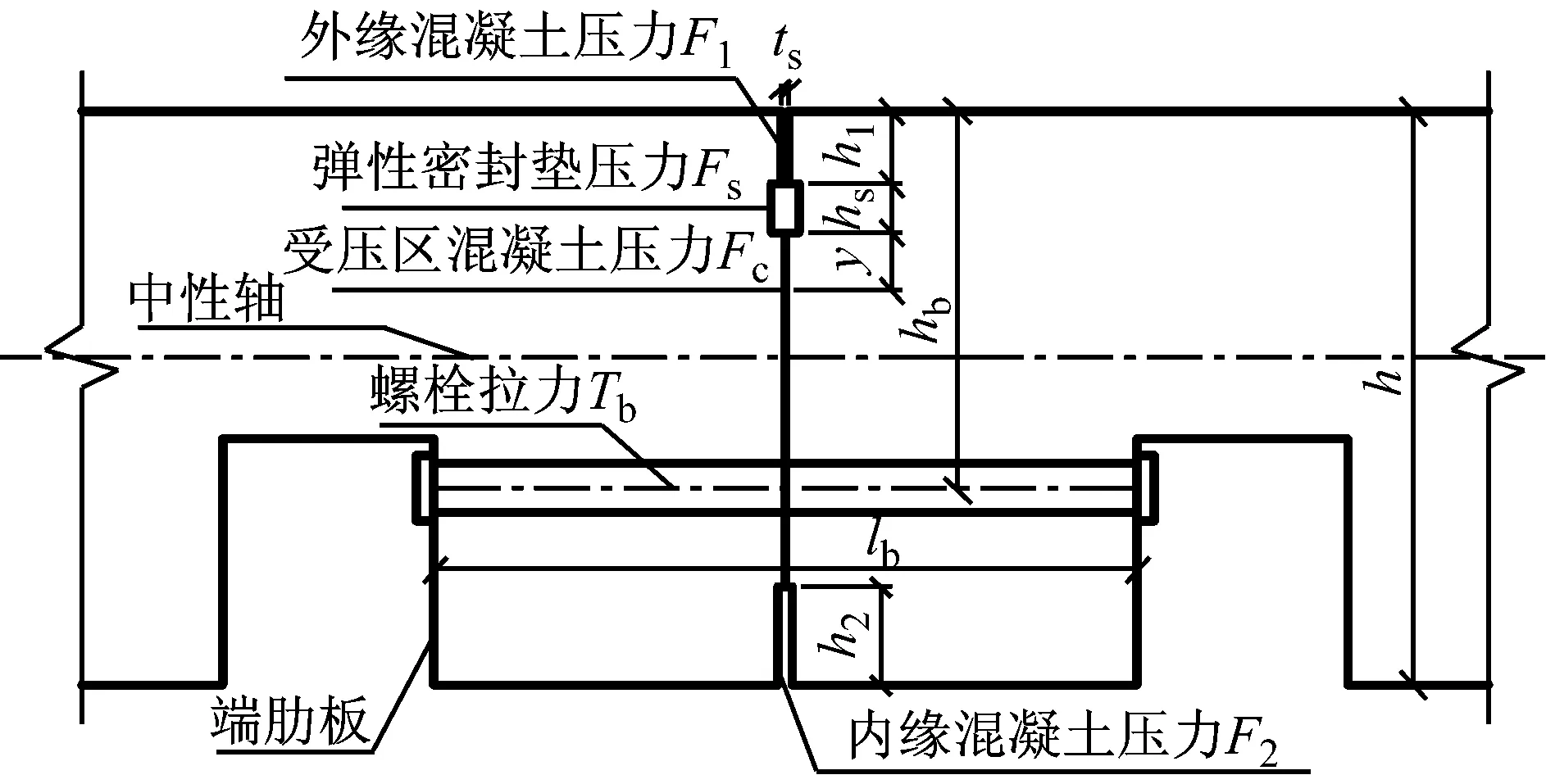
图4　接头几何尺寸图Fig.4　Geometry of segment joint

图中混凝土管片厚度h为350 mm，管片嵌缝槽宽度ts为4 mm，外嵌缝槽深度h1为44 mm，内嵌缝槽深度h2为60 mm.螺栓长度lb为400 mm，直径30 mm，螺栓距混凝土外边缘的距离hb为230 mm.

考虑混凝土端肋对螺栓刚度的折减，螺栓与端肋连接刚度的计算参考村上-小泉方法[16].端肋混凝土受螺栓端部挤压时，与螺栓共同作用，且变形较大，因此在计算接头变形时，端肋混凝土的压缩变形不可忽略.计算螺栓与端肋连接刚度时，应考虑这部分混凝土变形的影响.把端肋混凝土的局部压缩部分看作一压缩弹簧，弹簧的长度取为端肋厚度的一半.

(2)

(3)

ru=rw+t/12

(4)

式中:E为混凝土的弹性模量;Au为压缩区域有效面积;t为端肋厚度;ru为压缩有效区半径;rw为螺母半径;ra为螺栓孔半径.

由于端肋所受的压力与螺栓受力相同，接头总变形量为螺栓和接头两边端肋变形之和.把两个端肋压缩弹簧和螺栓相串联，得到的刚度即为螺栓和端肋的连接刚度K

(5)

Kb=EbA/lb

(6)

根据式(2)～(6)，可计算得螺栓的等效弹性模量Eb=0.88×105MPa.

弹性密封垫材料采用三元乙丙橡胶，闫治国等[17]通过模型试验，获得弹性密封垫的本构关系公式为

Fs=

(7)

式中:Δ为弹性密封垫压缩量,mm.

2.3接头抗弯力学分析

2.3.1接头抗弯力学模型及分析

当接头受到的弯矩较小时，只有中部混凝土直接接触.随着弯矩的增加，接头的变形不断增加，嵌缝槽外缘混凝土进入工作状态，产生一定抗力，接头的刚度增加.在已知接头轴力和弯矩的情况下，讨论嵌缝槽外缘混凝土是否接触，联立力平衡方程和弯矩平衡方程，求解接头的几何变形情况.

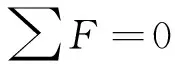
(8)

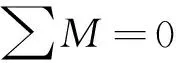
(9)

具体地，接头受力可分为以下几个阶段:

(1)嵌缝槽外缘混凝土尚未接触

N+Tb-Tc-Fs=0

(10)

M-Fcyc-Tbhb-Fs(h1+0.5hs)=0

(11)

式中:Fc为接头中部混凝土压应力的合力；Tb为螺栓拉力；Fs为弹性密封垫压力；N为接头所受的轴力；yc为混凝土合力到嵌缝槽外缘的距离；hb为螺栓到嵌缝槽外缘的距离；M为接头所受的弯矩.

假设混凝土受压区深度为混凝土受压边缘到中性轴距离的两倍[16].受压区混凝土符合平截面假定，在脱离区上，不同脱离区各自形成平面，各点位移同样符合平截面假定，且截面转角相同.假设混凝土处于弹性阶段时，应力服从三角形分布，则

(12)

式中:Ec为混凝土弹性模量；y为混凝土受压边缘到中性轴的距离；Δc为混凝土受压边缘的变形量；L为管片宽度.

(2)嵌缝槽外缘混凝土接触

N+Tb-Tc-Fs-Fl=0

(13)

(14)

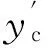
将接头受力及健康状况离散化.正负弯矩值分为0～75 kN·m，75～150 kN·m，150～225 kN·m，225～300 kN·m四级.其余变量分级如表4所示.

表4　接头抗弯模型受力和健康状况分级表Tab.4　Force and health state scales with bending moment

根据上述接头解析模型，可采用蒙特卡洛方法，获得大量计算案例，从而计算贝叶斯网络中关于接头抗弯性能的条件概率.蒙特卡洛法是通过用实验方法研究随机变量分布的有效方法.蒙特卡洛法经过反复实验、观测，取得随机变量的子样，然后用子样来估计待定的参数值.只要观测子样足够大，就会得到足够精确的结果.计算中，为保证各个工况有足够的计算样本且样本数量相当，本文假设弯矩、轴力、螺栓截面锈蚀率和混凝土强度折减均服从均匀分布，且每种工况计算1 000次.由此可以得到相应的条件概率表，如表5所示.

表5表示当混凝土强度折减为0～20%，螺栓截面锈蚀率为0～3%时，不同轴力和正弯矩作用下，混凝土和螺栓拉应力状态的概率分布情况.其中C1,C2,C3,B1,B2分别表示混凝土和螺栓的不同应力安全等级.

由表5可得，混凝土和螺栓的健康状况相同时，随着弯矩的增加，接头处混凝土和螺栓的受力状况会恶化.在弯矩恒定的情况下，轴力减小，轴力偏心距变大，导致混凝土受到的压应力和螺栓受到的拉应力增加，从而对混凝土和螺栓产生不利影响.

类似地，通过相同的方法，可以得到在不同的接头健康状况下，混凝土和螺栓的应力状态随轴力和弯矩变化的条件概率表.由于篇幅原因，其余17张表格在此省略.通过分析可知，混凝土强度折减和螺栓截面锈蚀率的增加均不利于接头混凝土和螺栓的受力.弯矩较小时，混凝土强度折减的影响更大，随着弯矩的增加，螺栓锈蚀率的不利影响逐渐变大.

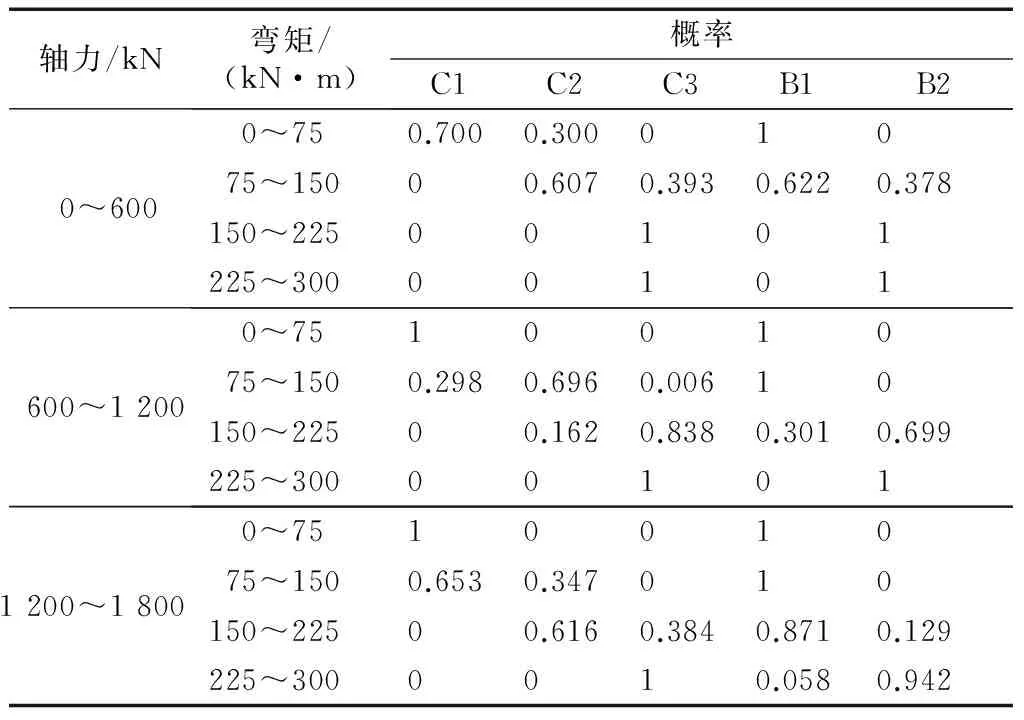
表5　接头受弯安全状况概率表Tab.5　Probability under bending moment

2.3.2抗弯模型数值模拟验证

为证明本文提出的接头力学模型假设的合理性以及计算结果的准确性，本文通过ABAQUS 6.10建立了环向接头精细化实体模型.混凝土和螺栓的应力应变关系、管片和螺栓的尺寸参数分别如图1、图2和图4所示.为简化计算，模型采用半结构，并以直梁代替曲梁计算[18].模型两端采用简支梁支座边界条件，并约束对称面.受力示意图如图5所示.图中,FN为受压荷载,FM为受弯荷载.模型网格图如图6所示，计算结果对比如图7和图8所示.

图5　接头受弯示意图Fig.5　Joint with bending moment

图6　数值模拟模型图Fig.6　Numerical simulation model

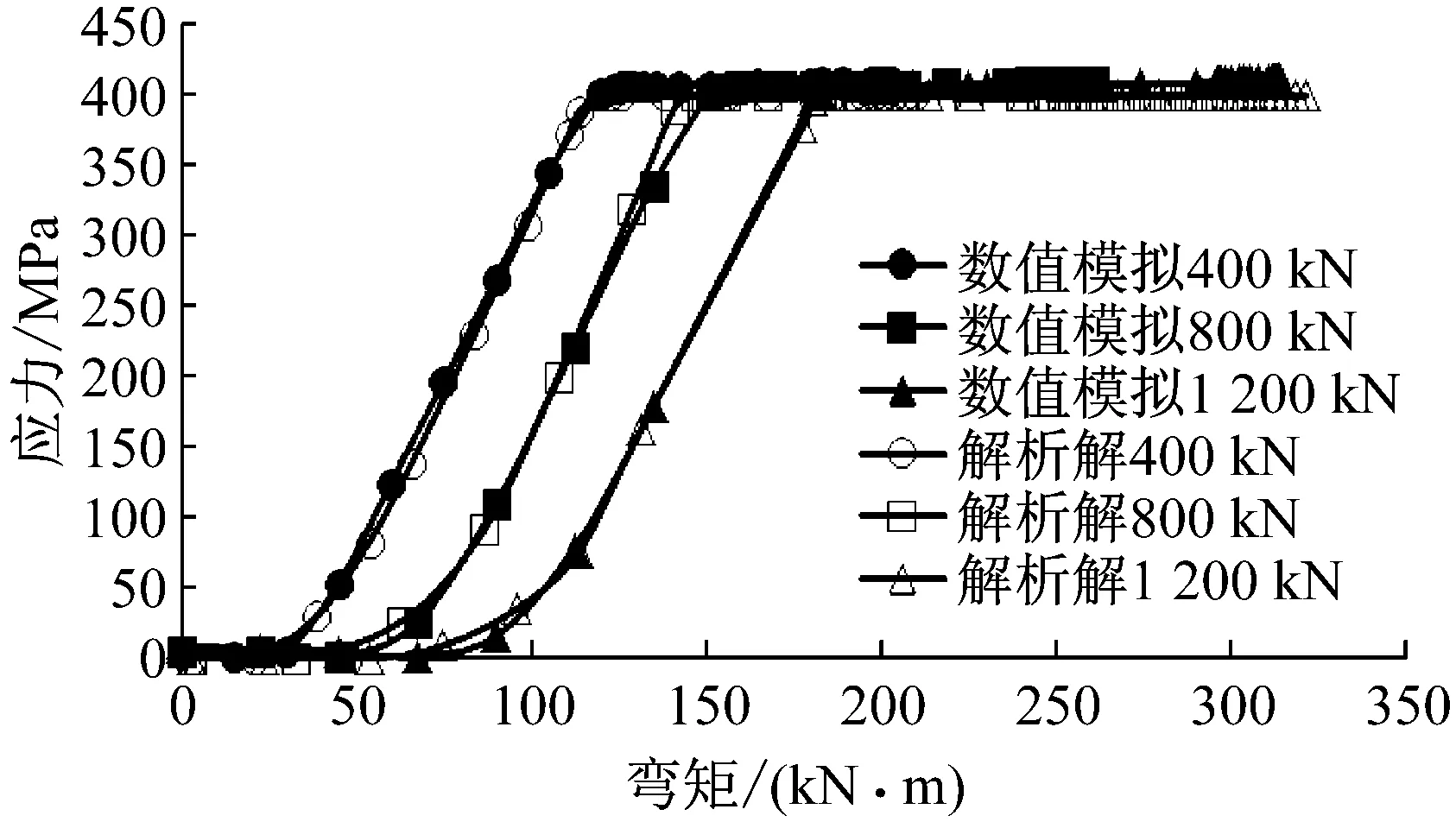
图7　螺栓拉应力对比图Fig.7　Comparison of bolt tensile stress

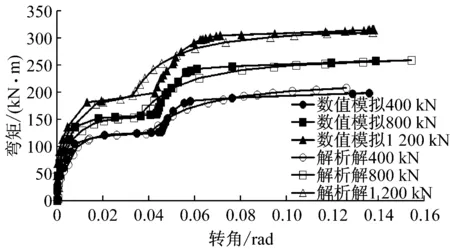
图8　 接头转角对比图Fig.8　Comparison of rotation of joint

图7表示在轴力为400,800,1 200 kN三种工况下，螺栓拉应力与接头所受弯矩之间的关系，并对比了数值模拟和解析求解结果.由图7可知，解析解与有限元模拟的螺栓应力状况较为一致.图8表示在轴力为400,800,1 200 kN三种工况下，接头转角与接头所受弯矩之间的关系.根据图8，可将接头受弯变形分为四个阶段:第一阶段,接头混凝土和螺栓均处于弹性阶段，接头刚度较大，抗弯能力较强;第二阶段,混凝土和螺栓相继屈服，接头的抗弯刚度迅速下降，接头变形迅速增加;第三阶段,由于接头受弯产生了较大的转角，导致嵌缝槽外缘混凝土参加受力，接头的刚度又逐渐增加;第四阶段,接头嵌缝槽外缘混凝土亦进入屈服阶段，接头抗弯刚度再次下降，接头变形进一步增加，直至完全破坏.解析求解能较好地模拟接头弯矩-变形图的两个台阶，到达台阶处的弯矩与数值模拟的结果基本一致，可以认为解析求解的结果是可靠的.

2.4接头抗剪力学分析

接头因剪力作用产生的效应，可简化为四个阶段：第一阶段，所受剪力小于接头混凝土因轴向受压产生的最大摩擦力；第二阶段，所受剪力大于等于接头混凝土因轴向受压产生的摩擦力，接头接触面发生相对滑动，但螺栓尚未与螺栓孔壁接触；第三阶段，接头错台达到12 mm，即螺栓与螺栓孔壁接触，螺栓开始受剪；第四阶段，螺栓受剪破坏，孔壁受压破坏，接头无法继续抗剪.

上述第三阶段的受力公式如下：

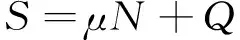
(15)

式中:μ取0.5;N为接头所受的轴力;S为接头所受的剪力;Q为螺栓所受的剪力.

螺栓受剪的力学模型如图9所示[19].图中，l为螺栓长度，Q为螺栓所受的剪力，δ为剪力接触点的距离，r为螺栓半径.螺栓所受的最大剪应力可按下式计算：

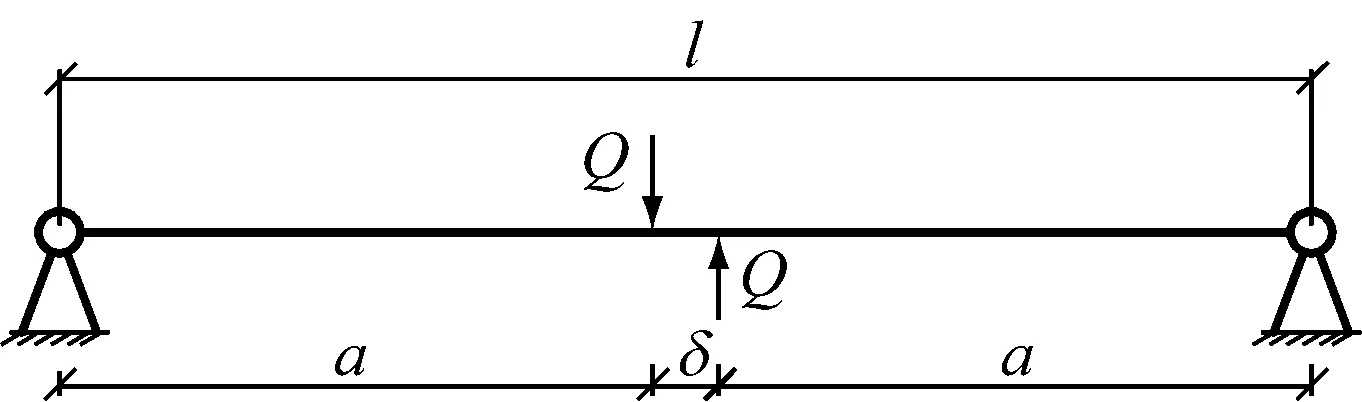
图9　集中荷载假设下螺栓求解示意图Fig.9　Bolt with centralized shear force

(16)

将接头受力及健康状况离散化，具体分级见表6.

表6　接头抗剪模型受力和健康状况分级Tab.6　Force and health state scales with shear force

在不同工况下，进行蒙特卡洛计算，假设剪力、轴力、螺栓截面锈蚀率均服从均匀分布，且每种工况计算1 000次.由此可以得到相应的条件概率表，如表7所示.

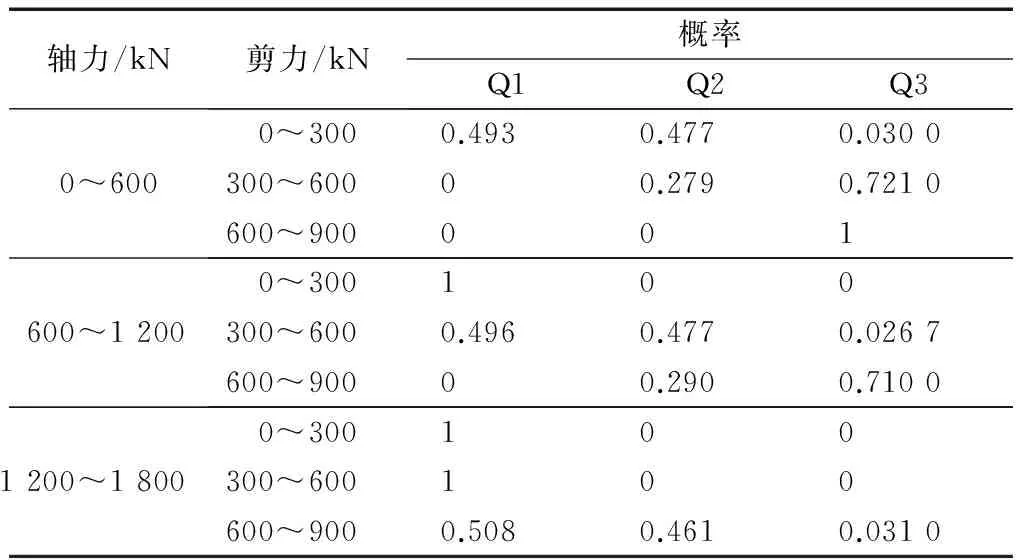
表7　接头受剪安全状况概率表Tab.7　Probability under shear force

表7表示当螺栓截面锈蚀率为0～3%时，不同轴力和剪力作用下，螺栓受剪状态的条件概率情况.其中Q1，Q2，Q3分别表示螺栓的安全等级.

由表7可得，在螺栓截面锈蚀状况相同时，随着剪力的增加，接头连接螺栓的受剪应力状况会逐渐恶化.随着轴力的增加，接头混凝土之间的摩擦力增加，螺栓承担的剪力减小，接头抗剪偏于安全.

通过相同的方法，可以得到不同的螺栓截面锈蚀率下，接头处螺栓的剪应力状态随轴力和剪力变化的条件概率表.由于篇幅原因，其余两张表格在此省略.通过计算表明，螺栓截面锈蚀率的增加也会对接头螺栓的受剪性能产生不利的影响.

2.5接头抗渗分析

盾构隧道管片接头的抗渗能力与接头处的弹性密封垫的工作状况有着非常紧密的关系.其中弹性密封垫的抗水压能力与接触面的压力和错位量有关.本文根据模型在不同轴力、弯矩、剪力以及混凝土强度折减和螺栓截面锈蚀率下的接头变形，评价接头的抗渗易损性.当接头张开量大于6 mm，或者管片间错动大于8 mm时，接头抗渗漏水性能受到较大影响，由此可以得到与上节类似的条件概率表.

表8表示当螺栓截面锈蚀率为0～3%，混凝土强度折减为0～20%，接头所受轴力为600～1 200 kN时，不同弯矩和剪力作用下，接头渗漏水等级的概率分布情况.其中S1，S2分别表示接头渗漏水的安全等级.

表8　接头渗漏水安全状况概率表Tab.8　Probability of seepage of joint

由表8可得，在螺栓截面锈蚀状况、混凝土强度折减以及接头所受轴力相同时，随着弯矩的增加，接头逐渐张开，弹性密封垫所受压力下降，弹性密封垫的隔水性能下降，接头渗漏水状况会逐渐恶化.接头所受剪力的增加可能会使接头产生较大的切向变形，导致弹性密封垫无法正常工作，接头产生渗漏水.

通过相同的方法，可以分析螺栓截面锈蚀率、混凝土强度折减以及接头所受轴力对接头渗漏水的影响.由于篇幅原因，其余26张表格在此省略.计算表明，螺栓截面锈蚀率、混凝土强度折减以及接头所受轴力均会影响接头的抗渗性能.

3　接头易损性的应用案例分析与检验

3.1接头易损性应用分析

由上节对接头抗弯、抗剪、抗渗三方面的易损性分析，可获得贝叶斯网络的条件概率表.本文利用NETICARR 5.12软件，构建接头易损性贝叶斯网络，分析各因素对盾构隧道管片接头易损性的影响.图10和图11表示不同弯矩作用下，接头易损性的贝叶斯网络图.由于轴力、剪力、以及混凝土和螺栓的健康状况未知，假设各个等级的先验概率均为0.33.图中，各参数具体分级如第2节所述.

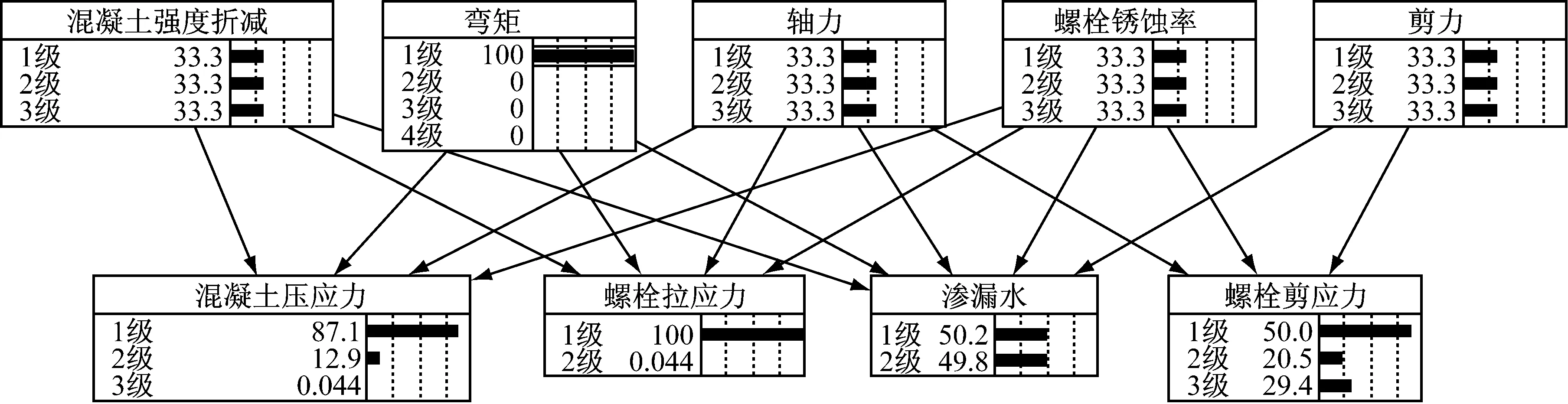
图10　小弯矩下贝叶斯网络图Fig.10　Bayes-network with small bending moment

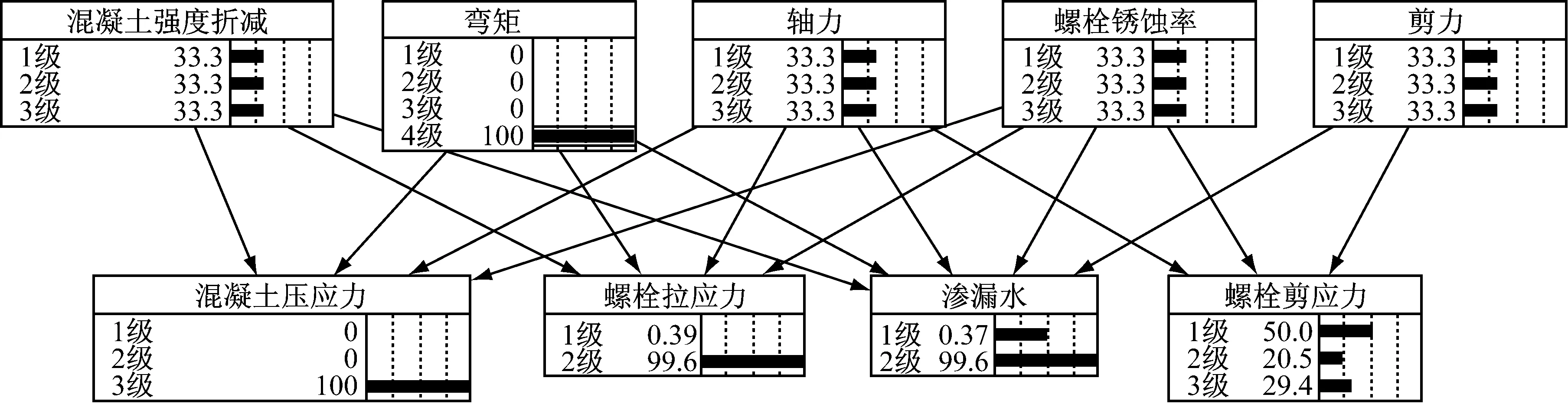
图11　大弯矩下贝叶斯网络图Fig.11　Bayes-network with large bending moment

对比图10和图11可知，接头受到的弯矩对接头的受力和变形影响很大.如图10所示，当侧压力系数较小，衬砌环所受土压力较为均匀时，接头所受的正弯矩较小.此时，混凝土应力为1级的概率为87.1%，螺栓拉应力为1级的概率为100%，均处于相对安全的状态，接头易损性较小.相反，如图11所示，当侧压力系数较大，衬砌周边土体不能提供足够的水平抗力，从而产生横鸭蛋效应时，接头所受的弯矩增加至4级，混凝土应力为3级的概率为100%，螺栓拉应力为3级的概率为99.6%，均处于非常危险的状态，接头易损性增加.此外，由于接头受弯严重，接头处产生了较大的张开量，接头的抗渗漏水性能削弱，产生渗漏水的概率大大增加，渗漏水达到2级的概率为99.6%.

同理，可分析接头结构自身的健康状况(包括接头处混凝土强度折减和螺栓截面锈蚀率)，对接头易损性的影响.当接头所受弯矩较小时，混凝土强度折减对接头易损性的影响大于螺栓锈蚀率的影响，随着弯矩的逐步增加，螺栓锈蚀率的影响明显变大.说明当弯矩较小时，弯矩主要由接头混凝土承担，然而，当弯矩变大，即产生较大的偏心压力，混凝土受压面逐步减小时，螺栓起主要的抗弯作用，此时，螺栓截面锈蚀率对接头易损性的影响很大.一般情况下，接头处混凝土被局部压溃早于螺栓受拉屈服，接头处混凝土的易损性大于螺栓的易损性.当螺栓屈服时，接头会产生较大变形，很大程度上，增加了接头的抗渗易损性.当接头弯矩为负弯矩时，也有类似的规律.但是由于此时螺栓能提供的力矩较小，接头的抗弯性能比受正弯矩作用时弱，接头处混凝土被压溃的概率变大，易损性增加.接头的抗剪易损性受剪力和轴力的影响较大，接头螺栓截面锈蚀率的增加会对接头的抗剪性能造成不利影响.

3.2接头病害实例分析

本文选取某运营盾构隧道作为实例分析.该隧道所处的地质条件如图12所示.

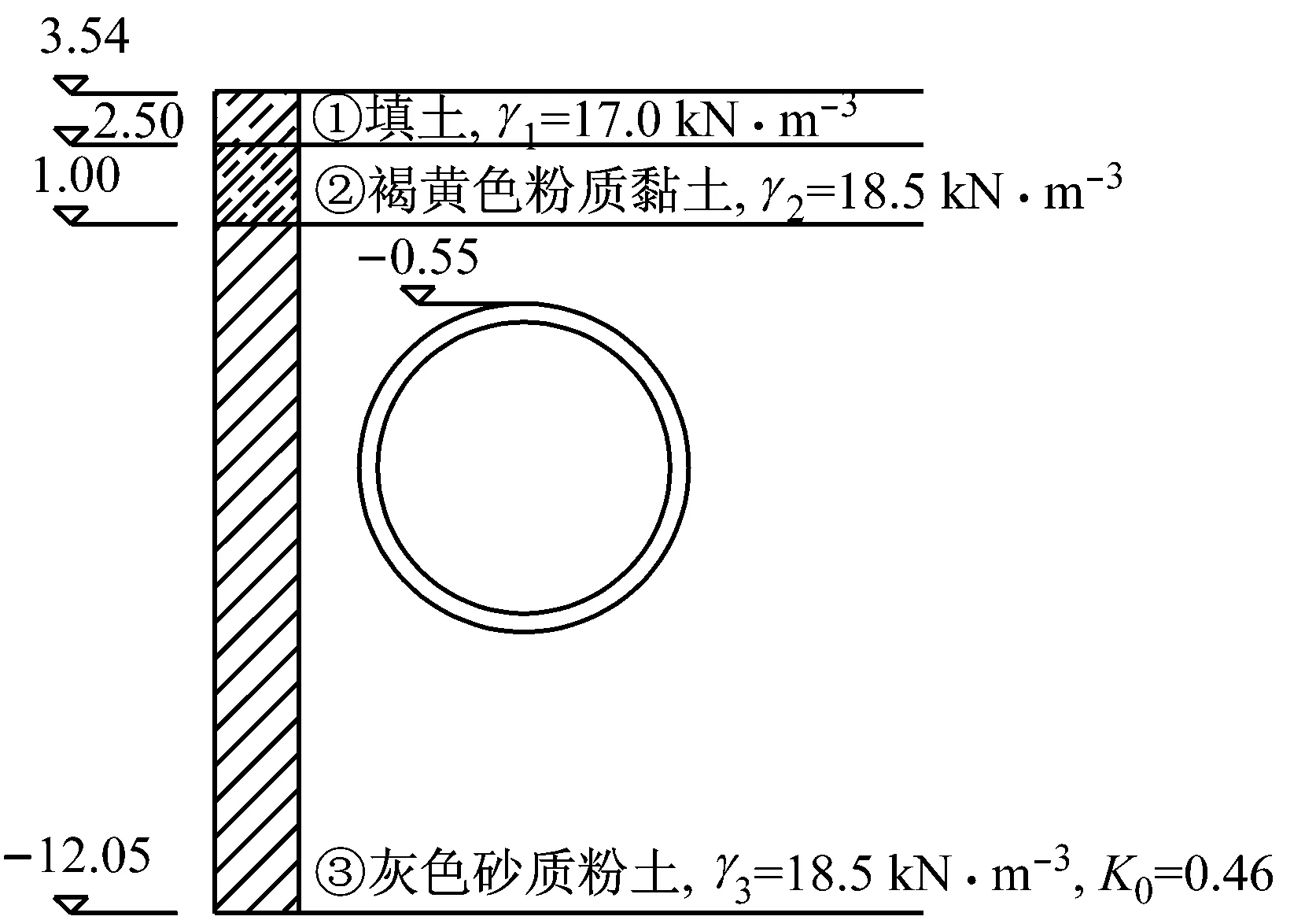
图12　隧道剖面图(高程单位:m)Fig.12　Profile of tunnel position(elevation unit: m)

经计算可得，封顶块和邻接块之间的接头所受正弯矩为49.07 kN·m，小于限值75 kN·m；轴力154.50 kN，小于限值600 kN；剪力8.84 kN，小于限值300 kN；由于未知管片混凝土的健康状况和螺栓的锈蚀情况，假设均匀分布.通过贝叶斯网络分析接头易损性，如图13所示.

由图13可知，在管片混凝土的健康状况和螺栓的锈蚀率未知的情况下，该处盾构隧道螺栓受拉屈服的可能性较小，螺栓为1级的概率为99.9%，但是接头渗漏水为2级的概率为48.9%，螺栓剪应力为2级的概率为45.4%.可以认为，该处接头可能产生渗漏水，且有一定的错台.

为提高贝叶斯网络的实用性，增加置信度，可以根据现场监测的数据，对贝叶斯网络进行信念更新，从而提高网络的可信度，增加实用性.

如果通过实地监测等方法，检测到接头处有渗漏水，且产生了较大的错台，可更新该贝叶斯网络，如图14所示.图14表示，根据现场监测数据，贝叶斯网络可反分析接头结构的健康状况.混凝土存在损伤的概率略有增加，且螺栓存在锈蚀的概率较大，螺栓锈蚀率为3级概率达到了52.2%，需要及时检查螺栓的锈蚀情况，保证隧道的正常运营.

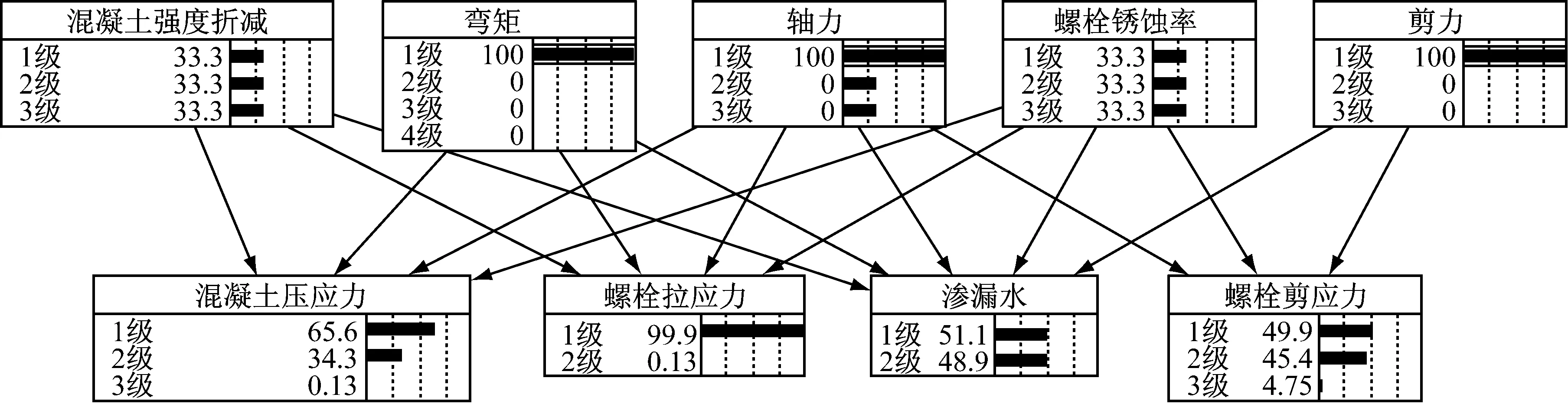
图13　贝叶斯网络实例分析Fig.13　Case study by Bayes-network

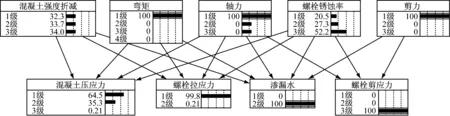
图14　贝叶斯网络更新实例分析Fig.14　Case study by updated Bayes-network

4　结论

(1)接头受正弯矩作用时，混凝土强度折减和螺栓截面锈蚀率的增加都会对接头混凝土和螺栓的受力产生不利的影响.轴力较大时，混凝土强度折减的影响比轴力较小时显著.混凝土强度折减的影响主要集中在弯矩较小时，随着弯矩逐渐增加，螺栓锈蚀率的不利影响逐渐增加.一般情况下，接头处混凝土被局部压溃早于螺栓受拉屈服，因此接头处混凝土的易损性大于螺栓的易损性.

(2)接头受负弯矩作用时，接头的力学性能与正弯矩下相近.但由于此时螺栓能提供的力矩较小，接头的抗弯性能比受正弯矩作用时差，接头处混凝土被压溃的概率变大，易损性增加.

(3)接头抗剪易损性随轴力的增加而减小，随螺栓锈蚀率的增加而变大.

(4)接头抗渗易损性与接头弹性密封垫、嵌缝槽的工作状况和混凝土完整性等因素关系紧密.接头处剪力、弯矩、混凝土强度折减和螺栓截面锈蚀率的增加均会对接头抗渗易损性产生不利影响.

(5)运用贝叶斯网络的信念更新功能，结合现场监测，可更新接头易损性预测，反分析盾构隧道管片接头的病害成因.

[1]Lee K M，Hou X Y，Ge X W，etal. An analytical solution for a jointed shield-driven tunnel lining[J]. International Journal for Numerical and Analytical Methods in Geomechanics， 2001，25：365．

[2]张冬梅，樊振宇，黄宏伟. 考虑接头力学特性的盾构隧道衬砌结构计算方法研究[J]. 岩土力学，2010，31(8)：2546.

ZHANG Dongmei，FAN Zhenyu，HUANG Hongwei. Calculation method of shield tunnel lining considering mechanical characteristics of joints [J]. Rock and Soil Mechanics，2010，31(8)：2546.

[3]林光俊. ほぞセグメトの力学特性おょびその合理的製造方法に関すゐ研究[D]. 东京：早稻田大学，1997.

[4]ZHANG Wenjun, Koizumi A. Behavior of composite segment for shield tunnel [J]. Tunnelling and Underground Space Technology，2010(25)：325.

[5]郭瑞，何川，苏宗贤，等. 盾构隧道管片接头抗剪力学性能研究[J]. 现代隧道技术，2011，48(4)：72.

GUO Rui，HE Chuan，SU Zongxian，etal. Study of shearing mechanical properties of segment joints of shield tunnels[J]. Modern Tunneling Technology，2011，48(4)：72.

[6]赵明，丁文其，彭益成，等. 高水压盾构隧道管片接缝防水可靠性试验研究[J]. 现代隧道技术，2013，50(3)：87.

ZHAO Ming，DING Wenqi，PENG Yicheng，etal. Experimental study on the reliability of shield tunnel segment joints to remain watertight under high water pressure[J]. Modern Tunneling Technology，2013，50(3)：87.

[7]李剑. 盾构公路隧道结构性能检测评估指标及应用研究[J]. 地下空间与工程学报，2012,8(3)：549.

LI Jian. Applied research of index of the investigation and evaluation of the serviceability of the road shield tunnel[J]. Chinese Journal of Underground Space and Engineering，2012，8(3)：549.

[8]HUANG Xu，HUANG Hongwei. Vulnerability evaluation of shield tunnel under the effect of above excavation[C]∥Proceeding of international symposium on tunnelling and underground space construction for sustainable development. Seoul: CIR，2013：160-164.

[9]于刚，孙利民. 断索导致的斜拉桥结构易损性分析[J]. 同济大学学报:自然科学版，2010，38(3)：312.

YU Gang，SUN Limin. Vulnerability analysis of cable-stayed bridge due to cable failures [J]. Journal of Tongji University:Natural Science，2010，38(3)：312.

[10]Saeidi A, Deck O, Verdel T. Development of building vulnerability functions in subsidence regions from analytical methods[J]. Geotechnique, 2012, 62(2): 107.

[11]Sousa R L, Einstein H H. Risk analysis during tunnel construction using Bayesian networks: Porto Metro case study [J]. Tunnelling and Underground Space Technology， 2012，27：86．

[12]周健，王红卫，吴邵海. 盾构法施工风险的多态贝叶斯网络模型分析[J]. 同济大学学报:自然科学版，2013，41(2)：186.ZHOU Jian，WANG Hongwei，WU Shaohai. Risk analysis of shield construction by polymorphic of Bayesian networks model[J]. Journal of Tongji University:Natural Science，2013，41(2)：186.

[13]Hwang H，刘晶波. 地震作用下钢筋混凝土桥梁结构易损性分析[J]. 土木工程学报，2004，37 (6)：47.

Hwang H，LIU Jingbo. Seismic fragility analysis of reinforced concrete bridges[J]. China Civil Engineering Journal，2004，37 (6)：47.

[14]张厚美，张正林，王建华. 盾构隧道装配式管片接头三维有限元分析[J]. 上海交通大学学报，2003，37(4)：566.

ZHANG Houmei，ZHANG Zhenglin，WANG Jianhua. 3-D FEM analysis on prefabricated segment joints of shield tunnel [J]. Journal of Shanghai Jiaotong University，2003，37(4)： 566.

[15]王如路，肖同刚，朱妍. 上海地铁盾构隧道渗漏水治理与变形控制[J]. 地下工程与隧道，2007(2)：102.

WANG Rulu，XIAO Tonggang，ZHU Yan. Water leakage and deformation control of shield tunnel in Shanghai metro[J]. Underground Engineering and Tunnel，2007(2)：102.

[16]小泉淳. 盾构隧道管片设计[M]. 北京：中国建筑工业出版社，2012.

KOIZUMI Atsushi. Design of shield tunnel segment [M]. Beijing：China Architecture & Building Press, 2012.

[17]闫治国，丁文其，沈碧伟，等. 输水盾构隧道管片接头力学与变形模型研究[J]. 岩土工程学报，2011，33(8)：1186.

YAN Zhiguo， DING Wenqi，SHEN Biwei，etal. Structural model for radial joints of water-conveyance shield tunnels[J]. Chinese Journal of Geotechnical Engineering，2011，33(8)：1186.

[18]曾东洋, 何川. 地铁盾构隧道管片接头抗弯刚度的数值计算[J]. 西南交通大学学报，2004，39(6)：744.

ZENG Dongyang，HE Chuan. 3-D FEM analysis on prefabricated segment joints of shield tunnel [J]. Journal of Xinan Jiaotong University，2004，39(6)： 744.

[19]黄钟晖，廖少明，侯学渊. 错缝拼装衬砌纵向螺栓剪切模型的研究[J]. 岩石力学与工程学报，2004，23(6)：952.

HUANG Zhonghui，LIAO Shaoming，HOU Xueyuan. Research on shear model of ring joint bolts in stagger-jointed segmental linings [J]. Chinese Journal of Rock Mechanics and Engineering，2004，23(6)：952.

Vulnerability Analysis and Assessment of Segmeng Joints in Shield Tunnel

HUANG Hongwei1,2， SHEN Xianda1,2， WANG Fei3， ZHANG Dongming1,2

(1. College of Civil Engineering， Tongji University， Shanghai 200092， China； 2. Key Laboratory of Geotechnical and Underground Engineering of the Ministry of Education， Tongji University， Shanghai 200092， China； 3. Shanghai Institute of Disaster Prevention and Relief， Shanghai 200092， China)

Joints of shield tunnels are the weak but key elements of the whole structure. Considering the resistance capacity to bending moment, shear force and seepage, assessment of the vulnerability of shield tunnel segment joints was conducted and a model of vulnerability evaluation of segment joints subjected to inner forces was established under the consideration of the health state of joints. The stress of segment concrete and bolts, and seepage were taken as the assessment criteria of the model. Then, an analytical joint model was established to analyze the mechanical response of joints, and verified by the 3D refined numerical simulation. Based on a large number of learning cases offered by Monte Carlo simulation analysis, Bayesian networks were employed to evaluate the vulnerability of segment joints. Based on in-situ monitoring data, the back analysis of health state of shield tunnel segment joints and the updated prediction of the vulnerability of segment joints are applied to help the operation and maintenance of shield tunnels.

shield tunnel; segment joint; vulnerability analysis; Bayes-network

2015-03-03

国家自然科学基金(51278381，51538009)；交通部建设科技项目(2015318J31060)

黄宏伟(1966—)，男，教授，工学博士，主要研究方向为隧道及地下工程风险分析与评估.E-mail: huanghw@tongji.edu.cn

TU451

A