TJ-1模拟月壤承载特性物理模型试验研究

蒋明镜， 奚邦禄， 孙德安， 王　闯

(1.同济大学 土木工程学院，上海 200092； 2.上海大学 土木工程系，上海 200072； 3.中国空间技术研究院，北京 100094)



TJ-1模拟月壤承载特性物理模型试验研究

蒋明镜1， 奚邦禄1， 孙德安2， 王闯3

(1.同济大学 土木工程学院，上海 200092； 2.上海大学 土木工程系，上海 200072； 3.中国空间技术研究院，北京 100094)

借助现代土力学试验技术研究月壤工程特性，是解决月球上岩土工程问题的一个可行方法.室内载荷物理模型试验是研究土体承载特性的重要方法.本研究自行设计加工了一套可以实现加载速率控制的加载装置，采用试验材料为Tongji-1(简称TJ-1)模拟月壤，对4种不同尺寸的圆盘载荷板进行加载速率控制条件下的载荷模型试验，同时测定了基底土压力分布.试验结果表明：在相同载荷板条件下，TJ-1模拟月壤的地基极限承载力和变形模量随加载速率的增加而增加；在相同加载速率条件下，TJ-1模拟月壤的地基极限承载力和变形模量随载荷板尺寸增加而增加；加载时基底中心土压力最大.

微地基承载力； TJ-1模拟月壤； 载荷试验； 载荷速率影响； 载荷板尺寸影响

欧阳自远院士提出在我国月球探测第 3 期工程完成月面巡视勘察与采样返回，基本完成不载人月球探测任务后, 根据我国的国情和国力, 实施载人登月和月球基地的建设[1].国内外许多学者关于月球基地的设计进行相关研究[2-3].从岩土工作者角度出发，在月球基地的设计中，需要明确月壤的承载力特性，优化地基基础设计，减少材料消耗，降低月球基地建设成本，为月面工程建设提供参考.

月壤是在氧气、水、风和生命活动都不存在的情况下，通过陨石和微陨石撞击、宇宙射线和太阳风持续轰击、大幅度昼夜温差变化导致岩石热胀冷缩破碎共同作用引起的.月壤的主要矿物成分包括长石、辉石和橄榄石.根据真实月壤级配曲线，月壤可归类于粉质砂土[1].然而根据美国Apollo计划和前苏联luna计划中所实施的大量现场试验以及对带回地球的真实月壤样品试验可知，真实月壤内摩擦角φ=25°～50°，黏聚力c=0.26～1.80 kPa[4-5].而地球上砂土黏聚力一般认为是0.有关研究表明，月壤黏聚力来源于分子间作用力(范德华力).月面环境下大气层极为稀薄，在地球上无需考虑的分子间作用力在月面环境下则需要考虑[6-7].

地基承载特性是土体工程力学性能的重要指标之一，可以通过室内载荷板试验确定.考虑到直接在月面进行其承载特性研究是不现实的，而且地球上真实月壤含量极少，无法大量用于月壤承载力特性研究.多数学者采用模拟月壤，一种具有与月壤相似的矿物组成、化学成分和物理力学性质的地球物质进行相关的试验研究.Kobayashi等[8]研究了不同重力作用下浅基础在FJS-1模拟月壤地基上的荷载-沉降特性，结果表明FJS-1模拟月壤和Toyoura砂破坏模式并不相同，基于塑性力学理论的经典承载力理论并不一定适用于月壤的承载力预测，并在此基础上提出一种新的理论模型，该模型考虑了重力场对月壤破坏模式的影响，可以较好地预测月面环境下地基承载力的大小[9].Bui等[10]利用飞机俯冲获得短时间低重力场研究了不同重力加速度下Toyoura砂和FJS-1模拟月壤的承载力问题，结果表明重力加速度对Toyoura砂的承载力影响显著，然而重力加速度小于1个g时，重力加速度对FJS-1模拟月壤承载力无明显影响.Perkins和Madson[11]采用离心机试验研究了MLS-1和JSC-1模拟月壤浅基础时荷载-沉降特性，结果表明两种模拟月壤的地基承载力和变形模量均随地基宽度增加而增加.蒋明镜等[12]在13 m×12 m×1.2 m试验用TJ-1(Tongji-1)模拟月壤地基上进行了静力触探试验和静载荷试验，并将试验结果与国内外12种承载力公式对比，发现太沙基半经验公式无法准确预测TJ-1模拟月壤的地基承载力.邹猛等[13]通过压板试验获取了3种不同粒径分布模拟月壤的承压性能曲线与参数，分析了粒径分布对于模拟月壤承压性能的影响，结果表明粒径粗且分布均匀的模拟月壤承压能力最强.

模拟月壤地基承载力的试验研究都是在室内物理模型箱内进行的，载荷板的尺寸和加载速率对于模拟月壤的承载力特性影响很大.因此有必要研究载荷板尺寸和加载速率对模拟月壤地基承载力的影响.本文以TJ-1模拟月壤为原材料，自行设计加工了一套可以实现不同加载速率控制的试验加载装置,以其进行载荷板试验，共使用4种不同直径的圆盘载荷板，进行了不同加载速率条件下的TJ-1模拟月壤的载荷模型试验.同时，为了研究基底面的土压力分布，在直径为120 mm的圆盘底面布置了土压力计，以便在载荷试验过程中进行基底面土压力的实时测量.月壤的承载特性受月壤的基本力学特性、重力环境、加载方式等多种条件的影响，本文从可操作性的角度出发，研究地面环境下模拟月壤的承载特性，将试验成果借助理论分析及数值模拟推广到月面环境，为月球永久基地的设计提供参考性的数据[14-16].

1　试验概况

1.1试验材料

本次试验采用同济大学研制的TJ-1模拟月壤作为试验材料.该模拟月壤是以吉林省靖宇县境内的红色火山灰为母体材料，主要矿物成分为橄榄石、辉石、长石，并含有大于30%的玻璃体，经过烘干、粉碎、筛分最终获得符合目标力学指标的干燥模拟月壤材料，其颗粒形态较为粗糙，颗粒间存在较大咬合力，因此可以表现出较小黏聚力.其级配曲线见图1[17-18].与国内外其他模拟月壤相比，TJ-1 模拟月壤具有级配更加稳定，较大孔隙比时抗剪强度高的特点，如表1所示.

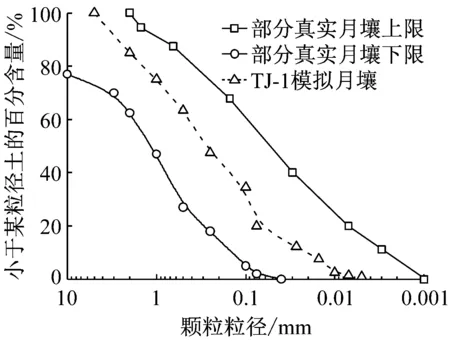
图1　TJ-1模拟月壤级配曲线[17-18]Fig.1　Gradation of TJ-1 lunar soil stimulant[17-18]表1　TJ-1模拟月壤主要物理力学指标Tab.1　Physical and mechanical indexes of TJ-1

物理力学指标数值含水率/%<1颗粒比重2.72有效粒径d10/μm平均粒径d50/μm20260不均匀系数21.5曲率系数0.92内摩擦角/(°)47.6黏聚力/kPa0.86压缩指数(法向力范围12.5～100.0kPa)0.086

1.2试验设备

本次试验使用同济大学地下建筑与工程系自行设计的模型箱[19]，其尺寸为1 500 mm×900 mm×900 mm，如图2所示.在该模型箱基础上，考虑到粒径效应和边界效应，圆盘直径取120,100,80,60 mm.在直径120 mm圆盘载荷板载荷试验中，板底面对称布置有5个直径为14 mm的土压力计，如图3所示.A位于基底中心，B1和B2距基底中心26mm，C1和C2距基底中心39 mm.

图2　模型箱[19]Fig.2　Model box[19]

图3　基底面土压力计的布置Fig.3　Arrangement of earth pressure cell in basal surface

1.3试验方案

本试验中的竖向位移加载速率通过调节电机频率来控制，载荷试验中电机频率分别取为5,10,15,20 Hz，其对应的平均位移加载速率分别约为1.9,4.6,7.2,9.5 mm·s-1.加载装置示意图如图4所示.在上述4种加载速率下进行TJ-1模拟月壤的地基极限承载力试验.试验过程中模型地基的干密度控制在1.36 g·cm-3左右.

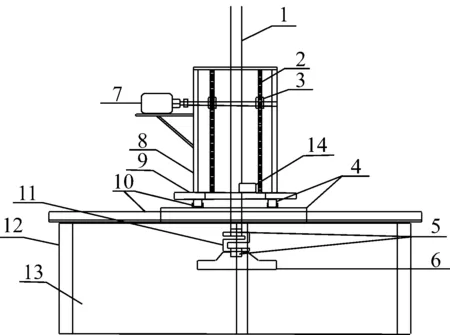
1-载入杆;2-链条;3-齿轮;4-滑块;5-连接杆;6-载荷板;7-电机;8-反力架;9-支座;10-导轨;11-传感器;12-导轨支撑;13-钢化玻璃;14-拉绳位移传感器

图4位移速率控制加载装置

Fig.4Loading device with displacement rate control

2　试验结果及分析

2.1基底平均压力与沉降量关系曲线

在不同直径基础条件下分别进行了不同加载速率下的载荷板试验，可用于研究分析载荷板尺寸及加载速率对TJ-1模拟月壤地基承载力的影响.本试验中分别使用不同直径圆盘载荷板进行了载荷试验，试验过程中记录p-s(基底平均压力-沉降量)曲线，其中p用载荷除以载荷板的面积进行计算.每组试验都进行多组平行试验取均值，以验证试验的正确性.所有的试验结果在表2中进行统计.图5为载荷板直径取100 mm、电机频率取10 Hz时4组平行试验的p-s曲线.由图可知,试验结果重复性较好，p-s曲线上有明显的拐点，可用于确定地基极限承载力;但仍有个别试验结果相差较大，如表2所示，这可能是由于试验过程中地基的密度不均匀所引起的.从p-s曲线的形式特征分析，地基的破坏模式更加接近于局部破坏模式.图6为电机频率5 Hz、加载速率约为1.9 mm·s-1时不同直径载荷板下的典型p-s曲线.可知，随着载荷板直径的增加，p-s曲线的形态基本相同，模拟月壤的承载力随载荷板直径的增加而增加，地基的破坏模式都更接近于局部破坏模式.图7为载荷板直径取120 mm，不同电机频率即不同加载速度下典型p-s曲线.可知，随着加载速率的增大，p-s曲线的拐点愈加明显，地基破坏模式逐渐从局部破坏模式发展为整体破坏模式，模拟月壤地基承载力随加载速率增大而增大.

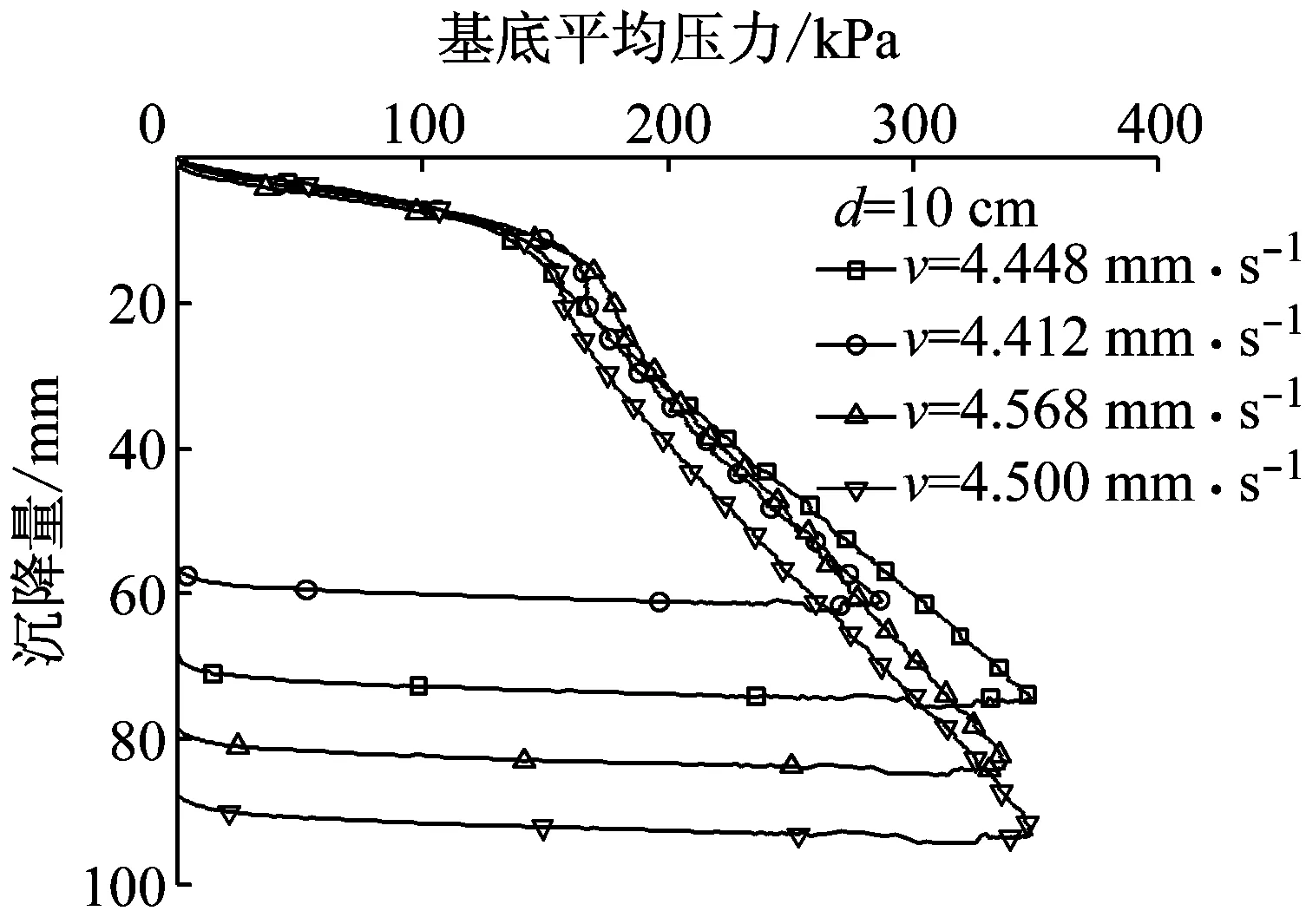
图5　平行试验结果Fig.5　Results of parallel tests

图6　不同载荷板尺寸试验结果Fig.6　Results with different loading plates

图7　不同加载速率试验结果Fig.7　Results with different loading rates

2.2地基极限承载力

分析表2数据可知，大多数试验结果重复性较 好，但6 cm直径加载板在平均加载速率7.384 mm·s-1时存在最终承载力相差较大的现象，这可能是由于试验条件差异(如地基局部不均匀等因素)引起的.在室内静载荷物理模型试验中，加载速率和基础尺寸均会对地基极限承载力产生影响.图8为不同直径载荷板时TJ-1模拟月壤的地基极限承载力与加载速率关系曲线.可知当圆盘直径相同时，模拟月壤地基承载力随加载速率增加而增加，且大致呈线性关系.常规地基承载力随加载速率增大而减小，可能与其孔隙水压难消散有关，本文研究中，TJ-1模拟月壤是干燥颗粒材料，无孔隙水压.加载速率相近时，模拟月壤地基承载力随载荷板直径的增加而增加，与Perkins等[11]结论相同.

图8　极限承载力加载速率关系曲线Fig.8　Ultimate bearing capacity vs loading rate

2.3地基变形模量

浅层载荷板试验中，地基土的变形模量E0可采用下式计算[20]:

(1)

式中:d为载荷板直径,m；Ι0为载荷板位于半空间表面的影响因子，对于圆形刚性板，Ι0=π/4=0.785；K为p-s关系曲线直线段斜率,kN·m-3，本文计算结果如表2所示；μ为土的泊松比，可通过式K0=1-sinφ′=μ/(1-μ)计算，其中，φ′为47.60°，可得μ=0.207 5≈0.21.根据式(1)和各参数的值，可计算得到各种载荷板在不同加载速率下的地基平均变形模量E0，如表3所示.图9为不同直径载荷板下TJ-1模拟月壤的平均变形模量与加载速率的关系曲线.在相同载荷板条件下，TJ-1模拟月壤的地基变形模量随加载速率的增加而增加；在相近加载速率下，TJ-1模拟月壤地基变形模量随着载荷板尺寸增加而增加.

表2不同加载速率下各种尺寸载荷板极限承载力

Tab.2Ultimate bearing capacity of loading plates with different sizes at different loading rates

直径/cm速率/(mm·s-1)平均速率/(mm·s-1)极限承载力/kPa平均极限承载力/kPa62.1322.1494.7704.8347.3617.4197.3729.9469.9002.1394.8027.3849.923125.78114.2115.85154.74105.92160.54123.30131.57172.12119.99135.30141.92151.8582.1452.0342.0214.9504.7624.7985.0004.6174.6417.1957.1689.4769.5682.0674.7647.1829.522131.73146.16160.59135.45135.92141.04146.16151.74170.83180.14168.97204.81175.95148.16152.44174.56190.38101.9501.9541.9051.8144.4484.4124.5684.5007.1367.0749.4119.4609.5611.9064.4827.1059.477165.74130.23126.61173.38176.66156.4165.63156.99199.60166.82173.97226.40166.82148.99163.92183.21200.19121.7701.4801.5034.5404.4844.3046.8576.9776.9959.0279.0989.4851.5844.4436.9439.203151.13183.50183.09162.19175.84190.74227.15194.26198.81267.70266.25226.81162.04176.26210.71253.59

表3　各载荷板在不同加载速率下的平均变形模量Tab.3　Mean deformation modulus

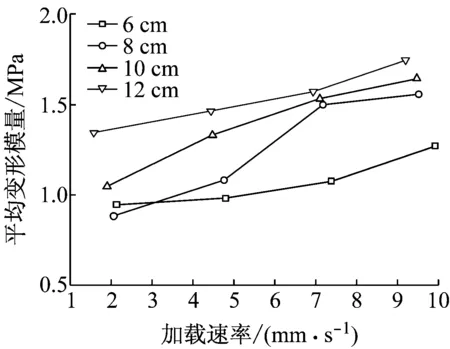
图9　变形模量加载速率关系曲线Fig.9　Deformation modulus vs loading rate

2.4基底土压力分布

基底对称布置5只土压力计，详见图3.各土压力计测得的基底土压力值随加载时间的变化如图10所示.从图可知，加载初期各点土压力增加较快，特别是中心点.图11为不同时刻的基底土压力分布.可知试验得到的载荷板底部的土压力分布具有很好的对称性，并且中心点的土压力明显更大，而距基底中心39 mm处的土压力值比距中心26 mm处的土压力值略大.由于本次试验采用的120 mm圆盘载荷板可视为刚性基础，地基土TJ-1模拟月壤为无黏性土，没有黏结强度.由于基础埋深很浅，因此在边缘处的土体几乎不具有抗剪强度.在荷载较小时，刚性基础对荷载的传递和地基的变形起约束和调节作用，因此在加载初期，基底面土压力分布较为均匀，形成类似于马鞍形的分布.随着荷载增加，部分反力向中间转移，基底中心处的土压力迅速增大，最终形成如图11所示的土压力分布.

图10基底土压力随时间变化曲线(加载速率1.75 mm·s-1)

Fig.10Evolution of basal pressure (loading rate 1.75 mm·s-1)

图11　不同时刻基底土压力分布图

Fig.11Distribution of soil pressure in basal surface at different times

3　结语

本研究设计加工了一套可以进行位移速率控制的载荷模型试验加载装置和不同尺寸的载荷板.用4种尺寸圆盘的载荷板在模型箱中进行位移速率控制的载荷试验.对比分析了位移加载速率和载荷板尺寸对TJ-1模拟月壤地基极限承载力的影响.得出如下主要结论：

(1) 使用设计加工的可进行位移速率控制加载装置的载荷试验结果表明，大多数加载试验结果具有良好的重复性，因此可在模型箱中较好地进行载荷试验.

(2) 在位移速率控制时，同一载荷板条件下，TJ-1模拟月壤的地基极限承载力随着加载速率的增加而增加；整体来说，相同加载速率下，TJ-1模拟月壤地基极限承载力随着载荷板尺寸的增加而增加.

(3) 在位移速率控制时，加载速率和基础尺寸均会对地基弹性模量产生影响.在相同载荷板条件下，TJ-1模拟月壤的地基变形模量随着加载速率的增加而增加；在相同加载速率下，TJ-1模拟月壤的地基变形模量随着载荷板尺寸的增加而增加.

(4) 加载初期，各点土压力增加较快，特别是中心点.加载试验时，直径12 cm圆盘载荷板的底面中心点土压力最大，而距中心39 mm处的土压力值比距中心26 mm处的土压力值略大.

月面环境与地面环境差距较大(低重力场、高真空、高温差等)，后续将研究月面环境对模拟月壤承载力的影响，以由地面环境下的试验结果推得月球上真实月壤土的承载特性.

[1]欧阳自远. 我国月球探测的总体科学目标与发展战略[J]. 地球科学进展, 2004, 19(3): 351.

OUYANG Ziyuan. Scientific objectives of Chinese lunar exploration project and development strategy[J]. Advance in Earth Sciences, 2004, 19(3):351.

[2]Benaroya H, Bernold L, Chua K M. Engineering, design and construction of lunar bases[J]. Journal of Aerospace Engineering, 2002, 15(2): 33.

[3]于登云, 葛之江, 王乃东, 等. 月球基地结构形式设想[J]. 宇航学报, 2012, 33(12): 1840.

YU Dengyun, GE Zhijiang, WANG Naidong,etal. Supposal for structure form of lunar base[J]. Journal of Astronautics, 2012, 33(12): 1840.

[4]欧阳自远. 月球科学概论[M]. 北京：中国宇航出版社, 2005.

OUYANG Ziyuan. Introduction to lunar science [M]. Beijing: China Astronautic Publishing House, 2005.

[5]郑永春, 欧阳自远, 王世杰, 等. 月壤的物理和机械性质[J]. 矿物岩石, 2005, 24(4): 14.

ZHENG Yongchun, OUYANG Ziyuan, WANG Shijie,etal. Physical and mechanical properties of lunar regolith[J]. Journal of Mineralogy and Petrology, 2005, 24(4):14.

[6]Perko H, Nelson J, Sadeh W. Surface cleanliness effect on lunar soil shear strength[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 27(4): 371.

[7]Chang C S, Hicher P Y. Model for granular materials with surface energy forces[J]. Journal of Aerospace Engineering, 2009, 22(1): 43.

[8]Kobayashi T, Ochiai H, Yasufuku N,etal. Load-settlement characteristics of Japanese lunar soil simulant in partial gravity[C]∥Space resources roundtable VIII: Program and abstracts. Golden:[s.n.], 2007:37-38.

[9]Kobayashi T, Ochiai H, Suyama Y,etal. Bearing capacity of shallow foundations in a low gravity environment[J]. Soils and Foundations, 2009, 49(1): 115.

[10]Bui H H, Kobayashi T, Fukagawa R,etal. Numerical and experimental studies of gravity effect on the mechanism of lunar excavations [J]. Journal of Terramechanics, 2009, 46(3): 115.

[11]Perkins S W, Madson C R. Mechanical and load-settlement characteristics of two lunar soil simulants [J]. Journal of Aerospace Engineering, 1996, 9(1): 1.

[12]蒋明镜, 戴永生, 张熇, 等. TJ-1模拟月壤承载特性的现场试验研究[J]. 岩土力学, 2013, 34(6): 1529.

JIANG Mingjing, DAI Yongsheng, ZHANG He,etal. Field experimental research on bearing properties of TJ-1 lunar soil simulant[J]. Soil and Rock Mechanics, 2013, 34(6): 1529.

[13]邹猛, 李建桥, 何玲, 等. 不同粒径分布模拟月壤承压特性试验研究[J]. 航空学报, 2012, 33(12): 2338.

ZOU Meng, LI Jianqiao, HE Ling,etal. Experimental study on the pressure-sinkage characteristic of the simulant lunar regolith with different particle size distributions[J]. Journal of Astronautics, 2012, 33(12): 2338.

[14]Arslan H, Batiste S, Sture S. Engineering properties of lunar soil simulant JSC-1A[J]. Journal of Aerospace Engineering, 2009, 23(1): 70.

[15]Batiste S N, Lankton M R. Lunar regolith geotechnical properties: Implications for exploration[C]∥Earth & space. League City: ASCE, 2006: 1-7.

[16]Klosky J L, Sture S, Ko H Y,etal. Geotechnical behavior of JSC-1 lunar soil simulant[J]. Journal of Aerospace Engineering, 2000, 13(4): 133.

[17]Jiang M J, Li L Q, Sun Y G. Properties of TJ-1 lunar soil simulant[J]. Journal of Aerospace Engineering, 2011, 25(3): 463.

[18]蒋明镜, 李立青, 刘芳, 等. 含水率和颗粒级配对TJ-1模拟月壤力学性能影响的试验研究[J].岩土力学, 2011, 32(7): 21.

JIANG Mingjing, LI Liqing, LIU Fang,etal. Effects of principal stress direction and deviatoric stress ratio on deformation behavior of TJ-1 lunar soil simulant[J]. Soil and Rock Mechanics, 2011, 32(7): 21.

[19]蒋明镜, 王新新. 不同贯入倾角下TJ-1模拟月壤静力触探模型箱试验研究[J]. 岩土工程学报, 2013, 35(8): 1442.

JIANG Mingjing, WANG Xinxin. Investigation of TJ-1 lunar soil simulant cone penetration tests by calibration chamber under different penetration angles[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1442.

Experimental Study of Bearing Behavior of TJ-1 Lunar Soil Simulant Using Physical Model

JIANG Mingjing1, XI Banglu1, SUN Dean2, WANG Chuang3

(1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2. Department of Civil Engineering, Shanghai University, Shanghai 200072, China; 3. China Academy of Space Technology, Beijing 100094, China)

The engineering properties of lunar regolith can be studied with the aid of the modern experimental technology, which is a practicable method to solve the problem of geotechnical engineering on the moon. The indoor physical model loading test is of great significance in studying soil bearing capacity. In this paper, the loading device with the loading rate controlled was designed. Then, indoor model loading tests were conducted on TJ-1 lunar regolith simulant by using the circular loading plates with four different sizes. The results show that using the same loading plate, the ultimate bearing capacity and deformation modulus of TJ-1 lunar regolith simulant increase with the loading rate. Using the same loading rate, the ultimate bearing capacity and deformation modulus of TJ-1 lunar soil simulant increase with the loading plate size. In addition, the basal soil pressure at the center is the largest during loading.

bearing capacity; TJ-1 lunar soil stimulant; plate loading test; loading rate effect; loading plate size effect

2015-01-16

国家杰出青年科学基金(51025931);国家自然科学基金(51179128)

蒋明镜(1965—)，男，教授，博士生导师，博士后，主要研究方向为天然结构性黏土、砂土、太空土、深海能源土、非饱和土的宏微观之试验、本构模型和数值分析以及土体逐渐破坏分析等.E-mail:mingjingjiang@tongji.edu.cn

TU43

A