T形钢管混凝土单向偏压长柱力学性能分析
雷 敏, 沈祖炎, 李元齐, 罗金辉
(1. 西南交通大学 土木工程学院, 四川 成都 610031; 2. 同济大学 土木工程学院, 上海 200092;3. 同济大学 土木工程国家防灾减灾重点实验室, 上海 200092)
T形钢管混凝土单向偏压长柱力学性能分析
雷敏1,2, 沈祖炎2,3, 李元齐2,3, 罗金辉2
(1. 西南交通大学 土木工程学院, 四川 成都 610031; 2. 同济大学 土木工程学院, 上海 200092;3. 同济大学 土木工程国家防灾减灾重点实验室, 上海 200092)
采用普通T形钢管混凝土柱的核心混凝土等效单轴本构关系,利用纤维模型程序对T形钢管混凝土单向压弯长柱的力学性能进行分析,讨论了混凝土抗压强度、钢材屈服强度、管壁宽厚比、截面肢宽厚比、加载角度、长细比和轴压比等参数对构件偏压稳定承载力的影响.研究表明:混凝土工作承担系数、加载角度和长细比对正则化的轴力与弯矩相关曲线的形状有重要影响;基于大量数值结果回归分析,提出了T形钢管混凝土柱单向压弯承载力的简化计算方法,简化方法计算结果与纤维模型分析结果、试验结果吻合良好,简化方法可为工程设计提供参考.归
T形钢管混凝土柱; 单向偏压; 承载能力; 相关方程
异形钢管混凝土柱具有钢管混凝土柱承载能力高、抗震性能优越、施工方便、耐火性能好等优点,同时又有钢筋混凝土异形柱结构满足室内空间美学要求、可持续化、人性化的优点,在未来的小高层建筑中有着广阔的应用前景.近年来国内研究者对异形钢管混凝土柱力学性能的研究予以了广泛的关注,主要侧重于轴压短柱、偏压短柱的静力性能研究[1-3]、构件的抗震性能研究[4-5],以及采用不同的加劲措施来改善异形钢管混凝土柱的延性和承载力[6-9].实际工程中,构件以中长柱居多,同时完善冷成型工艺可使异形钢管一次成型,方便施工,减小异形钢管因为焊接和弯折加工的生产成本.因此本文在对普通构造T形钢管混凝土柱(其截面如图1所示)轴压、偏压试验研究,轴压截面强度、轴压稳定及压弯构件截面强度分析研究[10]的基础上,进一步采用纤维模型程序对T形钢管混凝土单向压弯中长柱的力学性能进行了分析,讨论了混凝土抗压强度、钢材屈服强度、管壁宽厚比、截面肢宽厚比、加载角度以及长细比等参数对该类组合柱承载性能的影响;基于大量数值结果回归分析,提出了T形钢管混凝土柱单向压弯承载力的简化计算方法,简化方法计算结果与纤维模型分析结果、试验结果吻合良好,简化计算方法可为工程设计提供参考.
1 纤维模型
本文采用纤维模型程序对T形钢管混凝土单向压弯构件的力学性能进行分析,纤维模型的基本假定、建立过程和材料本构等见参考文献[10],构件加载方向、单元划分如图1所示.

a 荷载用点及应变分布

b 钢管单元划分

c 混凝土单元划分
图1荷载作用位置及截面单元划分
Fig.1Location of loading and fiber elements of the section
2 参数分析
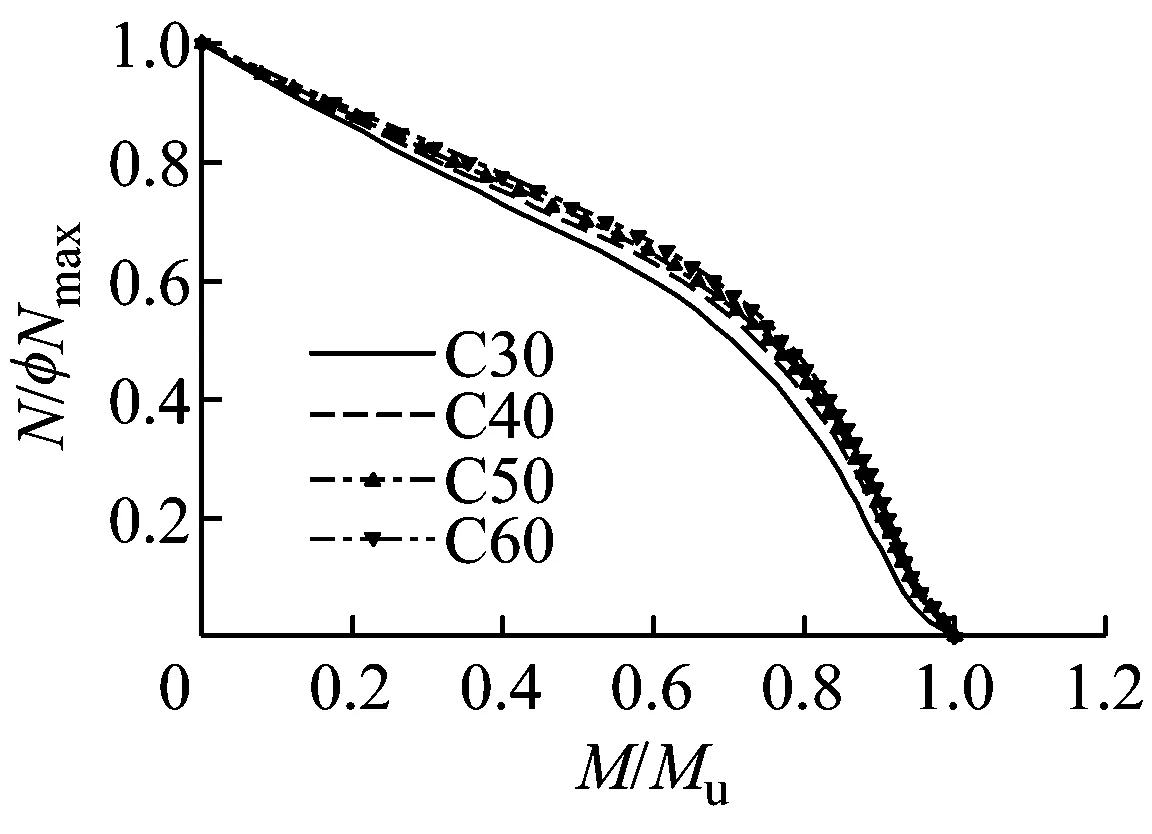
对于T形钢管混凝土压弯构件,影响其偏压承载力的主要参数有:混凝土抗压强度、钢材屈服强度、钢管管壁厚度(反映管壁宽厚比)、加载角度、截面肢宽厚比和构件长细比.本文对截面肢宽B和肢高H为250, 300, 400 mm,肢厚hf和bw均为100 mm的T形钢管混凝土柱进行了参数分析.参数包括:混凝土强度等级为C30—C60;钢材屈服强度fy为235~390 MPa;管壁厚度t为6~10 mm;截面肢宽厚比B/hf为2.5~4.0;加载角度为-90°,0°,+90°;长细比λ为0~100.构件的基本参数为:B=H=300 mm,hf=bw=100 mm,t=8 mm, 混凝土强度等级为C40,钢材屈服强度fy为345 MPa,长细比λx为40,加载角度为+90°.不同参数对构件的偏压稳定承载力N/φNmax-M/Mu相关曲线的影响如图2所示,其中N和M为构件所能承担的轴力和弯矩,φNmax和Mu为构件的轴压稳定承载力和纯弯承载力.
2.1混凝土抗压强度的影响
从图2a可以看出:对加载角度为+90°,长细比λx为40的T形钢管混凝土柱,其稳定承载力N/φNmax-M/Mu相关曲线与截面的强度N/Nmax-M/Mu相关曲线[10]类似.随着混凝土强度的提高(C30—C60),混凝土承担荷载的比例(混凝土工作承担系数αc=fcAc/(fcAc+fyAs))增大,轴压稳定承载力φNmax及构件纯弯承载力Mu均增大,但Mu增加很小.由于忽略混凝土的抗拉强度,构件截面上的拉力分量由钢管承担,混凝土对抗弯承载力M的贡献相对小于对轴向承载力N的贡献.因此混凝土工作承担系数αc的增加,对压弯状态下抗弯承载力的提高幅度大于对构件纯弯承载力的提高幅度,使得构件的稳定承载力相关曲线度N/φNmax-M/Mu逐渐外凸,曲线形状与钢筋混凝土柱的相关曲线相似.2.2钢材屈服强度的影响
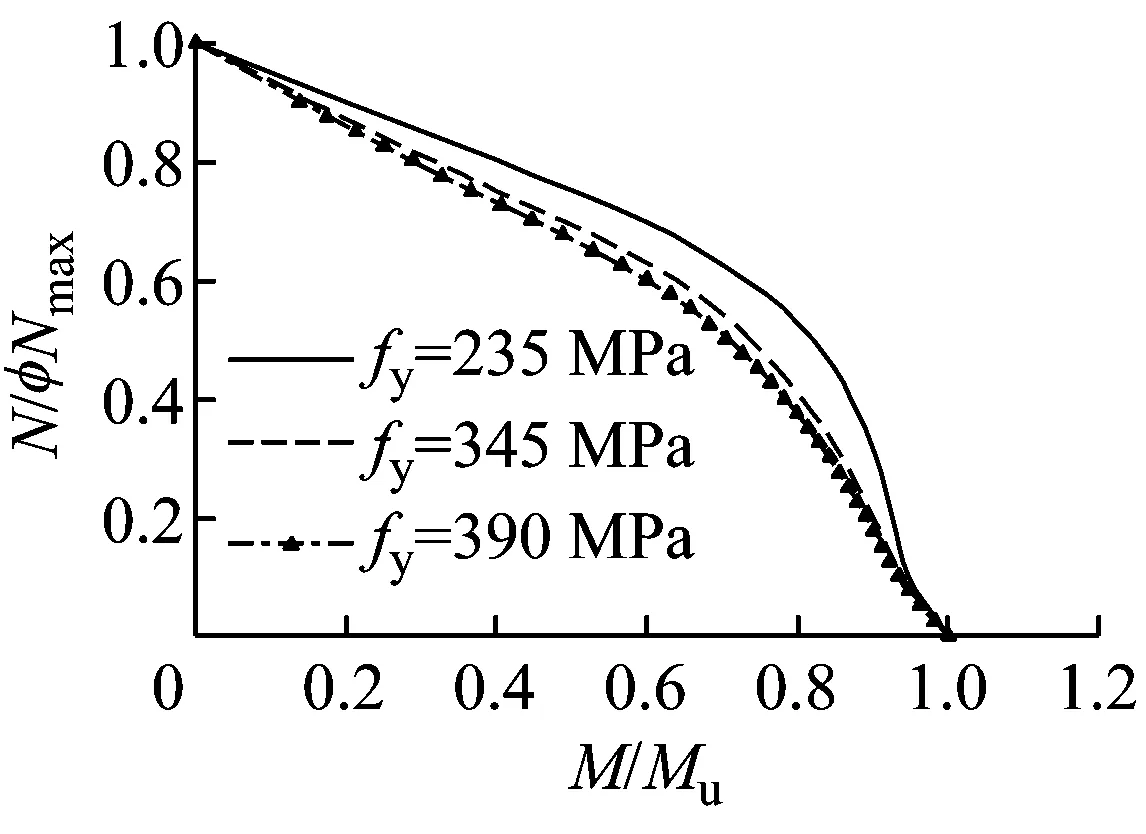
从图2b可以看出:对加载角度为+90°,长细比λx为40的T形钢管混凝土柱,其稳定承载力N/φNmax-M/Mu相关曲线与截面的强度N/Nmax-M/Mu相关曲线[10]类似.随着钢材屈服强度(235~390 MPa)的提高,混凝土工作承担系数αc降低,钢管承担的荷载比例增大,构件的轴压稳定承载力φNmax及构件的纯弯承载力Mu均增大.由于忽略混凝土的抗拉强度,拉力分量由钢管抵抗,钢管对抗弯承载力的贡献大于对轴向承载力的贡献.所以钢管承担荷载的比例1-αc增大,对压弯状态下抗弯承载力M的提高幅度小于构件纯弯承载力的提高幅度,因此构件稳定承载力N/φNmax-M/Mu相关曲线逐渐向内靠拢,与钢柱的相关曲线相似.
a 混凝土强度
b 钢材强度
c 管壁厚度
d 截面肢宽厚比
e 加载角度
-90°加载
0°加载

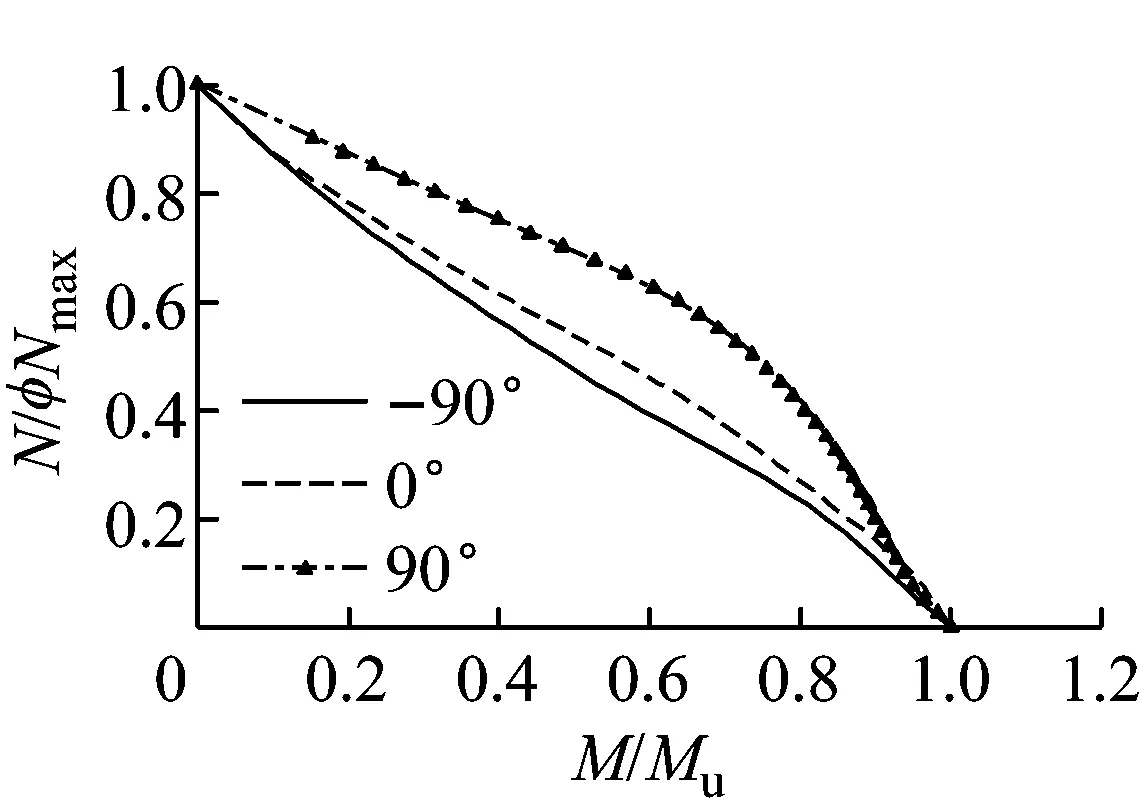
+90°加载 f 长细比图2 不同参数对N/φNmaxM/Mu相关曲线的影响Fig.2 Effects of different parameters on N/φNmaxM/Mu interaction
2.3管壁宽厚比的影响
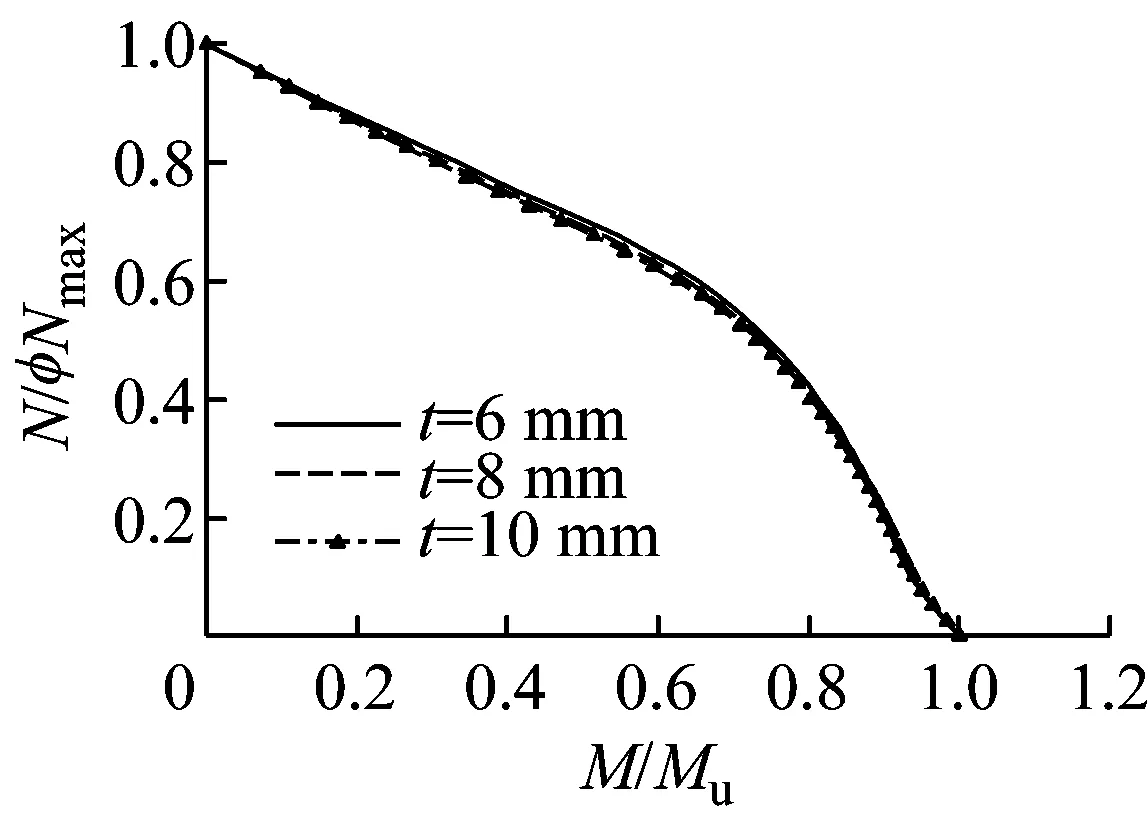
从图2c可以看出:对加载角度为+90°,长细比λx为40的T形钢管混凝土柱,随着管壁厚度(6,8,10 mm)的增加、管壁宽厚比(50.0,37.5,30.0)的减小,混凝土工作承担系数降低,其对构件稳定承载力N/φNmax-M/Mu相关曲线形状的影响与钢材屈服强度的增加类似,曲线逐渐向内靠拢,但管壁宽厚比的变化对相关曲线形状的影响不明显.
2.4截面肢宽厚比的影响
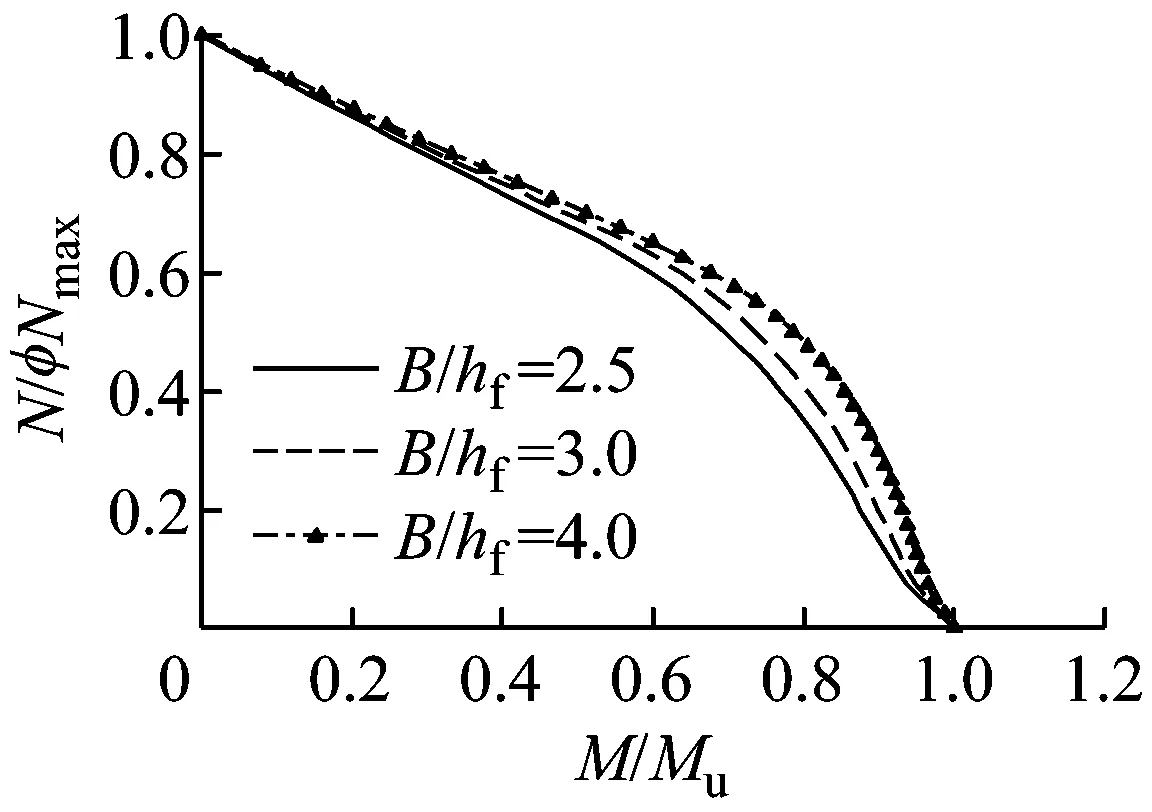
从图2d可以看出:对加载角度为+90°,长细比λx为40,截面肢厚为100 mm的T形钢管混凝土柱,当截面肢宽厚比由图中的2.5升到4.0时,混凝土工作承担系数(分别为0.313, 0.277, 0.221)依次减小,但相关曲线越来越向外突出,这主要是因为对于不同肢宽厚比的T形钢管混凝土柱截面,尽管混凝土工作承担系数变小了,但实际受压区的混凝土面积率却增大了,混凝土参于实际工作的比例增加,从而相关曲线越来越外凸.
2.5加载角度的影响
从图2e可以看出,对长细比λx为40的T形钢管混凝土柱,随着加载角度从-90°向+90°变化, 构件的稳定承载力N/φNmax-M/Mu相关曲线的形状差异较大.这与T形钢管混凝土的截面特性及力学性能有关,即随着角度的变化,同一截面相同长度构件在不同方向的长细比不相同,同时又由于忽略混凝土的抗拉强度,混凝土受压参与截面承载贡献的比重也有差别.从而导致相关曲线的形状差异较大.
2.6长细比的影响
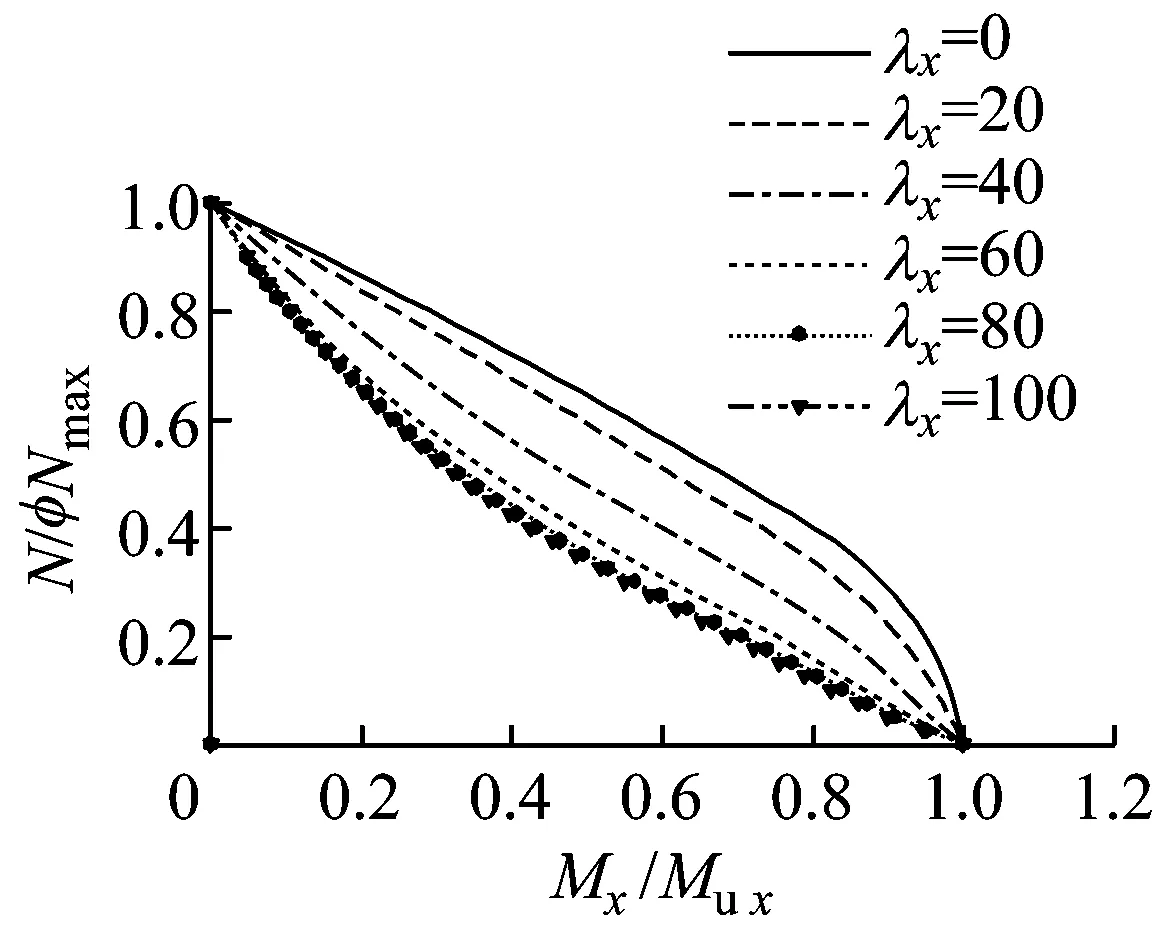
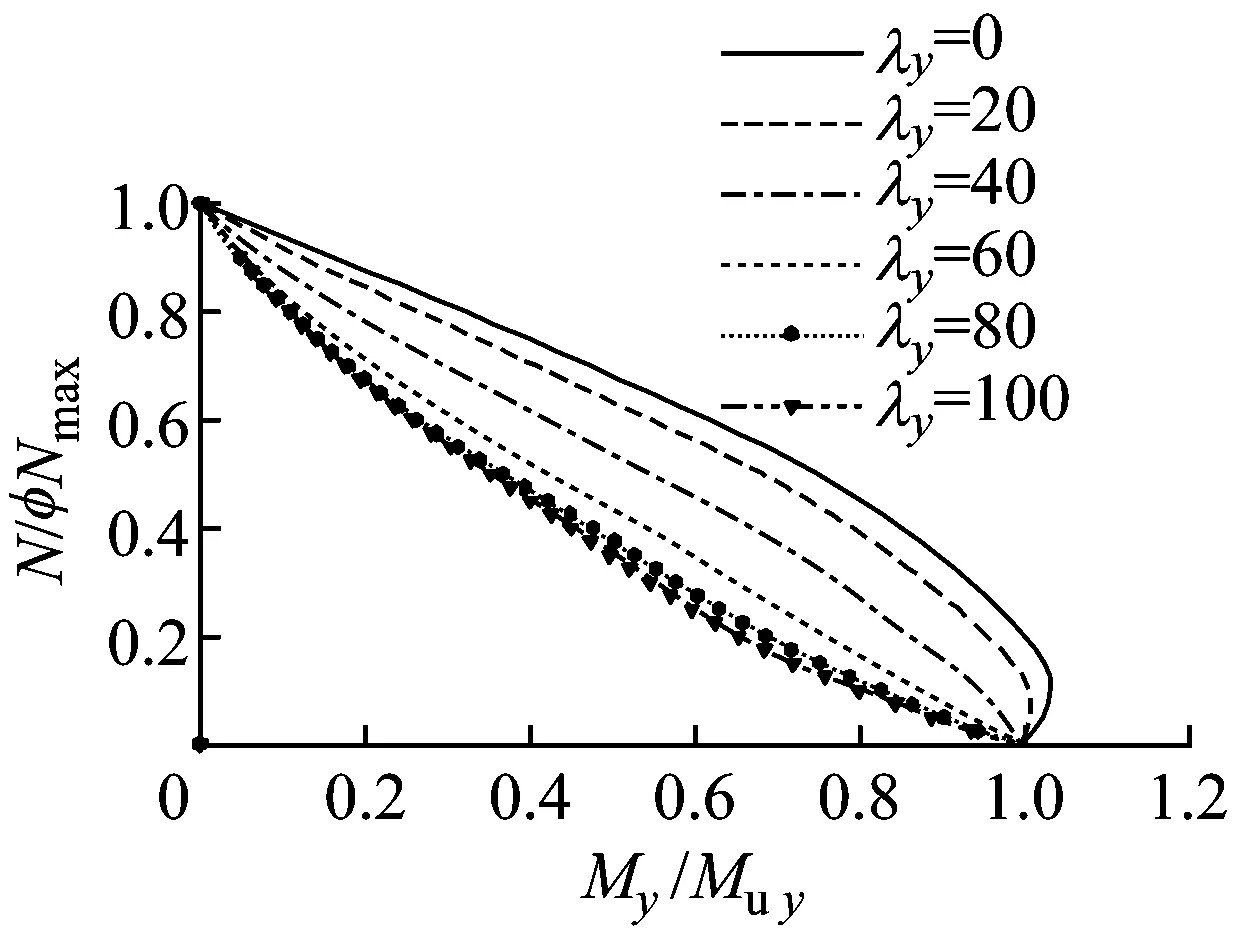
从图2f和图3可以看出,无论是-90°,0°,还是+90°加载,长细比对构件的稳定承载力N/φNmax-M/Mu相关曲线的形状影响均为显著.随着构件长细比的增大,二阶效应对构件轴向承载力和抗弯承载力影响显著,其压弯承载力逐渐减小,承载力相关曲线由向外凸的曲线逐渐变化为向内凹的曲线.
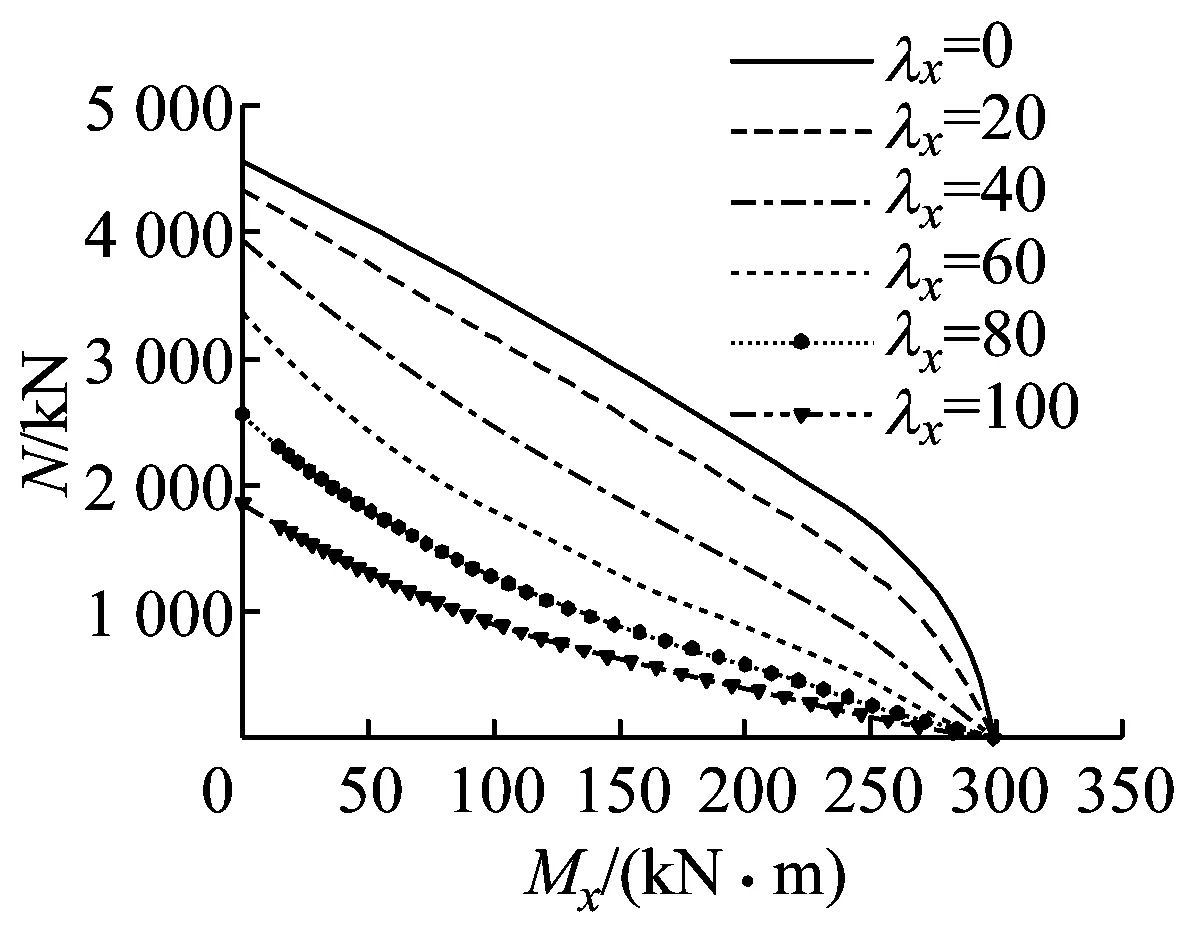
a -90°加载
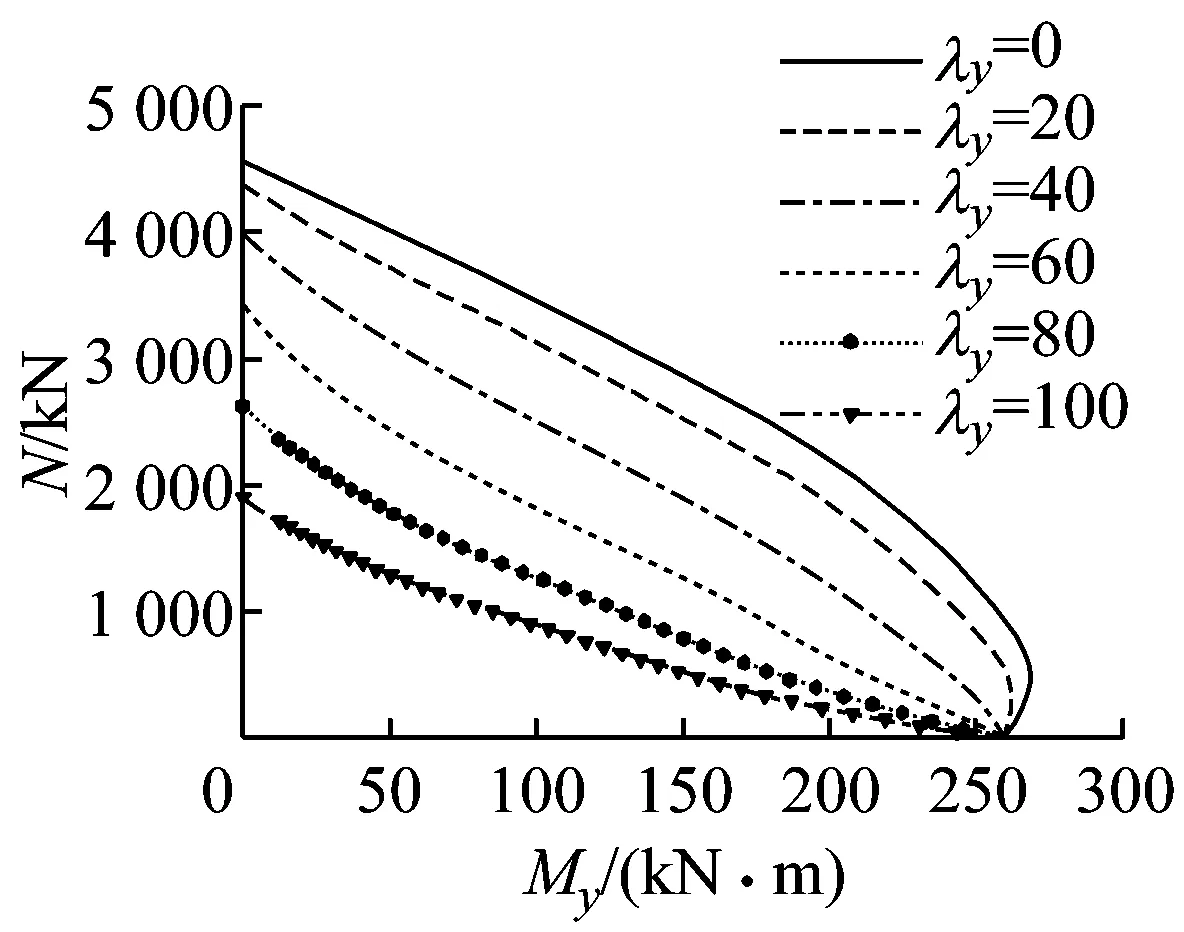
b 0°加载
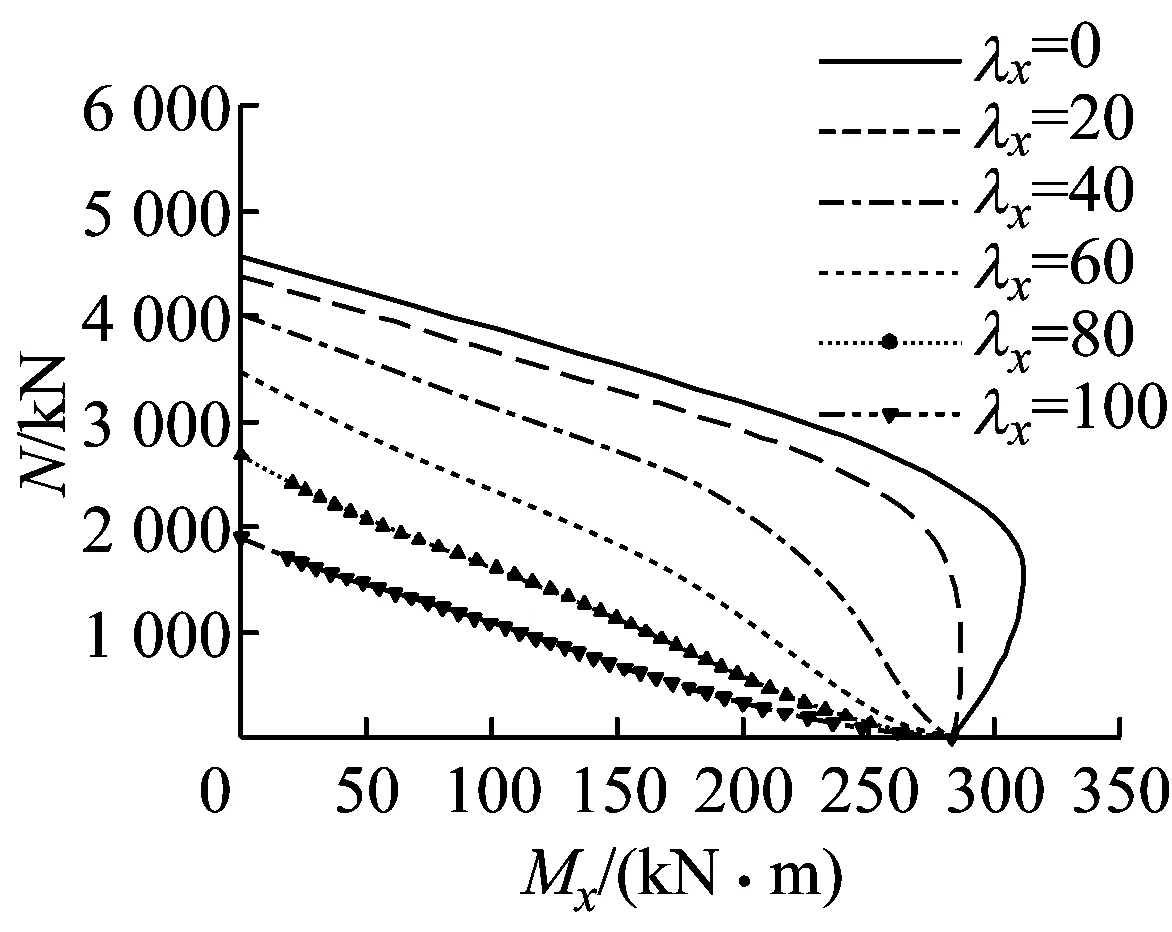
c +90°加载图3 长细比对N-M相关曲线的影响Fig.3 Effects of slenderness ratio on N -M interaction
2.7轴压比的影响
从图2和图3可以看出,随着轴压比n(n=N/Nmax,轴力比n1=N/φNmax可间接反映轴压比n)的降低,构件的抗弯承载力通常增大,但也有部分构件的抗弯承载力在轴压比降低到一定程度后反而减小,这与构件的混凝土工作承担系数、加载角度、长细比等因素有关.
3 构件单向偏压承载力简化计算公式
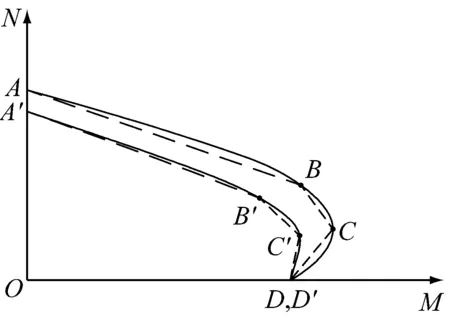
在T形钢管混凝土柱截面单向压弯强度相关曲线AB,BC,CD三折线简化表达的基础上[10](图4),本文考虑长细比对承载力的影响,经参数分析,采用如下三段式(A′B′,B′C′,C′D′)曲线来表达T形钢管混凝土柱单向压弯稳定承载力相关方程[11-12]:
a N-M曲线

b N/Nu-M/Mu图4 简化的相关曲线Fig.4 Simplified interaction for CFTST columns
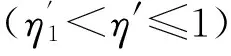
(1)
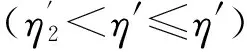

(2)
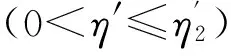
(3)
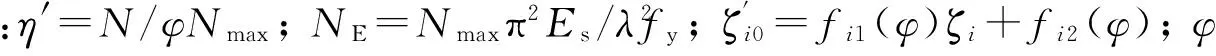
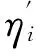
构件稳定承载力的特征点B′,C′的横坐标
(4)
式中:fi1(φ)=ai1φ2+ai2φ+1-ai1-ai2;fi2(φ)=bi1φ2+bi2φ-bi1-bi2;ζi为T形钢管混凝土柱截面强度相关曲线特征点B,C的横坐标(ζi=Mi/Mu,Mu为只产生单向弯矩时的纯弯强度),见文献[10]; 参数aij,bij取值见表1.
图5给出了不同加载角度时,不同长细比情况下简化计算公式计算结果与数值计算结果的对比.从图中可以看出,本文简化公式的计算结果与数值计算结果吻合较好.
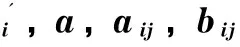
表1 不同方向加载时构件参数取值Tab.
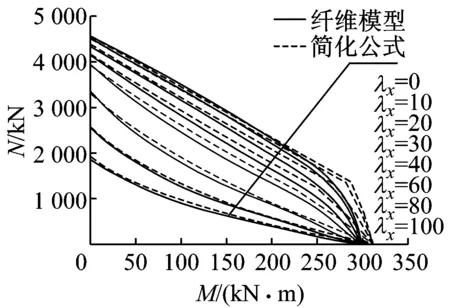
a -90°加载
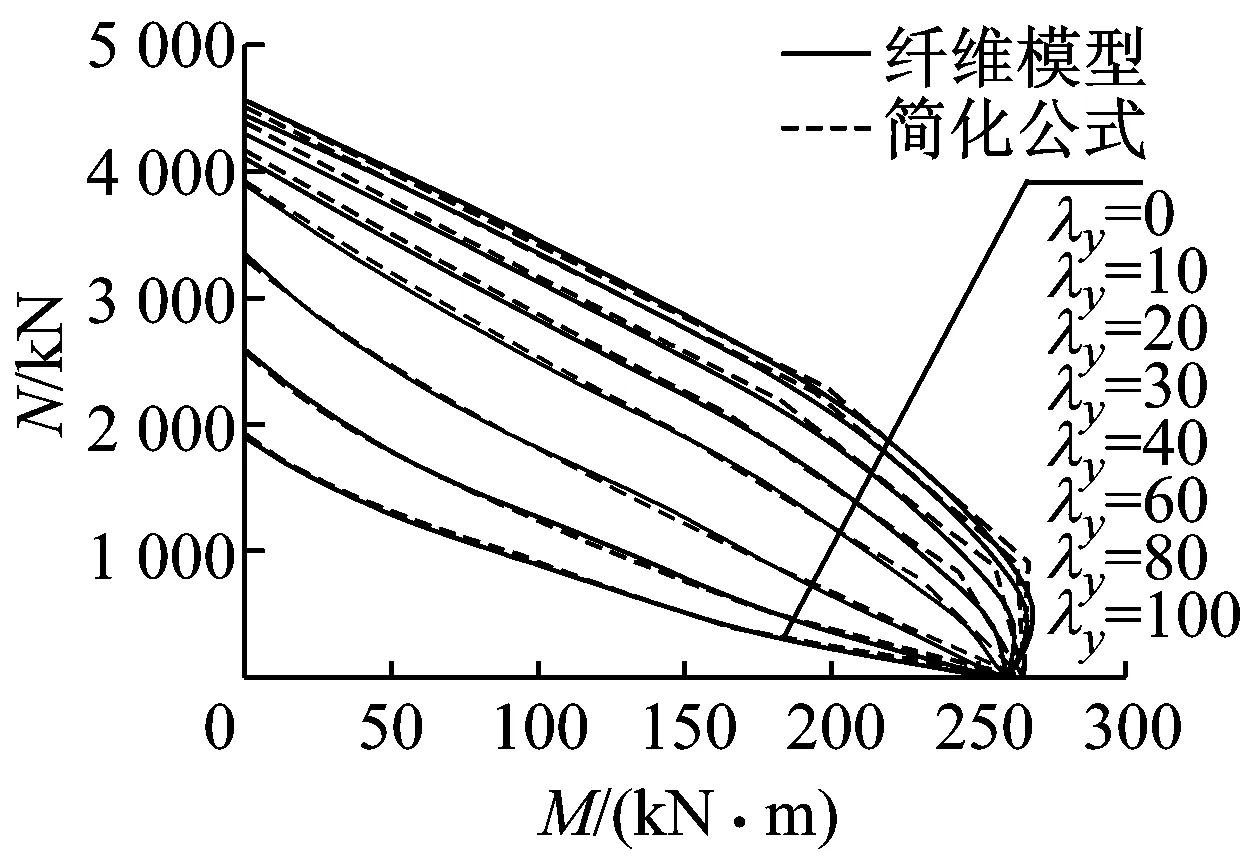
b 0°加载

c 90°加载图5 简化公式与纤维模型计算结果比较Fig.5 Comparison of interaction predicted by simplified formula and fiber element analysis
图6给出了简化计算公式计算结果与数值计算结果与文献[10]试验结果的对比.图中T3005-2200/0/-50等为文献[10]中的试件编号.从图中可以看出,本文的简化公式、纤维模型程序的计算结果与试验值吻合良好.

a T3005-2200/0/-50:-90°加载
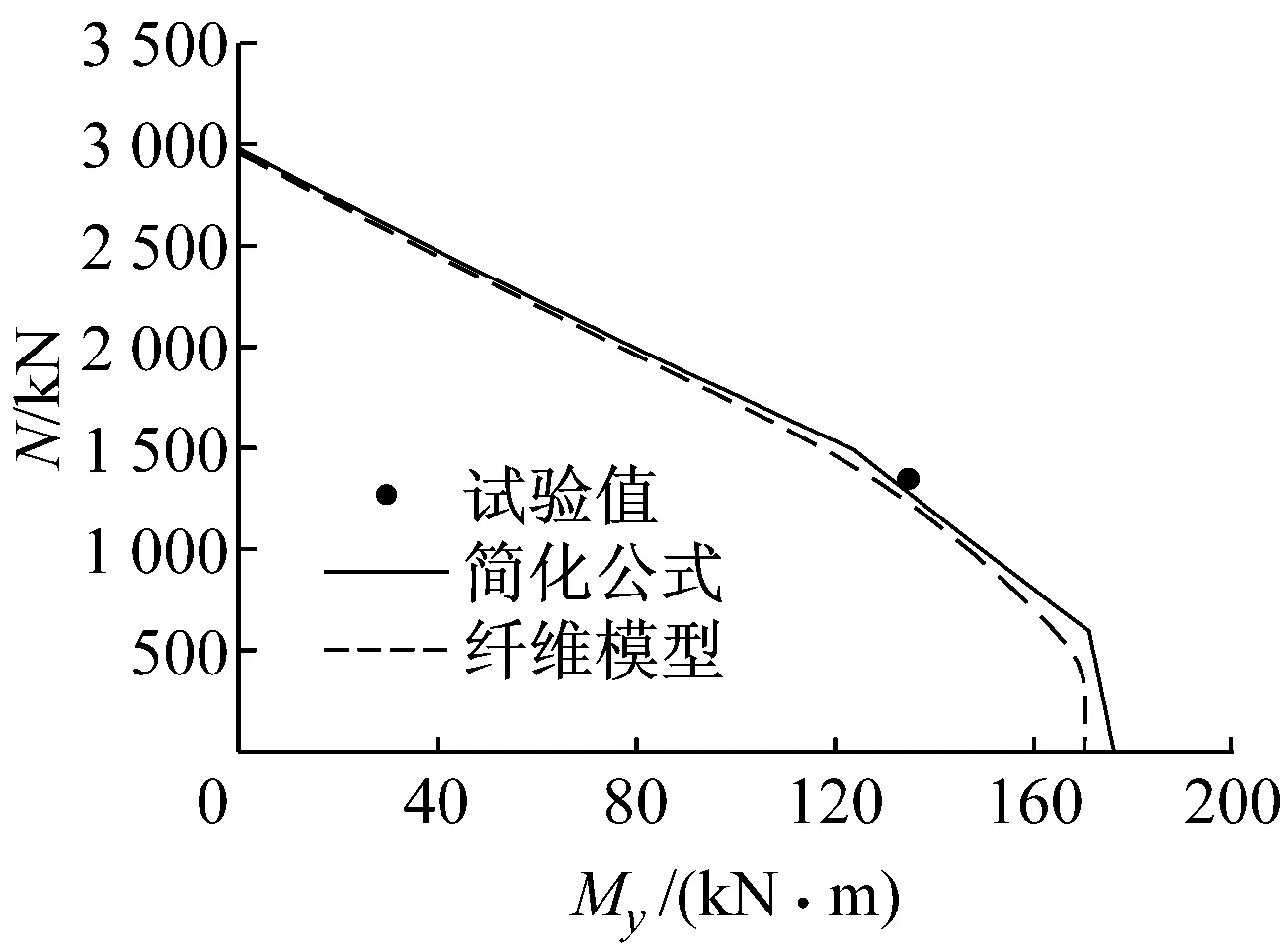
b T3005-2600/100/0: 0°加载
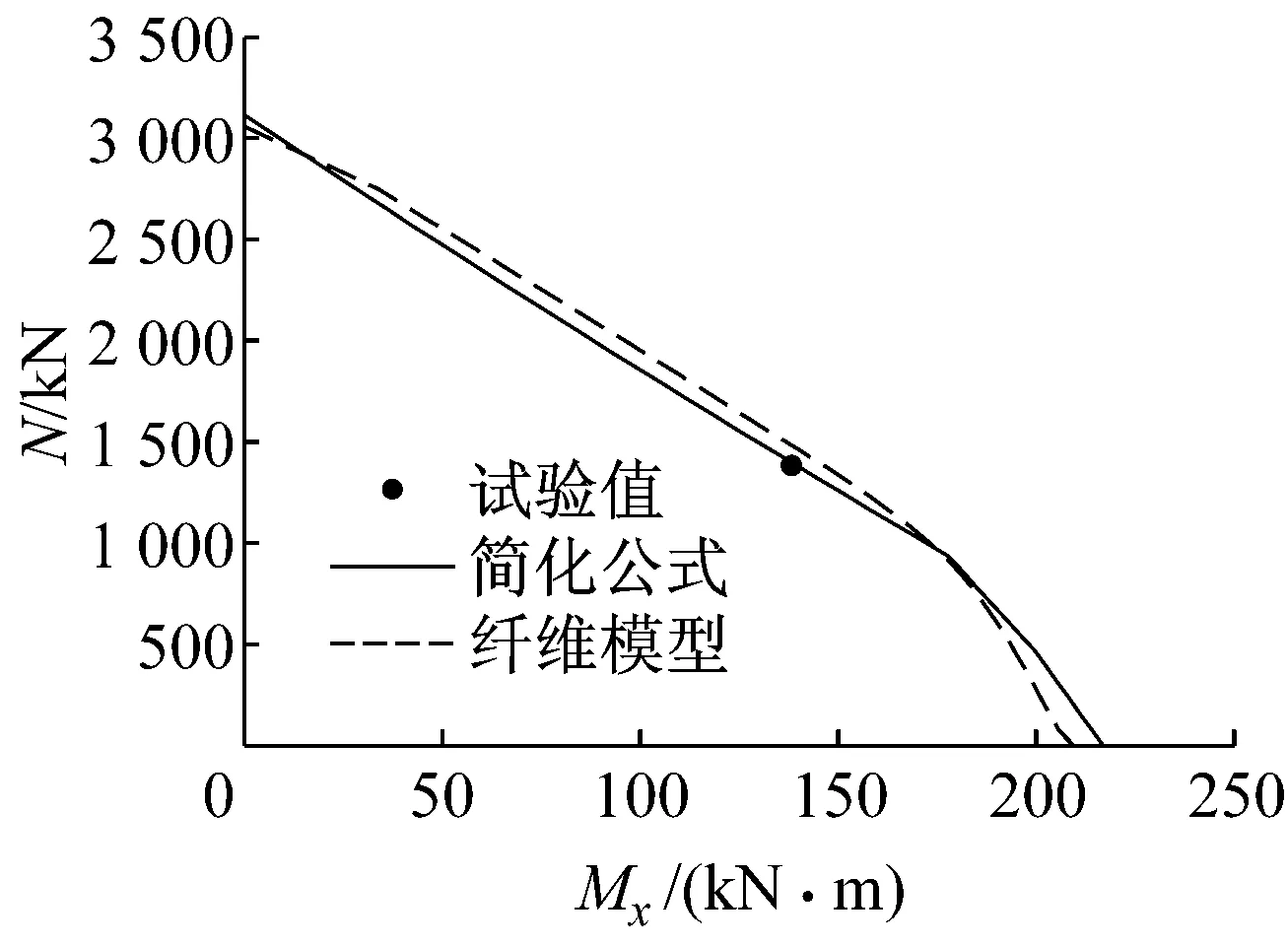
c T3006-2600/0/-100:-90°加载
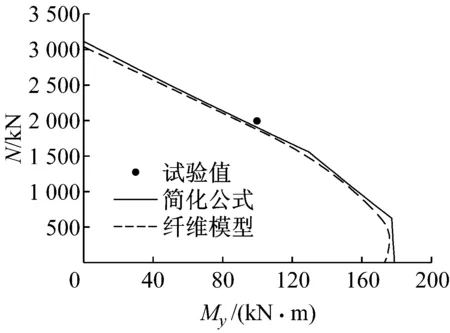
d T3006-2200/50/0: 0°加载图6 简化公式、纤维模型计算结果与试验值比较Fig.6 Comparison of results predicted by simplified formula, fiber element analysis and from experiment
4 结论
(1)对T形钢管混凝土柱偏压稳定承载力N/φNmax-M/Mu相关曲线参数分析表明:混凝土强度越高,相关曲线越向外凸出,与钢筋混凝土柱的相关曲线越相似;钢材强度越高以及管壁厚度越厚,相关曲线越向内收拢,曲线与钢柱的相关曲线更相似;截面肢宽厚比的变化会引起混凝土参与实际工作的比例变化,从而影响相关曲线的形状.
(2)随着加载角度从-90°向0°,再向+90°变化,由于同一截面相同长度构件在不同方向的长细比不相同,以及混凝土受压参与截面承载贡献的比重的差别,构件的稳定承载力N/φNmax-M/Mu相关曲线的形状差异较大.
(3)长细比对构件的稳定承载力N/φNmax-M/Mu相关曲线的形状影响显著.无论是-90°,0°还是+90°加载,随着构件长细比的增大,承载力相关曲线由向外凸的曲线逐渐往向内凹的曲线过渡.-90°,0°,+90°三个不同方向上加载时,稳定承载力N/φNmax-M/Mu相关曲线形状差异较大.
(4)提出了T形钢管混凝土单向偏压柱的稳定承载力N/φNmax-M/Mu相关关系的简化计算方法;简化方法的计算结果与数值分析结果、试验值吻合良好,简化公式能有效计算T形钢管混凝土单向偏压柱的承载力,可为工程设计提供参考.
[1]Chen Z Y, Shen Z Y. Behavior of L-shaped concrete-filled steel stub columns under axial loading: Experiment [J]. Advanced Steel Construction, 2010, 6(2): 688.
[2]林震宇. L形钢管混凝土构件力学性能若干关键问题研究[D]. 上海:同济大学,2009.
LIN Zhenyu. Study on some key problem on behavior of L-shaped concrete-filled steel tubular columns [D].Shanghai: Tongji University, 2009.
[3]左志亮, 蔡健, 刘明峰,等. 带约束拉杆T形钢管混凝土短柱偏压试验研究[J]. 建筑结构学报, 2011, 32(8): 79.
ZUO Zhiliang, CAI Jian, LIU Mingfeng,etal. Experimental study of T-shaped CFT stub columns with binding bars subjected to eccentric load [J]. Journal of Building Structures, 2011, 32(8): 79.
[4]王丹, 吕西林. T形、L形钢管混凝土柱抗震性能试验研究[J]. 建筑结构学报, 2005, 26(4):39.
WANG Dan, LÜ Xilin. Experimental study on seismic behavior of concrete-filled steel T-section, L-section columns[J]. Journal of Building Structures, 2005, 26(4):39.
[5]Shen Z Y, Lei M, Li Y Q,etal. Experimental study on the seismic behavior of concrete-filled L-shaped steel tube columns [J]. Advances in Structural Engineering, 2013, 16(7):1235.
[6]Zuo Z L, Cai J, Yang C. Axial load behavior of L-shaped CFT stub columns with bind bars [J]. Engineering Structures, 2012, 37: 88.
[7]Yang Y L, Yang H, Zhang S M. compressive behavior of T-shaped concrete filled steel tubular columns [J]. International Journal of steel structures, 2010, 10(4): 419.
[8]徐礼华, 杜国锋, 温芳,等. 组合T形截面钢管混凝土柱正截面受压承载力试验研究[J]. 土木工程学报, 2009, 42(6):14.
XU Lihua, DU Guofeng, WEN Fang,etal. Experimental study on normal section compression bearing capacity of composite T-shaped concrete-filled steel tubular columns [J]. China Civil Engineering Journal, 2009, 42(6):14.
[9]屠永清, 刘林林, 叶英华. 多室式钢管混凝土T形中长柱轴压性能研究[J]. 土木工程学报, 2012, 45(9):27.
TU Yongqing, LIU Linlin, YE Yinghua. Study on the properties of multi-cell T-shaped concrete-filled steel tubular intermediate long columns under axial load [J]. China Civil Engineering Journal, 2012, 45(9):27.
[10]雷敏. T形钢管混凝土构件力学性能若干关键问题研究[D]. 上海:同济大学, 2014.
LEI Min. Study on some key problem on behavior of T-shaped concrete-filled steel tubular columns [D]. Shanghai: Tongji University, 2014.
[11]韩林海. 钢管混凝土结构——理论与实践[M]. 2版. 北京: 科学出版社, 2007.
HAN Linhai. Theory & practice of concrete-filled steel tubular structure [M]. 2nd ed. Beijing: Science Press, 2007.
[12]沈祖炎, 黄奎生. 矩形钢管混凝土柱偏心受力构件的设计方法[J]. 建筑结构, 2005, 35(1):5.
SHEN Zuyan, HUANG Kuisheng. Design method of eccentrically loaded members of concrete-filled rectangular steel tube [J]. Building Structure, 2005, 35(1):5.
Analysis of Behavior of Concrete-filled T-shaped Steel Tube Tall Column Subjected to Uniaxial Eccentric Load
LEI Min1,2, SHEN Zuyan2,3, LI Yuanqi2,3, LUO Jinhui2
(1. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. College of Civil Engineering, Tongji University, Shanghai 200092, China; 3. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)
In this paper, based on the equivalent uniaxial stress-strain relationship for concrete-filled T-shaped steel tube (CFTST) columns without stiffening measures, a fiber element model computing program was proposed for investigating the behavior of concrete-filled T-shaped steel tube slender columns, and the effects of different parameters on the behavior of CFTST columns under uniaxial eccentric load were investigated. The parameters in the analysis included the compressive strength of concrete, the yield strength of steel, the depth to thickness ratio of steel plate, the cross sectional depth to width ratio, the angle of the load, the slenderness ratio, and the axial load ratio. The results of theoretical analysis indicated that the normalized interaction curve of axial load versus bending moment was obviously influenced by the load ratio carried by core concrete, the load angle and the slenderness ratio. Based on the parametric analysis and regression analysis of a good many of numerical results, the simplified calculation methods were proposed to predict the load-carrying capacities of CFTST columns under uniaxial eccentric load. Good agreements between the values predicted by the simplified calculation methods, the fiber element model computing program and the experimental results were achieved, and the simplified calculation methods can be referred for practical engineering design.
concrete-filled T-shaped steel tube columns; uniaxial eccentric load; load-carrying capacity; interaction equation
2015-03-24
国家自然科学基金(51208375);中央高校基金科技创新项目(2682015CX081)
雷敏(1977—),男,讲师,工学博士,主要研究方向为组合结构. E-mail:leimin77@163.com
李元齐(1977—),男,教授,工学博士,主要研究方向为大跨结构抗风及冷弯型钢结构. E-mail:liyq@tongji.edu.cn
TU318.1; TU398.9
A

