基于模型参考方法的车辆非线性主动悬架反推控制

庞辉， 陈嘉楠， 梁军， 陈英

(西安理工大学 机械与精密仪器工程学院, 陕西 西安 710048)



基于模型参考方法的车辆非线性主动悬架反推控制

庞辉， 陈嘉楠， 梁军， 陈英

(西安理工大学 机械与精密仪器工程学院, 陕西 西安 710048)

针对车辆悬架系统存在的参数不确定性，提出一种基于模型参考控制的车辆非线性主动悬架反推控制器设计方法。建立悬架系统非线性模型，引入高低通滤波器，根据悬架动行程改变高低通滤波器的通频带宽，设计一种理想的模型参考系统。在此基础上，构造被控悬架系统与模型参考系统之间的车身位移和速度跟踪误差，基于反推控制方法和Lypaunov理论设计了误差跟踪反推控制器。通过仿真实验验证了所提出的误差跟踪反推控制器的有效性和跟踪精度。

兵器科学与技术； 非线性主动悬架； 反推控制； 跟踪误差； 模型参考控制

0　引言

近年来，车辆主动悬架控制理论与应用研究受到研究者和工程界的广泛关注。相较于被动悬架，主动悬架通过其作动器产生主动控制力来抑制由于路面不平引起的振动，但这会增加悬架动行程，而悬架动行程影响到整车总体布置和车辆性能，如何协调控制车身垂直加速度与悬架动行程之间的冲突成为一个难题。此外，悬架系统本身具有诸多非线性因素和不确定性，其控制优化问题成为研究热点[1-8]。

反推控制是一种针对控制对象变化和环境干扰影响而提出的控制策略，它采用反复选择合适的状态空间函数作为控制输入，通过迭代、反推和Lyapunov函数的优化，进而完成控制器设计[9-15]。文献[7]基于反推控制理论,将一种双自由度反推设计方法应用于交流伺服系统的位置控制,设计了一种位置控制器。文献[8]基于自适应积分反演控制方法，研究在未知海流作用下的水下航行器轴向运动跟踪控制问题，并取得良好的动态性能和对不确定项的鲁棒性，说明反演控制对解决这类非线性不确定系统的控制问题具有良好效果。在悬架系统研究中，文献[9]提出线性变参数 (LPV)的H∞控制方法与反推技术相结合的控制方法，该方法计算复杂, 且在参数快速转换时出现颤振现象。文献[10]同时引入一非线性高通滤波器和一非线性低通滤波器，设计一种车辆主动悬架的路面自适应控制器，但存在计算和模型复杂，实际工程中难以实现的缺点。文献[11]设计一种能够处理约束的自适应反推控制器，实现了半车主动悬架系统的多目标自适应反推控制，解决了系统不确定参数的问题。

本文基于反推控制理论，设计了一种理想的参考控制模型；然后基于模型参考方法和反推控制理论，定义车身位移和速度两个跟踪误差，并考虑不确定参数对悬架系统的影响，设计了一种误差跟踪反推控制器；最后对控制器性能进行仿真验证。

1　非线性主动悬架动力学模型

由于悬架系统中的某些机械元件在实际中是呈非线性变化的，采用线性模型描述通常与实际悬架系统相比具有一定简化误差。文献[16]中所建立的车辆悬架非线性模型分别引入了非线性弹簧模型和分段线性阻尼器模型，较好描述了悬架非线性特性，受此启发，本文建立非线性主动控制悬架系统模型如图1所示。

图1　非线性2自由度1/4主动悬架模型Fig.1　Nonlinear 2-DOF model of 1/4 active suspension

该悬架系统动力学方程为

(1)

式中：m1、m2分别为非簧载质量和簧载质量；zb、zw分别为车身和车轮位移；FS为悬架弹簧产生的力；FC为阻尼器阻力；kt为轮胎刚度；r为路面位移输入信号；u为主动控制力。具有一定刚度的非线性弹簧模型，其弹力随位移变化的曲线如图2所示，且遵循如下关系[16]：

FS=kn(Δy)+ks(Δy)3，

(2)

式中：kn为非线性弹簧刚度；ks为空间刚度系数；Δy=(zb-zw).

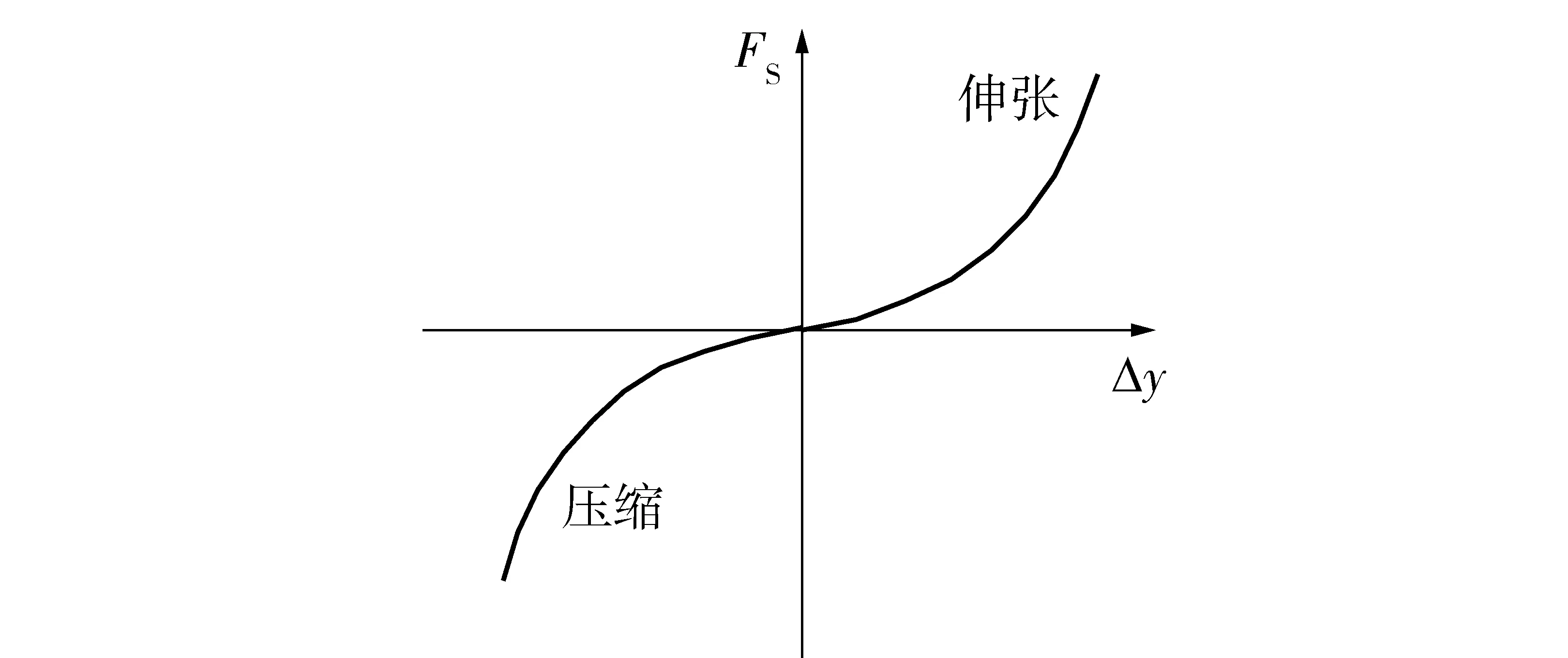
图2　非线性弹簧模型Fig.2　Nonlinear spring model

在压缩和伸张时具有不同阻尼率的分段线性阻尼器模型，其阻尼率随速度变化的曲线如图3所示，且遵循下列关系[16]：

(3)

(4)

图3　分段线性阻尼器模型Fig.3　Piecewise linear damper model

2　基于模型参考方法的误差跟踪反推控制器设计

基于模型参考方法的误差跟踪反推控制器设计分为两步，第1步是基于反推控制理论的模型参考系统设计，其目的是协调车身垂直加速度与悬架动行程之间的矛盾，使两个性能指标可以随路面激励的变化进行自适应调节，但此模型参考系统存在诸多不确定性参数，且模型结构复杂，实际工程中难以实现。为此，在第2步设计一种误差跟踪反推控制器，其控制基本原理是：在被控悬架与模型参考系统之间定义车身位移跟踪误差和速度跟踪误差，分别表示为ed、ev，在反推控制律的作用下，误差跟踪反推控制器可根据误差信号ed、ev对主动控制力u发出相应的控制信号，最终使跟踪误差ed、ev减小直至消失，即被控悬架输出接近于模型参考系统输出。图4为模型参考系统与误差跟踪反推控制器之间的控制原理结构图。

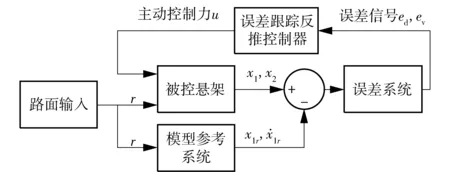
图4　控制原理结构图Fig.4　Control principle diagram

2.1模型参考系统设计

理想的模型参考系统可以对车身垂直加速度与悬架动行程进行协调控制，文献[17]通过引入一种非线性低通滤波器对主动悬架进行控制，其控制目标仅限于轮胎动位移，该方法难以适于不同路面激励的控制。通过仿真计算和分析，本文基于文献[17]做出改进，确定的两个控制目标为车身垂直加速度与悬架动行程，目标控制函数为

Jo=Whp(s)x1r+Wlp(s)(x1r-x3r)，

(5)

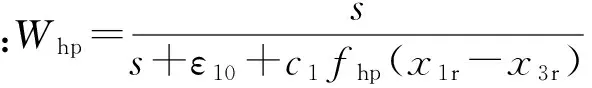
选择(4)式所描述的非线性悬架系统进行分析，此处状态变量x1、x2、x3、x4分别用x1r、x2r、x3r、x4r来表示，令ε1=ε10+c1fhp(x1r-x3r)，ε2=ε20+c2flp(x1r-x3r). 首先根据对车身加速度的控制要求，选择较小的ε10、ε20，然后依据悬架动行程大小调整ε1、ε2. 当悬架动行程变大时，使ε1、ε2增加，即能使滤波器Whp的通频带变窄，同时使Wlp的通频带加宽，使目标函数中悬架动行程所占比重增加，车身位移所占比重减小；反之，当悬架动行程减小时，使ε1、ε2减小，使目标函数中悬架动行程所占比重减小，车身位移所占比重增大。高低通滤波器Whp和Wlp中的非线性函数fhp(x1r-x3r)、flp(x1r-x3r)选取为

fhp(x1r-x3r)=

flp(x1r-x3r)=

(6)

式中：l1、l2、n1、n2均为正常数，并满足l1>n1.

下面进行模型参考系统控制律设计，为了获得良好的自适应性和鲁棒性，本模型参考系统采用反推设计方法，其控制律就是使目标控制函数Jo的绝对值尽可能减小。

1)定义Jo为第一个控制变量。令

y1=Whp(s)x1r,y2=Wlp(s)(x1r-x3r).

(7)

可得

(8)

综合(5)式、(7)式、(8)式可得

(9)

2)将x2r作为(9)式的虚拟控制输入，令x2r的理想值为

α=-d1Jo+ε1y1-ε2(x1r-x3r-y2)，

(10)

式中：d1为正常数。

一般情况下，系统运行时状态x2r的实际值与理想值之间存在误差，定义跟踪误差Jt为

Jt=x2r-α.

(11)

联立(9)式～(11)式得

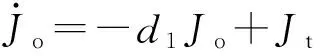
(12)

对(11)式求导得

(13)

(13)式出现了系统的实际控制输入u，设计其控制量为

(14)

式中：d2为正常数。将(14)式代入(13)式得

(15)

3)构造Lyapunov函数，假定

(16)

对(16)式求导并将(12)式、(15)式代入得

(17)

2.2误差跟踪反推控制器设计

为了简化模型参考系统，并考虑其中一些不确定或未知参数，进行误差跟踪反推控制器设计。根据(4)式，车身垂直运动的控制方程为

(18)

首先定义车身位移跟踪误差及其导数

(19)

式中：x1r为状态变量x1的一个理想期望值，则系统控制方程(18)式可重写为

(20)

以x2为虚拟控制量、ed作为被调节变量，基于Lyapunov稳定性理论，定义第一个正定无界的Lyapunov函数V1，并且当|ed|→∞时，V1(ed)→∞.

(21)

令x2的理想值为x2r，取

(22)

式中：c01为正常数。

则可得

(23)

系统运行时状态变量的实际值与理想值(模型参考系统)之间一般是存在误差的，这里定义车身速度跟踪误差为

ev=x2-x2r.

(24)

根据(19)式和(24)式，定义一个正定无界的Lyapunov函数V2为

(25)

由(25)式可得最终的主动控制力为

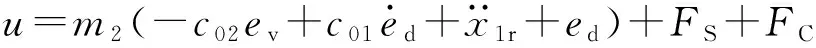
(26)

式中：c02为正常数。

基于Lyapunov理论对V2求导可得

(27)

将(26)式带入(27)式后可得

(28)

由(28)式可知，对于任意c01>0和c02>0，可使Lyapunov函数V2的导数是负定的，则系统满足Lyapunov稳定性条件,从而保证系统具有全局意义下的渐进稳定性。即通过控制律确保了跟踪误差变量ed、ev收敛，即当t→∞，ed→0,ev→0.

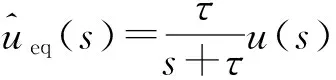
(29)

式中：τ是低通滤波器的截止频率，当该值足够大时可保证低频控制信号不失真，同时，当τ足够小时可滤除控制信号的高频部分，因为其高频部分会使悬架产生高频抖振。引入此低通滤波器取代具有不确定参数的系统模型，既保证系统的稳定性，又提高误差跟踪反推控制器的适用性。选取合适的τ，最终主动控制律设计为

(30)

3　仿真实验分析

在车辆主动悬架设计中，主要考虑的性能指标有：1)代表乘坐舒适性的车身加速度；2)影响车身姿态且与结构设计和布置有关的悬架动行程；3)代表轮胎在随机路面激励下的轮胎动位移。为分析误差跟踪反推控制对悬架性能的影响，下面主要针对上述指标进行仿真实验，并与被动悬架作比较。图5为悬架控制系统的Simulink仿真模型。悬架参数如表1所示，设计参数如表2所示。控制仿真模型的激励采用C级路面，车速取20 m/s.

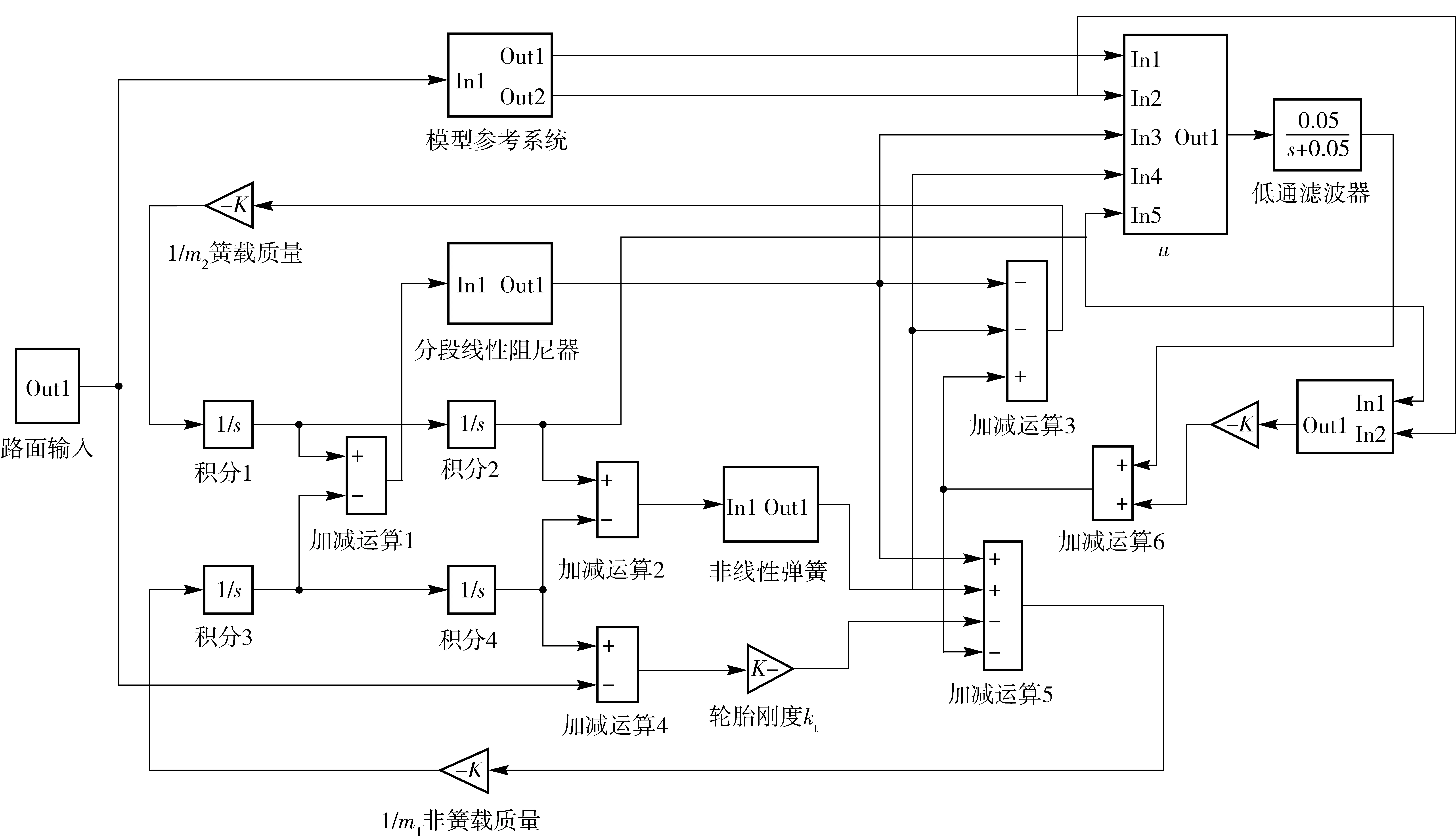
图5　悬架系统反推控制仿真模型Fig.5　Backstepping controller model of suspension system

3.1误差跟踪仿真分析

图6为车身位移误差ed追踪和车身速度误差ev追踪的仿真曲线。

从图6可以看出，跟踪误差ed和ev始终保持在一个很小的范围内，说明误差跟踪反推控制主动悬架系统能有效地跟踪模型参考系统。

3.2时域仿真分析

图7～图9是被动悬架和误差跟踪反推控制主动悬架的各性能参数时域仿真对比曲线，表3是时域仿真分析的统计结果。

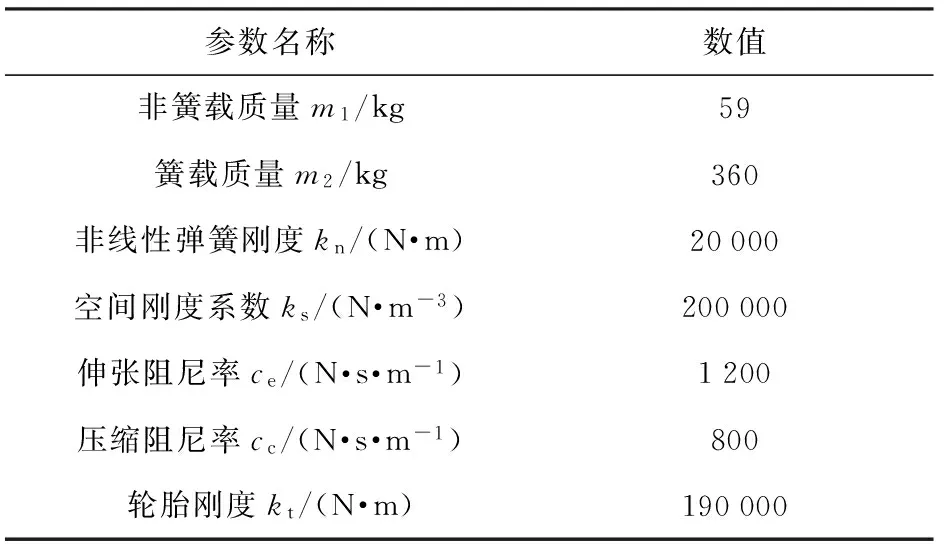
表1　2自由度主动悬架参数

表2　设计参数

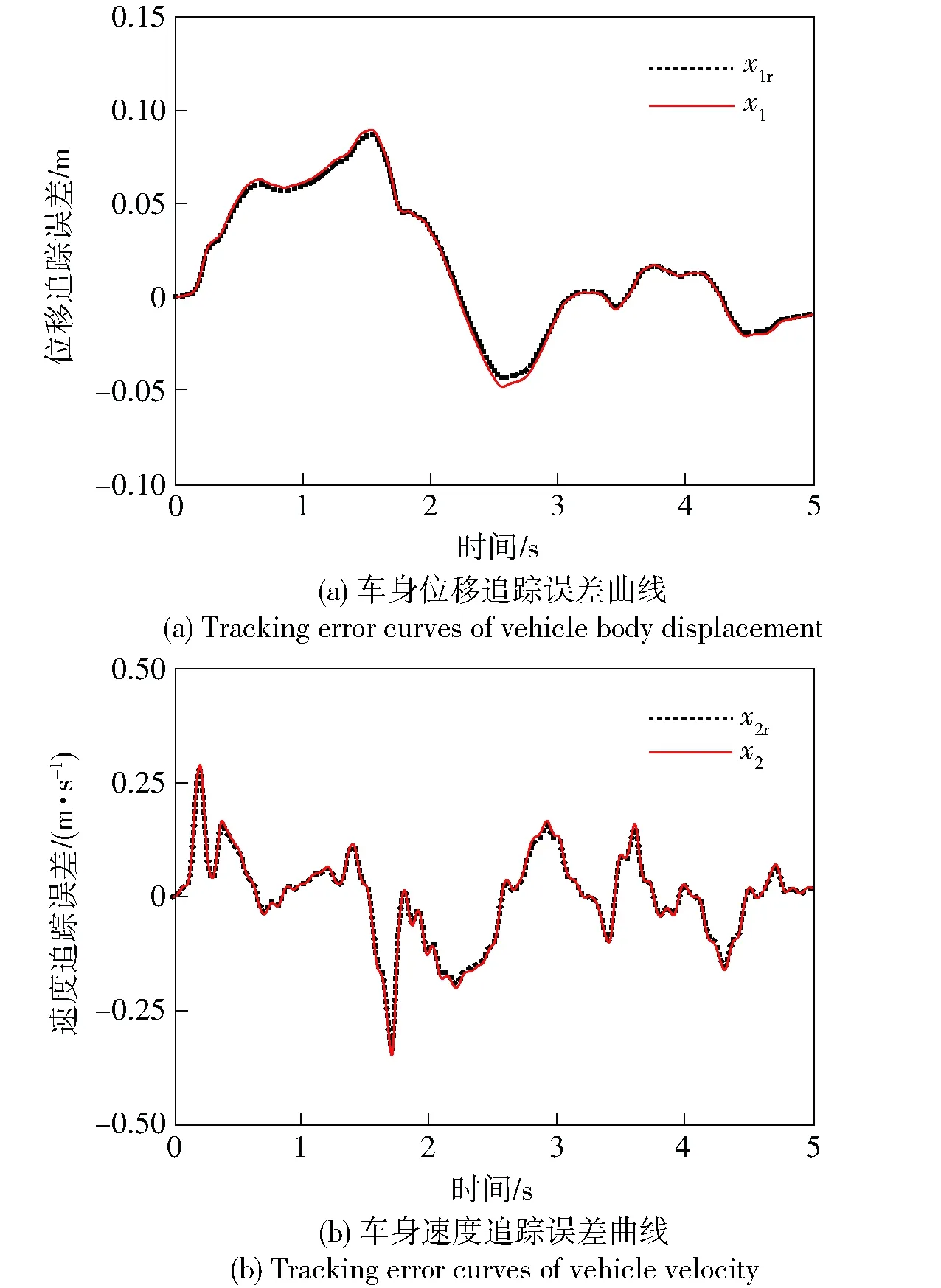
图6　车身位移与速度误差跟踪曲线Fig.6　　　　Tracking curves of vehicle body displacement and velocity

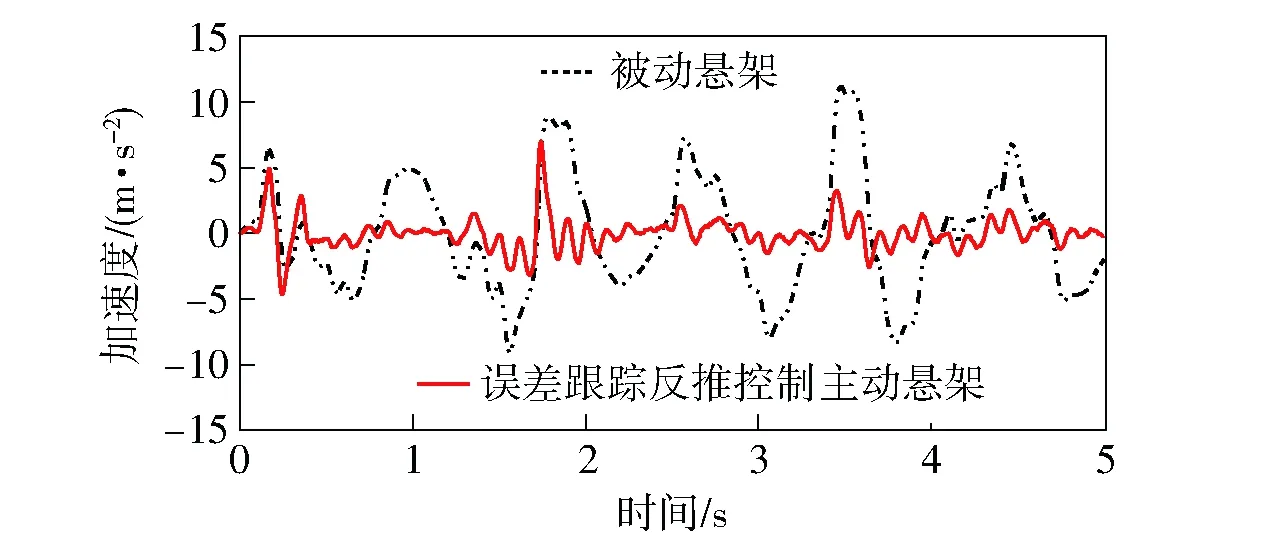
图7　车身加速度对比曲线Fig.7　Comparison of vehicle body accelerations

图8　悬架动行程对比曲线Fig.8　Comparison of suspension dynamic deflections

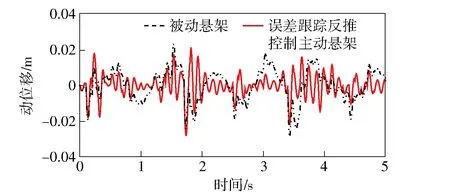
图9　轮胎动位移对比曲线Fig.9　Comparison of tire dynamic displacements

从图7～图9可以看出，相较于被动悬架，误差跟踪反推控制主动悬架的性能有明显改善，由表3可以得到主动悬架的车身垂向加速度、悬架动行程和轮胎动位移的均方根值相较被动悬架分别下降73.56%、27.22%和24.18%，这不但减小悬架动行程和轮胎动位移，避免悬架动行程超出限定范围而撞击限位块导致悬架击穿现象的发生，同时也提高了车辆操纵稳定性。

3.3频域仿真分析

车身、悬架和车轮的频率响应特性影响着整车的平顺性，为了进一步分析误差跟踪反推控制器对主动悬架性能的改善，对悬架各项性能指标进行了频域仿真分析，仿真分析结果如图10所示。

人体内脏和脊椎系统最敏感的振动频率范围为4.0～12.5 Hz，引起车身共振的频率范围为1.0～1.5 Hz. 从图10中可知，在最容易引起人体内脏和脊椎系统以及车身共振的低频区，误差跟踪反推控制主动悬架的车身加速度性能指标明显优于被动悬架，表明在低频区误差跟踪反推控制器可以有效抑制车身与人体内脏和脊椎系统共振。轮胎动位移在低频区也得到了一定改善，提高了车辆操稳性，但是在高频区有一定恶化。

表3　时域分析统计结果

注：1)表中车身加速度、悬架动行程和轮胎动位移的变化情况各有两栏数据，左栏表示两种主动悬架相对被动悬架控制变化的百分比，右栏则表示误差跟踪反推控制主动悬架相对模型参考系统控制变化的百分比；2)变化情况栏中“+”表示恶化，“-”表示改善。

图10　频域分析仿真结果Fig.10　Frequency domain analysis results

图11　变车速、路面仿真结果Fig.11　　　　Analysis results with various speed and various road inputs

3.4不同车速、路面下悬架性能仿真分析

为了分析误差跟踪反推控制器对车速、路面不确定性的控制效果，分别取20 m/s、25 m/s、30 m/s、35 m/s车速对理想、A级、B级、C级、D级5种路面模型输入进行仿真，并计算了车身加速度、悬架动行程和轮胎动位移的均方根值，其控制效果如图11所示。

从图11可以看出，在车速确定的情况下，随着路面等级降低，车身加速度和悬架动行程均方根值呈增加趋势；相较于被动悬架，误差跟踪反推控制主动悬架始终保持着较低的车身加速度值和悬架动行程，且波动平稳，说明施加控制后的悬架对于车速和路面的不确定性表现出较好的自适应性和鲁棒性。

4　结论

1)本文针对1/4车辆主动悬架动力学模型，引入非线性弹簧模型和分段线性阻尼器模型，与传统悬架模型相比，在一定程度上消除了简化误差，使计算和仿真结果更加接近实际情况。

2)针对如何协调控制车身垂直加速度与悬架动行程之间的矛盾，通过反推控制理论，设计一个理想模型参考系统，并通过模型参考方法，设计了一种误差跟踪反推控制器，简化了模型参考系统，在实际工程中较容易实现，并滤除了汽车主动悬架系统中的不确定性参数，避免了有害的高频信号，增强了系统稳定性。

3)仿真实验表明，误差跟踪反推控制器能够有效抑制车身垂直加速度、悬架动行程，不但解决了车身垂直加速度与悬架动行程之间冲突的问题，而且在路面状况和车速发生改变时仍保持良好的控制效果。

4)轮胎动位移控制效果并不十分明显，如何通过反推控制进一步解决车辆操纵稳定性与舒适性之间的矛盾，是本文下一步研究的重点。

References)

[1]Sakthivel R, Arunkumar A, Mathiyalagan K, et al. Robust reliable control for uncertain vehicle suspension systems with input delays[J]. Journal of Dynamic Systems, Measurement, and Control, 2015, 137(4):1-13.

[2]Guo L X, Zhang L P. RobustH∞control of active vehicle suspension under non-stationary running[J]. Journal of Sound and Vibration, 2012, 331(26):5824-5837.

[3]龙垚坤, 文桂林, 陈哲吾. 汽车主动悬架鲁棒保性能控制仿真研究[J]. 汽车工程, 2014, 36(2): 216-221.

LONG Yao-kun, WEN Gui-lin, CHEN Zhe-wu. A simulation study on robust guaranteed cost control for vehicle active suspension[J]. Automotive Engineering, 2014, 36(2):216-221.(in Chinese)

[4]杨柳青, 陈无畏, 高振刚, 等. 基于电磁阀减振器的1/4车辆半主动悬架非线性控制[J]. 农业机械学报, 2014, 45(4):1-7,36.

YANG Liu-qing, CHEN Wu-wei, GAO Zhen-gang, et al. Nonlinear control of quarter vehicle model with semi-active suspension based on solenoid valve damper[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(4):1-7, 36.(in Chinese)

[5]付振, 楼少敏, 许沧粟. 基于参考模型的半主动悬架滑模控制[J]. 汽车工程, 2009, 31(6): 552-556.

FU Zhen, LOU Shao-min, XU Cang-su. Sliding mode control of semi-active suspension based on reference model[J]. Automotive Engineering, 2009, 31(6):552-556. (in Chinese)

[6]Lian R J. Enhanced adaptive self-organizing fuzzy sliding-mode controller for active suspension systems[J]. IEEE Transactions on Industrial Electronics, 2013, 60(3):958-968.

[7]马吴宁, 徐诚, 郭亚军. 火箭炮位置跟踪双自由度反推控制方法[J]. 兵工学报, 2013, 34(4): 484-489.

MA Wu-ning, XU Cheng, GUO Ya-jun. Method of double degrees of freedom backstepping control for position tracking of rocket launcher[J]. Acta Armamentarii, 2013, 34(4):484-489.(in Chinese)

[8]高剑, 赵宁宁, 徐德民, 等. 水下航行器轴向运动的自适应积分反演跟踪控制[J]. 兵工学报, 2008, 29(3):374-378.

GAO Jian, ZHAO Ning-ning, XU De-min, et al. Adaptive integral backstepping surge motion tracking control for an underwater vehicle[J]. Acta Armamentarii, 2008, 29(3):374-378.(in Chinese)

[9]Fialho I, Balas G J. Road adaptive active suspension design using linear parameter varying gain-scheduling[J]. IEEE Transactions on Control Systems Technology, 2002, 10(1):43-54.

[10]管成, 朱善安. 车辆主动悬架路面自适应控制系统[J]. 农业机械学报, 2005, 36(7): 20-24.

GUAN Cheng, ZHU Shan-an. Study on road self-adaptive control of vehicle active suspension[J]. Transactions of the Chinese Society for Agricultural Machinery, 2005, 36(7):20-24.(in Chinese)

[11]Sun W C, Gao H J, Kaynak O. Adaptive backstepping control for active suspension systems with hard constraints[J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(3):1072-1079.

[12]Sun W C, Pan H H, Zhang Y F, et al. Multi-objective control for uncertain nonlinear active suspension systems[J]. Mechatronics, 2014, 24(4):318-327.

[13]Wai R J, Yao J X, Lee J D. Backstepping fuzzy neural network control design for hybrid maglev transportation system[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(2):302-317.

[14]张鹏, 李颖晖, 肖蕾. 基于递归神经网络的伺服系统自适应反步控制[J]. 系统仿真学报, 2008, 20(6):1475-1478.

ZHANG Peng, LI Ying-hui, XIAO Lei. Adaptive backstepping control for servo system based on recurrent neural network[J]. Journal of System Simulation, 2008, 20(6):1475-1478.(in Chinese)

[15]董文瀚, 孙秀霞, 林岩. 一种Backstepping模型参考鲁棒飞行控制律的设计[J]. 系统工程与电子技术, 2010, 32(7):1485-1488.

DONG Wen-han, SUN Xiu-xia, LIN Yan. Backstepping model reference robust controller design for flight control[J]. Systems Engineering and Electronics, 2010, 32(7):1485-1488.(in Chinese)

[16]Yagiz N, Hacioglu Y. Backstepping control of a vehicle with active suspensions[J]. Control Engineering Practice, 2008, 16(12):1457-1467.

[17]Lin J S, Kanellakopoulos I. Nonlinear design of active suspensions[J]. IEEE Transactions on Control Systems Magazine, 1997, 17(3):45-59.

Backstepping Controller Design for Nonlinear Active Vehicle Suspension Based on Model Reference Control

PANG Hui, CHEN Jia-nan, LIANG Jun, CHEN Ying

(School of Mechanical and Precision Instrument Engineering, Xi’an University of Technology, Xi’an 710048，Shaanxi, China)

The parameter uncertainties of vehicle suspension system are studied, and a novel backstepping controller design method based on model reference control (MRC) is proposed for nonlinear active vehicle suspension A nonlinear dynamics model of the suspension system is established, and high-pass and low-pass filters are introduced. The pass bandwidths of the high-pass and low-pass filters are changed according to suspension dynamic deflection. An ideal MRC system is designed. On this basis, both the tracking errors of vehicle body displacement and vertical velocity are constructed for the controlled suspension system and MRC system, and a backstepping controller of tracking error is proposed based on backstepping technique and Lyapunov stability theory. The effectiveness and tracking accuracy of the proposed approach are verified through numerical simulation.

ordnance science and technology; nonlinear active suspension; backstepping control; tracking error; model reference control

2016-02-15

国家自然科学基金项目(51305342)；陕西省自然科学基金项目(2014JQ7240)；陕西省教育厅科研计划项目(2013JK1027)；西安理工大学科研基金项目(2015cx004)

庞辉(1980—)，副教授， 博士。 E-mail:huipang@163.com

U463.33+1

A

1000-1093(2016)10-1761-09

10.3969/j.issn.1000-1093.2016.10.001