岩石动力学计算中的网格效应及机理研究

王海兵， 张海波， 田宙， 欧卓成， 周刚

(1.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081; 2.西北核技术研究所, 陕西 西安 710024)



岩石动力学计算中的网格效应及机理研究

王海兵1,2， 张海波2， 田宙2， 欧卓成1， 周刚2

(1.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081; 2.西北核技术研究所, 陕西 西安 710024)

岩石动力学计算中，网格尺寸对数值计算结果的可靠性有重要影响。采用数值实验的方法，对岩石爆炸应力波传播数值计算中的网格尺寸效应及其敏感性机理进行了研究。研究结果表明：合适的网格尺寸要根据载荷特征和波传播介质的属性来决定；当一个载荷波长内的网格数达到16个以上时，计算得到的各物理量的波形和峰值基本趋于稳定；计算还给出了各物理量与网格密度的关系；随着爆心距的增加，物理量对网格尺寸的敏感性降低，其机理是载荷中的高频成分逐渐衰减、载荷的波长变大，模型所需的网格尺寸变大；时间步长系数对计算结果的影响也非常明显，当时间步长系数取0.05时，位移稳态值趋于收敛值。

兵器科学与技术； 数值计算； 网格尺寸； 时间步长； 敏感性机理

0　引言

岩石中的爆炸动力学问题广泛应用于国家经济建设、国防军事以及科研领域等方面。岩石中的爆炸动力学过程非常复杂，通常很难进行精确地解析求解，数值计算是常用的有效手段。该方面的计算主要涉及三方面的物理过程：一是炸药的起爆及爆炸产物与冲击波在爆室内的传播；二是爆炸产物及冲击波与围岩的相互作用；三是围岩的动态响应。与这三方面物理过程相对应的三类计算问题为：爆炸载荷的求解问题、爆炸载荷与围岩的能量耦合问题以及应力波在围岩中的传播问题。计算这些问题常用的数值方法是有限差分方法和有限元方法。与有限差分相比，有限元方法具有灵活的网格划分、边界条件和边界形状的处理等优点，现在已成为爆炸动力学中的重要数值方法。通常来讲，数值计算的精度依赖于描述材料行为所采用的数学模型，如本构关系和状态方程等。由于目前描述爆炸作用下材料响应的数学模型还不完善，且都是近似的，因此数值分析的精度一般不高于近似方程的精度[1]。如果不考虑数学模型的近似程度，单从数值计算的角度讲，一种算法的稳定性与精度决定于[2]：1)积分格式与其所用的参数；2)时间步长；3)计算模型所划分的网格尺寸。

由于爆炸波持续时间非常短并且能量在不同的网格之间传输，数值模拟结果对有限单元的尺寸非常敏感，数值结果的精度强烈地依赖于所使用的网格尺寸。通常需要开展网格尺寸收敛性测试以获得合适的网格尺寸。爆炸冲击波数值模拟中网格尺寸效应研究的核心问题就在于如何针对具体的爆炸问题确定合适的网格尺寸，以在确保数值模拟精度的同时尽可能地减少网格数量和提高计算效率。然而，由于各类介质的物理属性差异，使得针对某一种介质开展网格尺寸效应分析确定的网格尺寸在介质改变时，其适用性具有较大的局限性。采用同一网格尺寸模拟不同介质中的冲击波传播问题时，计算精度可能存在较大区别。因此，合适的网格尺寸不仅与所模拟的爆炸情况相关，还与爆炸冲击波的传播介质相关[3]。当爆炸载荷作用在爆室壁围岩时，就涉及流体与固体(简称流固)耦合问题，研究表明，流固耦合算法的选取及关键耦合参数的设置以及爆炸流体和围岩固体网格尺寸的相对大小，对计算结果都有很大的影响。限于篇幅限制，本文关于网格尺寸对流固耦合效果的影响暂不展开讨论，主要研究爆炸冲击波在空气中及岩石内传播的网格尺寸效应。

1　网格尺寸对爆炸场载荷计算的影响

爆炸载荷的确定依赖于爆炸场的求解，也直接影响着外围结构响应的计算和安全性评估的可靠性，因此准确的爆炸载荷计算非常重要。一般情况下，爆室或容器内的爆炸属于近区爆炸，在爆炸近区，爆轰产物的密度远高于空气密度，产物对爆炸载荷有着显著的影响。对此，国内外学者已开展了诸多研究，研究结果表明，在爆炸近区网格尺寸对计算结果的精度影响非常敏感。胡八一等[4]指出，要想模拟出来的反射冲击波压力峰值及波形与实测波形一致，最为关键的一点是爆室内或容器内部网格尺寸至少应小于或等于1 mm. Chapman[5]在用类似的商业软件计算冲击波超压时也发现当网格由10 mm细化到1 mm时，超压峰值提高了24.6%. 文献[6-7]的计算结果显示，采用LS-DYNA等商业软件计算得到的计算结果小于经验公式值，受软件和计算机硬件容量的限制，只能提供定性的计算结果，很难提供准确的定量计算。雷鸣等[8]采用Autodyn研究了网格大小对空中化爆自由场参数计算结果的影响，结果表明网格大小对质量守恒没有影响，对能量守恒有一定的影响，爆炸产物界面第一次扩张是在大约0.9 m/kg1/3爆心距位置附近，在比例距离1 m/kg1/3内每个单元取0.5 mm，在更远的区域每个单元5 mm计算得到的值与标准实验值较符合较好。姚成宝等[9]利用LS-DYNA计算空中爆炸时发现，网格尺寸在0.1～5 mm时计算结果差别不大，在网格尺寸小于1 mm时计算结果趋于收敛，当网格的密度尺寸小于5 mm/kg1/3时，计算结果基本趋于收敛，此时得到的结果基本满足精度要求。王海兵等[10]采用二维方法研究了容器内的爆炸载荷，结果指出：在比距离小于1.0 m/kg1/3时，2 mm的网格尺寸计算结果趋于收敛；在比距离大于1.0 m/kg1/3、网格尺寸取5 mm时，计算得到的峰值超压基本满足精度。Shi等[11]详细比较了网格尺寸对空中爆炸自由场诸参量的影响，图1～图3给出了其主要结果。图1给出了不同网格尺寸在比距离R为1 m/kg1/3处的正超压时程曲线比较，从图中可看出，随着网格尺寸的增加，压力p的上升率减缓、波形变得平缓、波幅拉宽，峰值降低；但波前到达时间和正压作用时间与网格尺寸无关。图2为峰值超压与网格尺寸和比距离的关系，从图中看出，当比距离小于0.8 m/kg1/3时，即使5 mm的网格尺寸也不能准确计算峰压；而当比距离超过2 m/kg1/3时，100 mm的网格尺寸也能准确地计算峰压。图3给出了正压冲量I与网格尺寸和比距离的关系，从图中看出，正压冲量与网格尺寸基本无关，100 mm的网格尺寸已能达到计算收敛。总结以上学者的研究结果，可以得到以下结论：当爆炸近区的网格尺寸取毫米量级时，可使计算获得的所有力学参量符合实测；随着网格尺寸的增加，压力的上升率减缓、波形变得平缓、波幅拉宽，峰值降低；超压峰值对网格的敏感性很高，随着比距离的增加，超压峰值对网格的敏感降低；超压峰值和压力上升率是网格密度的正相关量，而波前到达时间、正压作用时间、正压冲量等是网格尺寸的无关量。

图1　　　　不同网格尺寸在比距离1 m/kg1/3处的正超压时程曲线比较[11]Fig.1　　　　Comparison of pressure-time histories obtained with different mesh sizes at scaled distance of 1 m/kg1/3[11]

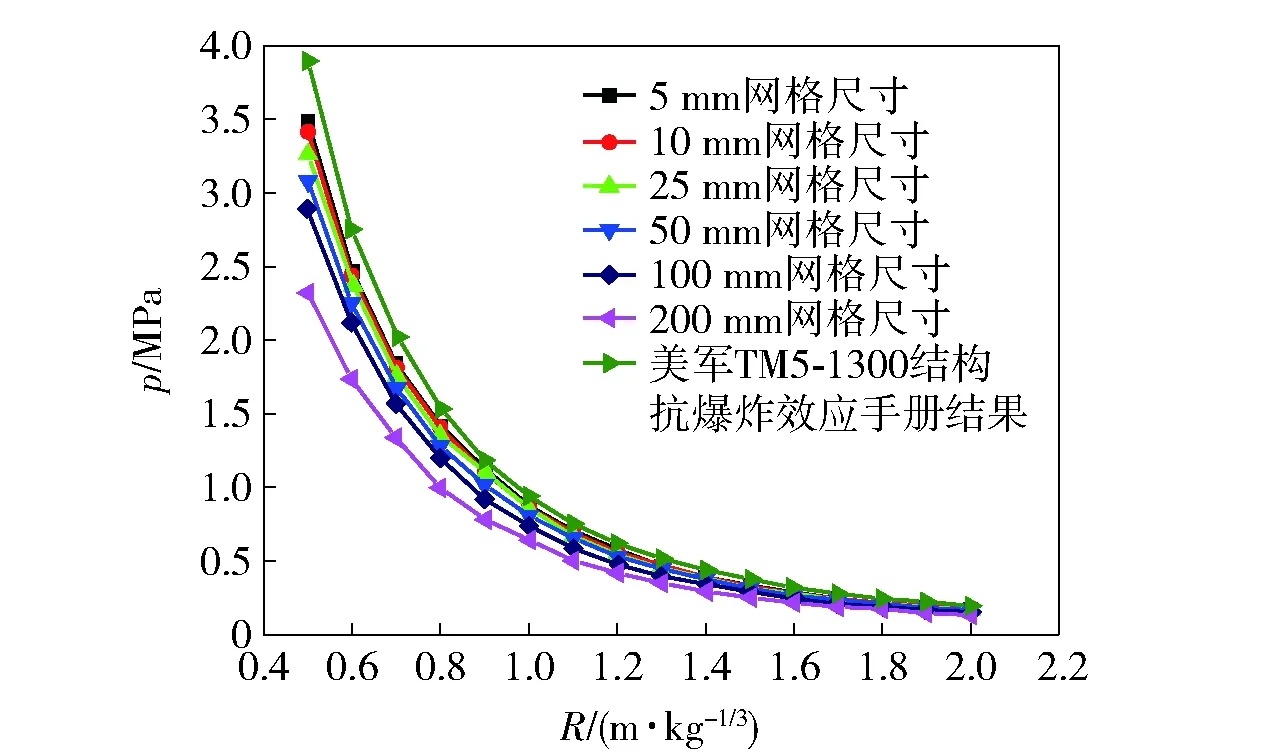
图2　峰压与网格尺寸和比距离的关系[11]Fig.2　　　　Variation of the positive incident peak pressure with mesh size and scaled distance[11]

图3　正压冲量与网格尺寸和比距离的关系[11]Fig.3　　　　Variation of normalized positive incident impulse with mesh size and scaled distance[11]

在实际应用中，要使计算达到工程使用价值，计算模型的尺度至少要达到1～10 m的范围，在如此大的范围内，若将所有的力学参量都计算准确，需要将单元尺寸细化到毫米量级。对于三维计算，即使采取1/8对称模型，网格数量也将达到109～1012个量级左右。这样的计算规模即使采用目前最为先进的巨型工作站进行计算，也绝非易事。但通常关注的效应是爆炸作用下的结构响应，而决定结构响应的参量是正压冲量。前文的网格收敛性计算说明，正压冲量是网格尺寸的不敏感量，100 mm的网格尺寸已经能基本满足计算精度要求。所以，当计算规模较大时，虽然由于网格尺寸限制，不能对超压峰值进行准确计算，但仍然能够准确计算正压冲量，进而能够获得准确的爆炸效应。文献[11]还提出一种网格尺寸效应的数值修正方法，其原理是利用网格尺寸的不敏感量来修正网格尺寸敏感量，从而提高大网格尺寸情况下有限元模拟结果的精度。具体方法是通过冲量等效的原理来修正超压峰值，修正后，即使采用200 mm的网格尺寸也能得到较为精确的超压峰值。

2　网格尺寸对岩石中应力波传播计算的影响

关于网格尺寸对岩石动力学计算的影响，已有学者开展了相关的研究。梁正召等[12]讨论了非均匀性岩石中网格尺寸对裂纹扩展即岩石破裂的影响，研究认为，随着网格尺寸的减小，岩石强度逐渐降低，并趋于稳定；在均质岩石中，网格尺寸主要和结构特征相关；在非均质岩石中，网格尺寸还与材料的非均匀性和细观特征尺度密切相关，引入单元统计性的非均匀性后，单元尺寸必须接近细观特征尺度才能保证计算结果的稳定性和可靠性。崔焕平等[13]提出了把极限拉应变作为网格尺寸的函数，以保证混凝土开裂单位面积吸收的能量唯一，从而有效地消除混凝土非线性有限元分析中的网格尺寸效应。门建兵等[14]研究了网格对混凝土侵彻数值模拟的影响，研究认为弹丸半径方向要划分3个网格，靶板在弹丸半径尺寸方向上划分6个网格得到的计算结果比较理想。Shayanfar等[15]讨论了网格尺寸对载荷- 位移、载荷- 应变、裂纹模式和最终载荷的影响，并开发了一个简单的程序来计算混凝土的最终拉伸应变，以此来消除计算结果对网格尺寸的依赖，并将其嵌入到非线性有限元程序中。以上的研究大多都是通过网格的收敛性测试来获得合适的网格尺寸，然而对于大规模计算来讲，很难对模型进行整体的网格收敛性测试；另外，这些研究并未考虑载荷的特征，而爆炸冲击型载荷包含大量的高频分量，其输入荷载的波形与模型网格划分密切相关，如果不同时考虑荷载的频谱特性，在确定时间步长和网格划分时往往带有较大的盲目性，得到的结果也不具备一般通用性。因此，本文以输入载荷的特性为出发点，来研究网格尺寸对岩石中应力波传播计算的影响。

2.1典型的爆炸载荷特征

以1 t TNT爆炸为例，读取爆心距3.06 m位置处的压力波形如图4所示。从图4中的载荷等效曲线确定外载荷的周期约为300 μs.

图4　1 t TNT爆炸在3.06 m位置处的压力波形Fig.4　　　　Pressure waveform at 3.06 m from the distance of 1 t TNT explosive source

2.2岩石中的波速及波长

弹性波传播的速度不仅仅取决于波的类型，而且还与介质周围的条件有关。弹性纵波在单轴应变(相当于无限介质)条件下传播的速度为

(1)

式中：ρ、Λ和μ分别是介质的密度、拉梅常数和剪切模量；cim是弹性波在无限介质中的传播速度。

对于一维杆的波传播问题，根据波动方程，有

(2)

式中：E是弹性模量；codb是弹性波在一维杆中的传播速度。“无限介质”和“杆”等模型都是一些极限情况的近似，所谓“无限介质”是指在物理上介质的尺度远远大于所传播波的波长，“杆”是指介质的横向尺度远远小于波的波长。通常研究的介质其尺度各不相同，研究的波长也从地震波的几百千米至实验室内超声波波长的几个毫米乃至几微米不等。因此，在讨论波速及波传播问题时，需要研究介质的尺度与波长λ大小的相互关系。取花岗岩参数：密度为2.62 g/cm3，泊松比υ为0.24，弹性模量为58.7 GPa. 再根据弹性力学关系式：

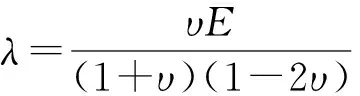
(3)

(4)

得到弹性纵波在花岗岩无限介质中的传播速度cim=5 138 m/s，在花岗岩中一维杆的波速codb=4 733 m/s.

因此，2.1节中的爆炸载荷在花岗岩无限介质中传播的波长为

λim=cimT=1.541 4 m，

(5)

式中：T为载荷加载周期。

在花岗岩介质一维杆中传播时的波长为

λodb=codbT=1.419 9 m.

(6)

由此看到，应力波的波长由外载荷和传播介质的属性共同决定。

2.3岩石中波传播计算所需的网格尺寸

下面研究当网格尺寸取多少时，岩石中的波传播计算结果趋于稳定。

建立一维杆模型，计算杆中的弹性波传播问题。在杆的端部施加半周期正弦载荷F=Asinωt，其中，A为振幅，ω为角频率，频率f=1/T=ω/2π. 取T=300 μs，A=10 MPa，低于岩石强度，弹性加载。输入的加载波形如图5所示。

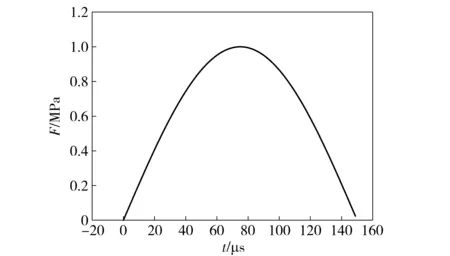
图5　输入的压力加载波形Fig.5　Loading waveform of input pressure

区别于大多数文献中通过逐渐减小网格尺寸加密网格数来获得网格收敛性结果的方法，本文将网格尺寸和载荷波长相关联，研究一个波长长度内不同网格数对计算各物理量的影响。取网格尺寸Δl=λ/n，其中n为网格密度数，表示一个波长长度内的网格数，λ取花岗岩一维杆中的波长1.419 9 m.n分别取2、4、8、16、20、40和60.

2.3.1网格尺寸对压力波形的影响

图6给出了一个波长范围内取不同网格数计算得到的压力波形比较。从图6中可以看出：压力的波形和峰值对网格密度非常敏感，当一个波长内的网格达到16个时，压力波形和峰值基本趋于稳定；随着网格密度的增大，压力波形的首峰上升率增大、振荡次数减少、振荡频率减小；压力波形以最终稳态值为中心进行振荡，不同网格密度计算得到的最终压力稳态值相同。

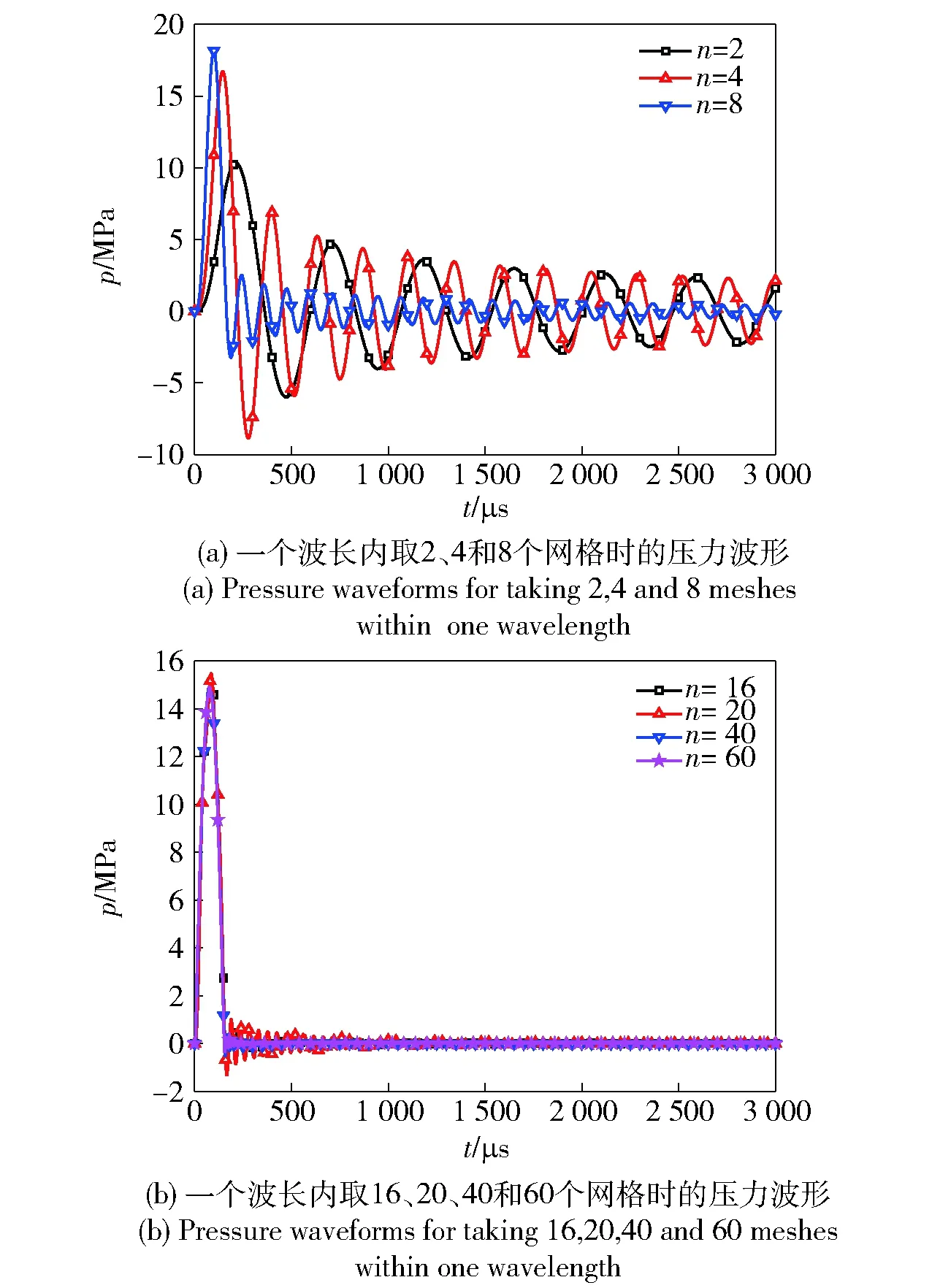
图6　　　　一个波长范围内取不同网格数计算得到的压力波形比较Fig.6　Comparison of pressure waveforms obtained from different grid number within a wavelength range

2.3.2网格尺寸对速度波形的影响

图7给出了一个波长范围内取不同网格数计算得到的速度v波形比较。从图7中可以看出：随着网格密度的增大，速度峰值逐渐增大，速度波形的首峰上升率增大；当网格密度达到16时，速度峰值和波形基本趋于稳定值；随着网格密度的增大，速度波形的振荡(次数和周期)逐渐减少。

图7　一个波长范围不同网格数计算得到的速度波形比较Fig.7　Comparison of velocity waveforms obtained from different grid numbers within a wavelength range

2.3.3网格尺寸对位移波形的影响

图8给出了一个波长范围内取不同网格数时计算得到的位移D波形比较。从图8中可以看出：随着网格密度的增大，位移峰值逐渐减小、首峰上升率增大、位移波形的振荡周期逐渐减小、振荡次数逐渐减少；当每个波长内的网格数量达到16时，位移峰值和波形基本趋于稳定；比较不同网格密度的位移波形可以看到，虽然波形不同、振荡周期不同，但位移的稳态值基本相同(振荡波形取稳态值为波峰或波谷间的平均值)。由此可认为，位移的波形和峰值受网格尺寸影响明显，但位移稳态值与网格尺寸无关，稳态位移值是网格无关量。为证明该结论的正确性，下面进行进一步计算验证。

图8　　　　一个波长范围不同网格数计算得到的位移波形比较Fig.8　Comparison of displacement waveforms obtained from different grid numbers within a wavelength range

首先进一步减小网格密度(增大网格尺寸)，比较位移波形和稳态值。计算中增加杆长、增加计算时间，将网格密度进一步减小到一个波长一个网格和两个波长一个网格，比较不同网格密度计算得到的位移波形，如图9所示。图9中标出了不同网格密度计算得到的位移稳态值，从图中看到，不同网格密度计算得到的位移稳态值完全相同。

图9　一个波长范围内不同网格数计算得到的位移波形比较Fig.9　Comparison of displacement waveforms obtained from different grid numbers within a wavelength range

另外，为了验证加载波类型对结论的影响，将加载波由半周期正弦波改为单脉冲方波，对不同网格密度进行计算验证，计算得到了同样的结论：当一个波长内的网格数从1个增加到32个时，计算得到的稳态位移值完全相同；但网格密度不同，计算到达稳态位移所需的时间不同，网格密度越大，计算达到稳态位移的时间越短。该验证说明，获得的上述结论和加载波的类型无关。

从能量的角度可以解释稳态位移计算结果的网格无关性。对各种不同的网格密度模型输入的外力载荷相同，因此对模型做的总功相同。而功等于力与位移的乘积，如果计算中能量守恒，输入的外载荷又相同，那么得到的稳态位移值一定相等。

2.3.4岩石中爆炸波传播计算所需的网格尺寸

根据2.3.3节得到的结论，当一个波长内的网格数达到16个时，计算波形基本趋于稳定，计算结果基本收敛，可以推算花岗岩无限介质中爆炸波传播计算所需的网格尺寸为

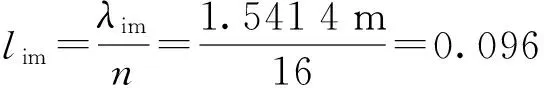
(7)

花岗岩介质中一维杆波传播计算所需的网格尺寸为

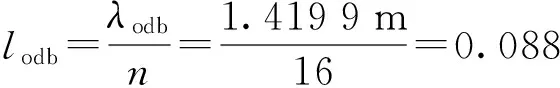
(8)

根据计算得到的网格尺寸，测试围岩自由场计算精度，结果如图10所示，图中，vmax为速度峰值，d为爆心距。从图10中看到，10 cm的网格尺寸，基本能满足计算精度要求。

图10　　　　1 t TNT填实爆炸时的不同网格尺寸自由场速度峰值比较Fig.10　　　　Comparison of free field peak velocities with different mesh size of 1 t TNT tamped explosion

3　网格尺寸敏感性机理分析

从2.3.3节和2.3.4节的分析看到，对于网格敏感量(以压力p为例)，爆心距越小计算所需的网格尺寸越小，说明在不同的爆心距，物理量对网格的依赖程度不一样。文献[16]在研究空气和水下爆炸时指出，采用同一网格尺寸，在炸药量较大的情况下可以获得较为精确的数值结果，而炸药量较小时与经验公式计算值偏离较大，即炸药当量均对数值计算的精度有较大影响——炸药当量越大，可使用的网格尺寸越大。由此产生疑问：当量对计算网格产生影响的原因是什么？进而还产生疑问，为什么计算相同的物理量在不同爆心距对网格的尺寸要求不同？为此进行了网格尺寸的敏感性机理分析。

首先分析不同炸药当量产生的差别。从爆炸缩比规律来讲，压力波的作用时间和当量的三分之一次方呈正比。所以爆炸当量越大，产生的爆炸载荷波长越长。而之前的研究结果表明，当一个波长内的网格数目大于等于16个时，基本能够准确模拟各种物理量。波长越长，相应的模拟所需的网格尺寸也就越大，因此，对于同一网格尺寸，爆炸当量越大，模拟的结果越精确。

为研究物理量在不同爆心距对网格尺寸的依赖程度不同，本文采用1 mm大小的网格尺寸计算得到TNT空中爆炸时不同比例爆心距R的速度波形(如图11所示)，并对其进行了频谱分析(如图12所示)。从图12看到，随着爆心距的增大，速度波形中的高频分量逐渐减小，而低频分量相对逐渐增多。通常来讲，爆炸载荷是由多种频率的波叠加而成，高频波波长短，模拟所需的网格尺寸较小，而高频波衰减较快，随着爆心距的增加，高频波成分逐渐减小，低频波相对成分逐渐增加，因此随着爆心距的增大，加载波的波长逐渐增加，模拟所需的网格尺寸逐渐增大，因此，随着爆心距的增大，物理量对网格尺寸的依赖性逐渐降低。

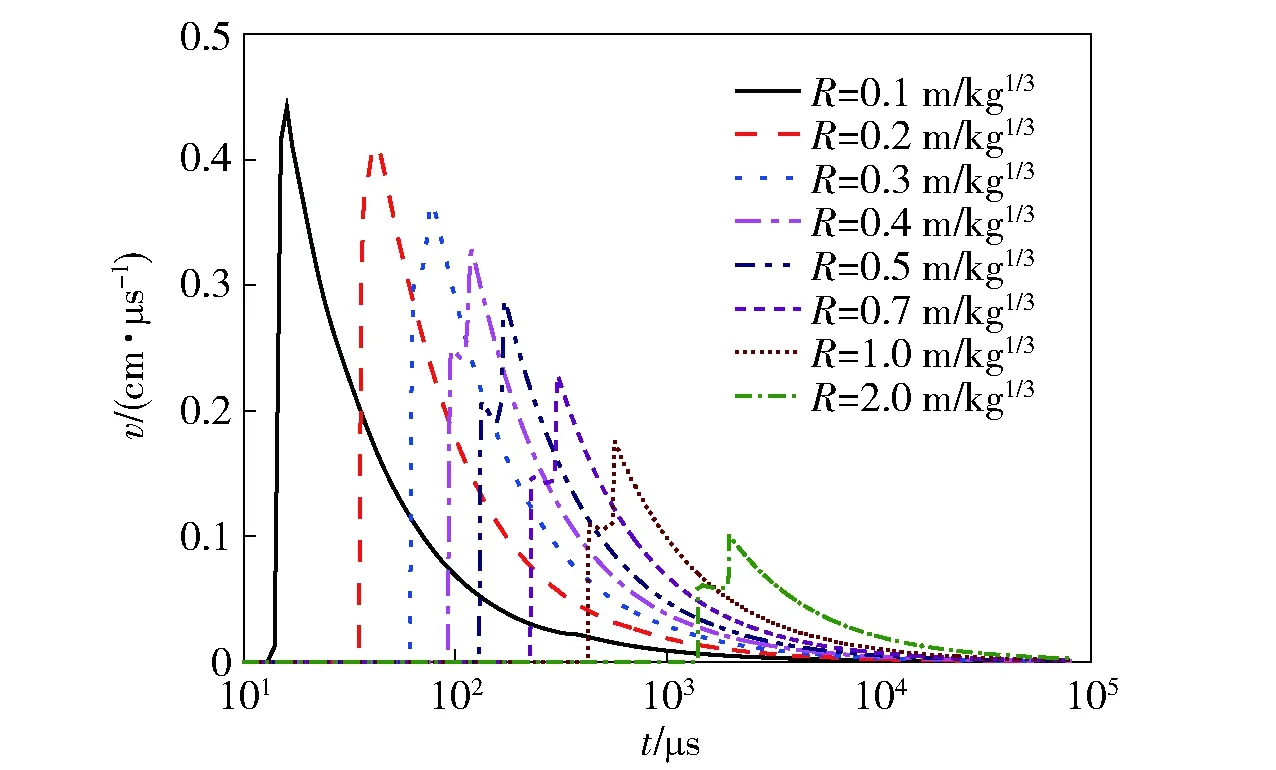
图11　TNT爆炸时不同比例爆心距的速度波形Fig.11　　　　Velocity waveforms at different scaled distances from explosive source during TNT explosion

图12　TNT爆炸时不同比例爆心距的速度波形频谱分析Fig.12　Spectral analysis of velocity waveforms at different scaled distances from explosive source during TNT explosion

图13为对某次化爆实验实测的不同爆心距位置的地震速度波形进行频谱分析得到的速度谱图像。从图中看到，随着爆心距的增加，振幅峰值前移，说明随着爆心距的增加高频分量耗散的较多，低频份额相对增加。由此导致整体的爆炸波载荷频率降低，波长增大，从而导致对计算网格尺寸的要求也越来越低，所以会出现随着爆心距的增加，计算网格尺寸的依赖性降低的现象。从理论上讲，根据不同爆心距位置冲击波的优势频率和波长确定合适的网格尺寸更接近问题的本质。然而冲击波的高频成分特别丰富，且高频分量衰减较快，如何确定不同爆心距处的优势波长尚存在一定困难。虽然目前可以通过网格渐变的划分方法来定性描述物理量随着爆心距的增大对网格的依赖性降低的现象，但如何准确地决定网格渐变率仍然有待深入研究。

图13　岩石中爆炸时不同爆心距的速度谱分析Fig.13　Spectral analysis of velocity waveforms at different scaled distances from explosive source during explosion in rock

4　时间步长系数对计算结果的影响

在动力学问题中，时间步长大致等于以声速通过单元最小特征长度所需的时间，计算中一般采用显式方法进行求解。在显式积分方法中，为保证算法的稳定性，积分步长是由最小单元的尺寸控制的。中心差分法是最常用的显式方法。中心差分法的临界时间步长取决于单元的特征长度。在小变形问题中，单元的特征长度不变，因此在整个求解过程中可以采用相同的时间积分步长。但在大变形问题中，单元的特征长度不断减小，因此中心差分法的临界时间步长也不断减小，需要采用变步长的中心差分法。LS-DYNA3D程序采用的就是变步长增量解法。对于三维实体单元，其极限时间步长采用如(9)式算法[17]：

(9)

式中：Q是体黏性系数C0和C1的函数，其表达式为

(10)

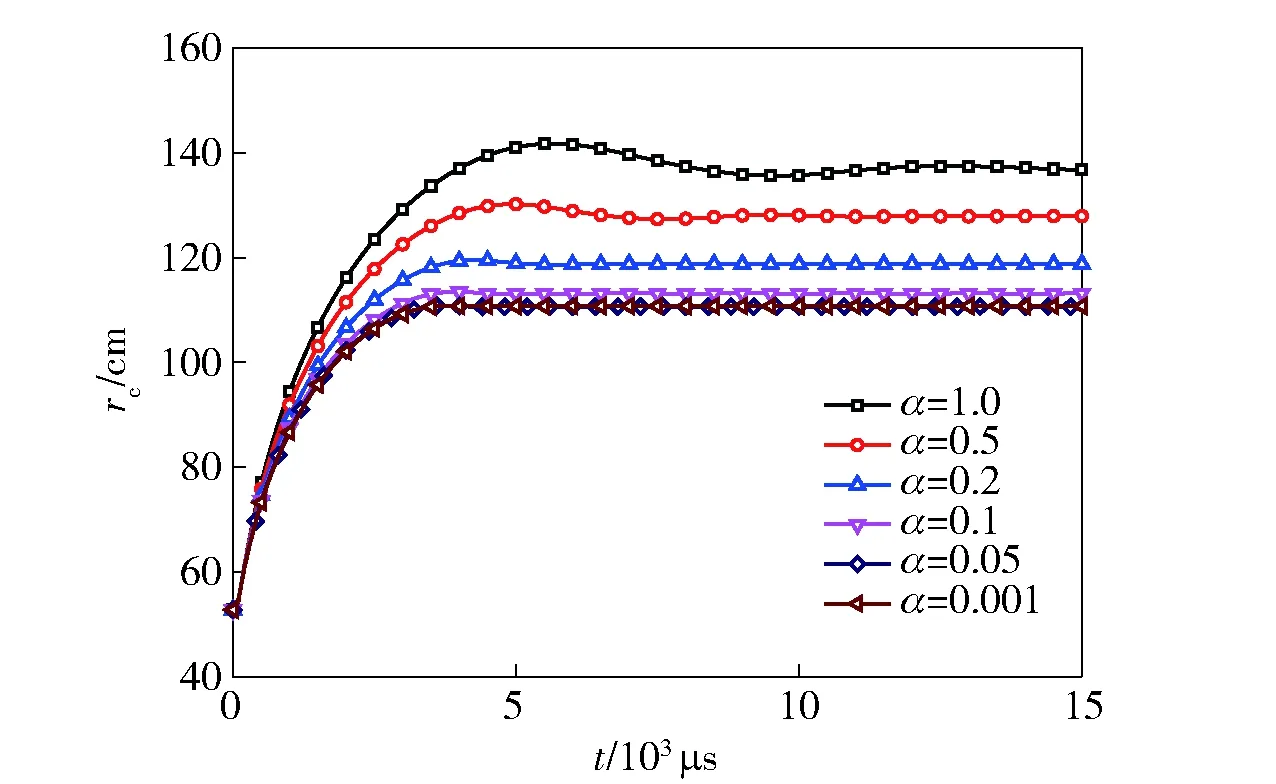
图14　不同时间步长系数计算得到的空腔半径比较Fig.14　　　　Comparison of calculated cavity radii with different time step coefficients

5　结论

本文通过对岩石中爆炸应力波传播数值计算中的网格尺寸效应及物理量对网格尺寸的敏感性机理的研究，得到了以下结论：

1) 合适的网格尺寸应根据载荷特征和波传播介质的属性来决定。

2) 网格大小对压力、速度和位移波形的影响较大；当一个波长内的网格个数达到16个以上时，计算得到的压力峰值、速度峰值和位移峰值等参量基本趋于稳定。

3) 压力峰值、压力上升率、速度峰值等参量是网格密度的正相关量；压力脉宽、波形的振荡次数、振荡频率、波形稳定时间和位移峰值等参量是网格密度的负相关量；而波前到达时间、正压作用时间、正压冲量、位移稳态值和爆室内的稳定压力等参量是网格无关量。

4) 随着爆心距的增加，物理量对网格尺寸的依赖性降低，其机理是随着爆心距的增加，载荷中的高频成分逐渐衰减、载荷的波长变大，模拟所需的网格尺寸变大。

5) 步长系数对计算结果的影响也非常明显，当时间步长系数取0.05时，位移稳态值趋于收敛值。

本文通过对网格尺寸这一关键计算因素对计算结果影响的研究，了解了哪些物理量是计算的确定量，哪些物理量是计算的不确定量；网格尺寸对各种物理量影响规律的获得，对计算模型的修正及对计算结果的可靠性把握起了很大的提升作用，使大规模的定量计算应用于实际工程问题成为可能。

References)

[1]张雄, 王天舒. 计算动力学[M]. 北京: 清华大学出版社, 2007.

ZHANG Xiong, WANG Tian-shu. Computational dynamics[M]. Beijing: Tsinghua University Press, 2007. (in Chinese)

[2]陆金甫, 关治. 偏微分方程数值解法[M]. 北京:清华大学出版社, 2004.LU Jin-fu, GUAN Zhi. Numerical solution of partial differential equation[M]. Beijing: Tsinghua University Press, 2004. (in Chinese)

[3]李顺波, 东兆星, 齐燕军, 等. 爆炸冲击波在不同介质中传播衰减规律的数值模拟[J]. 振动与冲击, 2009, 28(7):115-117.

LI Shun-bo, DONG Zhao-xing, QI Yan-jun, et al. Numerical simulation for spread decay of blasting shock wave in different media[J]. Journal of Vibration and Shock, 2009, 28(7):115-117.(in Chinese)

[4]胡八一, 柏劲松, 刘大敏, 等. 爆炸容器的工程设计方法及其应用[J]. 压力容器, 2000, 17(2):39-41.HU Ba-yi, BAI Jin-song, LIU Da-min, et al. The engineering design method of explosion-containment vessel and its application[J]. Pressure Vessel Technology, 2000, 17(2): 39-41. (in Chinese)

[5]Chapman T C. Blast wave simulation using AUTODYN 2D: a parametric study[J]. International Journal of Impact Engineering, 1995, 16(5): 777-787.

[6]胡八一, 李平, 张振宇, 等.爆炸塔内壁特征点的反射压力数值模拟[J]. 计算力学学报, 2009, 26(4): 573-578.

HU Ba-yi, LI Ping, ZHANG Zhen-yu, et al. Numerical simulation of characteristic points reflective pressure on the inner surface of the explosion chamber[J]. Chinese Journal of Computational Mechanics, 2009, 26(4):573-578.(in Chinese)

[7]杨鑫, 石少卿, 程鹏飞, 等. 爆炸冲击波在空气中传播规律的经验公式对比及数值模拟[J]. 四川建筑, 2007, 27(5): 71-73.

YANG Xin, SHI Shao-qing, CHENG Peng-fei, et al. Numerical simulation and comparison with empirical formula on the law of shock wave generated by TNT explosions in air[J]. Sichuan Architecture, 2007, 27(5): 71-73.(in Chinese)

[8]雷鸣, 田宙, 张海波, 等. 网格疏密对空中化爆自由场参数计算结果的影响[R]. 西安:西北核技术研究所, 2005.

LEI Ming, TIAN Zhou, ZHANG Hai-bo, et al. Study on the effects of mesh density to the results of freefield parameters about explosion in air[R]. Xi’an:Northwest Institute of Nuclear Technology, 2005.(in Chinese)

[9]姚成宝, 王宏亮, 张柏华, 等. TNT空中爆炸冲击波传播数值模拟及数值影响因素分析[J]. 现代应用物理, 2014, 5(1): 39-44.

YAO Cheng-bao, WANG Hong-liang, ZHANG Bai-hua, et al. Numerical simulation of shock wave generated by TNT explosions in infinite air[J]. Modern Applied Physics, 2014, 5(1): 39-44.(in Chinese)

[10]王海兵, 曹渊, 张海波, 等. 5kg TNT当量爆炸容器力学响应数值模拟及参数敏感性分析[C]∥第二届全国爆炸容器专题研讨会论文集. 西安:西北核技术研究所, 2013.

WANG Hai-bing, CAO Yuan, ZHANG Hai-bo, et al. Numerical simulation on dynamic response of 5kg TNT equivalent explosion container and parameters sensitivity analysis[C]∥Proceedings of the Second National Symposium on Explosive Containers. Xi’an: Northwest Institute of Nuclear Technology, 2013. (in Chinese)

[11]Shi Y C, Li Z X, Hao H. Mesh size effect in numerical simulation of blast wave propagation and interaction with structures[J]. Transactions of Tianjin University, 2008, 14(6): 396-402.

[12]梁正召, 王述红, 唐春安, 等. 非均匀性岩石破裂的网格效应[J]. 岩石力学与工程学报, 2005, 24(增刊1):5108-5112.

LIANG Zheng-zhao, WANG Shu-hong, TANG Chun-an, et al. Mesh effects on failure processes of heterogeneous rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(S1):5108-5112.(in Chinese)

[13]崔焕平, 崔燕平, 王宗敏. 混凝土非线性有限元分析中的网格尺寸效应[J]. 混凝土, 2007(6): 27-29.

CUI Huan-ping, CUI Yan-ping, WANG Zong-min. Mesh size effect in nonlinear finite element analysis of concrete[J]. Concrete, 2007(6): 27-29.(in Chinese)

[14]门建兵, 隋树元, 蒋建伟, 等. 网格对混凝土侵彻数值模拟的影响[J]. 北京理工大学学报, 2005, 25(8):659-662.

MEN Jian-bing, SUI Shu-yuan, JIANG Jian-wei, et al. Mesh dependency for numerical simulation of concrete penetration[J]. Transactions of Beijing Institute of Technology, 2005, 25(8):659-662.(in Chinese)

[15]Shayanfar M A, Kheyroddin A, Mirza M S. Element size effects in nonlinear analysis of reinforced concrete members[J]. Computers and Structures, 1997, 62(2): 339-352.

[16]张社荣, 李宏璧, 王高辉, 等. 空中和水下爆炸冲击波数值模拟的网格尺寸效应对比分析[J]. 水利学报, 2015, 46(3):298-306.

ZHANG She-rong, LI Hong-bi, WANG Gao-hui, et al. Comparative analysis of mesh size effects on numerical simulation of shock wave in air blast and underwater explosion[J]. Journal of Hydraulic Engineering, 2015, 46(3):298-306.(in Chinese)

[17]Hallquist J O. LS-DYNA theory manual[M]. Livermore, CA: Livermore Software Technology Corporation, 2006.

Mesh Size Effect and Its Mechanism Research in Numerical Calculation of Rock Dynamics

WANG Hai-bing1,2， ZHANG Hai-bo2， TIAN Zhou2， OU Zhuo-cheng1， ZHOU Gang2

(1.State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China; 2.Northwest Institute of Nuclear Technology, Xi’an 710024, Shaanxi, China)

In rock dynamics calculation, the mesh size has an important influence on the reliability of numerically calculated results. A numerical experimental method is used to research the mesh size effect and its sensitivity mechanism in the numerical simulation of propagation of explosion stress wave in rock. The research results show that a proper mesh size should be specified both by the load characteristics and the property of wave propagation medium. When the number of mesh is up to 16 within one load wavelength, the waveforms and peak values of all calculated physical quantities trend to be stable.The relationships between the values of physical quantities and the different mesh densities are also presented. With the increase in distance from explosive source, the sensitivity of physical quantities to mesh size decreases. This is because high-frequency components attenuate gradually, and the wavelength of load becomes longer with the increase in distance from explosive source. The time step coefficient also has a great influence on computational results. When the time step coefficient equals to 0.05, the stable value of displacement tends to converge.

ordnance science and technology; numerical calculation; mesh size; time step; sensitivity mechanism

2016-03-07

国家自然科学基金项目(91330205)

王海兵(1980—)，男， 博士研究生。E-mail: wanghaibing@nint.ac.cn；

欧卓成(1961—)，男，教授，博士生导师。E-mail: zcou@bit.edu.cn

O383+.1

A

1000-1093(2016)10-1828-09

10.3969/j.issn.1000-1093.2016.10.009