某大口径火炮弹带热力耦合挤进动力学数值模拟研究

李淼， 钱林方， 孙河洋

(1.南京理工大学 机械工程学院， 江苏 南京 210094; 2.军械工程学院 火炮工程系， 河北 石家庄 050003)



某大口径火炮弹带热力耦合挤进动力学数值模拟研究

李淼1， 钱林方1， 孙河洋2

(1.南京理工大学 机械工程学院， 江苏 南京 210094; 2.军械工程学院 火炮工程系， 河北 石家庄 050003)

为研究弹带挤进过程机理以及弹丸在挤进过程的运动规律，对大口径火炮挤进过程进行了仿真分析。考虑了火药气体在带锥度药室及坡膛内的分布，得到挤进时期的内弹道学方程，将该方程的解作为力边界条件，同时引入考虑温度的摩擦力模型来模拟身管与弹带间的摩擦，采用显式方法建立大口径火炮弹带挤进过程热力耦合仿真模型；分别对经典内弹道挤进过程和绝热挤进进行计算，验证了耦合计算的必要性；同时考虑不同弹炮间隙、卡膛速度以及初始摆角对挤进过程的影响，得到挤进过程中挤进阻力、弹丸速度、火药气体压力、弹丸摆角的变化规律。计算结果表明，弹炮间隙对挤进阻力和挤进速度有着重要的影响，而弹丸卡膛前摆角对弹丸挤进过程中的摆角有着重要的影响。

兵器科学与技术； 热力耦合； 挤进阻力； 弹丸姿态

0　引言

弹带挤进是在火药气体作用下弹带与身管内膛高速冲击，弹带瞬间发生高温、强非线性塑性变形的过程。经典内弹道学将弹丸简化成质点，忽略挤进过程，认为当火药气体压力达到某给定值时弹丸开始运动，模型带来的弹丸膛内运动误差通过次要功计算系数来修正，但无法获得刚体弹丸膛内运动的初始状态。由于弹带挤进终了的弹丸运动状态为弹丸在全深膛线内运动的初始状态，该初始状态直接影响弹丸膛内运动规律，从而影响弹丸飞离炮口的运动状态，因此研究弹带挤进机理及其运动规律具有重要科学意义。文献[1-2]采用有限元法和解析法研究了弹塑性弹带与身管间的相互作用规律，并进行了试验验证，认为弹带的结构形式对身管的承载影响最大，但整个计算模型中没有考虑温度的影响。文献[3]通过对发射后弹带硬度及组织演变规律的研究，认为弹带挤进后具有明显的层状特征，硬度最低的表层纤维组织因剧烈摩擦而迅速升温并导致局部再结晶，但该文没有给出摩擦、温度与结晶的理论关系。文献[4]采用气体炮发射撞击杆撞击弹丸模拟弹丸挤进过程，实验表明弹带挤进速度和温度对弹带的挤进过程影响较大。文献[5]利用有限元方法对弹丸挤进过程进行了模拟计算，弹底压力由实验测量值换算得到，实验获得了挤进过程中最大火药气体压力超过200 MPa，计算得到的最大挤进阻力在6×105N左右，对应弹丸速度超过60 m/s，但模型中没有考虑摩擦热的影响。文献[6]考虑了挤进过程中弹丸的动态冲击效应，建立了挤进阻力计算模型，应用两相流内弹道模型计算考虑挤进过程的内弹道性能。

还有一些学者研究了弹丸装填不到位、弹炮间隙、药室结构等因素对挤进过程的影响规律。文献[7]将经典内弹道方程组的解作为力学边界引入弹丸挤进有限元仿真过程，考虑塑性弹带材料损伤退化，对两种坡膛结构下的内弹道特性进行了研究。文献[8]对初始装填角、弹炮间隙以及装填不到位情况下的4种挤进过程进行了有限元与光滑粒子法耦合计算，结果认为弹炮间隙增大以及装填不到位会导致弹丸挤进速度变大。文献[9]建立了弹丸- 身管耦合系统非线性有限元模型，对大口径火炮挤进过程进行了模拟，认为弹丸装填状态的不一致导致身管阳线受力过大，是阳线起始段出现损伤现象的主要原因。

上述研究工作均没有考虑弹带挤进过程中起始内弹道、摩擦热、材料弹塑性等相互影响的热力耦合问题。为了比较准确地考虑挤进过程中各种物理现象对挤进过程的影响，本文通过考虑起始内弹道学、弹带弹塑性动力学、高温高压高速摩擦等物理状态相互耦合的影响，建立了弹带热力耦合挤进数学模型，对弹炮间隙、卡膛速度、初始卡膛姿态等使用条件对挤进过程的影响进行数值模拟分析，获得了相关因素对挤进阻力、弹丸运动规律等的影响。

1　弹带热力耦合挤进模型

1.1模型离散化

以某155 mm大口径榴弹炮为研究对象，从完整的身管上取出包含有药室和坡膛段(含有全深膛线)部分身管结构，分别建立该部分结构和弹丸弹带的三维8节点六面体实体网格模型，有限元网格准确刻画出了坡膛、阳线、阴线、弹带等关键部位的几何细节，以确保这些部位在卡膛与挤进过程中对力学性能的准确描述，整个模型包含有2 535 168个单元，如图1所示。在建立模型过程时考虑以下基本假设：

1)忽略弹丸与身管的变形，将其作为刚体考虑；

2)忽略身管后坐过程；

3)将炸药质量等效到弹体上。

图1　挤进过程有限元网格Fig.1　Finite element model of engraving process

1.2动力学与瞬态热传导模型

有限元离散化后弹塑性动力学模型[10]：

(1)

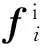
有限元离散化后瞬态热传导模型[10]：

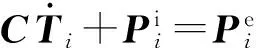
(2)

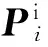
1.3挤进时期内弹道模型

以膛底圆心为原点，身管轴线指向炮口方向为x轴正向，针对挤进过程内弹道做如下假设：

1)假设药室形状为圆台，其母线为直线方程：

r=-kcx+r0，

(3)

式中：-kc为斜率；r0为膛底药室半径；x为距药室底部距离。

2)弹后火药气体速度线性分布。根据弹后火药气体速度线性分布的假设，可得弹后火药气体速度分布为

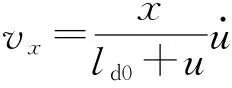
(4)

式中：vx为火药气体微元的速度；ld0为弹带卡膛到位后，弹带与坡膛闭气处至膛底的距离；u为弹丸沿着身管轴线的位移。

弹后火药气体压力分布为

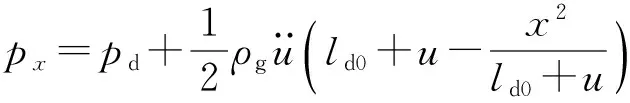
(5)

式中:pd为弹底压力；ρg为火药气体密度。(5)式表明px与弹带挤进位移u有关。

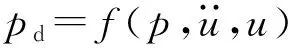
(6)

式中：Ax为距离药室底部x的药室截面积；Vu为弹丸前进距离u后，弹丸后部药室体积。Ax、Vu均是位移u的函数。

对经典内弹道方程进行改造，弹丸运动参数u等从有限元计算中提取，则挤进时期的内弹道气体压力方程可以写为

(7)

式中：fp为火药力；ω为装药量；ψ为火药相对燃烧量；θ为热力指数；As为炮膛横截面积；lψ为药室自由容积缩径长，lψ=l0[1-Δ(1-ψ)/ρp-αΔψ]，l0=Vu/Au为药室容积缩径长，Au为距离药室底部u+ld0处的横截面积，Δ为装填密度，ρp为火药固体密度，α为余容；E为火药燃气对外做功。

则内弹道求解方程可以写为

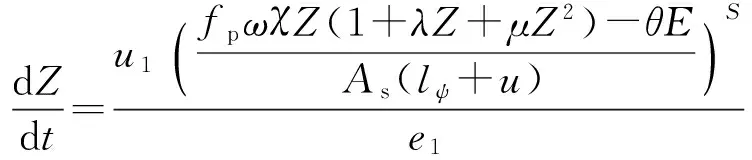
(8)

式中：u1为燃速系数；S为压力指数；Z为火药相对燃烧厚度；e1为火药厚度；χ、λ、μ均为火药形状特征量。由于(8)式中耦合了弹带的挤进位移u，相对于经典内弹道模型，该式也称为内弹道耦合模型。

由于在弹丸起始运动过程中后坐位移较小，因此忽略后坐消耗的能量，火药燃气对外做功可写为

E=Ek+Ef+Es+Eg,

(9)

式中：Ek、Ef、Es、Eg分别为弹丸动能、摩擦耗散能、弹塑性应变能以及火药气体运动能，前3项可以从有限元求解过程中获得，Eg采用经典内弹道中的计算方程获得。对(8)式采用4阶龙格- 库塔方法进行求解，初始值设为点火药燃烧后药室内火药气体压力。

1.4摩擦模型

对高速摩擦过程的研究成果表明，如果表面接触压力较大且相对滑动速度较快，经典库伦摩擦定律会得到较大的误差[12-14]。在高速切削以及摩擦搅拌焊接过程中，工件之间接触压力可达吉帕量级，相对滑动速度可达几十米每秒，在对上述两种高速高压摩擦现象进行计算时多采用改进的库伦摩擦模型，切应力ft为

(10)

式中：μ为摩擦系数；σn为接触面的正压力；τs为材料的许用切应力，取为

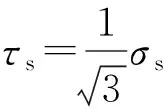
(11)

σs为材料的许用拉应力。

文献[15-17]认为在高速滑动过程中，拥有较低熔点的金属材料容易形成局部剪切现象，温度对表面材料的力学特性起到主导作用。Baig等[18]以及Lennon等[19]发现纯铜材料在大应变下的应变率强化效应不明显，且在高温下材料的应变强化与应变率强化效应均已减弱。Puls等[20]采用前角极小的刀具对高速切削进行实验研究，观察到刀具与工件接触面上有半熔化的材料被挤出，其认为材料热软化是造成高速摩擦过程摩擦系数不断降低的主要原因，并且提出如下模型来计算摩擦系数：

(12)

式中：Tm为弹带材料熔点温度；m为温度影响项参数；μs为滑动摩擦系数；T为弹带温度；Td为摩擦状态转换温度。参数μs、Td、m通过对比实验与数值模拟结果得到。上述研究均说明在高速高压摩擦过程中，接触面上温度上升导致的热软化对材料力学性能起到了主导作用。因此假设挤进过程中，仅有温度对接触表面材料力学性能起到影响作用，借鉴(12)式，只考虑Johnson-Cook材料本构模型中的温度影响项，将材料的许用切应力表示为

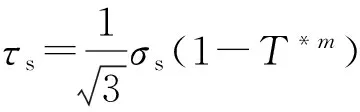
(13)

式中：T*=(T-Tr)/(Tm-Tr)，Tr为环境温度。将(11)式与(13)式带入(10)式得到了新的摩擦模型。

1.5弹丸姿态表示方式

弹体坐标系Ocξηζ由弹丸质心平动坐标系Ocx0y0z0按照3-2-1(绕着Ocz0旋转，再绕着Ocy0旋转，最后绕着Ocx0旋转)旋转φ1、-φ2、γ3个欧拉角得到[21]。在坐标系Ocx0y0z0中，Ocx0轴沿着身管轴线指向炮口，Ocy0轴沿着垂向向上，φ1、-φ2分别为弹丸纵向摆角和横向摆角，φ10、φ20分别表示在卡膛前的弹丸初始摆角，φ11、φ21分别表示挤进完成时的弹丸摆角。

1.6热力耦合模型的计算

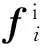
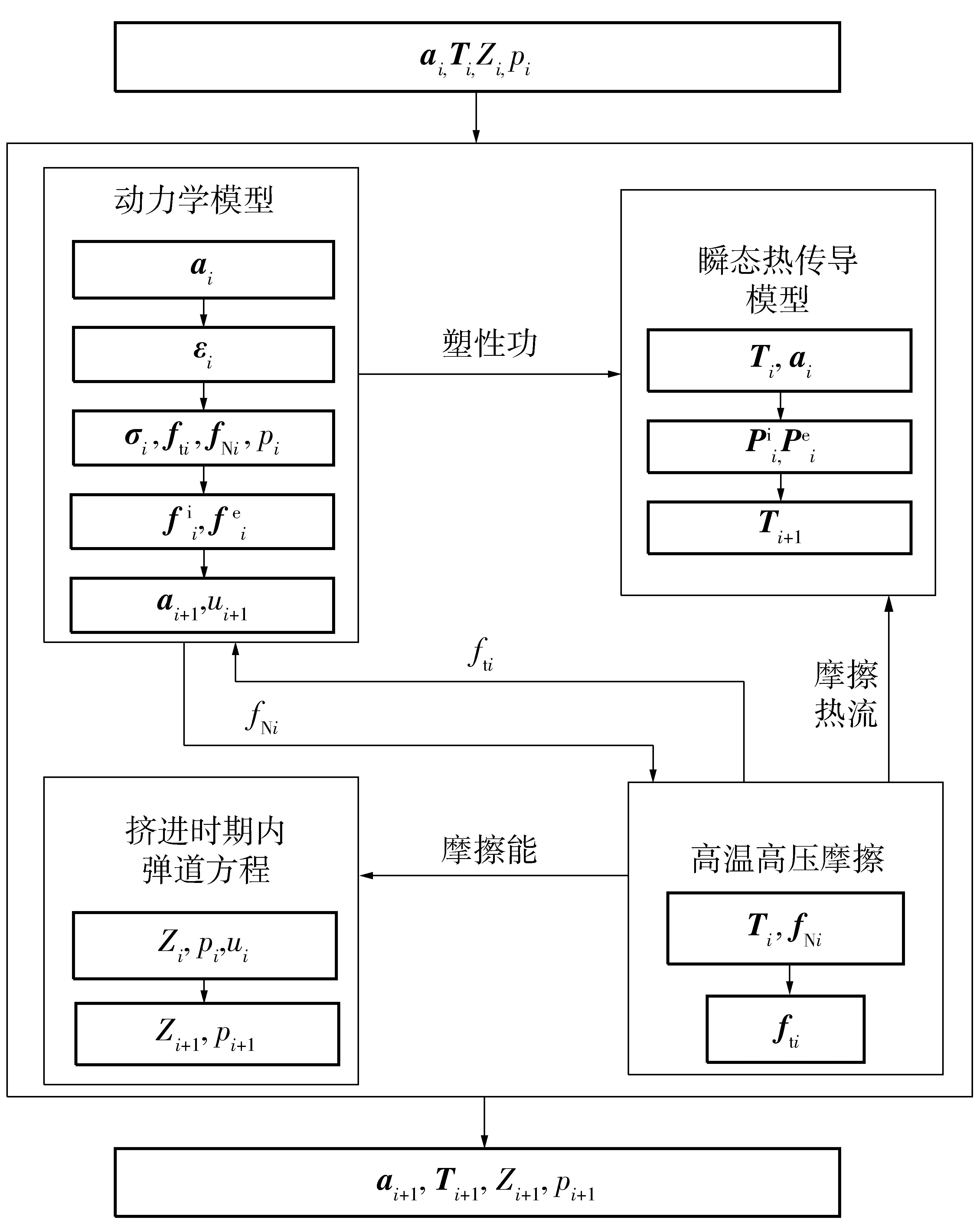
图2　耦合计算流程Fig.2　Flowchart of coupled analysis

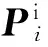
将所建立的有限元模型利用ABAQUS软件的显式动力学模块进行求解，采用减缩积分单元，可以有效控制计算成本和模拟大变形过程。利用VUAMP以及VFRICTION子程序接口来实现内弹道程序，摩擦模型与动力学方程以及瞬态热传导模型的耦合计算。

2　计算过程描述

击发底火前，输弹机输弹、弹丸获得一定卡膛速度，并以初始卡膛姿态强迫弹带卡膛，弹带材料与身管坡膛发生碰撞产生塑性变形和残余应力，弹丸依靠弹带残余应力和摩擦力稳定卡在坡膛上。挤进初始条件由弹带卡膛结束时的姿态决定，因此挤进过程之前应首先计算卡膛过程。卡膛过程离散化模型与挤进过程模型一致，给定弹丸质量、卡膛速度和初始摆角以模拟弹丸惯性卡膛。待弹丸稳定卡膛之后，再施加弹底压力边界条件模拟挤进过程。在挤进结果处理中，提取的挤进阻力f是指在弹带挤进坡膛和膛线过程中，坡膛和膛线对弹带作用引起的法向载荷和切向摩擦力在身管轴线方向的分量。挤进过程中弹丸状态参数包括弹丸质心轴向位移u、速度v、摆角φ1和φ2，此外还包括火药气体平均压力p、挤进阻力f、弹带温度T等。

3　弹带挤进过程数值模拟

在以下的计算中除特别说明外所用的模型均为本文前面提出的热力耦合挤进模型，假定弹丸以3 m/s的速度正卡膛，弹丸质量45.5 kg，弹炮间隙取为0.55 mm，每个算例均与常用经典模型进行比对。

3.1内弹道耦合作用

图3给出了热力耦合挤进模型和经典内弹道模型计算得到的弹带挤进规律。由图3可见由经典内弹道挤进模型计算得到的火药气体平均压力p、弹丸速度v均比耦合模型的结果要大，且挤进时间短、挤进结束时膛压高。其原因是在挤进过程中，弹带变形能和摩擦耗散功是巨大的，采用经典内弹道学中次要功系数方法得到的火药燃气对外做功较小，使得内弹道能量平衡方程中火药气体势能大，导致在经典内弹道挤进模型中火药气体压力大。两种模型计算得到的挤进阻力差别不大、均在106N量级，说明挤进速度对挤进阻力影响不大。图3中还表明，挤进结束时弹丸运动速度已达90 m/s、火药气体平均压力达到200 MPa的量级；此压力与经典内弹道中给定30 MPa的量级完全不同，这一结论与文献[5]中的实验结果相吻合。

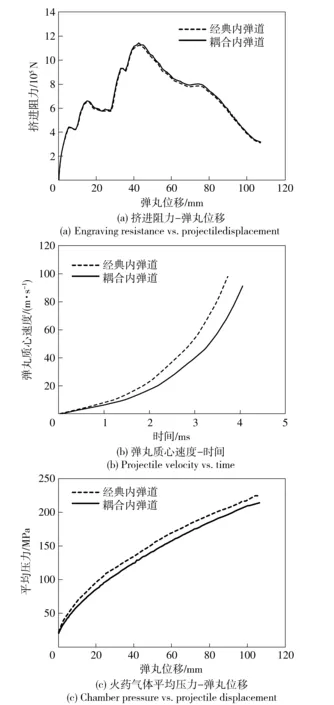
图3　内弹道耦合/经典内弹道挤进过程计算结果Fig.3　　　　Comparison of calculated results of coupled and uncoupled internal ballistic engraving processes

3.2热力耦合作用

图4显示了挤进前后弹带的外形变化，其中前后弹带分别有一横槽以承受弹带材料向后的流动。图5显示了本文建立的热力耦合模型与经典绝热挤进模型计算得到的挤进结束时弹带表面温度分布，图中横坐标原点为弹带与身管阳线或阴线靠近炮口方向的接触点，方向指向炮尾，如图4(c)中所示。由图5可见，在热力耦合挤进过程中，由于考虑了摩擦热和弹带材料塑性变形热，弹带表面温度达到1 200 K以上，接近材料熔点温度，表明弹带材料性能在挤进结束时已发生剧烈变化；而在绝热挤进过程中，弹带表面温度在500 K以下，表明弹带材料性能在挤进结束时变化不大。图5中出现波谷及波谷位置不同的原因是由于前后弹带存在横槽且几何结构不同引起。两种模型计算得到的温度差异所引起材料性能的变化必然导致如图6所示的不同挤进结果，从图6中可以看出，绝热挤进模型计算得到的挤进阻力和火药气体平均压力明显大于热力耦合模型的值、挤进速度小于热力耦合模型的值。

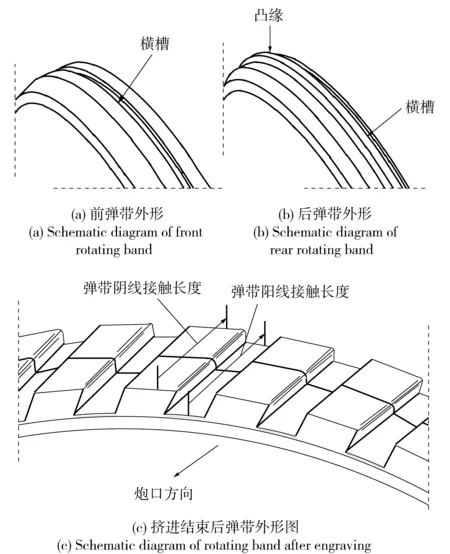
图4　挤进前后弹带外形Fig.4　　　　Schematic diagram of rotating band before and after engraving

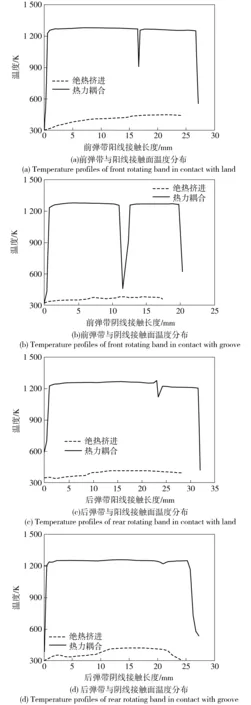
图5　挤进完成后弹带表面温度分布Fig.5　　　　Temperature profiles of rotating band at the end of engraving

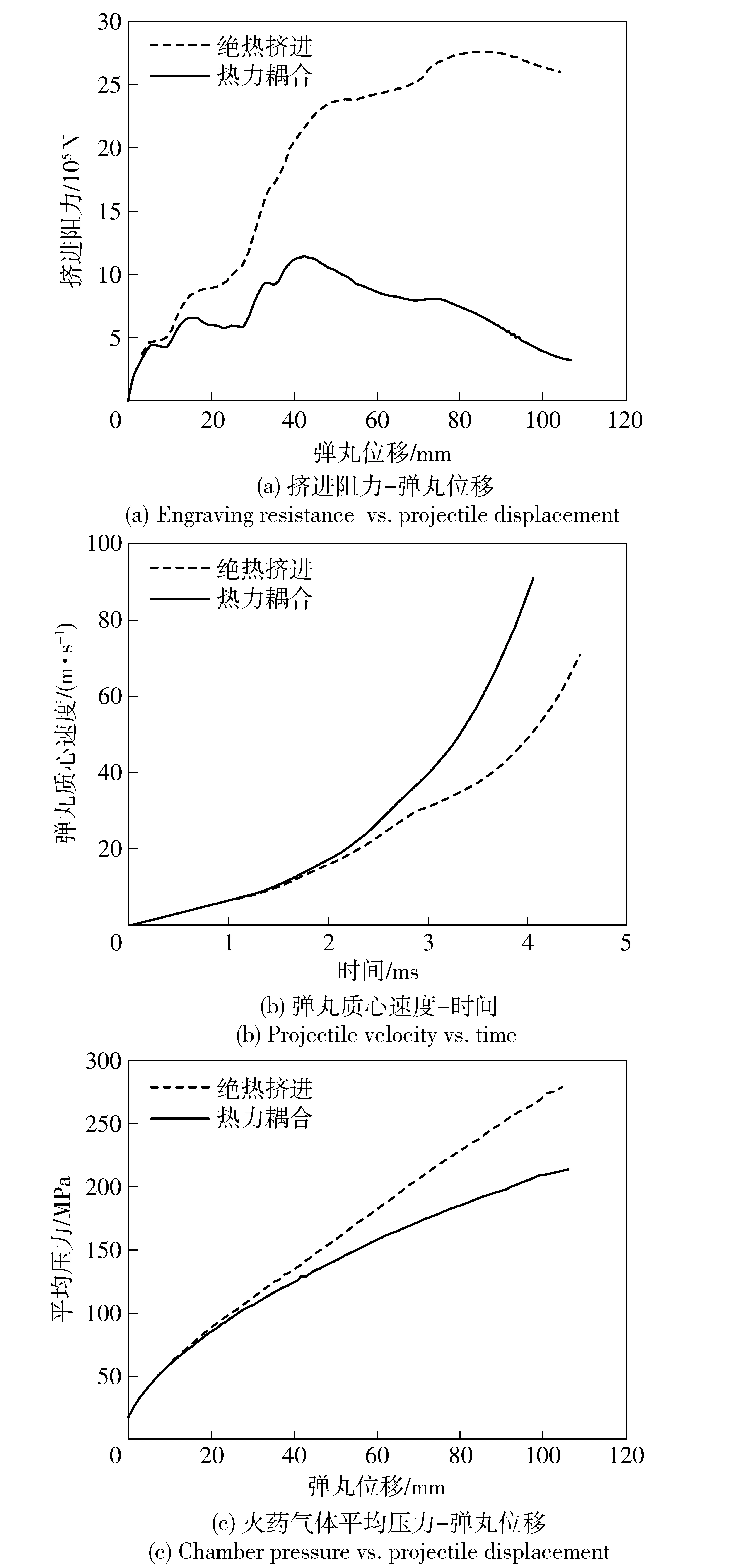
图6　绝热/热力耦合挤进过程计算结果Fig.6　Comparison of results between adiabatic and coupled thermo-mechanical analyses of engraving process

4　弹带挤进规律

弹丸前定心部与身管阳线的半径差为弹炮间隙，火炮在发射一定数量的弹丸之后弹炮间隙、卡膛速度、弹丸初始摆角等均会出现不同程度的变化，导致卡膛规律的变化，继而影响挤进过程中的弹带受力变形以及弹丸运动规律。

4.1弹炮间隙的影响

考虑身管报废时的内膛磨损量以及新身管内膛与弹丸定心部的公差，取弹炮间隙的上、下限为0.80 mm以及0.05 mm，并考虑弹炮间隙的均匀分布，对弹炮间隙分别为0.05 mm、0.30 mm、0.55 mm及0.80 mm的情况进行计算，得到f、v、p的变化规律，如图7所示。由图7可见，随着弹炮间隙的增大，挤进时间减小、挤进阻力减小、弹丸速度增大、火药气体平均压力变小，但不同弹炮间隙下的挤进阻力的变化规律保持一致。

图7　　　　不同弹炮间隙下挤进阻力、弹丸速度与平均压力的变化Fig.7　Engraving resistance, projectile velocity and propellant gas pressure in the case of different barrel-projectile clearances

表1列出了不同弹炮间隙下最大挤进阻力fmax、挤进完成时的弹丸摆角φ11、φ21的数值。由表1可见，弹炮间隙为0.80 mm时的fmax比弹炮间隙为0.05 mm时减小1/3左右；随着弹炮间隙的增大，φ11的绝对值也逐渐变大，且最终呈现“低头”姿态，φ11的数值比φ21大1个数量级。特别要注意的是，随着间隙的增加，挤进结束时弹丸速度由88.23 m/s增加到91.84 m/s，间隙是导致弹丸初速误差增大的一个重要原因。

4.2卡膛速度的影响

不同卡膛速度会导致不同的卡膛深度以及弹带上不同的残余应力，使得挤进过程中弹丸运动克服的阻力不同和起始内弹道过程不同。表2给出了弹炮间隙为0.55 mm，卡膛速度分别为2.0 m/s、2.5 m/s以及3.0 m/s时的计算结果。可见当卡膛速度增大，最大挤进阻力fmax、挤进完成时火药气体最大平均压力pmax和弹丸摆角均变化不大，但弹丸质心最大速度vmax提高了1 m/s. 这表明卡膛速度对其他参数影响不大，但会影响挤进结束时的弹丸速度。

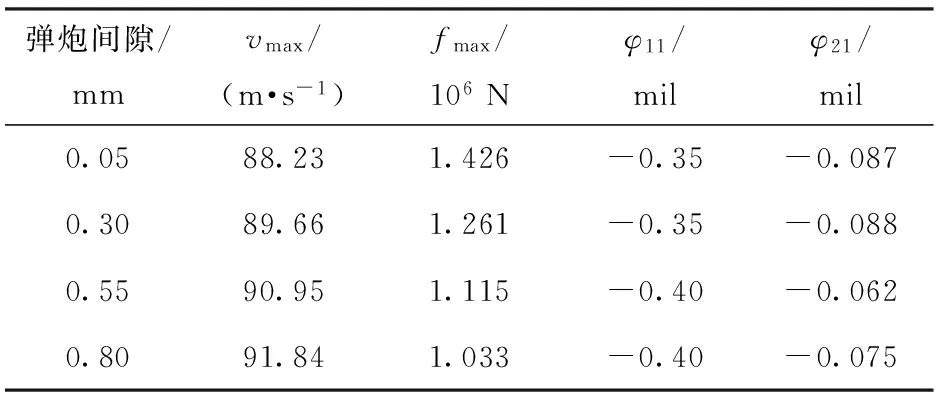
表1　　　　不同弹炮间隙下的最大挤进阻力以及挤进完成后的弹丸摆角

表2　卡膛速度对挤进速度和火药气体压力的影响

4.3弹丸初始摆角的影响

假定弹丸以初始纵向摆角φ10和横向摆角φ20进行卡膛，弹炮间隙为0.55 mm，卡膛速度3.0 m/s，初始纵向摆角φ10分别为±2 mil、±1 mil，初始横向摆角φ20分别为2 mil、1 mil，其中φ10对弹丸姿态的影响如图8所示。注意图8中横坐标原点对应的值为卡膛终了弹丸纵向摆角即弹丸挤进初始纵向摆角，该摆角由卡膛过程的弹塑性有限元计算得到，由于弹丸重力的作用，无论φ10正负与否，卡膛结束时弹丸纵向摆角永远为负。

图8　不同的φ10对φ1的影响Fig.8　Effect of φ10 on φ1

由图8可见，若φ10>0 mil，即弹丸卡膛前处于“抬头”状态，在挤进过程以及最终挤进完成后的弹丸姿态较好，且“抬头”角度越大挤进过程中φ1绝对值越小。表3给出了φ10对挤进速度和火药气体压力的影响。由表3中可见，当φ10减少时，挤进阻力、火药气体平均压力变大，挤进速度变小。计算表明φ20对挤进阻力、火药气体平均压力、挤进速度以及弹丸姿态变化影响不大。

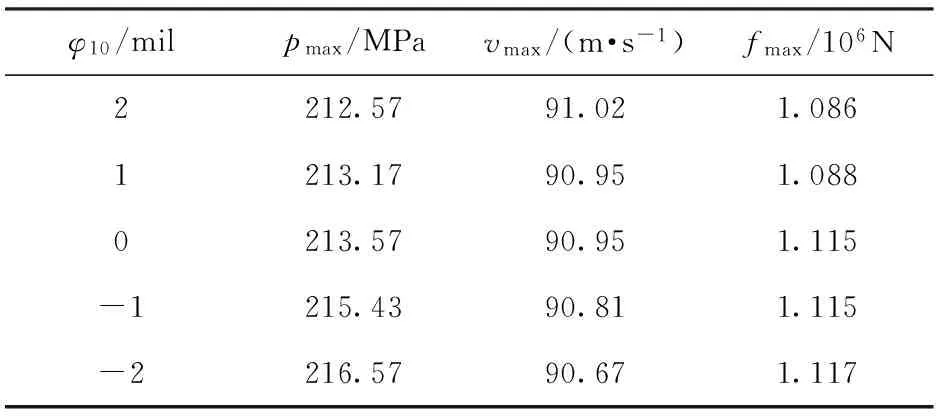
表3　φ10对挤进速度和火药气体压力的影响

5　结论

本文综合考虑挤进时期内弹道学模型，温度退化摩擦模型，挤进过程弹塑性动力学模型以及瞬态热传导模型，建立了弹带热力耦合挤进模型，对大口径火炮挤进过程进行了数值模拟，对非耦合模型与热力耦合模型之间的计算结果进行了对比，验证了热力耦合计算的必要性。计算结果表明，挤进过程结束时，弹丸速度可达90 m/s左右，火药气体的平均压力可达200 MPa左右，挤进过程中身管对弹带的阻力达到106N量级。

考虑弹炮间隙、卡膛速度以及初始摆角的变化对挤进过程进行了计算，总结如下：

1) 弹炮间隙直接影响挤进结束时弹丸姿态和速度，也是弹丸初速误差产生的重要因素。计算表明，随着弹炮间隙的增加，挤进阻力明显减小，挤进过程中弹丸速度增大，火药气体平均压力减小。

2)卡膛速度对挤进过程影响较小，因此在决定卡膛速度时应以卡膛稳定为基本原则。

3)初始纵向摆角φ10是影响挤进结束时弹丸姿态的主要因素，确保弹丸保持“抬头”卡膛姿态会使弹丸在挤进结束时具有较好的姿态，φ20对挤进结束时弹丸姿态影响较小。

References)

[1]Keinänen H, Moilanen S, Tervokoski J, et al. Influence of rotating band construction on gun tube loading-part I: numerical approach[J]. Journal of Pressure Vessel Technology, 2012, 134(4):041006.

[2]Toivola S, Moilanen S, Tervokoski J, et al. Influence of rotating band construction on gun tube loading-part II: measurement and analysis[J]. Journal of Pressure Vessel Technology, 2012, 134(4):041007.

[3]殷军辉, 郑坚, 倪新华, 等. 弹丸膛内运动过程中弹带塑性变形的宏观与微观机理研究[J]. 兵工学报, 2012, 33(6): 676-681.

YIN Jun-hui, ZHENG Jian, NI Xin-hua, et al. Research on macroscopic and microscopic mechanism of plastic deformation of bearing band[J]. Acta Armamentarii, 2012, 33(6): 676-681.(in Chinese)

[4]Wu B, Zheng J, Tian Q, et al. Friction and wear between rotating band and gun barrel during engraving process[J]. Wear, 2014, 318(1/2): 106-113.

[5]孙全兆, 杨国来, 王鹏, 等. 某大口径榴弹炮弹带挤进过程数值模拟研究[J]. 兵工学报, 2015, 36(2):206-213.

SUN Quan-zhao, YANG Guo-lai, WANG Peng, et al. Numerical research on rotating band engraving process of a large-caliber howitzer[J]. Acta Armamentraii, 2015, 36(2): 206-213.(in Chinese)

[6]邱从礼, 侯日升, 赵锋, 等. 考虑弹丸动态冲击条件下的内弹道性能研究[J]. 弹箭与制导学报, 2014, 34(4)： 140-142.

QIU Cong-li, HOU Ri-sheng, ZHAO Feng, et al. Interior ballistics performance of guns considering dynamic impact of projectile[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(4): 140-142.(in Chinese)

[7]孙河洋, 马吉胜, 李伟, 等. 坡膛结构变化对火炮内弹道性能影响的研究[J]. 兵工学报, 2012, 33(6): 669-675.

SUN He-yang, MA Ji-sheng, LI Wei, et al. Study on influence of bore structure on gun’s interior ballistic performances[J]. Acta Armamentraii, 2012, 33(6): 669-675.(in Chinese)

[8]马明迪, 崔万善, 曾志银, 等. 有限元与光滑粒子耦合的弹丸挤进过程分析[J]. 振动与冲击, 2015, 34(6)：146-150.

MA Ming-di, CUI Wan-shan, ZENG Zhi-yin, et al. Engraving process analysis of projectiles based on coupling of FEM and SPH[J]. Journal of Vibration and Shock, 2015, 34(6): 146-150.(in Chinese)

[9]曾志银, 马明迪, 宁变芳, 等. 火炮身管阳线损伤机理分析[J]. 兵工学报, 2014, 35(11):1736-1742.

ZENG Zhi-yin, MA Ming-di, NING Bian-fang, et al. Analysis of rifling land damage mechanism of gun barrel[J]. Acta Armamentarii, 2014, 35(11): 1736-1742.(in Chinese)

[10]Dassault Systèmes Simulia Corp.ABAQUS theory manual[M]. Providence, RI, US:Dassault Systèmes Simulia Corp, 2013.

[11]Johnson G, Cook W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C]∥7th International Symposium on Ballistics. Hague,Netherlands:IBS, 1983: 541-547.

[12]郭建英. 基于不同刀- 屑摩擦模型的金属切削过程动力学研究[D]. 太原:太原理工大学, 2010.

GUO Jian-ying. Study on metal cutting dynamics based on different tool-chip friction models[D].Taiyuan:Taiyuan University of Technology, 2010.(in Chinese)

[13]Tiernan P, Hillery M T, Draganescu B, et al. Modeling of cold extrusion with experimental verification Friction and wear mechanism at high sliding speeds[J]. Journal of Materials Processing Technology, 2005, 168: 360-366.

[14]Grujicic M, He T, Arakere G, et al. Fully coupled thermomechanical finite element analysis of material evolution during friction-stir welding of AA5083[J]. Journal of Engineering Manufacture, 2010, 224(4): 609-625.

[15]Batra R, Kim C. Effect of viscoplastic flow rules on the initiation and growth of shear bands at high strain rates[J]. Journal of Mechanics and Physics of Solids, 1990, 38(6): 859-874.

[16]Batra R, Wei Z. Shear bands due to heat flux prescribed at boundaries[J]. International Journal of Plasticity, 2006, 22(22): 11-15.

[17]Wei Z G, Batra R. Modeling and simulation of high speed sliding[J]. International Journal of Impact Engineering, 2010, 37(12): 1197-1206.

[18]Baig M, Khan A, Choi S, et al. Shear and multiaxial responses of oxygen free high conductivity (OFHC)copper over wide range of strain-rates and temperatures and constitutive modeling[J]. International Journal of Plasticity, 2013, 40(1): 65-80.

[19]Lennon A, Ramesh K. The influence of crystal structure on the dynamic behavior of materials at high temperatures[J]. International Journal of Plasticity, 2004, 20(2): 269-290.

[20]Puls H, Klocke F, Lung D. Experimental investigation on friction under metal cutting conditions[J]. Wear, 2014, 310(1/2): 63-71.

[21]李淼, 钱林方, 陈龙淼, 等. 弹丸卡膛规律影响因素分析[J]. 兵工学报, 2014, 35(8): 1152-1157.

LI Miao, QIAN Lin-fang, CHEN Long-miao, et al. Analysis of influence factors of projectile band bayonet-chamber process[J]. Acta Armamentraii, 2014, 35(8): 1152-1157.(in Chinese)

Research on Coupled Thermo-mechanical Model During Rotating Band Engraving Process

LI Miao1， QIAN Lin-fang1， SUN He-yang2

(1.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China; 2.Department of Artillery Engineering, Ordnance Engineering College, Shijiazhuang 050003, Hebei, China)

To investigate the mechanism of engraving process and the rule of initial motion of projectile during lauching process, the engraving process of rotating band of large-caliber howitzer is simulated. The gas pressure distribution of propellant in the tapered chamber is taken into consideration to get the interior ballistic equation during engraving process, and the solution of the equation is taken as the boundary condition of coupled thermo-mechanical analysis of engraving process. Meanwhile, the friction between the rotating band and the barrel is modeled using modified Coulomb model in which the temperature at the interface is taken into consideration. Uncoupled internal ballistic engraving process and adiabatic engraving process are calculated to verify the necessity of the coupled analysis. The resistance, projectile velocity, propellant gas pressure and projectile attitude are got by considering the changes in clearance between projectile and barrel, initial velocity and initial projectile attitude. The calculated results show that the clearance between projectile and barrel plays an important role in determining the resistance and projectile velocity, and the initial projectile attitude has a great effect on the projectile attitude in the process of engraving.

ordnance science and technology; coupled thermo-mechanical; engraving resistance; projectile attitude

2015-12-03

国家自然科学基金项目(11472137)

李淼(1988—)，男，博士研究生。E-mail: limitmiao@163.com；

钱林方(1961—)，男，教授，博士生导师。E-mail:lfqian@vip.163.com

TJ303

A

1000-1093(2016)10-1803-09

10.3969/j.issn.1000-1093.2016.10.006