基于谐波理论的轴孔特征误差分离与表面形貌预测

苏长青, 孙业翔, 屈力刚, 叶柏超, 杨野光

(沈阳航空航天大学 航空制造工艺数字化国防重点学科实验室， 辽宁 沈阳 110136)



基于谐波理论的轴孔特征误差分离与表面形貌预测

苏长青, 孙业翔, 屈力刚, 叶柏超, 杨野光

(沈阳航空航天大学 航空制造工艺数字化国防重点学科实验室， 辽宁 沈阳 110136)

轴孔零件作为机械产品中应用最为广泛的核心零件趋于向高精度、高强度、多元化方向发展，其质量控制和质量评价至关重要。针对轴孔零件的形位误差分离问题，在研究了传统的误差分离技术和谐波理论的基础上，提出了轴孔零件形位误差的谐波分离方法。根据在零件上测得的周期性数据，分析了各次谐波误差的产生机理，提出了控制低次谐波误差的措施。利用空间点矢量法获得了测量点实际位置，结合拟合算法对零件表面形貌进行了预测。通过实验验证了形位误差谐波分离和表面形貌预测方法的准确性和合理性，为轴孔零件的表面质量评价和预测提供一种新的思路。

机械制造工艺与设备； 误差分析； 谐波测量； 形貌预测； 谐波理论； 误差分离

0　引言

作为在机械类产品中最为常见的轴孔类零件、零件中的轴孔类特征常常作为产品中的核心零部件、关键特征来使用，在国防军工、航空航天、船舶制造、汽车工业等领域得到了广泛的应用。轴孔类零件产品在制造及应用的过程中，其加工质量将直接决定零件在使用过程中的安全性、准确性和工作效率。在检测轴孔特征时，圆度、圆柱度、径向跳动和端面跳动是评价轴孔特征加工质量的4个非常重要的技术参数[1-3]。

由于轴孔类零件在检测时对径向和轴向的检测要求不同，所以检测的方式也各有差别。目前，在检测零件轴孔特征时，最常用的方法是坐标测量法和点云分析法[4-5]。通过接触式测量或非接触式测量的方式来获得特征表面的实际位置信息，根据轴孔特征形位公差的评价算法拟合被测特征实际轮廓，并据此得到被测特征的形位误差[6-7]。由于工艺系统会存在系统误差，因此零件在加工过程中会产生偏心误差，对零件的加工精度造成一定影响[8]。为了将零件截面圆圆心与回转中心不重合而产生的偏心误差分离出来，利用误差分离技术(EST)分离形位误差中的偏心误差，进而得到经过校正的形位误差[9-10]。利用EST可准确地获得被测特征的轮廓信息，剔除了由于装夹、制造偏心所产生的影响，操作简便、测量效率高，可较快得出质量评价结果。但EST分离偏心误差的过程需要大量测量数据来保证其准确性，且分离算法较为复杂，对零件的测量效率会产生一定影响[11-12]。零件表面质量的高低也会对零件的使用寿命、使用效率和使用安全造成一定影响。为了降低零件的过程误差，提高零件的加工质量和加工效率，需要对零件进行中间检测和表面质量预测，以改善零件的工艺过程，优化零件的结构和检测方法[13-14]。

针对轴孔类零件误差分析与表面质量预测的问题，在研究了EST和谐波分析法基本原理的基础上，提出了零件形位误差的谐波分离方法。通过对测得的周期性数据进行傅里叶变换来求解被测特征的各次谐波误差并给出其物理意义，据此完成对被测特征的评价。根据被测特征的特点，结合空间点矢量法，通过对零件表面形貌的预测来完成表面质量的控制。

1　轴孔零件的误差来源

图1　零件复映误差示意图Fig.1　　　　Schematic diagram of mismachining tolerances of shaft parts

零件在加工过程中会产生热变形即切削热。切削热也是影响零件加工质量的因素之一，在高精密加工中由切削热引起的误差难以修复。影响切削热的因素较多，且具有一定随机性，因此零件热变形问题很难处理。同时，切削力及切削力的变化会引起零件变形，这些影响因素都会复映在零件上，从而影响零件的加工质量[16]。

零件的加工质量对零件的使用寿命、工作效率、疲劳强度、使用安全及可靠性都会产生影响，因此，在加工时应尽量保证工艺系统的稳定性以降低零件的随机误差。

2　轴孔零件形状误差谐波分离原理

零件的轴孔类特征有很多检测手段，如光学非接触式检测设备、光学扫描仪、量块、圆度仪、三坐标测量机(CMM)等检测设备。在使用CMM对零件的轴孔类特征检测时，测头传感器中记录的是测针在被测特征上所分布的一圈测量点实际位置的数据，同时，由于测量点在被测特征的圆周上按照均匀方式分布，故在测量被测特征一圈时所收集的测量点数可看作是一组周期信号。一组周期信号作为输入的周期函数可对其进行傅里叶变换，分解为由一组正弦波信号作为输出周期函数的集合，亦可通过傅里叶变换将一组正弦信号叠加成一个非正弦周期函数。由测得的周期性信号进行傅里叶变换后分解出的各阶正弦曲线即为谐波[17-18]。

设f(x)为非正弦周期函数，频率与角频率分别为f和ω，且满足狄里赫利条件，则可将f(x)展开成傅里叶级数

f(x)=A0+A1sin(x+φ1)+A2sin (2x+φ2)+…+

Aisin (ix+φi)+…=

(1)

式中：n=1,2,3,…；A0称为直流分量，其余各项为具有不同振幅，不同初相且频率都为整数的正弦分量；A1sin (x+φ1)称为基波，A1、φ1分别为其振幅和初相；A2sin (2x+φ2)称为2次谐波，其特点是频率为基波频率的2倍，A2和φ2分别为其振幅和初相；根据各分量频率与基波频率的关系，可得3次谐波、4次谐波、5次谐波等。(1)式亦可表示为

(2)

对于普通的周期函数而言，ai和bi可通过积分的方法求得，如(3)式所示。

(3)

式中：n=1,2,3，….

在检测轴类零件时，需要对其圆度、圆柱度、径向跳动等形位误差进行评价，从而综合评价零件质量。然而，在大多数情况下，确定周期的函数是未知的，但可以获得函数上一些离散点的数据，利用这些离散的坐标数据求解各次谐波。

取(3)式中的前2n+1项代入(2)式中即可得到第n次谐波，这种方法称为离散点坐标法。根据测量点坐标值、傅里叶因数、实际测量值之间的关系，可建立关系矩阵来求解傅里叶因数，即

AF=Y，

(4)

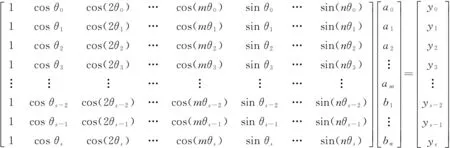
式中：A为系数矩阵；F为傅里叶因数；Y为实际测量值。

当A为方阵时，将等式两边同时乘A-1，可得到傅里叶因数求解公式，即

A-1AF=A-1Y，

F=A-1Y.

(5)

当A不为方阵时，可将F看作AF=Y的解向量，通过求解A的广义逆矩阵A(1)来求解F，即

F=A(1)Y+(E-A(1)A)b，b∈Cn，

(6)

式中：E为单位矩阵；b为n维复向量空间任意列向量；Cn为n维复向量空间。

将所求得的傅里叶因数代入(2)式，即可获得各次谐波的表达式和各次谐波的振幅、相位等相关参数。根据所分离出来的各次谐波误差即完成对轴孔零件形状误差的谐波分离。

3　轴孔零件表面形貌分析与预测

测量及分析被测零件的谐波误差对评价与控制零件的加工质量和改进零件的工艺过程都起到了至关重要的作用。谐波误差是由检测设备、测量方式、工艺过程、零件材料、现场环境等因素共同作用而产生的复合形式的误差。

通常各次谐波误差形成的机理也各不相同。1次谐波误差，零件相对于回转主轴的偏心程度，即零件的偏心误差，偏心量通过重新装夹找正被消除。2次谐波误差，由于偏心等定位不准确所造成的零件椭圆形误差，即径向椭圆形误差。3次谐波误差，由于制造过程中，定位方法、工装夹具及刀具选择不当造成的误差，即制造因素误差。4次谐波误差，零件工艺过程不当，零件由于热处理工艺不当以及加工时产生的热变形而造成零件弹性变形都是造成四次谐波的主要原因，即工艺因素误差。5次谐波误差，由制造现场环境的稳定程度所引起的误差，如加工现场温度、湿度、振动、润滑剂等都将对零件质量产生一些细微的影响，即环境因素误差。5次以上谐波误差称为高次谐波误差，即零件加工时所产生的高次微观误差。与前几次谐波误差相比，高次谐波误差对零件的影响可忽略，各次谐波如图2所示。

图2　2～5次谐波示意图Fig.2　Schematic diagram of harmonics

在利用谐波分析法对零件进行误差分析时，可根据特征的测量点分布原则分布测量点，测得零件表面的坐标数据后，根据傅里叶变换将其展开为傅氏级数，进而获得各次谐波误差。在可忽略高阶谐波误差的条件下或以高阶谐波误差作为替代误差，用主要影响零件质量的低阶谐波误差来代替零件的加工误差。根据谐波误差的物理意义和产生机理，分析零件误差的来源，优化设计、工艺及检测过程，进而降低零件误差，如图3所示。

图3　零件误差分析Fig.3　Error analysis of shaft and hole parts

为了获得零件加工后表面的实际形貌，可由空间点矢量法来计算零件上某点在空间中的实际位置。根据被测零件表面各点的实际位置来预测零件的表面实际形貌，如图4所示。

空间点矢量法的基本原理是坐标测量法，通过测量设备可识别的中性测量程序(标准DMIS程序)驱动测量机按照既定的测量路线，在被测零件表面上精确地测得点在空间坐标(x,y,z)和矢量(i,j,k)的数值，将测量数据在计算机中处理，拟合被测特征的实际轮廓[19]。

由空间点矢量法可获得测量点的实际位置，即

T=Δxi+Δyj+Δzk，

(7)

式中：T为测量点实际位置与理论位置的偏离程度；当T>0时，测量点实际位置在理论位置之上；当T<0时，测量点实际位置在理论位置之下；Δx=xm-xt，Δy=ym-yt，Δz=zm-zt,xm、ym、zm为实测值，xt、yt、zt为理论值；i、j、k分别为X、Y、Z的方向矢量。

根据测量点在零件表面上的分布，通过空间点矢量法计算其实际位置，由所有通过空间矢量法计算得到的点拟合一个曲面，即为零件表面的预测形貌，如图4所示。零件表面的预测形貌可由矩阵表示为

S=ΔΛ,

(8)

图4　随机测量点阵Fig.4　Random measuring lattice

4　谐波测量与分析

图5　测量设备与待测零件Fig.5　Measuring equipment and parts under measuring

为了求解零件谐波误差，可把一个周期2π分成8、12、20、24、36、48等份，即取测量点数为4的整数倍，可分别得到1～4次谐波误差，1～6次谐波误差，1～10次谐波误差，1～12次谐波误差，1～18次谐波误差，1～24次谐波误差。为获得零件的前5次谐波误差，本文采用12点坐标法对零件的谐波进行测量，表1为零件应用12点法所获得的实测数据。

将表1中的测量数据代入(5)式中，即可求得傅里叶因数F=(a0,a1,a2,…,an,b1,b2,…,bn)T. 将所求得的傅里叶因数代入(2)式中，即可求得各次谐波幅值和相位，其中谐波幅值即为所求谐波误差，如表2所示。

由表2可知，零件的1～5次谐波误差分别为28.007 68 μm，5.861 08 μm，1.433 61 μm，2.059 51 μm，3.179 25 μm. 由此可得，零件装夹及切削振动造成的偏心误差为28.007 68 μm，偏心误差是可以通过重新装夹定位、更换刀具和切削参数等手段来消除。零件的2次谐波误差(椭圆形误差)为5.861 08 μm，可通过调整切削参数、定制专用工装等方法来减小。零件的3次谐波误差(制造因素误差)为1.433 61 μm，可适当改变夹持力、调整加工刀具及重新选择定位方式等方法来改善。零件的4次谐波误差(工艺因素误差)为2.059 51 μm，可适当改善工艺流程以减小切削时所产生内应力和热变形。零件的5次谐波误差(环境因素误差)为3.179 25 μm，在零件加工时，应尽量保持现场环境稳定，以减小环境因素对加工过程造成的影响。

表1　应用离散点坐标法(12点法)测得的零件数据

表2　1～5次谐波幅值

为了获得零件的综合谐波误差，可将表2中所求得各次谐波误差进行叠加，来求得零件的综合谐波误差。设零件的各次谐波误差之间存在线性关系，在高次谐波误差忽略不计的前提下，将各次谐波误差进行线性叠加，波形图如图6所示，其最大值为29.743 62 μm.

由表3可知，在高次谐波误差忽略不计的前提下，前5次谐波误差叠加后的综合谐波误差与圆柱度误差几乎一致，其差值为测量误差和高次谐波误差共同作用的结果。

图6　各次谐波误差叠加后波形图Fig.6　Waveform of overlaid harmonic errors

误差类型综合谐波误差圆柱度误差误差值/μm29.7436230.19145

为实现对零件加工后表面实际形貌的预测，可应用空间点矢量法确定测量点的实际位置及与理论位置的偏离程度，根据所有测量点实际位置拟合零件表面的预测形貌。将零件形貌预测结果反馈给上游的设计、工艺人员，以便设计、工艺人员根据谐波误差分析结果及表面预测形貌对零件质量进行综合评价，对设计结构进行优化并改进工艺过程。

被测元素实测数据如表4所示，将表4中数据代入(8)式，可得对角矩阵S，即被测元素表面矢量变换情况。

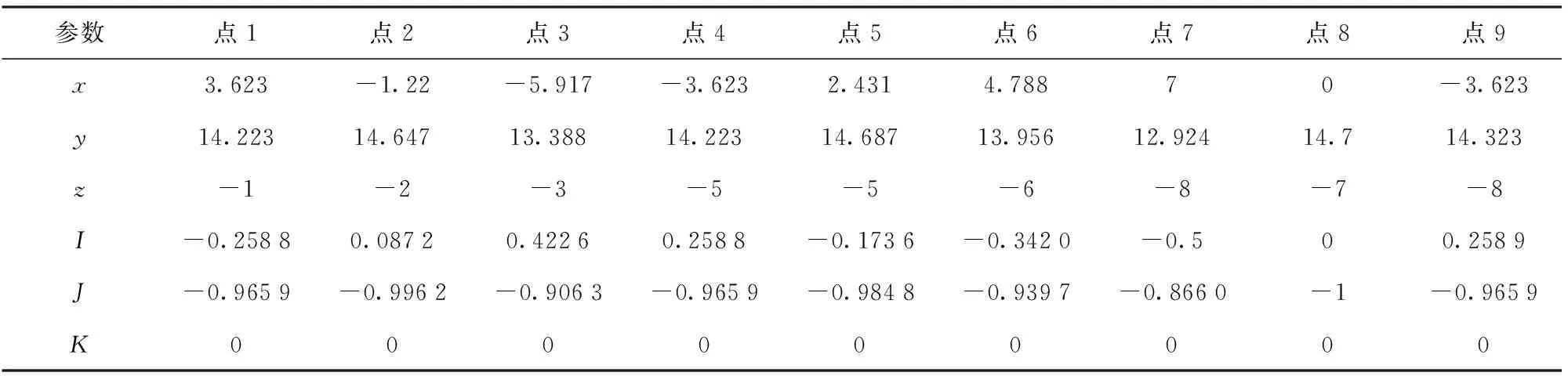
表4　被测元素实测数据

结合被测表面曲矢量化情况和拟合曲面即可得到被测元素表面的实际形貌，如图7所示。由(8)式可得S=

图7　被测元素表面实际形貌Fig.7　Actual surface morphology of detected elements

5　结论

1) 针对轴孔零件检测中的误差分析与表面形貌预测的问题，根据谐波理论和坐标测量原理，提出了轴孔零件形状误差的谐波分离方法和表面实际形貌预测方法。

2) 利用傅里叶变换将各次谐波误差分离出来，用各次谐波误差代替被测零件的圆柱度误差，并根据各次谐波误差的产生机理和其物理意义，提出了控制谐波误差的具体措施。应用线性叠加的方法将对零件影响比较大的各次谐波进行叠加，得到综合谐波误差。

3) 根据空间点矢量法来获得测量点的实际位置，通过测得的数据拟合被测特征并根据测量点的偏离程度对零件表面形貌进行预测。可合理、准确地预测出被测零件表面的实际形貌，便于上游环节根据谐波分析结果和被测零件表面实际形貌来优化设计零件结构、改善工艺过程。

4) 通过实际测量验证了谐波分析法在零件轴、孔类特征质量评价中应用的准确性，为轴、孔类零件特征的质量评价与分析提供了一种新的思路。

References)

[1]蒲静秋，罗正国. 谐波分析技术在回转体测量中的应用[J].仪器仪表学报，2004,25(4):117-119.

PU Jing-qiu, LUO Zheng-guo.Application for harmonic analysis in measure of rewind[J]. Chinese Journal of Scientific Instrument, 2004,25(4):117-119.(in Chinese)

[2]Capello E, Semeraro Q. The harmonic fitting method for assessment of the substitute geometry estimate error. PartⅡ:statistical approach, machining process analysis and inspection plan optimisation[J].International Journal of Machine Tools and Manufacture,2001,41(8):1103-1129.

[3]雷贤卿，李言，李济顺，等. 3点法圆度误差分离技术新算法[J].兵工学报，2007,28(1):73-77.

LEI Xian-qing, LI Yan, Li Ji-shun, et al. A new matrix algorithm of three-point method roundness error separation technique [J]. Acta Armamentarii, 2007,28(1):73-77. (in Chinese)

[4]谷伟,谭久彬.一种基于单转位特征角的圆度误差分离方法研究[J].光电子激光,2015,26(12):2358-2362.

GU Wei, TAN Jiu-bin. Research on the roundness error separation method based on single transposition characteristic angle[J]. Journal of Optoelectronics·Laser, 2015,26(12):2358-2362. (in Chinese)

[5]林玉池，刘治军，吴敬国. 轴类零件参数综合检测[J].中国机械工程，2000,11(3):295-298.

LIN Yu-chi，LIU Zhi-jun，WU Jing-guo. Integrative multi-parameter detection on complicated shaft[J].China Mechanical Engineering, 2000,11(3):295-298. (in Chinese)

[6]Li C, Yang D S. Applying particle swarm optimization algorithm to roundness error evaluation based on minimum zone circle[J]. Measurement, 2014, 52(6):12-21.

[7]崔长彩，黄富贵，张认成，等.粒子群优化算法及其在圆柱度误差评定中的应用[J].光学精密工程，2006,14(2):256-260.

CUI Chang-cai, HUANG Fu-gui, ZHANG Ren-cheng,et al.Research on cylindricity evaluation based on the particle swarm optimization(PSO) [J]. Optics and Precision Engineering,2006,14(2):256-260. (in Chinese)

[8]孙健. 基于线阵CCD回转体尺寸测量技术研究[D].长春：长春理工大学，2009.

SUN Jian. Research on measuring technique for revolving body sizes based on linear array CCD[D].Changchun:Changchun University of Science and Technology,2009. (in Chinese)

[9]Hsin Y L, Wen Y J, Chao K C. Precision modeling of form error for cylindricity evaluation using genetic algorithms[J].Precision Engineering,2000,24(4):310-319.

[10]Horikawa O, Maruyama N, Shimada M. A low cost, high accuracy roundness measuring system[J]. Precision Engineering, 2001,25(3):200-205.

[11]Cao L X. The measuring accuracy of the multistep method in the error separation technique[J].Journal of Physics E:Scientific Instruments,1989,22(11):903-906.

[12]Jariya B, Thammarat S, Salah H R, et al. Effect of step number on roundness determination using multi-step method[J].International Journal of Precision Engineering and Manufacturing,2013,14(11):2047-2050.

[13]李荣彬，张志辉，李建广. 超精密加工的三维表面形貌预测[J].中国机械工程，2000,11(8):845-849.

LI Rong-bin, ZHANG Zhi-hui, LI Jian-guang.Prediction of 3D surface topography in ultra- precision machining [J]. China Mechanical Engineering, 2000,11(8):845-849.(in Chinese)

[14]Lavernhe S, Quinsat Y, Lartigue C. Model for the prediction of 3D surface topography in 5-axis milling[J]. International Journal of Advanced Manufacturing Technology, 2010, 51(9):915-924.

[15]王先奎.机械制造工艺学[M].北京:机械工业出版社,2007.

WANG Xian-kui.Technology of mechanical manufacture[M].Beijing: China Machine Press, 2007.(in Chinese)

[16]罗永新. 高精度长轴类零件的加工误差分析与数控车削加工编程的编程对策[J].机械设计与制造，2004(6):102-103.

LUO Yong-xin. Parts manufacturing error analysis and the strategy of numerical control turning processing programming of high precision long axis[J].Machinery Design and Manufacture, 2004(6):102-103. (in Chinese)

[17]付丽华，边家文，李志明，等. 谐波信号分析与处理[M].武汉:中国地质大学出版社有限责任公司，2013.

FU Li-hua, BIAN Jia-wen, LI Zhi-ming, et al.Analysis and processing of harmonic signal[M].Wuhan:China University of Geosciences Press Co Ltd, 2013.(in Chinese)

[18]夏新涛，张青雷，李如强.轴承套圈加工表面谐波分布特征研究[J].磨床与磨削,1997(4):30-32

XIA Xin-tao, ZHANG Qing-lei, LI Ru-qiang.Research on harmonic distribution characteristics of bearing rings machined surface [J].Grinder and Grinding, 1997(4):30-32. (in Chinese)

[19]周祥才，朱兆武.检测技术及应用[M].北京:中国计量出版社,2008.

ZHOU Xiang-cai, ZHU Zhao-wu.Detection technology and application[M].Beijing: Chinese Metrology Press,2008.(in Chinese)

Error Separation and Surface Topography Prediction of Shaft and Hole Based on Harmonic Theory

SU Chang-qing， SUN Ye-xiang， QU Li-gang， YE Bai-chao， YANG Ye-guang

(Key Laboratory of Fundamental Science for National Defence of Aeronautical Digital Manufacturing Process， Shenyang Aerospace University， Shenyang 110136， Liaoning, China)

As one of the most widely used core parts in mechanical products, the shaft and hole parts tend to develop towards high precision, high strength and diversity. The quality control and quality evaluation are very important for shaft and hole parts. For the shape error separation of the shaft and hole parts, a harmonic separation method is proposed based on the research on the traditional error separation technique and the harmonic theory. According to the periodic data measured on the parts, the generation mechanism of each harmonic error is analyzed, and the measures to reduce the error are put forward. The actual position of the measuring point is obtained by using the space point vector method, and the surface topographies of the parts are predicted by combining with the surface fitting algorithm. The accuracy and rationality of the harmonic separation and surface topography prediction method are verified by experiments. Those methods provide a new idea for the surface quality evaluation and prediction of shaft and hole parts.

manufaturing technology and equipment; error analysis; harmonics measurement; topography prediction; harmonic theory; error separation

2016-02-19

国家自然科学基金项目(51005228、U1433109)； 沈阳航空航天大学航空制造工艺数字化国防重点学科实验室与中国空空导弹研究院合作项目(201601260216)

苏长青(1979—)，男，副教授，硕士生导师。E-mail:sucq@sau.edu.cn

TH161+.14

A

1000-1093(2016)10-1956-08

10.3969/j.issn.1000-1093.2016.10.024