面向对地打击武器-目标分配问题的遗传算法变量取值控制技术
王然辉, 王超
(1.61683部队, 北京 100094;2.火箭军工程大学, 陕西 西安 710025)
面向对地打击武器-目标分配问题的遗传算法变量取值控制技术
王然辉1, 王超2
(1.61683部队, 北京 100094;2.火箭军工程大学, 陕西 西安 710025)
对地打击目标与武器类型复杂多样,其武器- 目标分配问题难度较大,研究不足,而合理的武器- 目标分配方案,可优化资源配置,用最小的代价获取最大的战场收益。为此,构建相应数学模型,并针对采用遗传算法进行解算时收敛速度慢,甚至无法得出可行解等问题,设计了一种变量取值控制方法。该方法通过约束和控制初始种群个体中变量的取值范围来缩小搜索空间,提高搜索效率;通过改进变异策略扩大变量取值范围,确保解的质量。仿真结果表明,改进的遗传算法能有效地解决大规模对地打击武器- 目标分配问题,且性能较优。
兵器科学与技术; 武器- 目标分配; 毁伤贡献度; 遗传算法; 变量取值范围
0 引言
武器- 目标分配(WTA)是指挥决策中的关键问题,根据WTA中的目标是否具有威胁性,可分为广义的WTA与狭义的WTA[1]。防空武器- 目标分配(AD-WTA)属于典型的狭义WTA,国内外相关文献和研究成果很多,不同的算法都有各自的优势。对地打击武器- 目标分配(AG-WTA)属于广义WTA,由于其时效性要求没有AD-WTA高,问题比较复杂,相关的研究非常少见。
对地打击武器- 目标分配是现代战争中的重要问题。从美军近几场局部战争中可发现,赢得战争的重要手段是大量打击和毁伤对方地面目标,以达削弱其作战力量和瘫痪相关设施的目的,进而快速赢得战争。为达成作战目的,要选用大量的各型武器弹药打击各类地面目标。武器和目标的类型及数量众多,若不能合理分配打击资源,不仅需要投入过多的武器打击目标,造成大量的武器资源浪费,还可能延误战机,导致作战目的无法实现。因此,深入研究AG-WTA问题,建立合理的模型,设计高效的算法,是一项十分必要且非常紧迫的任务。
算法研究方面,王小艺等[2]、杨飞等[3]和张蛟等[4]提出了一种针对多约束WTA问题的粒子编码方案及模型的适应度函数,解决了粒子的整数域初始化问题,提高了粒子群优化算法的迭代效率及寻优能力。王玮等[5]针对遗传算法设计了一种满足约束条件的染色体编码格式,把求解问题转化为无约束的组合优化表现形式,为求解问题提供了新的思路。余家祥等[6]结合遗传算法、模拟退火算法和贪婪算法的优点,综合运用3种算法求解舰载武器目标分配问题。杨山亮等[7]在遗传算法的基础上,通过对初始种群编码机制的优化和采用精英选择及动态遗传算子的改进算法,较好地解决了WTA问题。
AG-WTA与AD-WTA有较大的差别。AD-WTA问题中,用于拦截空中目标的武器类型与数量较少,目标类型与数量也不多;用于拦截单个空中来袭目标的武器数量通常为1~2发;武器对目标毁伤属于0~1毁伤,无需考虑每发弹药对目标的累积毁伤效应;其优化原则是武器资源损失最小或敌方剩余目标数最少[8]。而AG-WTA问题中,打击地面目标的类型与数量很大,使用的武器类型多样、数量巨大;由于地面目标的复杂性,用于打击单个地面目标的武器用量也很大;不同武器,甚至不同类型的武器作用于目标时,要考虑累积毁伤效应;其优化原则是以最少的武器消耗达到预期目标毁伤要求。因此,AG-WTA问题的计算规模与解空间都远大于AD-WTA,现有WTA解决方案难以满足求解AG-WTA问题需要;且现有的方法存在因求解问题的维数过大而可能导致算法无法搜索到符合约束条件的解或搜索时间过长的问题[9],在实际作战筹划决策中是不允许出现的,因而需设计新的AG-WTA问题解决方案。
针对求解AG-WTA问题,本文首先构建AG-WTA模型,提出一种基于遗传算法的变量取值控制方法;而后定义贡献度概念,并以贡献度约束各型武器打击每个目标的用量和武器打击单目标的总用量,缩小变量初始化空间并使变量取值合理化,加快搜索到可行解;之后扩大变量变异范围,改变变异策略,消除因缩小变量取值范围可能造成的解空间缺失的问题,并加快算法收敛速度;最后进行算例仿真及对比,验证提出方法思路的正确性和优越性。
1 AG-WTA问题
1.1AG-WTA过程
AG-WTA主要包括两个阶段。
第一阶段:弹目匹配,即针对某具体目标,分析武器的战斗部毁伤机理、制导方式是否适用,预设阵地发射或防区外投射时射程能否覆盖目标,目标周围的环境是否满足武器的作战要求等,从而选出适宜打击该目标的武器类型。
第二阶段:分配优化,即综合考虑各型武器总量约束,将适宜的武器按照效费比最优的方式合理分配给目标,使所有目标达到预期毁伤效果。
1.2AG-WTA问题模型
弹目匹配阶段涉及的因素非常多,分析过程非常复杂,但结果只有“适宜”或“不适宜”两种,无需也无法进行优化。
因此,AG-WTA问题模型主要针对分配优化阶段进行设计。首先假设:
1)适宜的武器对目标的毁伤概率为考虑了突防、命中和毁伤等因素的综合毁伤概率,且同种类型武器对同类目标的综合毁伤概率相同;
2)不适宜的武器对目标的毁伤概率为0;
3)为降低风险,所有武器平台均在防区外进行发射,武器的价值消耗不包含武器平台受损部分;
4)暂不考虑目标打击的先后顺序,以及一个波次的最大投射能力限制。
基于上述假设,简要描述AG-WTA问题:有N型武器打击M类地面目标,使得M类目标的毁伤分别达到C1,C2,…,CM. 其中,N型武器数量分别为N1,N2,…,NN,其价值分别为V1,V2,…,VN;M类目标数量分别为M1,M2,…,MM,第i型武器打击第j类目标的综合毁伤概率为pij(i=1, 2,…,N;j=1, 2,…,M)。武器- 目标最佳分配目标是以最小武器价值消耗满足目标毁伤要求,设第i型武器作用于第j类第k个目标的数量为mijk(k=1, 2,…,Mj),武器消耗价值为V,则AG-WTA问题模型为
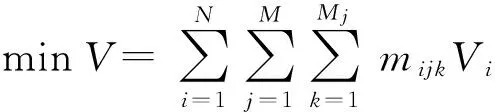
(1)
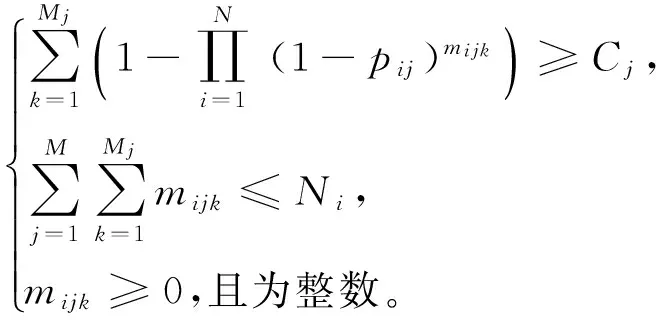
(2)
2 遗传算法的变量取值控制技术
遗传算法的基本思想来源于生物的遗传进化,模拟自然界生物群体优胜劣汰的进化过程,能够有效地处理多种优化问题[10],经过算法改进[5-8,11,12]已在WTA问题中得到了广泛应用[1,9]。生物群体的遗传进化起始于初始种群,初始种群的优劣直接影响个体进化的速度与方向,若遗传算法中的初始种群相对接近于最优个体,则将很快进化为最优个体。因此,可以针对遗传算法设计一种变量取值控制技术,通过控制变量取值范围使得初始种群个体在可行解空间内产生,从而有效提高解的质量和计算效率。
2.1控制变量取值的意义
AG-WTA问题是NP完全问题,算法搜索空间随着变量数量的增加或变量取值范围的扩大呈指数增加。在AG-WTA问题中,变量的个数是确定的、不可改变的,其值为武器类型数与目标数的积;但变量取值范围是不确定的,因AG-WTA一般不会约束各型武器作用于每个目标的用量,只会限制各型武器的可用数量,则在求解中作为变量取值范围的武器用量区间是不确定的、可改变的。若变量取值范围不作控制,即以每类武器的数量作为变量取值范围上界,则搜索空间内生成的WTA方案的数量极大。
假设有N型武器,其数量分别为N1,N2,…,NN;M类目标,其数量分别为M1,M2,…,MM. 若以各型武器的数量作为变量取值范围上界,则第i型武器打击第j类目标的武器用量mij的取值范围为
mij∈[0,Ni],mij为整数。
(3)
由(3)式可知,第i型武器打击第j类目标时,变量mij有Ni+1个可能取值。
对于第j类目标,N型武器打击该类第k个目标时,有N个变量,将其看作一个向量,则在这N个变量取值范围构成的搜索空间内,可生成的向量数量njk为
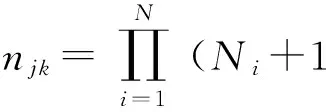
(4)
当N型武器打击第j类的所有目标时,有N×Mj个变量,则变量取值范围构成的搜索空间可生成的向量数量nj为
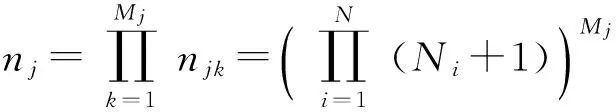
(5)

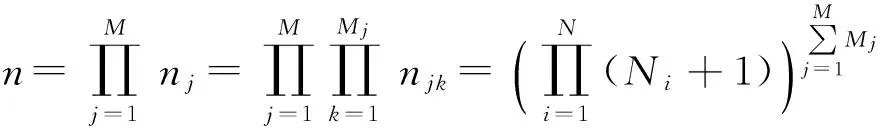
(6)
式中:向量数量n值,即为当N型武器打击M类全部目标时,所有可能的WTA方案数量。
从(6)式可以看出,随着变量取值范围增大,AG-WTA方案数量n值迅速增大。但AG-WTA问题的可行解数量为定值,只占全部分配方案数量的很少一部分,且绝大部分的可行解集中分布在搜索空间的某一区域,其分布区域和数量不受变量取值范围的影响。因此,若能急剧缩小搜索空间,并使搜索空间包含可行解所在的空间,就可确保快速搜索到可行解。
例如,有49发同种类型武器打击10个同类目标,若以武器总量作为变量取值上界,则N1=49,M1=10,根据(6)式可解算分配方案数量n(1)为
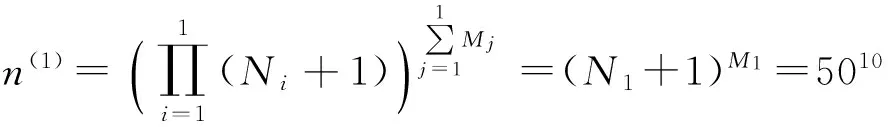
(7)
若控制变量取值范围,令其变量上界取值为9,则N1=9,M1=10,根据(6)式可解算分配方案数量n(2)为
n(2)=(N1+1)M1=1010.
(8)
由(7)式和(8)式解算的分配方案数量n(1)和n(2),可得无变量取值范围控制与有变量取值范围控制搜索空间内的分配方案数量之比α为
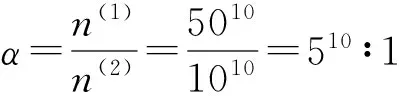
(9)
可见,在减小变量取值范围上界后,搜索空间急剧缩小,搜索空间内的分配方案数量也急剧减少,且缩小后的变量取值范围总体是合理的,其变量取值范围构成的搜索空间能够包含绝大部分可行解空间,表明变量取值范围的合理控制能确保快速搜索到可行解。
2.2基于毁伤贡献度确定取值范围
变量取值控制方法是通过对变量取值范围进行一系列操作来提高搜索效率,即在遗传算法初始化过程中缩小算法搜索空间,以缩短解算时间;在变异过程中放大变量取值范围,确保有合理的解算结果。对于遗传算法求解AG-WTA问题,变量为各型武器作用于每个目标的数量,变量取值范围是各型武器可能作用于每个目标的数量区间。变量取值控制由三部分构成:一是约束各型武器作用于每个目标的最大数量;二是约束作用于每个目标的武器总量;三是扩大变量变异区间并改变变异策略。
对于同一个目标,要达到预期的毁伤效果通常会使用n枚武器进行打击,对于同一种武器而言,每枚武器会贡献不同的毁伤值,可称之为毁伤贡献度,用u表示。若第i型武器打击第j类目标的毁伤概率为pij,则第n发的毁伤贡献度为
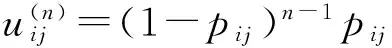
(10)
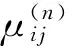
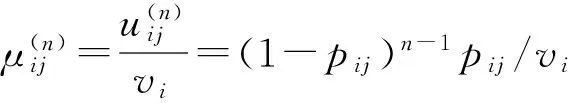
(11)
显而易见,对于同一目标,在选择武器时,单位价值毁伤贡献度越大的武器越适宜。
2.2.1约束各型武器作用于每个目标的数量
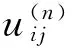
(12)
因此,第i型武器打击第j类目标的武器用量区间上界值tij为
tij=n-1.
(13)
2.2.2约束作用于每个目标的武器总数量
武器类型不同、毁伤概率各异,但存在多型武器都适用于打击同一目标的情况,对于这种情况,在遗传算法的种群初始化中,就会给各型适用武器都随机赋予打击该目标的武器用量数值,且数值为0的可能性小,从而可能会出现作用于该目标的武器数量过多,导致在后续的优化中要消耗大量的时间将作用于该目标的武器数量降到合理的范围。显然,打击某个j类目标的武器总量,不应大于对j类目标毁伤概率最小(min(pij),i=1, 2,…,N)的武器的取值上界。设有N型武器适用于打击第j类目标,则作用于该类每个目标的武器总数量最大值Tj为
Tj=max (tij),i=1,2,…,N.
(14)
作用于目标的武器总数量最大值确定后,在算法程序中需对N型武器作用于该目标的数量m1j,m2j, …,mNj进行处理,使得满足:
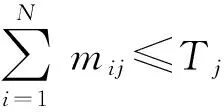
(15)
2.3通过定向变异放大变量取值范围
通过对各型武器作用于每个目标的数量和作用于每个目标的武器总数量进行约束,种群中个体变量可取值范围变小,这种变量取值范围约束总体是合理的。但当某型武器对某类目标的毁伤概率较小时,约束后作用于该类单个目标的该型武器数量可能不足以使其达到要求的毁伤程度,导致约束的变量取值范围内无可行解。假设第i型武器打击第j类目标,根据(12)式和(13)式可得第i型武器对每个第j类目标的武器最大用量tij,则其对第j类目标的最大毁伤程度βij为
βij=1-(1-pij)tij.
(16)
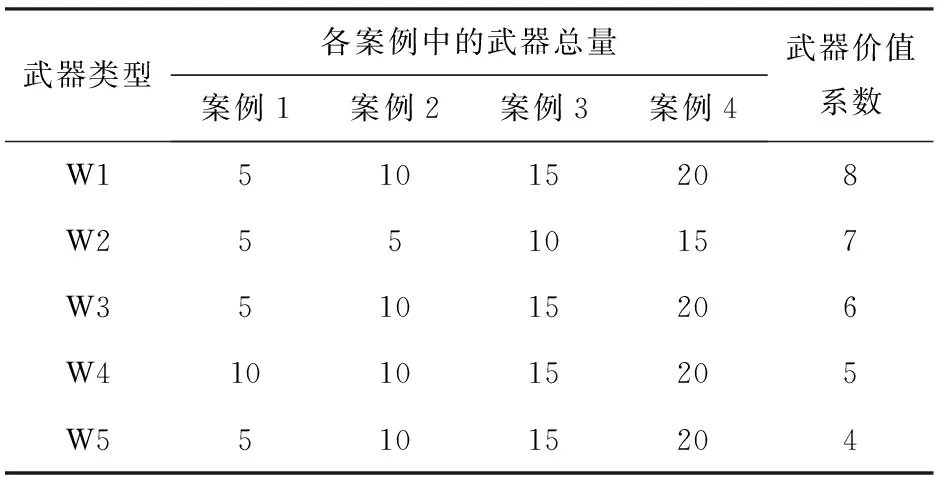
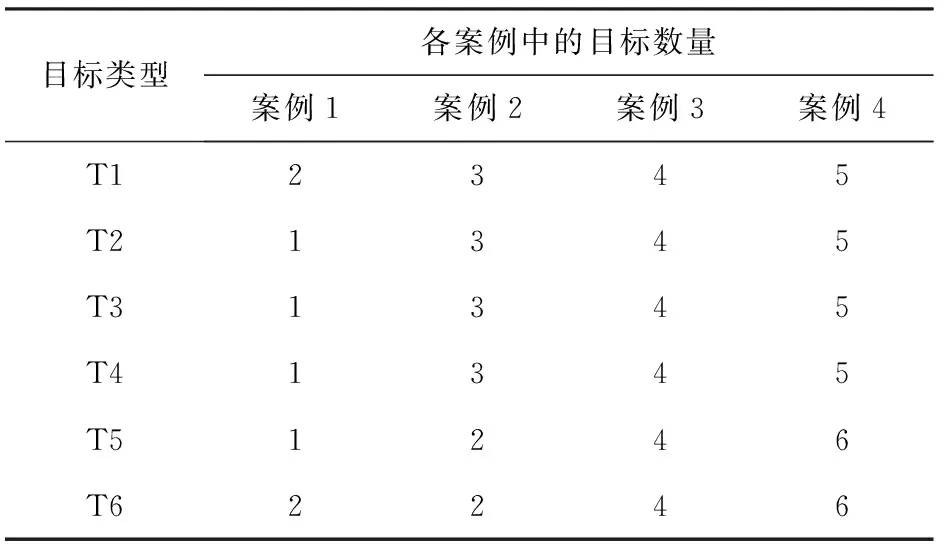
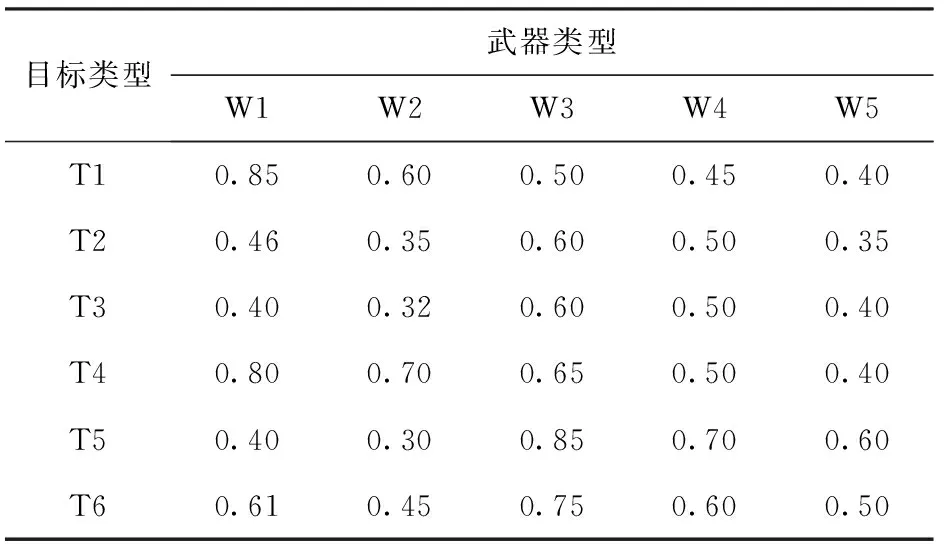
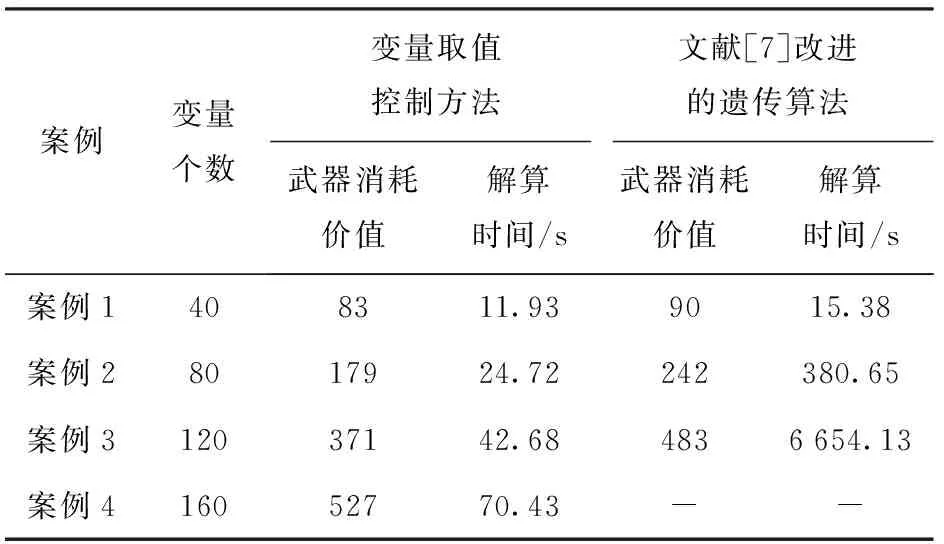
由(10)式和(12)式可得:当0 (1-pij)tijpij<αj≤(1-pij)tij-1pij, (17) 即 (18) 联立(16)式和(18)式又可得 (19) 因此, (20) 在变异操作过程中扩大变量范围,使变异过程中变量可取各型武器实有数量内的任意数值,确保搜索到可行解。变量取值范围的扩大增加了搜索空间,使得搜索可行解的时间变长,为避免该情况,采取动态定向变异。设某类目标要求的毁伤程度为alf0,种群个体中该类目标的实际毁伤程度为alf,若属于该类目标的一个变量值为pop(i,j),变量对应的某型武器实有数量为bound,则在变异过程中对其的操作流程如图1所示。 图1 遗传算法变异操作流程图Fig.1 Flow chart of mutation operation of genetic algorithm 2.4基于变量取值控制技术的遗传算法流程 变量取值范围控制方法应用于遗传算法求解AG-WTA问题的流程: 1) 约束各型武器作用于每个目标的数量。以武器的贡献度约束各型武器作用于每个目标的数量,控制初始种群变量取值范围。 2) 产生初始种群。在设定的变量取值范围内初始化种群。 3) 约束武器作用于每个目标的总数量。以作用于某个目标用量最大的单型武器使用数量max(tij),作为所有武器作用于该目标的最大用量,约束武器总数量Tj. 4) 控制初始种群变量值。计算种群个体中N型武器打击同一目标的用量总和T1j. 若Tj 5) 计算种群个体适应值,并进行复制和交叉操作。 6) 进行定向变异操,流程如图1所示。 7) 迭代终止。判断是否满足迭代次数要求,判断是否满足目标毁伤要求,若两个要求都满足,迭代终止;否则,转入步骤5. 2.5可行性分析 变量控制技术包括两个环节:在初始化阶段适当约束变量取值范围,压缩搜索空间,提高搜索效率;在变异迭代过程中,根据需要定向微调武器用量,确保解的质量,避免早熟。 由于对地打击某一目标可以是多型武器的优化组合,使得综合毁伤值达到预期毁伤要求,因此在种群初始化过程中,根据预期毁伤要求和每型武器的毁伤贡献度,适当约束作用于某个目标的单型武器数量和所有武器总量,可有效地缩小搜索空间,提高索搜效率。 变异过程中,根据现有武器对目标的综合毁伤值与预期毁伤要求之差来随机确定增加或减少武器用量。此时,武器用量不再受毁伤贡献度约束。若大于0,表示武器用量偏大,则随机减少某型武器数量;若小于0,表示武器用量偏小,则随机增加某型武器用量。从而确保每个目标均达到预期毁伤要求,即解可行;且尽量降低总的武器消耗价值,即解更优。 由于采用实数编码的方式,在变异过程中,无论是随机增加还是减少某型武器的用量时,都只对其中的一型武器加1或减1,而不是随意变换武器用量取值,通过反复实验,适当控制变异概率,较好地避免早熟的问题。 3.1AG-WTA问题实例 针对典型的AG-WTA问题,基于同一背景设置4个不同案例,进行对比分析。 案例背景:总共投入5种不同类型武器,各型武器的价值系数,以及每个案例中的总投入量如表1所示;打击一定数量的6类地面目标,每个案例中的目标数量如表2所示;已知各型武器对每类目标的毁伤概率如表3所示;要求每个目标的预期毁伤值达到0.9以上,求解最佳的武器分配方案。 表1 各类武器的价值及总量 表2 目标类型及其数量 表3 武器对目标的毁伤概率 3.2AG-WTA问题仿真与分析 针对以上案例,运用Matlab软件,在相同的软硬件(Win7 x64,Intel(R) Xeon(R) CPU E3-1240 v3 @3.4 GHz,RAM 16 GB)条件下,分别对文献[7]的改进遗传算法和本文提出的解算方法求解AG-WTA问题编程仿真,记录两种算法优化的武器消耗价值及解算消耗的时间,其结果如表4所示。 表4 两种改进算法的解算结果及消耗时间对比 注:表中“变量个数”为“武器类型数量×目标个数”,“-”表示未解算出相应结果。 从表4可以看出,本文采用基于毁伤贡献度的变量取值控制技术对遗传算法进行改进,相比文献[7]改进的遗传算法,计算结果更优、效率更高,而且随着变量个数(即武器种类和目标数量)的增加,其效果更明显。 针对AG-WTA这一类特殊问题,本文采取变量控制的方法对遗传算法进行改进,有两个方面的优势:一是合理压缩搜索空间,大大地提高计算效率;二是改进变异策略,确保了解的质量,有效避免早熟等现象。通过反复实验和对比分析,该方法针对大规模AG-WTA问题,在解的质量和计算效率方面具有明显优势,且规模越大时优势越明显。 需要指出的是,本方法在求解AG-WTA问题时具有明显优势,不适应于求解AD-WTA问题,针对于其他复杂优化问题是否有效还有待进一步研究。 References) [1]蔡怀平, 陈英武. 武器- 目标分配(WTA)问题研究进展[J]. 火力与指挥控制,2006,31(12):11-15. CAI Huai-ping,CHEN Ying-wu. The development of the research on weapon-target assignment (WTA) problem [J]. Fire Control and Command Control, 2006, 31(12):11-15. (in Chinese) [2]王小艺, 刘载文, 侯朝桢, 等. 防空武器多目标优化分配建模与决策[J]. 兵工学报,2007,28(2):228-231. WANG Xiao-yi, LIU Zai-wen, HOU Chao-zhen, et al. Modeling and decision-making of multi-target optimization assignment for aerial defense weapon[J]. Acta Armamentarii, 2007, 28(2):228-231. (in Chinese) [3]杨飞, 王青, 侯砚泽. 基于整数域改进粒子群优化算法的多平台武器目标分配[J]. 兵工学报, 2011, 32(7):906-912. YANG Fei, WANG Qing, HOU Yan-ze. Weapon-target assignment in multi-launcher system based on improved integer field particle swarm optimization algorithm[J]. Acta Armamentarii, 2011, 32(7):906-912. (in Chinese) [4]张蛟, 王中许, 陈黎, 等. 具有多次拦截时机的防空火力分配建模及其优化方法研究[J]. 兵工学报, 2014, 35(10):1644-1650. ZHANG Jiao, WANG Zhong-xu, CHEN Li, et al. Modeling and optimization on antiaircraft weapon-target assignment at multiple interception opportunity[J]. Acta Armamentarii, 2014, 35(10):1644-1650. (in Chinese) [5]王玮, 程树昌, 张玉芝. 基于遗传算法的一类武器目标分配方法研究[J]. 系统工程与电子技术, 2008, 30(9):1708-1711. WANG Wei, CHENG Shu-chang, ZHANG Yu-zhi. Research on approach for a type of weapon target assignment problem solving by genetic algorithm[J]. Systems Engineering and Electronics, 2008, 30(9):1708-1711. (in Chinese) [6]余家祥, 王绍华, 程文鑫. 基于改进局部搜索遗传算法的目标分配决策[J]. 系统工程与电子技术, 2008,30(6):1114-1117. YU Jia-xiang, WANG Shao-hua, CHENG Wen-xin. Target allocation decision making based on improved genetic algorithms with local search[J]. Systems Engineering and Electronics, 2008, 30(6):1114-1117. (in Chinese) [7]杨山亮, 黄健, 刘洋, 等. 基于遗传算法的联合火力 WTA 问题研究[J]. 计算机仿真, 2012, 29(3):61-63. YANG Shan-liang, HUANG Jian, LIU Yang, et al. Analysis of weapon target assignment problem in joint fire strike solving by genetic algorithm[J]. Computer Simulation, 2012, 29(3):61-63. (in Chinese) [8]Lee Z J, Su S F, Lee C Y. Efficiently solving general weapon-target assignment problem by genetic algorithms with greedy eugenics[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2003, 33(1): 113-121. [9]李勇君, 黄卓, 郭波. 武器- 目标分配问题综述[J]. 兵工自动化, 2009, 28(11):1-5. LI Yong-jun, HUANG Zhuo, GUO Bo. Review of weapon-target assignment problem[J]. Ordnance Industry Automation, 2009, 28(11):1-5. (in Chinese) [10]Aytug H, Khouja M, Vergara F E. Use of genetic algorithms to solve production and operations management problems[J]. International Journal of Production Research, 2003, 41(17): 3955-4009. [11]李平,李长文. 武器目标协同火力分配建模及算法[J]. 指挥控制与仿真, 2015, 37(2):36-40. LI Ping, LI Chang-wen. Modeling and algorithm of weapon target cooperative fire assignment[J]. Command Control & Simulation, 2015, 37(2):36-40. (in Chinese) [12]武从猛, 王公宝. 遗传- 蚁群算法在目标分配问题中的应用研究[J]. 兵工自动化, 2014, 33(4):8-11. WU Cong-meng, WANG Gong-bao. Application of genetic ant-colony algorithm in target assignment problem[J]. Ordnance Industry Automation, 2014, 33(4):8-11. (in Chinese) Variable Value Control Technology of Genetic Algorithm for WTA of Ground Target Attacking WANG Ran-hui1, WANG Chao2 (1.Unit 61683 of PLA, Beijing 100094, China; 2.Rocket Force University of Engineering, Xi’an 710025, Shaanxi, China) Research on weapon-target assignment (WTA) of ground target attacking is very difficult due to a wide variety of targets and weapons. A reasonable WTA scheme is developed to optimize the allocation of limited resources, which brings the maximum battlefield gains with minimum costs. For this reason, a mathematical model is established, and the genetic algorithm is used to resolve the optimal result of weapon-target assignment. But the convergence rate of genetic algorithm is slow and can’t even give a feasible solution in solving WTA. A state variable control method is designed to overcome the insufficient of the genetic algorithm. The proposed method can reduce the search space and improve the search efficiency by restraining and controlling the value range of the initial population variables, and ensure the quality of the solution by improving the mutation strategy to expand the value range of the variables. The simulated result shows that the improved genetic algorithm can solve the WTA problem of attacking the ground targets on a large scale effectively. ordnance science and technology; weapon-target assignment; damage contribution; genetic algorithm; value range of variables 2015-06-09 王然辉(1980—),男,工程师。E-mail: w_ranhui@163.com O22.6 A 1000-1093(2016)10-1889-07 10.3969/j.issn.1000-1093.2016.10.016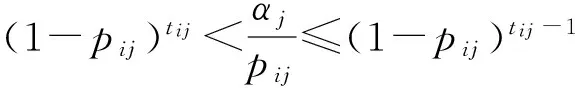
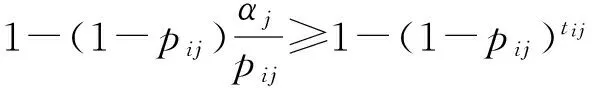
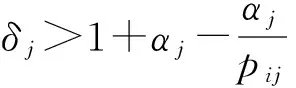

3 计算案例
4 结论

