基于Dempster-Shafer证据理论的通信辐射源个体识别算法

郭晓陶， 王星， 周冬青

(空军工程大学 航空航天工程学院, 陕西 西安 710038)



基于Dempster-Shafer证据理论的通信辐射源个体识别算法

郭晓陶， 王星， 周冬青

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

针对由于各种信号干扰和传感器误差导致辐射源个体正确识别率较低的问题，提出一种多传感器融合识别算法进行复杂电磁环境中的通信个体识别。该算法将Dempster-Shafer证据理论和特征提取结合起来，充分利用侦测的信号特征，减少了识别过程中的不确定信息。该融合识别算法提取侦测信号中的个体特征，使用基于决策向量的自适应证据融合方法将由个体特征转化而来的多个证据相融合，最后再根据判决准则得到最终的识别结果。分别对自适应融合方法和融合识别算法进行仿真分析，结果表明自适应证据融合方法可以综合考虑融合过程的计算效率和融合结果的合理性，在二者之间达到平衡。与现有的识别方法相比，多传感器融合识别算法可以提高复杂电磁环境中个体识别的稳定性和正确识别率。

兵器科学与技术； 辐射源识别； 信息融合； Dempster-Shafer证据理论； 特征提取； 自适应证据组合

0　引言

随着通信技术的不断发展，电台的种类和数目也呈现指数式增长的态势，在战场上实现对敌方通信电台的侦察和个体识别也成为信息化战争的基础和关键。目前对于通信辐射源的个体识别主要从通信信号的瞬态部分和稳态部分两个方向进行研究[1]，瞬态信号相较于稳态信号具有更为丰富的非线性特性和个体特征，因此利用瞬态信号往往具有更高的识别成功率。但是其出现时刻较为随机，持续时间较短，只有几毫秒到几十毫秒，因此对于瞬态信号的截获通常存在一定的难度，而且侦收到的瞬态信号可能并不完整，存在一定的不确定性。基于以上分析，如何更好地利用瞬态信号进行个体识别是目前需要解决的问题。

Dempster-Shafer证据理论在处理不确定性信息时有其独特的优势[2-3]，并且可以在决策层进行信息融合，大大减少了数据的运算量。但是Dempster-Shafer证据理论目前仍然存在两个关键问题阻碍其广泛应用：1) Dempster-Shafer证据理论中基本概率赋值(BPA)函数的获取缺乏坚实的理论支撑，现有的mass函数主要通过专家确认和已有经验判断，受主观因素影响较大，无法从理论上进行论证；2)Dempster组合规则在处理强冲突证据时存在不足，会产生与实际情况相悖的结论。对于前者，文献[4]提出基于区间数的BPA生成方法，文献[5]则提出基于不确定优化模糊函数的BPA生成方法。对于后者，文献[6]提出基于置信最大熵的推理方法，文献[7]提出冲突程度推定的组合规则。

为了解决瞬态信号截获难度大、信息存在缺失的问题，本文提出了基于Dempster-Shafer证据理论的多传感器融合识别算法。首先使用文献[8]的方法将提取的特征信息转化为mass函数，使得到的BPA值具有更严谨的理论依据和逻辑性。由于通信辐射源瞬态信号的特殊性，单个传感器接收到的数据通常存在缺失的问题，因此本文使用基于决策向量的自适应证据融合方法对多个传感器得到的证据信息进行融合再识别。这种融合识别方法既能有效地减少人为干扰和背景噪声对识别的恶化，又避免了由于单个传感器存在的误差造成的误识别。仿真结果表明，本文提出的融合识别算法具有较好的合理性和有效性。

1　自适应证据融合方法

经典Dempster-Shafer证据理论中的Dempster规则在处理低冲突证据时具有数学性质好、收敛速度快等优势；但是当冲突程度较大时，会出现稳定性差和“0”悖论等问题[9]。为了克服以上缺点，并充分利用Dempster规则的特点，本文提出利用基于决策向量的自适应组合方法进行信息融合。

已有的融合方法主要通过冲突因子K判断证据间的冲突程度，冲突因子可以反映不同证据对所支持目标的一致性和明确性程度。而文献[10]中提出的证据距离可以衡量各个证据间整体上的差异程度，证据间差异越小，则证据距离越小。因此，冲突因子和证据距离在描述证据的冲突程度时具有很好的互补性。证据距离定义为

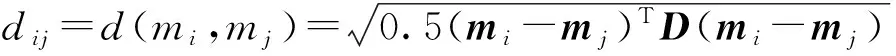
(1)

式中：mi和mj是同一识别框架中第i个目标和第j个目标的mass函数；mi和mj为由识别框架中2n个元素构成的2n维空间中的n维向量；D为2n×2n维正定系数矩阵, 若A、B为同维矩阵，则D(A,B)=|A∩B|/|A∪B|. 影响证据冲突程度的因素有很多，单独使用冲突因子K或者证据距离d不能全面、准确地表示证据间的冲突程度。因此本文结合两方面的特点提出决策向量Vd来全面衡量证据间的冲突程度，即Vd由冲突因子K和证据距离d联合表示，是二者构成的二维向量：Vd=[K,d]，这里d为证据距离的平均值。设α和β是根据决策向量设定的阈值，下面分别分析各种情况的算法原理：

1)当K<α且d<β时，可认为证据间的冲突程度低且一致性较好，可以直接使用Dempster规则进行信息融合。

2)当K≥α且d<β时说明存在冲突证据，可用参考证据对冲突证据进行替换。首先计算证据间的相似度，设mi和mj是同一识别框架中的mass函数，则mi和mj的相似度为

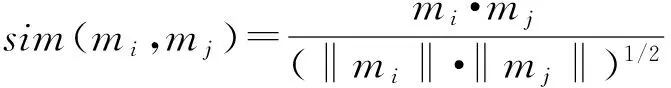
(2)

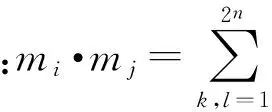
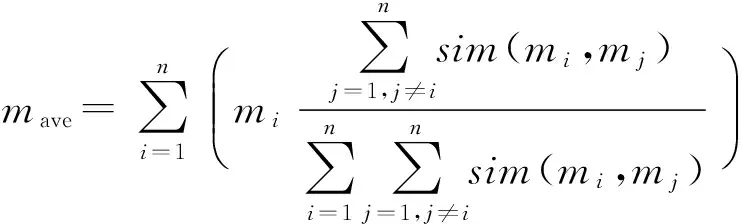
(3)

某一证据与其他证据的相似度越小，则其在参考证据中所占的比重也就越小。因此使用参考证据进行替换可以降低冲突证据对融合结果的影响。

3)当K<α且d≥β时说明存在证据因强干扰或电磁环境扰动等原因而与其他证据整体差异较大。这时需要对证据源的权重进行赋值，从而降低差异证据在融合过程中所占的比重。证据的可靠性系数定义为

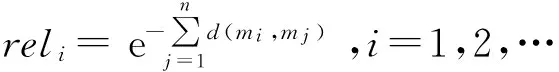
(4)

可靠性系数反映了某一证据与其余证据间的差异程度，其值越高，则在全部证据中该证据的一致性就越好。除此之外，不确定性系数定义为

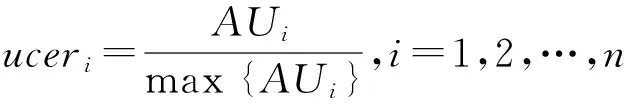
(5)

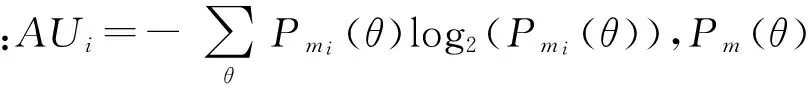
(6)

式中：|A|是集合A的基。Pignistic概率函数的实质是将一个BPA转化为概率分布，从其计算公式可知Pignistic概率函数是将多命题焦元对应的信度依据均分的思想分配到各单焦元命题上。这种转化方法与熵最大化类似，会造成已有信息的大量损失。因此，文献[11]中提出一种基于信任函数和似真函数的概率转化方法，其公式为

(1-ΣBel)+Bel(Ai),

(7)

式中：ΣBel为所有单子集焦元的概率累加；Bel和Pl表示识别框架的置信函数和似然函数。这种方法综合考虑了信任函数和似真函数在mass函数分配中的影响程度，充分利用了已知信息，更具合理性。可靠性系数反映了其他证据对该证据的支持程度，不确定性系数则反映了证据自身的清晰程度。二者分别从证据源的外部和内部度量证据的可靠程度，因此证据源的修正因子定义为

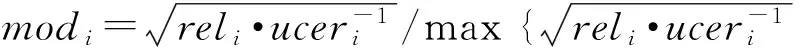
(8)

根据修正因子所包含的意义对证据源的权重进行赋值，规则为

(9)

4)当K≥α且d≥β时首先用参考证据将冲突证据替换，再判断得到的新证据间的距离是否大于β. 如果大于β，则用修正因子对证据源的权重赋值再进行数据融合，否则直接进行融合。其关系如图1所示。

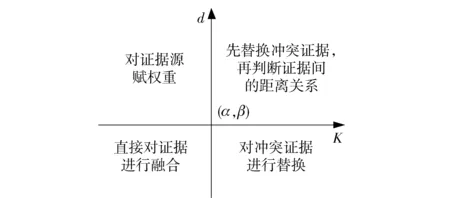
图1　自适应融合方法关系分布图Fig.1　Distribution of self-adaptive fusion rule

算法中的参数α和β一般根据实际情况进行选取。二者数值取得越大，算法的自适应选择风险也就越大，但取得过小则不利于算法的快速收敛，影响识别的实时性和快速决策。经过多次仿真实验，在保证融合效果的前提下减少算法的复杂度，得到针对本文数据类型的阈值为K=0.7，d=0.5.

2　多传感器融合识别算法

基于Dempster-Shafer证据理论对辐射源个体进行识别的原理框图如图2所示。图中u0,u1,…,uj为识别框架中所有元素，mi(u0),mi(u1),…,mi(uj)为第i个传感器获取的mass函数，mi(·)为分配到目标个体uj上的信度函数值。每个传感器把截获到的通信瞬态信号通过特征提取转换到证据空间，即对每一个对象进行BPA赋值，并对所得的证据进行信息融合，最后根据一定的判决准则确定通信辐射源的个体身份。其具体步骤如下：

1)获取基本概率函数。首先将通信信号中的非线性特征提取出来，再依据一定的准则将特征值转化为识别框架中的mass函数，转到步骤2.

2)冲突判断。计算所有证据间的冲突因子K. 如果K>α，说明证据间的冲突程度较高且存在冲突证据，因此需要替换冲突证据，转到步骤3；否则，转到步骤4.

4)一致性判断。根据(1)式得出mi和mj的证据距离，并计算所有证据距离的平均值d. 如果d>β，则证据整体上的一致性较差，需要对证据源进行修正，转到步骤5；否则，转到步骤6.

5)修正证据源。根据(8)式得到每个证据的修正因子，再根据(9)式对证据源进行修正，转到步骤6.

(10)

式中:ε1和ε2是提前确定的阈值。

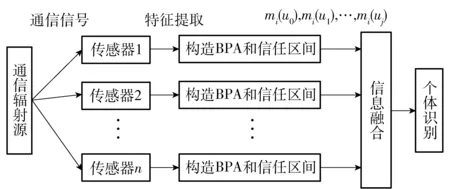
图2　　　　基于Dempster-Shafer证据理论的通信辐射源个体识别框图Fig.2　Functional block diagram of emitter identification

只有当所有准则同时满足时可判定A1为识别结果，如果不能全部满足说明现有数据不能支持目标识别。识别算法的流程图如图3所示。

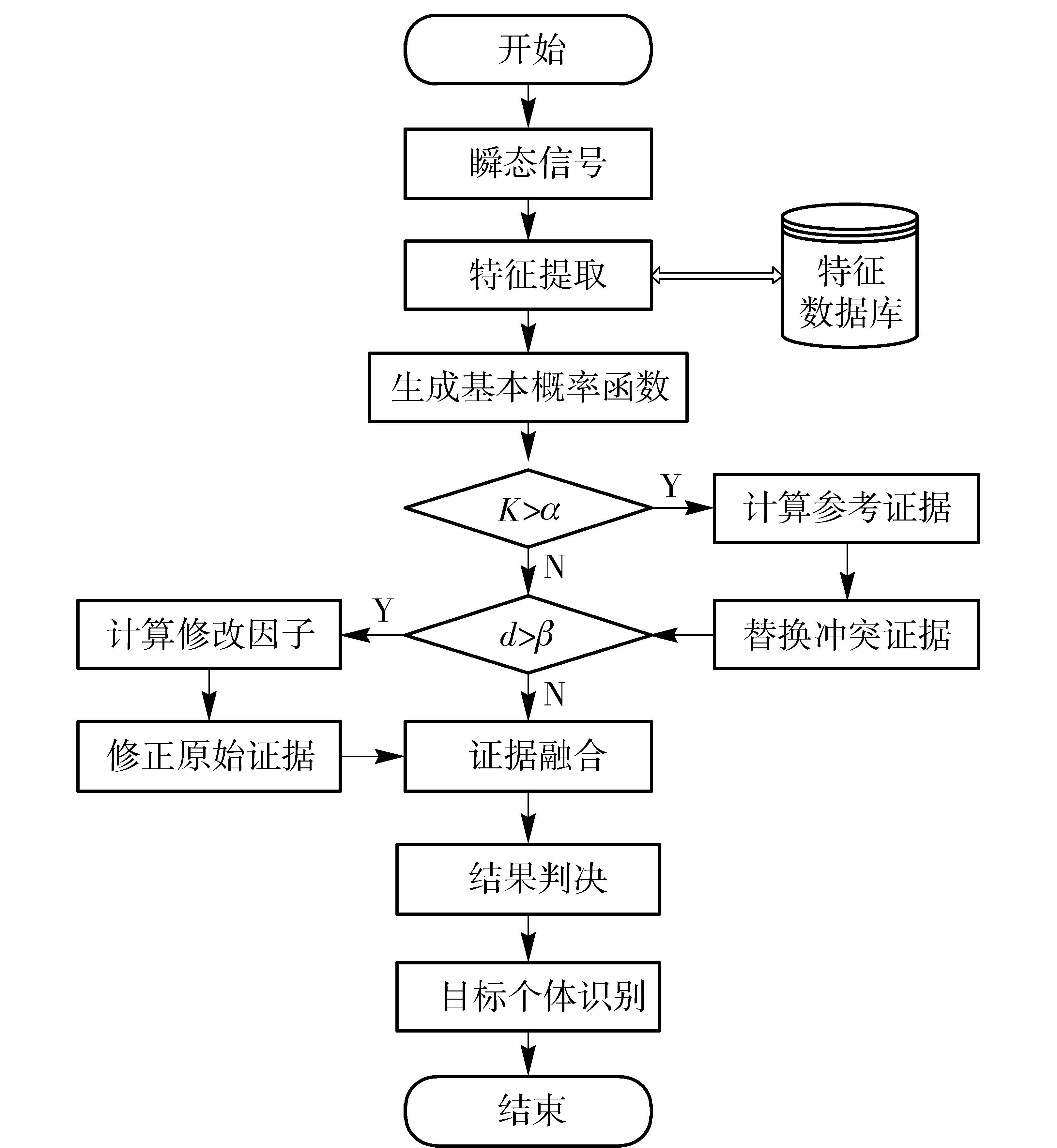
图3　多元信息融合识别算法的流程图Fig.3　Flow chart of sequential identification algorithm

3　仿真分析

为了验证本文提出的识别算法的可行性与有效性，仿真分为两部分进行：第1部分分别在低冲突证据与高冲突证据情况下对自适应证据融合算法的融合效果进行仿真，并与其他现有融合算法进行对比；第2部分在给定的仿真条件下对多源信息融合识别算法进行想定仿真，并与其他通信个体识别算法进行对比。

3.1自适应证据融合算法

此处仿真数据均来自于文献[13]。设目标识别框架为Ω={a,b,c}，a、b、c为框架中所有元素，即可能的目标个体。共有4条不同的证据。表1为低冲突时的证据值，表2为高冲突时的证据值。本文方法中取K=0.7，d=0.5.

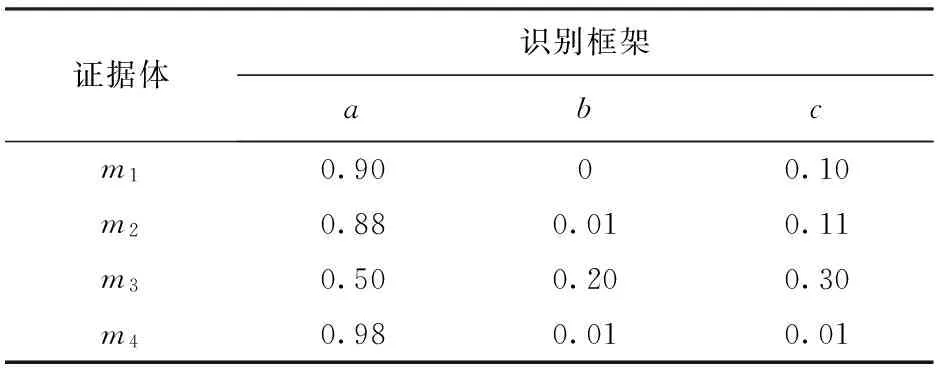
表1　低冲突的BPA值

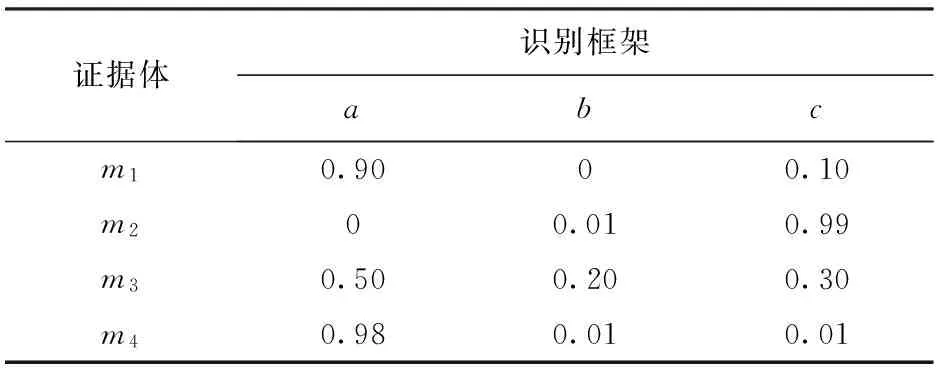
表2　高冲突的BPA值

低冲突数据的融合结果如表3所示。由表3可知，随着证据个数的增多，文献[14]的算法将冲突部分分配给了未知集，这不利于证据融合的收敛和融合结果的判断。Dempster和文献[15]的算法最终可以趋于收敛并正确判定最终结果为a，但Dempster组合方法在两个证据进行融合时就达到收敛，而文献[15]的算法到4个证据进行融合时才趋于收敛。因此在证据的冲突程度不高时，Dempster组合规则能够在融合效率和融合结果的正确性之间实现较好的平衡。此外，Dempster组合方法保证了证据理论具有交换律和结合律等良好数学性质，并且随着证据个数的增加实现对支持度的累加，而这些都是文献[15]和文献[16]的算法不具备的。因此，自适应证据融合算法在判决决策向量Vd小于设定的阈值时可以直接选择Dempster组合方法实现对证据的融合。这样既提高了算法的计算效率，满足融合的实时性，又保证了证据融合的合理性和正确性。

如表4所示，当证据之间的冲突程度较大时，直接使用Dempster组合规则就会出现“一票否决”和稳定性差等问题，并可能得出与实际情况相悖的结果。文献[14]和文献[16]的算法虽然避免了Dempster组合方法的问题，但是证据之间互相冲突的部分被分配给了未知集，这种解决方式与通过信息融合提高对正确识别对象支持度的主要思想相违背，不利于对融合结果的判定。与此同时，文献[15]的算法较前3种算法有所改进，可以根据不同证据源的重要程度进行加权融合，但是其收敛速度较为缓慢，在4个证据进行融合时仍不能对正确识别目标达到较高的支持度。与现有算法相比，本文提出的自适应融合算法首先判决决策向量Vd是否大于设定的阈值，当判决冲突程度较大时，可以通过用参考证据替换冲突证据从而降低证据之间的冲突程度。此外，自适应融合算法还以计算各个证据的修正因子，依据修正因子的大小决定不同证据源在信息融合过程中所占的权重，这样就提高了可靠证据对正确识别目标的支持度。从表4可知，自适应融合算法在应对高冲突证据时也可以较快地实现收敛，同时避免产生与实际情况相悖的结论。

表3　低冲突证据的融合结果

表4　高冲突证据的融合结果

3.2多源信息融合识别算法

为了实现通信辐射源的个体识别，用于识别的个体特征必须具有时移不变性、尺度变化性和相位保持性等特性，如信号的分形、小波系数和高阶累积量等特征。因此，本文选择区分效果较为理想的双谱、小波特性及谱特征作为区分不同辐射源的个体特征。

设电磁环境中共有3种可能存在的通信辐射源，即多传感器目标识别体系的设识别框架由3个待识别目标A、B、C组成：Ω= {A,B,C}。系统使用S1、S2和S3共3种侦测设备传感器，它们是独立的完全不同的知识源，能反映相同或不同的目标频谱和空间特性。仿真设定真实的目标对象为A且信号传输信道的信噪比为0 dB，辐射源信号的原始波形图如图4所示。对接收到的信号分别分析其双谱、小波特性及谱特征。图5为传感器S1侦收到的信号通过小波变换得到的特征信息。其中设定小波系数的分解层数n=7，CD1～CD7为细节系数，CA7为近似系数。图6为传感器S2侦收到的信号通过提取双谱特性得到的特征信息。图7为传感器S3侦收到的信号的光谱特性图。将得到的特征信息通过文献[8]转换为不同的mass函数值，如表5所示，其中，m1、m2和m3分别是通过S1、S2和S3传感器侦测到的信号特征信息转化成的mass函数值。本文方法中取K=0.7，d=0.5.

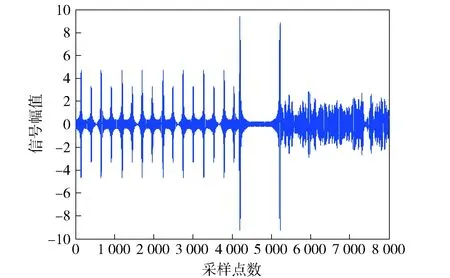
图4　辐射源信号波形图Fig.4　Original signal waveform of emitter

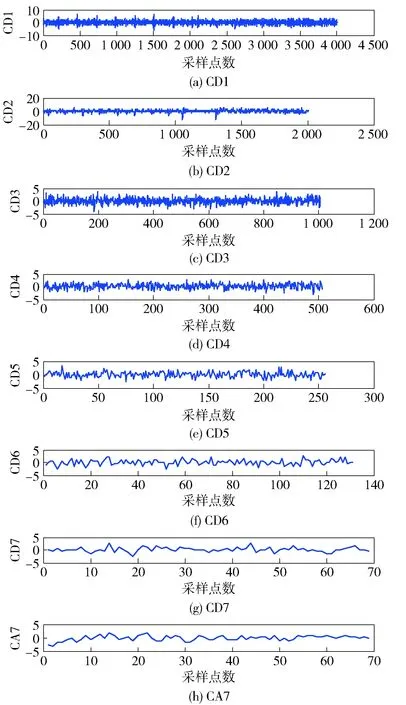
图5　小波分析提取的信号细微特征信息Fig.5　Detail feature information extracted by wavelet analysis

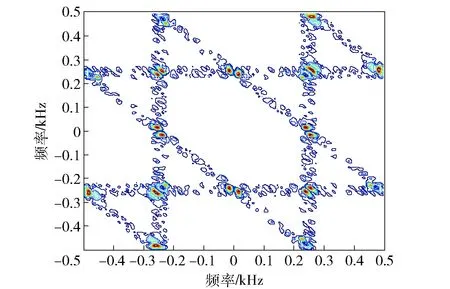
图6　信号的双谱特征Fig.6　Bispectral feature of signal

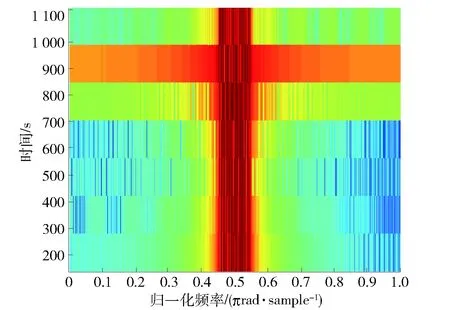
图7　信号的光谱特征Fig.7　Spectral feature of signal

如表5所示，由于人为干扰和背景噪声等因素，各个传感器获得的特征信息或多或少都会存在偏差，单独由一个传感器信息m1、m2和m3并不能准确实现对目标辐射源的识别，其获得的信息对识别框架内各个目标的支持度差异不够明显。本文提出的多源信息融合识别算法通过对多个传感器信息的融合实现对不确定信息的削弱，得到融合后的证据m如表5所示。融合后的证据m能够增强证据体对正确目标的支持程度，相对地降低了对其他对象的支持度，从而实现对目标信号准确识别。

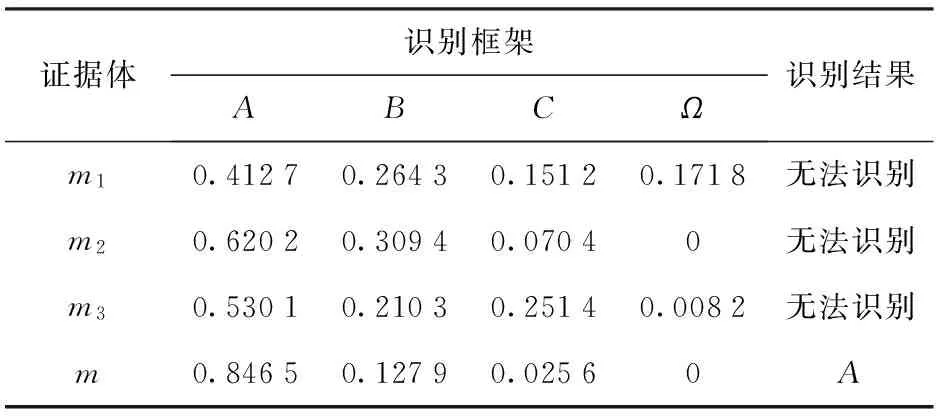
表5　目标识别体系中的BPA值

在实际情况下，不同传感器得到的侦测数据间的冲突程度通常并不会特别高，但同时各个mass函数之间的差异度并不能很好支持对目标个体的准确识别。因此只靠现有个体识别算法往往并不能实现理想的识别效果，而本文提出的融合识别算法能够最大限度地减少单一传感器所受的干扰和自身误差对识别结果产生的不利影响，提高了识别算法的鲁棒性和正确识别率。

4　结论

本文提出一种基于多传感器信息融合的通信辐射源个体识别方法，该方法可以根据所得证据的冲突程度自适应选择合适的融合方法。这样不仅保证了识别算法的正确识别率，同时也保证了算法的运算效率和合理性。通过仿真结果和分析可以得到以下结论：

1)与其他融合规则相比，本文基于决策向量的自适应证据融合方法具有更好的合理性和稳定性，能够综合考虑融合结果的准确性和高效性，在二者之间达到平衡。

2)本文提出的多元信息融合识别方法能够将各个传感器的侦察数据和已有的识别信息通过证据理论融合起来，有效提高了通信辐射源个体识别算法的正确识别率，并增强了算法的鲁棒性。

3)通过仿真分析可知，同现有的通信个体识别算法相比，本文提出的识别算法可以通过融合多源传感器信息减少人为干扰和背景电磁信号等不利因素对识别结果的影响。

References)

[1]张旻, 钟子发, 王若冰. 通信电台个体识别技术研究[J]. 电子学报, 2009, 37(10): 2125-2153.

ZHANG Min, ZHONG Zi-fa, WANG Ruo-bing. Research on the technique of individual communication transmitter identification[J]. Acta Electronica Sinca, 2009, 37(10): 2125-2153.(in Chinese)

[2]李程, 王伟, 施龙飞, 等. 基于多源信息融合的有源雷达组网方式序贯识别方法[J]. 电子与信息学报, 2014,36(10):2456-2463.

LI Cheng, WANG Wei, SHI Long-fei, et al. Sequential method for netting type recognition of active radars based on multi-source information fusion[J]. Journal of Electronics & Information Technology, 2014, 36(10):2456-2463.(in Chinese)

[3]张美璟, 王应明. 基于扩展原理的混合型证据推理不确定决策方法[J]. 控制与决策, 2015, 30(4): 670-676.

ZHANG Mei-jing, WANG Ying-ming. Hybird evidential reasoning for decision making under uncertainty based on extension principle[J]. Control and Decision, 2015, 30(4):670-676.(in Chinese)

[4]康兵义, 李娅, 邓勇, 等. 基于区间数的基本概率指派生成方法及应用[J].电子学报, 2012, 40(6):1092-1096.

KANG Bing-yi, LI Ya, DENG Yong, et al. Determination of basic probability assignment based on interval numbers and its application[J]. Acta Electronica Sinica, 2012, 40(6):1092-1096.(in Chinese)

[5]Han D Q, Deng Y, Han C Z. Novel approaches for the transformation of fuzzy membership function into basic probability assignment based on uncertain optimization[J]. International Journal of Uncertainty, Fuzziness and Knowledge-based Systems, 2013, 21(2):289-322.

[6]权文, 王晓丹, 王坚, 等.一种基于置信最大熵模型的证据推理方法[J]. 控制与决策, 2012, 27(6):899-903. QUAN Wen, WANG Xiao-dan, WANG Jian, et al. A combination rule of evidence theory based on brief max-entropy model [J].Control and Decision, 2012, 27(6):899-903. (in Chinese)

[7]Yang Y, Han D Q, Han C Z. Discounted combination of unreliable evidence using degree of disagreement[J]. International Journal of Approximate Reasoning, 2013, 54(8): 1197-1216.

[8]徐琰珂, 梁晓庚, 贾晓洪. 利用模糊证据理论的信息融合方法及其应用[J]. 哈尔滨工业大学学报, 2012, 44(3):107-111.

XU Yan-ke, LIANG Xiao-geng, JIA Xiao-hong. Information fusion based on fuzzy evidence theory and its application in target recognition[J]. Journal of Harbin Institute of Technology, 2012, 44(3):107-111.(in Chinese)

[9]韩德强, 杨艺, 韩崇昭. DS证据理论研究进展及相关问题探讨[J]. 控制与决策, 2014,29(1):1-11.

HAN De-qiang, YANG Yi, HAN Chong-zhao. Advances in DS evidence theory and related discussions[J]. Control and Decision, 2014, 29(1): 1-11.(in Chinese)

[10]邓勇, 施文康, 朱振福. 一种有效处理冲突证据的组合方法[J]. 红外与毫米波学报, 2004, 23(1):27-32.

DENG Yong, SHI Wen-kang, ZHU Zhen-fu. Efficient combination approach of conflict evidence[J]. Journal of Infrared and Millimeter Waves, 2004, 23(1):27-32.(in Chinese)

[11]蒋雯, 吴翠翠, 贾佳, 等. D-S证据理论中的基本概率赋值转换概率方法研究[J]. 西北工业大学学报, 2013, 31(2):295-299.

JIANG Wen, WU Cui-cui, JIA Jia, et al. A probabilistic transformation of basic probability assignment in D-S evidence theory[J]. Journal of Northwestern Polytechnical University, 2013, 31(2):295-299.(in Chinese)

[12]Donoho D L, Johnstone I M. Ideal spatial adaptation by wavelet shrinkage [J]. Biometrika, 1994, 81(3):425-455.

[13]Wei Y C. A novel D-S combination method of conflicting evidences based on Pearson correlation coefficient[J]. Telecommunication Engineering, 2012, 52(4):466-471.

[14]Yager R R. On the Dempster-Shafer framework and new combination rules[J]. Information System, 1989, 41(2):93-137.

[15]Pang J F, Lin Y, Li Y B, et al. A new DS evidence fusion algorithm based on cosine similarity coefficient[C]∥2013 International Conference on Measurement, Information and Control. Harbin, Heilongjiang: IEEE, 2013:1487-1490.

[16]孙权, 叶秀清, 顾伟康. 一种新的基于证据理论的合成公式[J]. 电子学报, 2000, 28(8):117-119.

SUN Quan, YE Xiu-qing, GU Wei-kang. A new combination rules of evidence theory[J]. Acta Electronica Sinica, 2000, 28(8):117-119.(in Chinese)

Individual Communication Transmitter Identification Based on Dempster-Shafer Evidence Theory

GUO Xiao-tao, WANG Xing, ZHOU Dong-qing

(Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, Shaanxi, China)

A novel multi-sensor information fusion identification method is proposed for the low accurate rate of the transmitter individual identification caused by the various jamming signals and sensor error, which can enhance the stability and accurate recognition rate of the transmitter individual identification in the complicated environment. The proposed method integrates the Dempster-Shafer evidence theory and feature extraction to get the utmost out of feature information and decrease the influence of uncertain factors in the signal processing. The features are extracted from the detected signals. The self-adaptive fusion rule based on the decision vector is utilized to fuse the evidences transformed by features. The recognition results can be obtained by judgment rules. The simulation analyses of self-adaptive fusion rule and fusion identification method are performed, respectively. The results show that the self-adaptive fusion rule can achieve a great balance between computational efficiency and accurate identification rate. Compared with other identification methods, the proposed fusion identification method can provide more accurate and stable recognition results.

ordnance science and technology; emitter identification; information fusion; Dempster-Shafer evidence theory; feature extraction; self-adaptive evidence fusion

2016-02-02

航空科学基金项目(20152096019、20145596025)

郭晓陶(1992—)，男，硕士研究生。E-mail：guoxiaotao526@163.com；

王星(1965—)，男，教授，博士生导师。E-mail：wx0944@163.com

TN911.72

A

1000-1093(2016)10-1844-08

10.3969/j.issn.1000-1093.2016.10.011