基于模糊决策图与灰色关联分析的枪械设计方案评价

阎艳， 郝佳， 陈中明， 王国新， 沙金龙

(1.北京理工大学 机械与车辆学院, 北京 100081; 2.北京机械电气研究所, 北京 102202)



基于模糊决策图与灰色关联分析的枪械设计方案评价

阎艳1， 郝佳1， 陈中明1， 王国新1， 沙金龙2

(1.北京理工大学 机械与车辆学院, 北京 100081; 2.北京机械电气研究所, 北京 102202)

为了解决产品设计方案评价指标相互影响的问题，提出了一种基于模糊决策图(FDM)与灰色关联分析(GRA)的方案评价方法(FDM-GRA)。该方法将GRA作为评价主体过程，利用模糊认知图表达指标间的影响关系，利用FDM实现指标赋权，通过计算灰色关联度来确定最优方案。该方法弥补了GRA无法表示评价指标之间相互影响的缺点。以枪械设计方案评价为例，验证了该方法的可行性。

兵器科学与技术； 方案评价； 评价指标； 相互影响； 模糊决策图； 灰色关联分析

0　引言

方案评价是枪械设计过程的重要的步骤，该步骤属于多目标决策(MADM)问题。实现方案评价的方法包括层次分析法(AHP)[1]、数据包络分析(DEA)[2]和灰色关联分析(GRA)[3]等。这些方法往往包含指标相互独立的假设。然而，MADM问题中的多个指标往往不相互独立，例如射击精度与成本之间存在影响关系。因此，这种假设会降低评价结果的可靠性。如何在评价方法中考虑评价指标间的影响关系是枪械设计方案评价必须考虑的问题。

目前，学术和工程领域普遍采用网络分析法(ANP)或决策试验与评价实验室(DEMATEL)分析法研究指标间的关系。例如，文献[4]将ANP应用于物流服务供应商的选择问题，有效地表达评价指标之间的影响关系；文献[5]利用ANP构建了供应商评价的依存、反馈网络，并对机床厂的4个供应商进行了评价。文献[6]利用DEMATEL分析法对房地产代理的服务质量进行评价；文献[7]在梳理了影响政府隐性知识共享的因素之后，利用DEMATEL方法确定了各影响因素的内在关系。此外，文献[8]结合ANP与DEMATEL方法，建立的方案评价方法用于企业的知识管理策略选择；文献[9]应用DEMATEL-ANP方法解决了水电施工现场安全评价问题。该方法以DEMATEL方法计算评价指标之间的影响强度，以ANP和混合权重进行不同评价指标的关联度排序，最后以因果图对评价指标进行分类分析，得到合理化建议。虽然ANP与DEMATEL方法可以表达指标间的影响关系，但只是表达了评价指标两两之间的直接影响关系，而难以表达指标间影响关系的传递效应。因此，研究评价指标间综合影响关系的表示方法，以及相应的方案评价方法是亟待解决的问题。为此，本文提出一种结合模糊决策图(FDM)与GRA的方案评价方法(FDM-GRA)。

1　相关研究

1.1模糊决策图

FDM[10]的核心思想是：评价指标之间的相互影响会导致单个评价指标对于总目标的重要程度发生变化。“总目标”是指方案评价的最终目的，如“好的枪械设计方案”。而对总目标而言，“全枪质量”、“故障率”和“经济成本”等指标所占的权重是不同的。例如，在评价指标相互独立的前提下，上述3个指标分配的权重分别为50%、30%、20%，则表示“全枪质量”对于一个“好的枪械设计方案”的影响最大，而“经济成本”这一指标却并不十分重要。然而，在实际的方案评价中，指标之间不是独立的。为此，首先给出如下定义：

定义1局部权重：未考虑评价指标之间的相互影响时，每一个评价指标对于总目标的重要程度，用z来表示。

定义2全局权重：考虑评价指标之间的相互影响时，每一个评价指标对于总目标的重要程度，用w来表示。

FDM的最终目的是计算全局权重，而全局权重则是由局部权重融合指标间的相互影响得到的。因此，全局权重的获取分为3个步骤：1)获取局部权重；2)获取指标间的相互影响关系；3)计算全局权重。其中，FDM是计算全局权重的关键。

模糊认知图(FCM)是一种由节点和带权重的有向边组成的网状图[11]。FCM可由4元组(N,E,C,f)来表示。其中：

N=(N1,N2,…,Nn)代表FDM中的节点；

E:(Ni,Nj)→eij是任意两个节点Ni、Nj之间有向连线的权重，即二者之间的相互影响关系。特殊的情况，如果i=j. 则eij=0. (eij)∈En×n代表影响矩阵；

C:Ni→Ci代表着节点Ni在给定时刻t时的状态值；

f代表阈值函数。该函数用于FCM的迭代运算，其目的是保证迭代后每一个节点的状态值都在可解释区间内。

C(t+1)=f(C(t)E),C(0)=In，

(1)

式中：In代表单位向量；C(0)称为初始向量，经过t次迭代后，C达到稳态。稳态下的各节点的状态值组成的矩阵C*称为稳态向量。

1.2灰色关联分析

GRA由4个步骤组成：构建指标矩阵、灰色关联生成、灰色关联系数计算和灰色关联度计算。各步骤具体的计算过程阐述如下。

1.2.1构建指标矩阵

假设有n个备选方案，m个评价指标。则评价指标矩阵可表示为

(2)

式中：xij表示第i个备选方案的第j个评价指标的值。

1.2.2灰色关联生成

由于评价指标具有不同的单位和数量级，需要对其进行等极化处理和归一化处理。等极化处理将具有不同极性的评价指标全部转换为极大型。评价指标的极性分为极大型(得分值越大越优)，极小型(得分值越小越优)和适中型(得分值取适中值为最优)。归一化处理将所有得分值转化为[0,1]之间的数值。

对于极大型指标，其等极化处理公式为

(3)

对于极小型指标，其等极化处理公式为

(4)

对于适中型指标，其等极化处理公式为

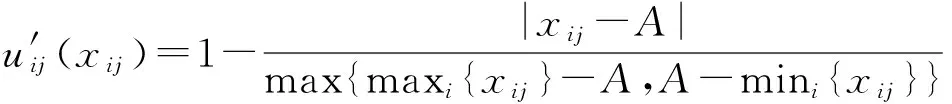
(5)

式中：A为适中值，一般可用序列平均值代替。

经过等极化处理后得到的矩阵称为等极化矩阵。在此基础上，进行归一化处理得到决策矩阵为

(6)

决策矩阵中的各评价值uij具有如下特征：1)所有评价值均处于[0,1]之间；2)所有评价值均是越大越优；3)经过灰色关联生成之后，各备选方案在各评价指标下的表现优劣可以直接通过比较其评价值的大小来判断。

1.2.3灰色关联系数计算

首先计算差值矩阵Δ，计算公式为

Δij=|x0j-xij|.

(7)

随后在差值矩阵Δ中找出Δmax和Δmin. 则uij与u0j之间的灰色关联系数εij可由公式(8)计算：

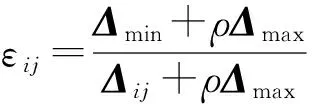
(8)

式中：ρ为分辨系数，其作用是扩展或压缩灰色关联系数的范围，通常取ρ=0.5.

1.2.4灰色关联度计算

基于灰色关联系数，方案的灰色关联度则可通过(9)式计算得出：

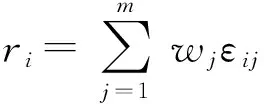
(9)

式中：wj代表各评价指标的权重，评价人员可依据需要为评价指标赋予不同的权重。

2　FDM-GRA方案评价方法

本文提出一种融合FDM与GRA的方案评价方法，该方法将FDM所得到的评价指标的全局权重w作为灰色关联度计算中的指标权重系数wj. 整体方法的流程如图 1所示。

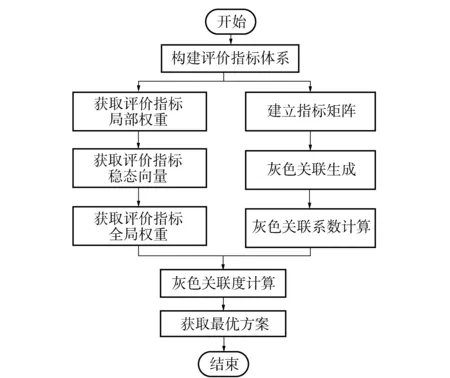
图1　FDM-GRA方法评价流程Fig.1　FDM-GRA evaluation process

FDM-GRA方案评价方法各步骤如下：

步骤1构建方案评价指标体系。针对具体问题确定方案评价的总目标及评价指标体系。假设针对某一方案评价问题，总目标为“综合最优的方案”；共有m个评价指标，则该方案评价问题的评价指标向量为Y=[y1,y2,…,yj,…,ym]，其中yj代表第j个评价指标。

步骤2构建局部权重矩阵Z. 基于方案评价指标体系，请专家两两比较评价指标对于总目标的重要程度，得到局部权重矩阵Z：

(10)

式中：zjk代表评价指标yj相对于评价指标yk对于总目标的重要程度。因此，zjj=1，zjk与zkj的值互为倒数。

步骤3计算局部权重zj. 计算局部权重矩阵的特征向量，此特征向量中的每一个值zj即为评价指标yj的局部权重。

步骤4构建评价指标的FDM. 请专家对方案评价指标之间的影响关系进行判断，并为影响关系赋权，得到方案评价指标的FDM.

步骤5将影响关系转换为影响矩阵E. 根据步骤4所得的评价指标FDM，将评价指标间的影响关系转换为影响矩阵E：

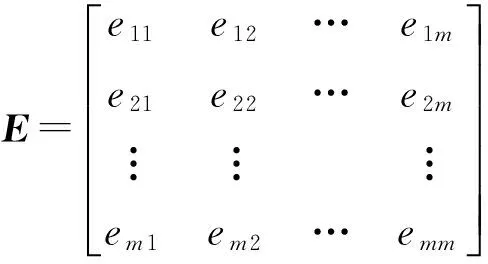
(11)

式中： ejk代表评价指标yj对评价指标yk的影响，ejk∈[-1,1]，特殊情况，当j=k时，即ejj=0.

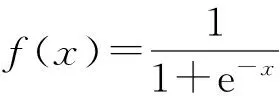
步骤7通过(12)式计算全局权重w*：

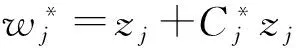
(12)

步骤8通过(13)式进行归一化处理。该全局权重wj即为计算灰色关联度时的权重系数。

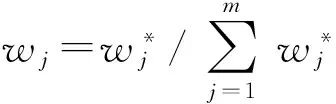
(13)

步骤9构建指标矩阵。设有n个备选方案。根据评价指标体系，请评价人员为每一个备选方案进行打分。如果是定量指标，则评分为具体的数值；如果是定性指标，则可根据具有要求来确定评分范围(如1～10)为备选方案评分，分值越高代表该备选方案在此评价指标下的表现越好。从而建立指标矩阵X：

(14)

式中：xij表示第i个备选方案在第j个评价指标下的评价值。

步骤10灰色关联生成。根据(3)式、(4)式、(5)式对矩阵进行等级化处理。经过等极化处理后得到的矩阵称为等极化矩阵：随后对等极化矩阵进行归一化处理，得到的矩阵称为决策矩阵。

步骤11灰色关联系数计算。在决策矩阵的基础上，根据(7)式、(8)式计算各个评价方案的灰色关联系数。

步骤12灰色关联度计算。在全局权重及灰色关联系数的共同基础上，利用灰色关联度计算(9)式计算出各项备选方案的灰色关联度。

步骤13获取最优方案。对备选方案的灰色关联度进行排序，数值最大者为最优方案。

3　验证实例

3.1验证过程

以枪械设计方案评价为例，验证本文所提出的FDM-GRA方案评价方法。现有4项备选枪械设计方案A、B、C、D，具体如下：

方案A.整体评价为质量小，射击精度很低，但结构复杂，故障率高。其中，全枪质量(不含枪弹)3.2 kg，100 m单发精度3.7 cm，故障率1.16%.

方案B.整体评价为质量小，射击精度低，故障率低，具有良好的安全性。其中，全枪质量(不含枪弹)3.6 kg，100 m单发精度4.3 cm，故障率0.07%.

方案C.整体评价为质量大，射击精度较高，故障率低，具有良好的安全性。其中，全枪质量(不含枪弹)3.9 kg，100 m单发精度5.4 cm，故障率0.16%.

方案D.整体评价为质量大，射击精度较高，维修性好，具有较高的安全性。其中，全枪质量(不含枪弹)3.8 kg，100 m单发精度4.9 cm，故障率0.05%.

利用FDM-GRA方法对如上4项备选方案进行评价，步骤如下：

步骤1构建方案评价指标体系。结合专家意见，给出如表1中7个评价指标。

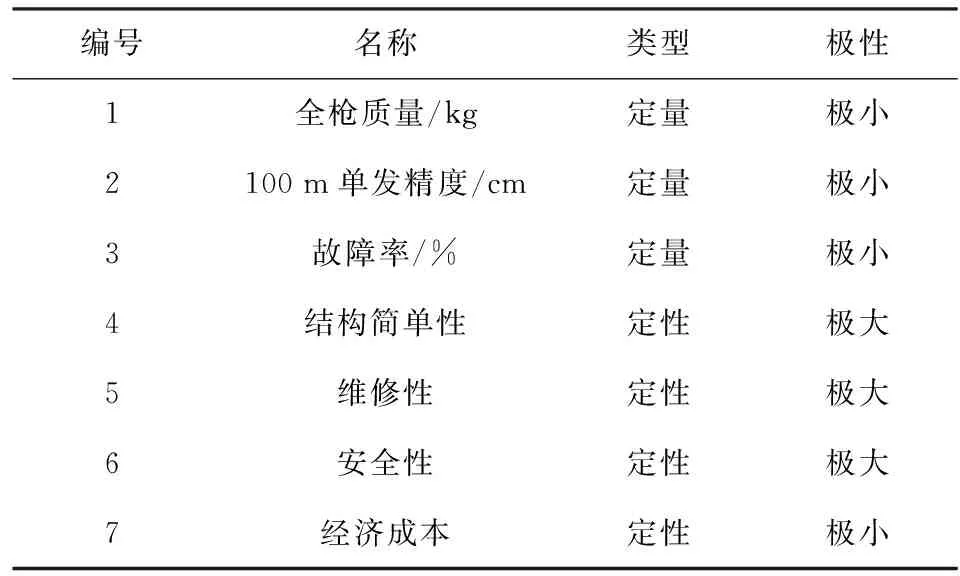
表1　枪械方案评价指标

步骤2构建局部权重矩阵Z. 两两对比各个评价指标对于总目标的重要程度，得到局部权重矩阵如表 2所示。

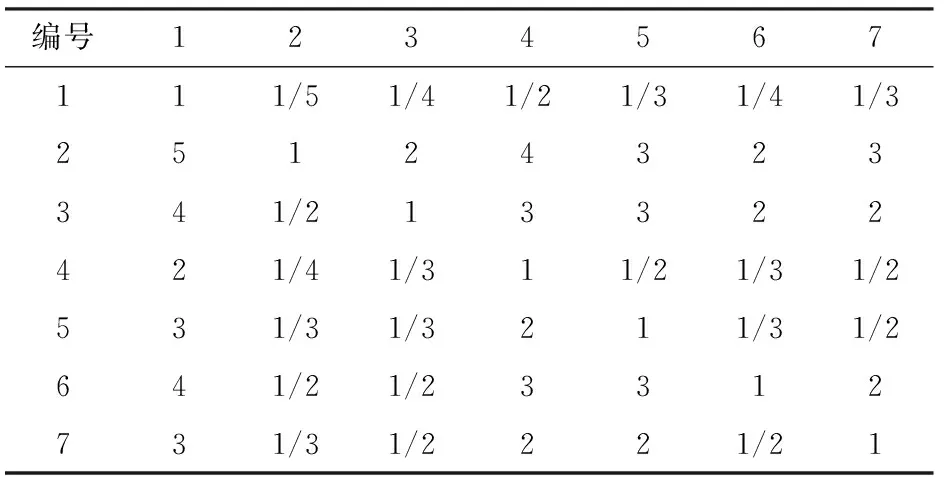
表2　局部权重矩阵

步骤3计算局部权重zj. 计算表2中矩阵的特征向量，得到局部权重zj分别为[0.093 9，0.677 0，0.492 7，0.142 4，0.196 6，0.402 7，0.262 7]。

步骤4构建FDM. 请枪械领域专家对评价指标之间的关系进行判断并赋权，得到枪械设计方案评价指标的FDM如图2所示。

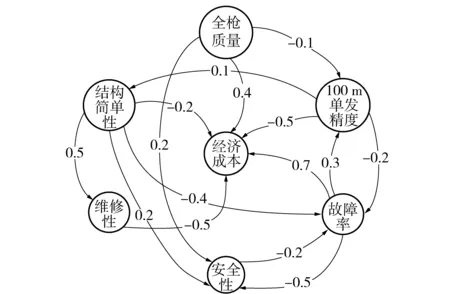
图2　枪械设计方案评价指标FDMFig.2　　　　Fuzzy decision maps of evaluation indexes of small arms design scheme

步骤5将影响关系转换为影响矩阵E. 根据图2将枪械评价指标间的影响关系转换为影响矩阵为

(15)

步骤6通过迭代运算得到稳态向量。 取阈值函数为Logistic函数，通过(1)式进行迭代运算，得到稳态向量为C*=(0.500 0,0.517 4,0.399 2,0.512 9,0.563 8,0.500 7,0.459 2).

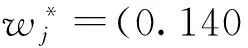
步骤9构建指标矩阵。请专家对4项备选方案的7个指标进行评价，得到评价指标矩阵如表3所示。

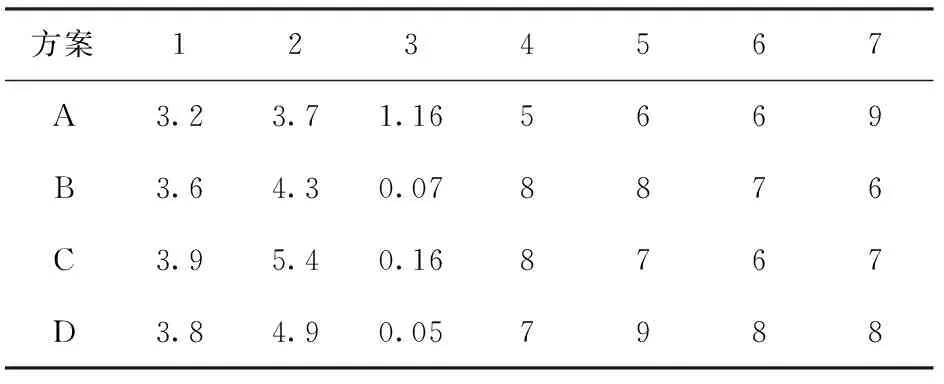
表3　枪械设计方案评价指标矩阵

步骤10灰色关联生成。按照(3)式、(4)式对指标矩阵进行等极化处理。例如，对于全枪质量而言，最大值来自方案C，为3.9；最小值来自方案A，为3.2. 由于属于极小型评价指标，应采用(3)式，对于方案B的指标值3.6所进行的处理为(3.9-3.6)/(3.9-3.2)=0.428 6. 对所有指标值进行等极化处理后所得的等极化矩阵如表4所示。

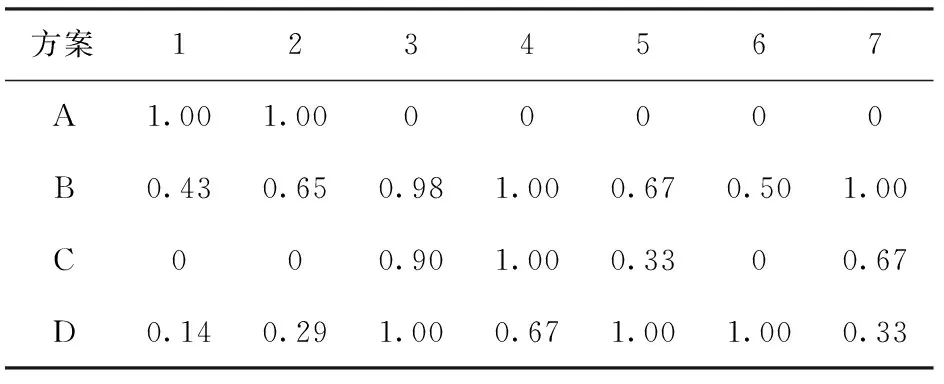
表4　等极化矩阵

经过归一化处理后所得的决策矩阵如表5所示。

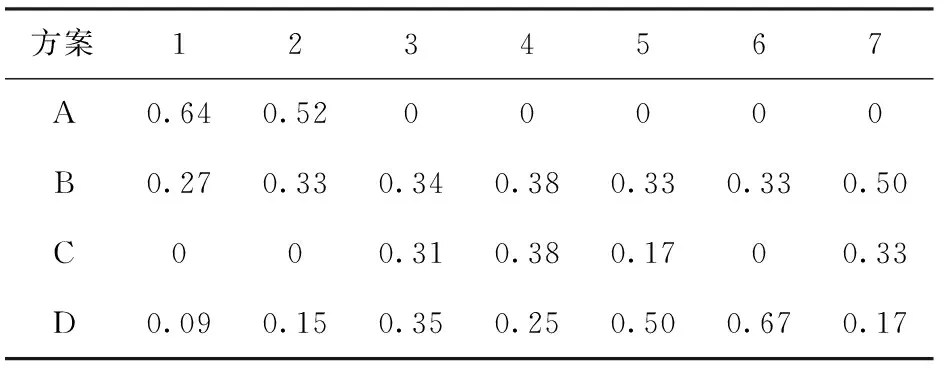
表5　决策矩阵

步骤11灰色关联系数计算。在决策矩阵的基础上，基于最优参考序列U0=(u01,u02,…,u0m)=(1,1,…,1)，利用(7)式计算所得的差值矩阵Δ如表6所示。

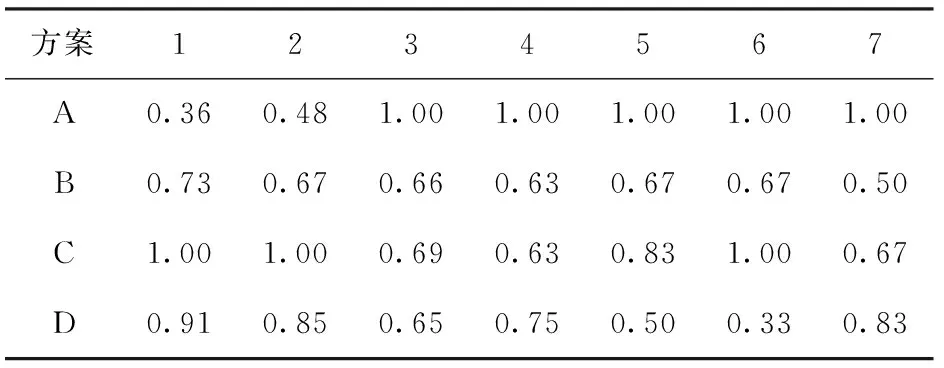
表6　差值矩阵

在表6中，Δmax=1.00，Δmin=0.33. 则经过(8)式计算得灰色关联系数如表7所示。

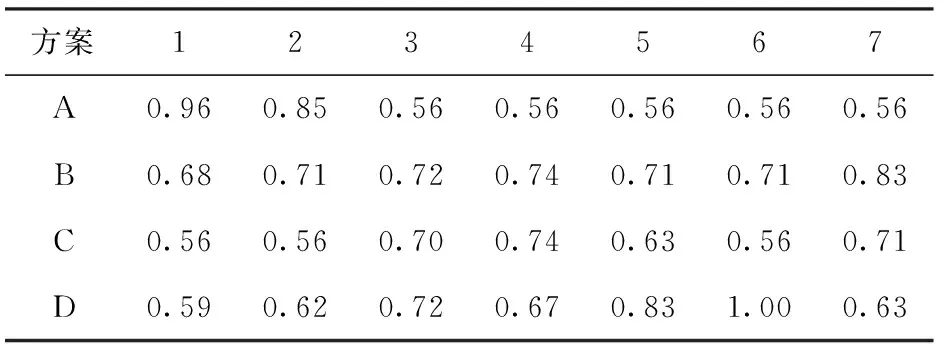
表7　灰色关联系数

步骤12灰色关联度计算。将步骤11所得的灰色关联系数与步骤8所得的全局权重带入(9)式中，计算出各备选方案的灰色关联度为R=(0.661 3，0.728 9，0.621 7，0.730 4)。

步骤13获取最优方案。4个方案的灰色关联度大小排序为0.730 4>0.728 9>0.661 3>0.621 7. 因此，各备选方案的最终排序为D>B>A>C，即方案D为最优方案。

3.2验证结果讨论

以上4个方案中，方案D虽然质量较大，射击精度在4项备选方案中只排在第3位，但其拥有最低的故障率，较高的结构简单性，最好的维修性与安全性，较低的经济成本。该实例中，专家对于故障率、安全性和经济成本都赋予了较高的权重。因此综合而言选择方案D为最优方案是合理的。

而方案C在专家最关注的100 m单发射击精度、故障率、安全性和经济成本这4项评价指标中都处在靠后的位置，因此被评价为最差的备选方案也是合理的。

为了进一步验证FDM-GRA方法的有效性，利用独立的GRA作为对比。

通过(9)式可知，各备选方案的灰色关联度由权重系数wj和灰色关联系数εij的乘积之和得到。如果独立应用GRA, 则wj值可均取为1(表示评价指标相互独立且权重相等)。仍以表7所得的灰色关联系数为数据基础，若wj=1，则代入(9)式，最终所得灰色关联度为R=(4.588 7，5.114 5，4.448 3，5.056 8)。

各方案的最终排序会变为B>D>A>C，即方案B成为了最优方案。GRA方法与FDM-GRA方法所得结果不一致。这种不一致是由于引入了全局权重。

4　结论

本文针对方案评价中评价指标相互影响的问题，提出一种基于FDM-GRA的方案评价方法。该方法以GRA为评价主体方法，以FDM获取各评价指标的全局权重，该全局权重通过局部权重、FDM和权重方程表达指标之间的综合影响关系。形成了考虑评价指标综合影响关系的方案评价方法。通过枪械设计方案评价的实例验证了该方法的可行性。

References)

[1]程庆文，汪波. 基于AHP和模糊理论的企业经营能力评价体系[J]. 系统工程与电子技术,2015, 37(1): 123-127.

CHENG Qing-wen, WANG Bo. Enterprise management capability evaluation based on AHP and fuzzy theory[J]. Systems Engineering and Electronics, 2015, 37(1): 123-127. (in Chinese)

[2]Azadi M, Jafarian M，Saen R F. A new fuzzy DEA model for evaluation of efficiency and effectiveness of suppliers in sustainable supply chain management context[J]. Computer & Operation Research, 2015, 54(C):274-285.

[3]戴小玲，唐明董，吕赛霞. 基于灰色关联分析的Web服务选择[J]. 计算机工程与科学, 2016, 38(2):297-304.

DAI Xiao-ling, TANG Ming-dong, LYU Sai-xia. Web service selection based on grey correlation analysis[J]. Computer Engineering & Science, 2016, 38(2):297-304. (in Chinese)

[4]Jharkharia S, Shankar R. Selection of logistics service provider: an analytic network process (ANP) approach [J]. Omega-International Journal of Management Science, 2007, 35(3): 274-289.

[5]白朝阳，张冠男，沈灵丽. 基于网络层次分析法(ANP)的机床行业重点商业型供应商评价方法研究[J]. 制造业自动化, 2014,36(1):146-151.

BAI Zhao-yang, ZHANG Guan-nan, SHEN Ling-li. The evaluation of key business supplier in machine tool industry based on the network analytic hierarchy process (ANP) [J]. Manufacturing Automation, 2014, 36(1): 146-151. (in Chinese)

[6]Tseng M L. A causal and effect decision making model of service quality expectation using grey-fuzzy DEMATEL approach [J]. Expert Systems with Applications, 2009, 36(4): 7738-7748.

[7]陈福集, 介静涛. 网络舆情管理中政府隐性知识共享因素分析[J]. 情报杂志, 2014,33(5):148-152.

CHEN Fu-ji, JIE Jing-tao. Government tacit knowledge sharing factors analysis in internet public opinion management [J]. Journal of Intelligence, 2014, 33(5):148-152. (in Chinese)

[8]Wu W W. Choosing knowledge management strategies by using a combined ANP and DEMATEL approach [J]. Expert Systems with Applications, 2008, 35(3):828-835.

[9]裴金勇,曾伟,李莹，等. 基于 DEMATEL-ANP 水电施工现场安全评价模型研究[J]. 中国安全生产科学技术, 2012,8(7):89-93.

PEI Jin-yong, ZENG Wei, LI Ying, et al.Research on safety assessment model of hydroelectric construction site with DEMATEL and ANP[J]. Journal of Safety Science and Technology, 2012, 8(7): 89-93. (in Chinese)

[10]Yu R, Tzeng G H. A soft computing method for multi-criteria decision making with dependence and feedback[J]. Applied Mathematics and Computation,2006,180(1):63-75.

[11]Kosko B. Fuzzy cognitive maps [J]. International Journal of Man-Machine Studies, 1986,24(1):65-75.

Design Scheme Evaluation Based on Fuzzy Decision Maps and Grey Relational Analysis

YAN Yan1， HAO Jia1， CHEN Zhong-ming1， WANG Guo-xin1， SHA Jin-long2

(1.School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China; 2.Beijing Institute of Mechanics and Electronic, Beijing 102202, China)

A scheme evaluation method based on fuzzy decision maps and grey relational analysis is proposed to solve the problem of mutual influence of the design scheme evaluation indexes. The proposed method takes grey relational analysis as a main evaluation progress, and uses fuzzy cognitive map to represent the mutual influence of the evaluation indexes. The fuzzy decision maps are used to calculate the influence relationship among the evaluation indexes. The grey relational grades of all alternatives are calculated to determine the optimal scheme. The feasibility of the proposed method is verified by taking the design scheme evaluation of small arms for example.

ordnance science and technology; scheme evaluation; evaluation index; mutual influence; fuzzy decision maps; grey relational analysis

2015-08-05

国家自然科学基金项目(51375049、51505032)；国家部委基础科研项目(JCKY2016602B007)

阎艳(1967—)，女，教授，博士生导师。E-mail: yanyan331@bit.edu.cn；

郝佳(1984—), 男, 讲师。E-mail: haojia632@bit.edu.cn

TJ202

A

1000-1093(2016)10-1934-07

10.3969/j.issn.1000-1093.2016.10.021