基于小波包分形的瓦斯传感器故障诊断方法*

陈 宏，邓芳明，吴 翔，付智辉

(1.华东交通大学 轨道交通学院，江西 南昌 330013;2.华东交通大学 电气与自动化工程学院，江西 南昌 330013)



基于小波包分形的瓦斯传感器故障诊断方法*

陈 宏1，邓芳明2，吴 翔2，付智辉2

(1.华东交通大学 轨道交通学院，江西 南昌 330013;2.华东交通大学 电气与自动化工程学院，江西 南昌 330013)

针对瓦斯传感器的故障诊断问题，提出一种基于小波包分形的瓦斯传感器故障诊断方法。使用3层小波包对故障信号进行分解和重构，获得不同频带的重构信号，计算各个重构信号的分形维度，并构成对应的故障特征向量。以此作为输入向量来训练支持向量机(SVM)，完成故障的诊断。实验结果表明：该方法能有效地提取传感器的故障特征，提高了传感器故障诊断的准确率，可有效地应用于瓦斯传感器的故障诊断。

瓦斯传感器故障诊断； 小波包变换； 分形分析； 支持向量机

0 引 言

由于瓦斯传感器[1]长期处于高温、高湿度、高粉尘、强干扰的恶劣环境中，经常发生卡死、冲击、漂移、偏差和干扰等故障。

传统的传感器故障诊断方法有主成分分析(principal component analysis，PCA)[2,3]、小波变换及神经网络方法[4～7]。文献[2]使用PCA分解出信号的残差分量，通过判断残差分量是否超过预定阈值来判断故障情况，PCA属于简单线性统计方法，不适合处理包含多噪声及动态特征的故障情况。小波包变换同时对信号的低频和高频部分进行分解，具有很强的辨析力。文献[4]使用3层小波变换分解信号提取各频带的能量系数构成故障特征向量，诊断效果良好。然而基于频带能量的方法难以区分某些故障。文献[6]以神经网络方法取得了良好的效果，但神经网络需要大量的故障数据训练，而实际情况中传感器的故障数据往往很难大量获得。

分形理论可以有效地刻画和度量信号的复杂性和动态性。当瓦斯传感器发生故障，对应不同故障类型的输出信号会表现出不同的动态性、非平稳和不规则性。借助分形理论可以有效揭示故障信号的本质信息。支持向量机(support vector machine，SVM)是一种统计学习理论方法[8]，建立于结构风险最小化原理基础上,在模型的复杂性和学习能力间寻求最佳折中,对于小样本、非线性、多维度问题具有优异的泛化能力，有效地解决传感器小故障样本数据的训练问题。

本文提出一种基于小波包分形的瓦斯传感器故障诊断方法，实验结果表明：该方法可有效提取传感器的故障特征,提高了故障诊断准确率。

1 小波包变换和分形理论

1.1 小波包变换

小波包分析是小波分析的延伸，是一种对信号进行更细致分解和重构的方法。小波分析每次只对上级分解的低频部分进行分解，对高频部分不再分解。而小波包则同时对高低频部分进行分解，对细节的辨析力更强。对瓦斯传感器故障输出信号u(t)进行小波包分解的递归方程如下

(1)

式中 h(k)为高通滤波器组,g(k)为低通滤波器组。小波包分解的实质是让故障输出信号通过高低通滤波器组,递归分解成含有特定故障信息量的高频和低频部分。

1.2 分形理论

分形理论能有效地度量信号的复杂性和刻画相应的特征。而分形维数是度量和刻画信号复杂性的基本指标。本文使用Katz提出的信号分形维数计算法计算信号的分形维数。

(2)

1.3 基于小波包分形的故障特征向量提取

综上，基于小波包分形的瓦斯传感器故障特征向量的提取步骤为：

1)对传感器故障输出信号u(t)执行j层小波包分解，分别提取第j层的各分解序列Xjk，k=0,1,2,…,2j-1；

2)重构步骤(1)所得的小波包分解序列Xjk，得到相应的重构信号Sjk，各个重构信号包含了原始信号从低频到高频的信息；

3)根据式(2)分别计算各个重构信号Sjk的分形维数FDk，将所得结果构成一个故障特征向量，记为：F-[FD0,FD1,…,FD2j-1]。

2 SVM

WTφ(x)+b=1

(3)

式中 W和b为超平面的权值和偏置。φ(x)为映射函数，将数据从低维空间映射到高维空间。本文选用高斯径向基(RBF)函数作为核函数(σ为核参数)，满足

K(x,xi)=φ(x)·φ(xi)=exp(-‖x-xi‖2/2σ2)

(4)

最优分类超平面满足下述不等式约束条件

(5)

式中 C为惩罚因子,ξi为松弛变量。

求解上述最优化问题，解得W*和b*，则二分类支持向量机的决策函数为

(6)

传感器多故障模式的诊断属于多分类问题，需要将二分类SVM拓展为多分类SVM。多分类SVM的构建方法有一对一、一对多以及二叉树法。针对N分类问题，由于一对一SVM需要构建N(N-1)个二分类SVM，加重了训练耗时和诊断用时；而一对多SVM存在数据不对称问题，分类误差较大；而二叉树SVM只需N-1个二分类SVM，分类精度高和可靠。因此,本文选择二叉树SVM作为传感器多故障模式的诊断分类器。针对传感器常见的7类故障(包括正常模式)，本文构建了相应的二叉树SVM分类器，其示意图如图1所示。图中，F0～F6分别代表传感器的正常、偏差、冲击、漂移、周期性干扰、噪声干扰、卡死模式。方框代表SVM分类器，圆形代表故障类别。

图1 二叉树SVM分类器示意图Fig 1 Diagram of binary tree SVM classifier

3 实验设计和结果分析

3.1 实验设计

图2给出了基于小波包分形的瓦斯传感器故障诊断的基本流程图。

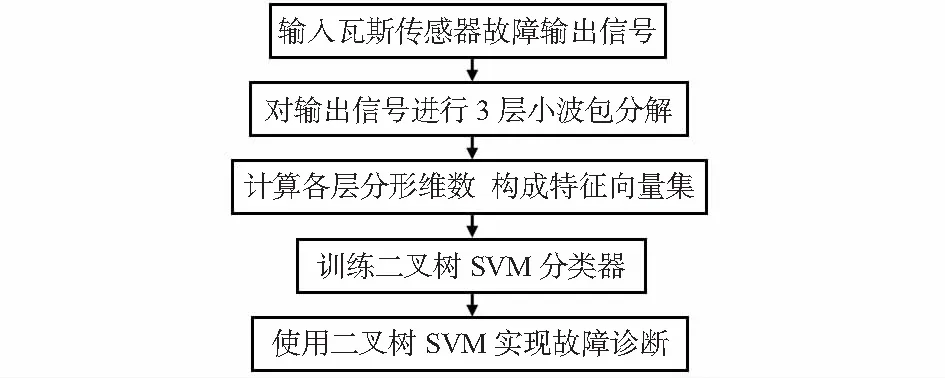
图2 瓦斯传感器故障诊断的基本流程图Fig 2 Basic flow chart of gas sensor fault diagnosis

本次实验以淮南矿业集团张北煤矿为背景，实验的研究对象为KG9017A低浓度甲烷传感器。从该煤矿的瓦斯数据库中获取该瓦斯传感器的正常、偏差、冲击、漂移、周期性干扰、噪声干扰和卡死等7种状态下的实测数据各60 组(采样率16 kHz，采样点数1 024点)。对每种状态模式，将其中的40组作为训练样本集，剩下的20组作为测试样本集。本文选择db4小波作为小波基函数，并执行3层db4小波包分解。

为了清楚地说明该瓦斯传感器故障特征向量的构成方法，图3给出了当瓦斯传感器发生冲击故障时，对一个故障输出信号进行3层小波包分解和重构，然后计算出其分形维数的示意图。从图3可见，9子图从上到下从左到右分别代表原始的故障输出信号和经小波包分解重构后的第3层从低频到高频的重构信号。对各个重构信号分别进行分形维数计算得到各自的分形维数为1.570 2,1.108 5,1.543 9,1.350 1,1.195 9,1.280 9,1.603 8,1.247 5，再将这8个分形维数组合成一个故障特征向量。根据相同的方法对传感器所有故障模式的输出信号进行小波包变换和分形维数计算并组合，即可得到所有的相应的故障特征向量集。表1给出了该瓦斯传感器不同故障模式下典型的特征向量值。

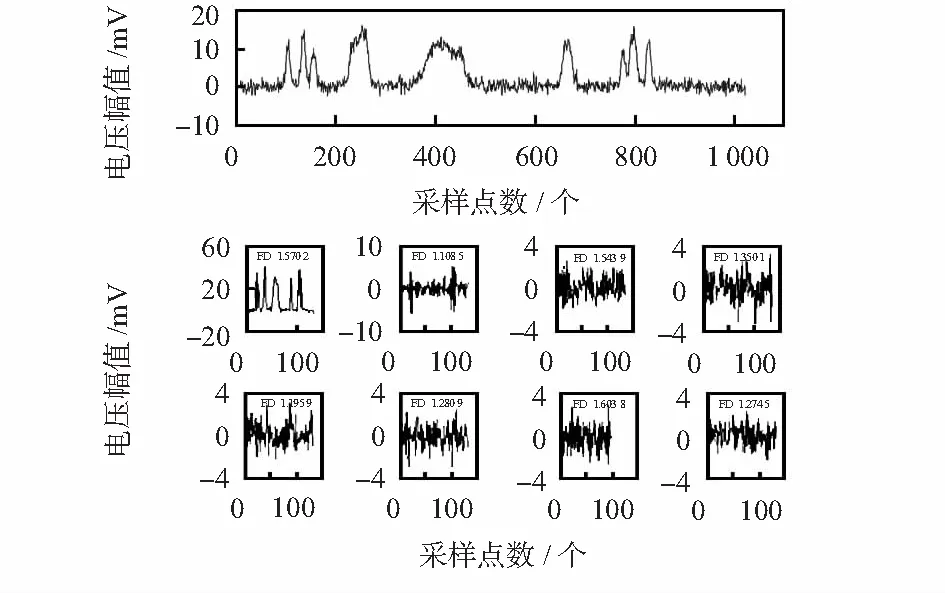
图3 瓦斯传感器故障特征向量的构成示意图Fig 3 Constitution diagram of fault feature vectors of gas sensor

3.2 结果分析

使用故障特征向量集对二叉树SVM继续进行训练，其中SVM的核参数和根据粒子优化(PSO)算法确定[9]。为了体现本文所提出方法的整体性能，本文选择与文献[2,6]

表1 传感器不同状态下的特征向量值

中的方法进行对比。表2给出了本文方法和其他方法的诊断结果的对比。从表2可见，本文基于小波包分形和支持向量机的瓦斯传感器诊断方法的总体准确率达到98.57 %，从整体上要优于文献[2,6]的方法，且在多种故障模式的辨识中均有满意的准确率。

表2 不同诊断方法的诊断结果对比

为了说明分形理论在提取传感器故障特征向量的优越性，本文选择与文献[6]中的特征提取方法作为对比，使用的分类器均为二叉树SVM(参数均经PSO算法优化)。表3给出两种特征提取方法的诊断结果对比。从表3可见，虽然两种故障特征向量提取方法均以小波包变换为基础，但小波包变换之后，基于分形维度的方法的总体准确率要高于基于频带能量的方法。并且对于偏移和卡死两种故障的辨识诊断，基于分形维数的方法的区分度更高。说明分形维数可以有效地刻画和度量信号的复杂度，揭示不同故障信号中隐含的特性。

表3 不同特征提取方法的诊断结果对比

为了进一步说明二叉树SVM在小样本情况下依然具有稳定的分类精度，本文选择与文献[6]中RBF神经网络分类器进行对比。其中，重新划分每种故障模式训练和测试集的比例，对每种故障模式，20组数据作为训练样本，40组作为测试样本，使用相同的方法提取故障特征。表4给出了小样本情况下不同分类器的诊断性能对比。从表4可见，当训练样本减少时，神经网络的诊断性能急剧下降，而二叉树SVM依旧保持较高的分类准确率，从而证明SVM在小样本情况下依然具有优异的诊断能力。

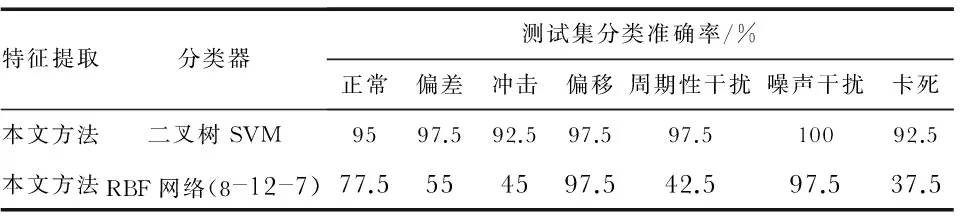
表4 小样本情况下的二叉树SVM与神经网络的分类性能对比

4 结 论

本文提出了一种基于小波包分形的瓦斯传感器故障诊断方法，该方法首先对瓦斯传感器故障输出信号执行3层db4小波包分解和重构，获得不同频带的重构信号，再计算各个重构信号的分形维度，并构成相应的故障特征向量，再使用二叉树SVM进行瓦斯传感器故障诊断分类。实验结果表明：1)本文基于分形理论的方法较基于频带能量的方法更有效地提取故障特征；2)二叉树SVM较神经网络在小样本情况下具有优异的诊断能力；3)本文所提方法诊断准确率高，能有效应用于瓦斯传感器故障诊断中。

[1] 王军号，孟祥瑞，吴宏伟.基于小波包与EKF—RBF神经网络辨识的瓦斯传感器故障诊断[J].煤炭学报,2011,36(5):868-872.

[2] 黄 丹,徐平安,王其军,等.基于PCA神经网络和D-S决策的瓦斯传感器故障辨识[J].仪表技术与传感器,2015(3):99-103.

[3] 胡顺仁,李瑞平,包 明,等.基于主元分析的桥梁挠度传感器故障诊断研究[J].传感器与微系统,2014,33(6):9-12.

[4] 赵金宪,金鸿章.基于小波包和神经网络的瓦斯传感器故障诊断[J].传感器与微系统,2010,29(5):80-82.

[5] 刘江利,陈 健,谢永兴.基于小波分析的浊度传感器故障诊断研究[J].传感器与微系统,2011,30(8):12-14.

[6] 单亚峰,孙 璐,付 华,等.基于小波包和RBF神经网络的瓦斯传感器故障诊断[J].传感技术学报,2015,28(2):278-283.

[7] 赵劲松,李 元,邱 彤.一种基于小波变换与神经网络的传感器故障诊断方法[J].清华大学学报：自然科学版,2013,53(2):205-209.

[8] 张学工.关于统计学理论与支持向量机[J].自动化学报,2000,26(2):32-34.

[9] 费胜巍,苗玉彬,刘成良,等.基于粒子群优化支持向量机的变压器故障诊断[J].高电压技术,2009,35(3):509-513.

邓芳明，通讯作者，E—mail:dengfm1980@sina.cn。

Gas sensor fault diagnosis method based on wavelet package fractal analysis*

CHEN Hong1,DENG Fang-ming2,WU Xiang2,FU Zhi-hui2

(1.School of Railway Tracks and Transportation,East China Jiao Tong University， Nanchang 330013,China;2.School of Electrical and Automation Engineering, East China Jiao Tong University，Nanchang 330013,China)

Aiming at fault diagnosis problem of gas sensor,a gas sensor fault diagnosis method based on wavelet package fractal analysis is proposed.Fault signals are decomposed and reconstructed by using three-level wavelet package,reconstructed signals of different frequency bands are achieved.Compute fractal dimension of each reconstructed signal,and compose corresponding fault feature vectors.Inputting these fault vectors to train SVM to achieve fault diagnose.Experimental result shows that the proposed method extract effectively features of fault of sensor and increase of fault diagnosis,which can be applied to fault diagnosis of gas sensor effectively.

gas sensor fault diagnosis;wavelet package transform;fractal analysis;support vector machine(SVM)

10.13873/J.1000—9787(2016)11—0026—04

2016—07—15

国家自然科学基金资助项目(21265006)；江西省科技支撑计划资助项目 (20161BBE50076,20161BBE50077)

TP 212

A

1000—9787(2016)11—0026—04

陈 宏(1967-)，男，江西南昌人，实验师，从事传感器技术和测量技术研究工作。