三维高频风速时间序列波动特性研究*

曾 明，李静海，张小内

(天津大学 电气与自动化工程学院，天津 300072)



三维高频风速时间序列波动特性研究*

曾 明，李静海，张小内

(天津大学 电气与自动化工程学院，天津 300072)

三维高频风速波动特性的研究对于全面、深入地揭示复杂风场流动及演化规律具有重要价值。采用多重分形消除趋势波动分析(MF—DFA)对高性能超声波风速传感器采集的三维风速时间序列进行波动特性分析。研究表明：水平风速和竖直风速均具有多重分形特性，但有着不同的波动结构，在竖直方向上的波动结构要更为复杂；水平方向风速信号的多重分形特性由长程相关性造成，与概率分布关系不大，而竖直方向上风速信号的多重分形特性与长程相关性和概率分布均存在一定的关联。

三维超声波风速传感器； 高频风速时间序列； 多重分形消除趋势波动分析； 多重分形谱

0 引 言

风场的流动及演化规律的研究成果在气象、农业、能源、环保等多个领域均蕴藏巨大的潜在应用价值，因此，该主题的研究受到了各国科研人员的广泛关注。柳亦兵等人[1]利用对数功率谱和频率之间的拟合关系确定了近地面风速具有非平稳特性。曾明等人[2]通过替代数据和饱和关联维数相结合的方法证明了近地面风场具有混沌特性。Chang T等人得出风速时间序列的分形维数与风速平均值成负相关。De Oliveira Santos M等人证明了时间尺度为小时的风速时间序列是长程幂律相关的。孙斌等人[3]证明了采用多重分形谱可在一定程度上对时间尺度为小时的风电场风速变化趋势进行预测。虽然已有了一些关于风场的分形分析结果，但研究的时间尺度较大，多为小时或天，同时分析对象大多仅限于二维风场数据。深入细致地解读近地面高频三维风场时间序列的波动特性，将有助于更好地掌握近地面风场的流动及演化规律，对于风场的精确建模及短时风场预测具有重要意义。

本文以高性能超声波风速传感器所测三维高频风速数据为对象，采用多重分形消除趋势波动分析(multifractal detrended fluctuation analysis,MF—DFA)方法从多重分形角度分析了时间尺度为秒级的三维高频风速竖直分量、水平分量与合成分量的波动特性。最后采用替代数据法对波动特性产生的机理进行了解读。

1 MF—DFA方法

Kantelhardt J W等人[4]最早提出的MF—DFA方法主要用于非线性非平稳时间序列分析。MF—DFA方法包括5个步骤：

1)对于长度为N的时间序列{xk,k=1,2,…，N}，构造去均值的和序列

(1)

2)将新序列Y(i)划分为长度为s的Ns个不相交的区间，其中,Ns=int(N/s)。由于N不总是能被s整除，为了保证序列Y(i)的信息在划分过程中不至于丢失，对Y(i)按i由小到大和由大到小各划分一次，这样，共得到2Ns个区间。

3)对每个区间v=1,2,…,2Ns内的s个点，用最小二乘法进行k阶多项式拟合

yv(i)=a0+a1i+…+akik,k=1,2,…,m

(2)

式中 ak(k=1,2,…,m)为多项式系数，m为去除趋势的阶次。

4)计算均方误差F2(s,v)

当v=1,2,…,Ns时

(3)

当v=Ns+1,Ns+2,…,2Ns时

(4)

5)对于2Ns个区间，求F2(s,v)的q阶均方根，进一步开方得到q阶波动函数

(5)

式中 q可取任意不为0的实数。特别地，当q=0时，需要对上式求极限，得到的波动函数为

(6)

式中 Fq(s)为关于时间尺度s和阶次q的函数，随着s增大，Fq(s)与s呈幂律关系，即

Fq(s)∝sh(q)

(7)

式中 h(q)称为广义赫斯特指数。当q=2时，h(2)也就是赫斯特指数H。当h(2)=0.5时，{xk}为一独立过程；当h(2)<0.5时，{xk}存在负长程相关性；当h(2)>0.5时，{xk}存在长程相关性。当时间序列为单分形时，h(q)为一个独立于q的常数；当时间序列为多重分形时，h(q)随q而变化。另外一种刻画多重分形时间序列特征的方法是分形奇异指数α和奇异谱f (α)，它们与广义赫斯特指数h(q)有如下关系

(8)

奇异指数α的大小决定着时间序列波动过程在局部上的不规则程度。多重分形谱f (α)则可以进一步反映信号奇异指数α的分布，奇异谱峰值处的奇异值α0(fmax=f (α0)，α0∈[αmin,αmax])表征时间序列的平滑或剧烈波动程度，奇异谱的宽度Δα=αmax-αmin表示多重分形强度。

2 三维高频风速时间序列采集

如图1所示,选用Gill R3—50型三维超声波风速传感器测量风场信号，传感器采样频率50 Hz，分辨率0.01 m/s，测量精度优于±1 %。将传感器放置在室外空旷地带测量三维风场数据，传感器距地面高度为0.3 m。通过多次实验，选取具有代表性的1 h(3 600 s)的三维风速数据，该风速数据包括x,y,z三个分量，其中,x和y为水平分量，z为竖直分量。用x,y,z三个分量按式(9)合成瞬时风速v,即

(9)

式中 N为时间序列长度。各分量的风速与合成风速如图2。

图1 高性能三维超声波风速传感器Fig 1 High property 3D ultrasonic anemometer

图2 风速时间序列vFig 2 Wind speed time sequence

3 实测高频风速时间序列分析

3.1 高频风速时间序列的多重分形特性

对图2中的风速时间序列进行MF—DFA分析，得到的广义赫斯特指数h(q)如图3(a)所示，多重分形谱f(α)如图3(b)所示。可以看出：1) 三维风速分量与合成风速的赫斯特指数H均大于0.5，广义赫斯特指数h(q)均随阶次q而变化，表明高频风速时间序列具有长程相关性和多重分形特性。2) 风速竖直分量的广义赫斯特指数随阶次的变化范围和多重分形谱宽度要远大于水平分量x,y以及合成风速v，奇异指数也最小，表明风速在竖直方向上的多重分形特性最强，波动特性也最为复杂。3)合成风速的广义赫斯特指数和多重分形谱与水平分量最为接近，表明合成风速的多重分形特性主要由水平分量而决定，受竖直分量影响较小。

图3 风速时间序列x,y,z和v的MF—DFA结果Fig 3 MF—DFA results of wind speed time sequence x,y,z and v

3.2 风速时间序列的替代数据分析

本节将用替代数据法来分析风速时间序列多重分形成因及其非线性特性。分析多重分形成因通常采用随机重排法。如果随机重排后多重分形谱不变，则多重分形特性由概率分布造成；如果随机重排序列变为随机序列，则多重分形特性由长程相关性造成；如果随机重排序列仍为多重分形，但多重分形强度弱于原始序列，则多重分形特性与概率分布和长程相关性都有关。探讨非线性特性一般采用相位随机化[5]，即先将原始信号进行傅里叶变换，变为频域信号后保持其幅值不变并将相位随机重排，然后再进行傅里叶反变换。如果原序列多重分形特性与非线性特性有关，在相位重排后多重分形特性会减弱；如果一个时间序列的多重分形特性与非线性特性无关，则相位重排对其多重分形特性无影响。替代数据分析结果如图4所示。

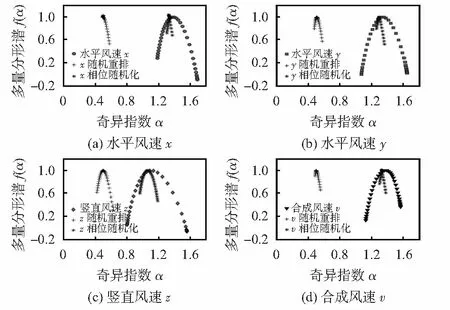
图4 替代数据分析结果Fig 4 Results of surrogate analysis

从图4可以看出：1) 随机重排以后，风速水平分量x,y与合成风速v的谱宽度由原来的0.5左右变为了0.1，表明水平风速与合成风速的多重分形特性是由长程相关性造成的，与概率分布关系很小；竖直分量的谱宽度在随机重排后虽然减小了，但依然还大于0.2，具有较弱的多重分形特性，表明竖直风速的多重分形特性不仅由长程相关性造成，还与概率分布有关。2)相位随机化以后，非线性特性减弱，风速水平分量、竖直分量与合成风速的多重分形强度也降低，表明风速的多重分形特性与其非线性特性有关。

4 结 论

本文采用MF—DFA方法分析了三维超声波风速传感器测得的高频风速时间序列，结果表明：水平风速和竖直风速均具有多重分形特性；风速的竖直分量与水平分量有着不同的波动结构，竖直方向上风速波动特性要更为复杂；水平方向风速的多重分形特性由长程相关性造成，与概率分布关系不大，而竖直方向上风速的多重分形特性与长程相关性和概率分布都有关。

[1] 柳亦兵，李 虎，马志勇，等.风速时间序列的非线性特性分析[J].华北电力大学学报，2008,35(6):99-102.

[2] Zeng M,Jia H Y,Meng Q H,et al.Nonlinear analysis of the near-surface wind speed time series[C]∥The 5th International Congress on Image and Signal Processing(CISP)，Chongqing,China：IEEE,2012:1893-1897.

[3] 孙 斌，姚海涛.风电场风速时间序列的多重分形去趋势波动分析[J].电工技术学报，2014,29(6):204-210.

[4] Kantelhardt J W,Zschiegner S A,Koscielny-Bunde E,et al.Multifractal detrended fluctuation analysis of nonstationary time serie-s[J].Physica A-Statistical Mechanics and its Applications,2002,316:87-114.

[5] Ivanov P C,Amaral L,Goldberger A L,et al.Multifractality in human heartbeat dynamics[J].Nature,1999,399(6735):461-465.

Study on fluctuation characteristics of 3D high-frequency wind speed time sequence*

ZENG Ming,LI Jing-hai,ZHANG Xiao-nei

(School of Electrical Engineering and Automation,Tianjin University,Tianjin 300072,China)

Study on fluctuation characteristics of 3D high-frequency wind speed time sequence has an important value for revealing the laws of complex wind field flow and evolution.Multifractal detrended fluctuation analysis(MF—DFA)is applied to analyze fluctuation characteristics of 3D wind speed time sequence measured by high-property ultrasonic anemometer.Research shows that both horizontal and vertical wind signals exhibit multifractal features,but have different fluctuation structures.Vertical fluctuation structures are much more complex than the horizontal ones.The multifractality in horizontal wind signals is due to the long-range correlations rather than the probability density.While long-range correlations and the probability density both affect on multifractality in vertical wind signal.

3D ultrasonic anemometer;high frequency wind speed time sequence;multifractal detrended fluctuation analysis(MF—DFA);multifractal spectrum

10.13873/J.1000—9787(2016)11—0030—03

2016—01—08

国家自然科学基金资助项目(61271321,61573253)

TP 212.9

A

1000—9787(2016)11—0030—03

曾 明(1973-)，男，湖南衡阳人，博士，副教授，主要从事复杂气态流场建模与仿真、毒害气体泄漏源搜寻等研究工作。